阅读:0
听报道
等号是数学的基石,数学中的相等(equality)似乎是最没争议的概念。但越来越多的数学家开始认为,等号是数学的原初错误,他们想要用等价(equivalence)的语言重新表述数学,不是关注描述对象的具体方式,而是将对象相互关联的各种不同方式考虑在内。这种关注等价性的数学理论就是所谓的范畴论(category theory)。
数学家 Jacob Lurie 先后写作了944页的《高阶范畴论》和1553页的《高阶代数》来阐述范畴论的思想,这两本程碑式著作的影响被认为堪与格罗滕迪克的代数几何革命相提并论。但新思想的提出也带来了巨大的挑战:数学界要如何吸收这些新知识?当数学被重新书写时,数学家群体要如何应对?知识的真正目的到底是什么?
事实上,范畴论除了作为一种极端抽象的数学理论之外,也已经应用到了物理学领域来描写多体量子纠缠(也就是拓扑序)这种全新的自然现象。在后记中,「返朴」总编文小刚教授、深圳量子科学与工程研究院孔良研究员介绍了数学和物理之间这种深刻的关联,他们认为,这个时代是数学和物理融合的黄金时代。
撰文 | Kevin Hartnett
翻译 | 唐璐
等号是数学的基石。它似乎构成了一个完全基本和无可争议的命题:这些东西是完全一样的。
但越来越多的数学家认为等号是数学的原初错误。他们将其视为一种虚饰,它掩盖了量的相关方式中重要的复杂性——这些复杂性可以揭示大量问题的答案。他们想用等价这种更宽松的语言来重新表述数学。
杜克大学的乔纳森·坎贝尔(Jonathan Campbell)表示:“我们一直用的是相等(equality)的概念,其实应当是等价(equivalence)。”
这些数学家中最杰出的是雅各布·卢里(Jacob Lurie)。今年7月,41岁的卢里离开了他在哈佛大学的终身职位,前往新泽西州普林斯顿高等研究院任教,那里云集了世界上许多最有声望的数学家。
卢里的思想在任何领域都是空前绝后的。他用厚达千页的专业著作,通过超越等号,构建了一个明显不同的方式来理解一些最重要的数学概念。卢里的导师、哈佛大学数学家迈克尔·霍普金斯(Michael Hopkins)说:“我想他认为这才是思考数学的正确方式。”
卢里在2009年出版了他的第一本书《高阶范畴论》(Higher Topos Theory)。这本944页的书就像一本手册,教你如何用新的“无穷范畴(infinity categories)”的语言来解释已经建立起来的数学领域。在那之后的几年里,卢里的思想影响到越来越广泛的数学领域。许多数学家认为它们对数学的未来是不可或缺的。西北大学的约翰·弗朗西斯(John Francis)说:“一旦学会了无穷范畴,就没有人会回头。”

然而,无穷范畴的扩展也揭示出,像数学这样的古老领域一旦试图吸收某个重大的新思想,尤其是当这种思想会挑战其最重要概念的意义时,它将不得不经历成长的痛苦。爱丁堡大学的克拉克·巴维克(Clark Barwick)说:“数学界的保守力量很强。如果不能给出令人信服的理由,就不要指望任何一群数学家会毫不迟疑地迅速接受任何新工具。”
尽管许多数学家已经接受了无穷范畴,但是很少有人完整阅读过卢里高度抽象的长篇专著。因此,一些基于他的思想的工作并不像数学中通常那样严谨。
康奈尔大学数学家茵娜·扎哈里维奇(Inna Zakharevich)说:“我听到人说,‘在卢里的书里讲过。’我说,‘真的吗?你引用的是8000页的文献。这不是引用,这是抱大腿。’”
数学家们仍然在努力理解卢里的思想的重要性和介绍它们的独特方式。他们还在提炼和重新包装他对无穷范畴的表现方式,以便让更多的数学家能理解它们。在某种意义上,他们正在从事任何革命之后必须进行的治理工作,将变革性文本转化为日常法律。通过这样做,他们将数学的未来建立在等价的基础上,而不再是在相等的基础上。
1 等价关系的无穷之塔
数学中的相等似乎是最没争议的概念。两粒珠子加一粒珠子等于三粒珠子。这有什么好讨论的?但最简单的想法也可能是最具欺骗性的。
自19世纪后期以来,数学的基础一直建立在集合上。集合论规定了构造和操作集合的规则或公理。例如,其中有一个公理说的是,你可以将一个包含两个元素的集合添加到一个包含一个元素的集合中,从而产生一个包含三个元素的新集合:2+1=3。
证明两个量相等的形式化做法是将它们配对:将等号右边的一粒珠子与左边的一粒珠子配对。当所有的配对完成后,没有剩余的珠子。
集合论能让人认识到,各有三个元素的两个集合正好能两两配对,但是并不容易察觉到各种不同的配对方式。你可以将右边的第一颗珠子与左边的第一颗珠子配对,或者将右边的第一颗珠子与左边的第二颗珠子配对,以此类推(总共有六种可能的配对方式)。说二加一等于三就忽略了它们相等的所有不同方式。坎贝尔说,“问题是,配对的方式有很多,当我们说相等的时候,我们已经忘了它们。”
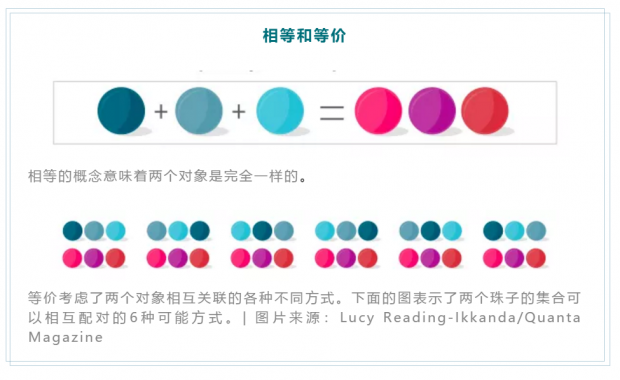
这就是等价出现的地方。相等是一种严格的关系——要么两者相等要么两者不等——而等价则有不同的形式。
当你可以将一个集合中的每个元素与另一个集合中的某个元素完全匹配时,这是一种强等价形式。但比如说,在一个叫做同伦论(homotopy theory)的数学领域,两个形状(或几何空间),如果你在不切割或撕裂它的前提下,可以将一个拉伸或压缩成另一个,则两者是等价的。
从同伦论的角度来看,圆盘和空间中的单点是等价的——你可以把圆盘压缩到单点。然而,将圆盘上的点与单点配对是不可能的。毕竟,圆盘上有无数个点,而单点只是一个点。

自20世纪中期以来,数学家们一直试图发展一种替代集合论的理论,在这种理论中,从等价性的角度来研究数学更为自然。1945年,数学家塞缪尔·艾伦伯格(Samuel Eilenberg)和桑德斯·麦克莱恩(Saunders Mac Lane)引入了一个新的基本对象,这个对象内嵌了等价性。他们称之为范畴。
范畴中可以放入任何东西。你可以有哺乳动物范畴,其中包含世界上所有的有毛发的温血哺乳动物。你也可以构造数学对象范畴:集合、几何空间或者数系。
范畴是有额外元数据的集合,这些额外元数据描述两个对象相互关联的所有方式,包括描述两个对象等价的所有方式。你还可以将范畴视为几何对象,其中每个元素都由一个点表示。
例如,想象一个球面。球面上每个点代表一个不同的三角形。这些点之间的路径表示这些对象之间的等价关系。从范畴论的角度来看,我们不关心描述对象的具体方式,而是关心对象在同类型对象中所处的位置。
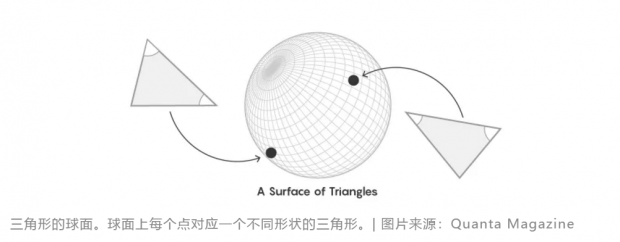
扎哈里维奇说:“有很多我们认为是事物的,实际上是事物之间的关系。‘我的丈夫’这个词,我们把它当作一个对象,但你也可以把它当作我的一种关系。他的某部分是由他和我的关系定义的。”
艾伦伯格和麦克莱恩版本的范畴很适合用于研究强等价形式。但是在20世纪下半叶,数学家们开始越来越多地使用同伦等较弱的等价概念来研究数学。约翰·霍普金斯大学数学家艾米丽·里尔(Emily Riehl)说:“随着数学变得越来越精巧,我们不可避免地会朝这些更精巧的等同概念发展。”在这些更精巧的等价概念中,关于两个对象如何相互关联的信息量急剧增加。艾伦伯格和麦克莱恩的初等范畴无法处理这些。
要了解信息量是如何增加的,先回到表示了许多三角形的球面。如果你可以将一个三角形拉伸或变形成另一个三角形,则两个三角形是同伦等价的。如果有一条路径连接曲面上两点,则两点是同伦等价的。通过研究曲面上点之间的同伦路径,你实际上是在研究这些点所代表的三角形之间的各种关联方式。

但仅仅说两点是由许多等同的路径连接到一起还不够。你还需要考虑所有这些路径之间的等价性。因此,除了要问两点是否等价之外,你还要问,在同一对点上开始和结束的两条路径是否等价——是否有一条路径关联这两条路径。两条路径之间的这条路径的形状为一个盘,盘的边界就是这两条路径。

你可以继续推进。如果两个盘之间有一条路径,那么这两个盘就是等价的,而这条路径的形状将是三维对象。这些三维对象又可能通过四维路径相互关联(两个对象之间的路径总是比对象本身多一个维度)。
最终,你将建立一个等价关系的无穷塔。如果通盘考虑整个塔,你就可以对你所选择的用球面上的点表示的任何对象形成全面的认识。
德州大学奥斯汀分校的大卫·本-兹维(David Ben-Zvi)说:“它只是一个球,但事实证明,要理解球的形状,从某种意义上说,你需要到无穷远处去。”
在20世纪的最后几十年里,许多数学家致力于一个“无穷范畴”理论——这个理论可以研究等价关系的无穷塔。有几个人取得了实质性进展。但只有一个人成功了。
2 重写数学
雅各布·卢里关于无穷范畴理论的第一篇论文并不成功。2003年6月5日,这位25岁的年轻人在科学预印本网站 上发布了一份60页的论文,题为《论无穷范畴》(On Infinity Topoi)。在文中他开始勾勒一些规则,数学家们可以用这些规则研究无穷范畴。
第一篇论文没有得到普遍好评。读完文章后不久,芝加哥大学数学家彼得·梅(Peter May)给卢里的导师迈克尔·霍普金斯发了封电子邮件,说卢里的论文有一些有趣的想法,但感觉很不完善,需要更严格。梅说:“我向迈克尔表达了我们的保留意见,迈克尔转达给了雅各布。”
不清楚卢里是否曾把梅的邮件视为一种挑战,或者他早就计划好了下一步的行动。(卢里多次拒绝了就此事接受采访的请求。)我们只知道,在受到批评后,卢里进入了一个旺盛的多产期,这段时期已经成为传奇。
梅说:“我无法进入雅各布的脑子里,我不能确切地说出他当时在想什么。但毫无疑问,我们批评的文稿与最终版本之间存在巨大差异,后者完全是在更高的数学层面上。”
2006年,卢里在 上 发布了《高阶范畴论》的书稿。在这项里程碑式的成就中,他用一种新的数学基础,基于无穷范畴的基础,建立了取代集合论的机制。伊利诺伊大学厄巴纳-香槟分校数学家查尔斯·瑞泽克(Charles Rezk)做了关于无穷范畴论重要的早期工作,他说:“他用上千页篇幅创造了我们现在都在使用的基础机制。我想我用一辈子都写不出《高阶范畴论》,他用两三年就完成了。”
然后在2011年,卢里又写了一本篇幅更长的专著。在书中,他重新发明了代数。
代数为处理方程式提供了一套优雅的形式规则。数学家们一直使用这些规则来证明新定理。但是代数是在固定不动的等号平衡木上表演体操。如果你去掉这些平衡木,用更精巧的等价概念来代替它们,有些操作就会变得困难得多。
以小学教授的第一条代数规则结合律为例:3个或3个以上数字的和或乘积并不取决于这些数字是如何分组的,比如 2 × (3 × 4) = (2 × 3) × 4。
如果用相等概念,要证明结合律对任何包含3个或3个以上数字的列表都适用是很容易的。但如果使用强等价概念,就会很复杂。如果使用更精巧的等价概念时,即使是像结合律这样的简单规则也会变得非常棘手。
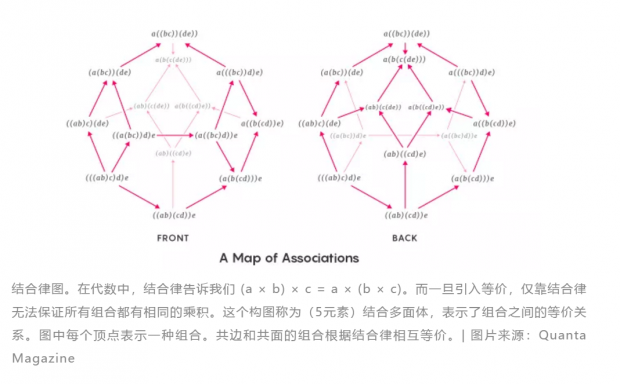
蒙大拿州立大学数学家戴维·阿亚拉(David Ayala)说:“这使问题变得非常复杂,某种程度上使得我们理想的新版本的数学似乎不现实。”
在最新版长达1553页的《高阶代数》(Higher Algebra)中,卢里发展了无穷范畴版本的结合律——以及其他许多代数定理,它们共同奠定了等价数学的基础。
总而言之,他的两本书非常震撼,是引发科学革命的那种著作。里尔说:“规模非常庞大。这个成就可以与格罗滕迪克(Grothendieck)的代数几何革命相提并论。”
然而革命需要时间,正如卢里的书出版后数学家们发现的那样,可能会有很长时间的混乱。
3 消化一头牛
数学家以思维清晰著称:证明是否正确,想法是否有效。但是数学家也是人类,他们对新想法的反应同人类一样:主观、感性、利害取舍。
坎贝尔说:“许多数学读物的基调是,数学家们是在寻找闪闪发光的完美真理。其实不是这样的。他们有自己的品味和觉得舒适的领域,他们会因为审美或个人原因摒弃自己不喜欢的东西。”
从这个角度来说,卢里的工作带来了一个大挑战。甚至可以说是一种挑衅:这里有一种更好的研究数学的方法。对于那些职业生涯中一直致力于研究被卢里的工作超越的方法的数学家们来说,尤其如此。
弗朗西斯说:“这个过程中存在一种紧张,人们并不总是乐于看到下一代重写他们的作品。这一点对无穷范畴论有影响,以前的许多工作都被重写了。”
除此之外,其他一些因素也导致卢里的作品很难消化。长篇大作意味着数学家们需要花费大量时间来阅读。对于处于职业生涯中期的忙碌数学家来说,这几乎是不可能完成的任务,而对于研究生来说,他们只有几年时间来做出能让自己找到工作的成果,因而这也是一个高风险要求。
另外卢里的工作是高度抽象的,即使与高等数学中其他高度抽象的内容相比也是如此。就可接纳程度而言,它并不适合所有人。坎贝尔说:“一些人认为卢里的书是抽象的废话,一些人则甘之如饴,一些人的反应介于两者之间,一些人则是完全不理解。”
科学界一直在吸收新思想,但通常很缓慢,感觉就像一大群人在一起行进。当大的新想法出现时,会对科学界的知识吸收机制构成挑战。坎贝尔说:“一次性导入了太多东西,有点像蟒蛇试图吞下一头牛。有一大团东西正在通过科学界。”
如果你是数学家,认为卢里的方法是解决数学问题的更好方法,那么前进的道路将很孤独。很少有人读过卢里的著作,没有教科书对它进行提炼,也没有研讨会让你明确方向。麻省理工学院的研究生彼得·海恩(Peter Haine)花了一年时间阅读卢里的著作,他说:“让你能真正学会这些东西的方式,就是坐下来自己动手。我认为这是最困难的。不仅仅是坐下来自己动手,而是通过坐下来读800多页的《高阶范畴论》来自己做。”
同许多新发明一样,《高阶范畴论》要求数学家们与驱动理论的机制进行大量互动。这就像要求16岁的孩子先得学会改装引擎才能拿到驾照。与卢里合作的哈佛数学家丹尼斯·盖特格里(Dennis Gaitsgory)说,“如果有一个对驾驶员更友好的版本,就更容易被更广泛的数学观众理解。”
随着人们开始阅读卢里的著作,并在自己的研究中使用无穷范畴,其他问题也出现了。数学家们会用无穷范畴来写论文。期刊审稿人收到这些文章后会说:这是什么?
巴维克说:“在这种情况下,期刊要么反馈荒谬的审稿意见,表现出很深的误解,要么花了几年时间才发表。它会让人不舒服,因为一篇未发表的论文在你的网站上挂了很多年,显得有点滑稽。”
然而,最大的问题不是那些没有发表的论文,而是那些使用了无穷范畴并且确实发表了但是有错误的论文。
卢里的书是关于无穷范畴的唯一权威文献。它们是完全严格的,但是很难完全掌握。尤其不适合作为参考手册——很难查找具体的定理,或者检查在其他论文中可能遇到的无穷范畴的具体应用是否成立。
加拿大蒙特利尔魁北克大学数学家安德烈·乔亚尔(André Joyal)的早期工作在卢里的书中起到了重要作用,他说:“大多数在这个领域工作的人都没有系统阅读过卢里的书。这需要花费大量时间和精力,所以我们只能认为他书中的内容是正确的,因为几乎每次我们检查某些内容时,它都是正确的。事实上,一直如此。”
卢里的书难读也导致后来一些基于这些书的研究不够准确。卢里的书很难读,很难引用,也很难用来核对别人的结果。扎哈里维奇说:“一般的无穷范畴文献给人一种马虎的感觉。”
尽管数学很形式化,但数学并不是只需要只有牧师才能阅读的神圣经文。这个领域既需要小册子,也需要大部头的书籍,除了原初的启示,还需要解释性作品。现在,《无穷范畴论》仍然主要以书架上的大部头的形式存在。
瑞泽克说:“你可以采取‘雅各布告诉了你该做什么,这就够了’的态度。你也可以说,‘我们不知道如何适当地表述这个主题,以便人们可以拿起它并运用它。’”
然而,一些数学家决定迎接挑战,让更多的人在他们的领域里可以把无穷范畴作为一种技术加以应用。
4 对用户友好的理论
为了将无穷范畴转化为可以做真正数学研究的对象,卢里必须证明有关它们的定理。为了做到这一点,他必须选择一个背景来建立这些证明,就像研究几何的人必须选择一个坐标系一样。数学家们称之为选择模型。
卢里在拟范畴(quasi-categories)模型中发展了无穷范畴。其他数学家以前曾经在不同的模型中发展了无穷范畴。尽管这些尝试远没有卢里那么全面,但在某些情况下,它们更容易处理。“雅各布选择了一个模型,并检查了在这个模型中是否一切都成立,但这往往不是最容易的模型,”扎哈里维奇说。
在几何学中,数学家们精确地知道如何在坐标系之间切换。他们还证明了如果定理在一个坐标系中被证明,则它在另一个坐标系中也成立。
对于无穷范畴,没有这样的保证。然而,当数学家们使用无穷范畴撰写论文时,他们往往轻率地在模型之间切换,假设(但不证明)他们的结果可以保持成立。海恩说:“人们不会详细说明他们在做什么,他们会在这些不同的模型之间切换,然后说,‘哦,都是一样的’。但这不是证明。”
在过去六年里,两位数学家一直在努力做出这样的保证。里尔和来自澳大利亚麦觉理大学(Macquarie University)的多米尼克·维里蒂(Dominic Verity)一直在研究一种描述无穷范畴的方法,这种方法超越了以前限定于模型的框架所造成的困难。他们的工作建立在巴维克等人之前的工作的基础上,已经证明了高阶范畴论中的许多定理都是成立的,无论你将它们应用于哪个模型中。他们用一种恰当的方式证明了这种兼容性,里尔解释说:“我们正在研究的无穷范畴,其对象本身就是无穷范畴。范畴论在这里就像在吞食自己。”

里尔和维里蒂还希望以另一种方式推动无穷范畴论的发展。他们阐明了无穷范畴论无论在哪个模型中都成立的那些特性。这种“与模型无关”的表示具有即插即用的特性,他们希望,这种特性能够让那些最初只能通过《高阶范畴论》进入这个领域因而离开的数学家能回到这个领域。
“要进入这个世界,你必须穿过一条护城河,而他们正在放下吊桥。”霍普金斯说道。
里尔和维里蒂希望能在明年完成他们的工作。与此同时,卢里最近开始了一个名为岩豚鼠(Kerodon)的项目,他打算把这个项目作为维基百科式的高阶范畴论教科书。在《高阶范畴论》使等价的数学形式化13年之后,这些倡议是提炼和推广这个思想的新尝试——使等价的数学更加普及。

乔亚尔说:“天才在数学发展中扮演了重要的角色,但实际上知识本身是学术界活动的结果。知识的真正目的是成为社区的知识,而不是一两个人的知识。”
后记
数学和物理融合的黄金时代
撰文 | 文小刚 (麻省理工学院终身教授、格林讲席教授)
物理学的目的是准确地理解和描述各种各样的自然现象。但我们的物理世界是如此丰富多彩,使我们无法用日常生活所发展出来的语言来准确描写这些自然现象。特别是当我们发现一类全新的自然现象时,物理学家常常发现他们需要引入新数学、发明新语言来描写这些自然现象。
像牛顿需要发明微积分来描写他的力学理论所描写的曲线运动。为了描写电磁现象,我们需要用到数学中的纤维丛理论,而为了描写引力现象,我们需要黎曼几何理论。当我们发现微观世界的量子现象后,我们意识到描写我们世界的数学理论并不是微积分、纤维丛和黎曼几何,而是带张量乘法的线性代数。
在凝聚态物理和材料科学中,我们需要理解和描写千千万万、各种各样的物质态。朗道以他深刻的洞察指出,各种各样的物质态其实来源于它们内部各种各样不同的对称性破缺。于是,描写对称性的群论就成为我们描写各种各样物质态的数学语言。
可是过去30年来凝聚态物理的进展揭示了一大类全新物质态的存在。这一类物质态不是起源于对称性,而是起源于材料中的多体量子纠缠。多体量子纠缠(也就是拓扑序)是一种全新的自然现象。我们到底应该用什么样的数学语言才能描写这种全新的自然现象呢?
为了理解和描述多体量子纠缠的内部结构,也就是拓扑序,我们可以考虑这一结构所允许的各种各样的点缺陷,并通过这些缺陷的性质来理解和描述这一结构。但一个拓扑序可以有无穷多个不同的缺陷。为了解决这个无穷大问题,我们可以重新定义什么叫做“相等”:当两个缺陷可以通过局部形变而相互转换时,我们称它们是等价的,或者是“相等”的。我们发现拓扑序中的缺陷只有有限多个等价类。这些不同类型缺陷的等价关系可以是非常复杂的,因为它们包括缺陷之间的融合、编织等等局部操作。描写这些缺陷等价的类的数学理论正是本文所描述的范畴论。范畴论这一极端抽象的数学就这样走进了凝聚态物理。
其实拓扑序中的缺陷不仅可以是点状的,还可以是线状的、面状的等等。描写这些更复杂缺陷的等价类的数学语言就是本文所介绍的高阶范畴学,或无穷范畴学。这些抽象数学理论是描写多体量子纠缠这一全新物理现象的自然语言。新的数学进入物理意味着物理的新革命。现在正是数学和物理高速发展的黄金时期。
撰文 | 孔良(深圳量子科学与工程研究院,南方科技大学)
毫无疑问 Jacob Lurie 的工作值得单独撰文来讨论,但是借这篇文章的东风,加一些简洁的评论也可能是有益的。
Jacob Lurie的两部长篇巨著 Higher Topos Theory 和 Higher Algebra 是近过去20年数学里面最激动人心的进展之一。我们知道微积分和线性代数是现代物理和其他科学的基础语言。粗略地讲,Higher Topos Theory 可以看作是一种新的微积分,而 Higher Algebra 是一种新的线性代数。它们不仅在一个很高的视角上统一了过去的很多数学,而且还提供了一张宏伟的数学新蓝图。而过去已知的数学似乎只是这张新蓝图的一角,可以毫不夸张地说,数学才刚刚开始。
有趣的是,Jacob Lurie 的长文并没有被数学界广泛地接受,除非可以用新语言、新工具来征服传统数学家都攻克不了的老问题 。不过在数学物理学家的圈子里,Jacob Lurie 的贡献不但被广泛而快速地接受,而且已经启发了大量后续和平行的工作。当然这并不奇怪,因为 Lurie 的工作本来就受到了过去30年由弦论和量子场论引发的数学物理新潮流的深刻影响,特别是拓扑场论、mirror symmetry、derived algebraic geometry、En 代数、chiral homology 等等。Lurie 里程碑式的工作一下子在一个很高的高度上,把以前很多零碎的思想统一在一起,并启发了很多全新的问题。
我还想强调的是,即使在 Lurie 的工作之后,量子场论带来的物理直觉仍然是激发想象力的源泉。很多 Lurie 没有问出来的重要问题仍然被不断地挖掘出来。也就是说, Lurie 几千页的浩瀚工程仍然不足以(哪怕是粗略地)描绘数学新蓝图的全貌。大自然给我们的启迪是超越想象力的。
不论如何,我们都会同意,这个时代是数学和物理融合的黄金时代。
对于文中提到的无穷范畴以及 Lurie 工作的意义,哥廷根大学数学教授朱晨畅给出了如下注释:
文中的无穷范畴,也称为(∞, 1)范畴,因为它的高于等于 2 的 morphisms 都是可逆的。在此之前,其他数学家也曾有过不同的模型。不同的很多模型的确是等价的,它们之间的互相比较也有一些早期的工作(例如 Julia E. Bergner 的一篇综述: )。
但 Lurie 工作的意义不仅仅是给了无穷范畴一个更完整的定义体系,而是一种将无穷范畴的思想作为基础,融入当代数学、拓扑、几何(代数几何,这方面也有很多来自欧洲的 Toen 团队的工作),以及代数( Operad 理论)之中的尝试。以志于全面地给数学一个新的,或者说更全面的基础体系。
本文翻译自Quanta Magazine,原文标题为“With Category Theory, Mathematics Escapes From Equality”。点击此处可查阅原文。
版权说明:欢迎个人转发,任何形式的媒体或机构未经授权,不得转载和摘编。转载授权请在「返朴」微信公众号内联系后台。
话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 