在诸多物理学常数中，精细结构常数算是最特殊的一个，历史上也有诸多顶尖物理学家为之痴迷。被誉为“魔数”的它着实拥有与众不同的魅力，它是无量纲的物理常数，其背后的理论本质仍然未知。另一方面，这个从原子光谱的“精细结构”中推导出的数字是描述电磁相互作用的基础，约束着至今仍然牢固的标准模型，却也时常透露着新物理的玄机。因此，尽管这一常数诞生已过百年，探索其奥秘的脚步仍在继续。2020年底，物理学家对精细结构常数的测量又精进一步，为后续更深入的探索指明了方向。

 

撰文 | 一二三

 

2020年12月，物理学家们得到了“魔数”——精细结构常数（符号：α）的最新测量结果：α-1=137.035999206(11)，准确度（Accuracy）达万亿分之81[1]。相比于2018年的结果[2]，这一工作将准确度进一步提升了约2.5倍，成为了目前关于α最准确的测量[3]。新工作一经发表即获得广泛关注，下面先简要介绍精细结构常数，然后更具体地介绍该工作及其意义。

 

什么是精细结构常数？

 

精细结构常数α是一个表征电磁相互作用强度的基本常数，其定义式为

 

 

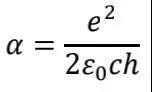
其中e、c、h、ε0分别为基本电荷、光速、普朗克常数和真空介电常数。α取值大约为1/137。作为一个由基本电荷、光速和普朗克常数简单组合构成的无量纲常数，相比于其它有量纲的基本常数，α显得更为特殊。科学家们推测哪怕其数值只是变化一点，比如变为1/138，星球就产生不了碳，人类文明也将无从谈起[4]。为什么α为这般大小？背后有何深意？可以从更基本的原理把它推导出来吗？

 

这些问题可能毫无意义也没有答案，就像在问篮球直径与足球直径的比为何是1.1一样。但物理学家们（至少其中一部分）仍乐此不疲地追问，原因在于，α表述简洁且频繁出现。

 

α的诞生可追溯到1916年，当时德国物理学家索末菲在分析氢原子光谱“精细结构”时为了简化计算，将几个总是以同一形式组合在一起的物理常数（基本电荷、普朗克常数与光速）归并，构成一个新的无量纲常数，即精细结构常数。在物理学中，这三个常数分别代表了电磁相互作用、量子论和相对论[5]，仿佛是大自然在呼唤着人们快来这里一探究竟。而且，人们曾经从类似的追问中获得了更深层次的真理，比如巴尔末对氢原子光谱规律的总结，我们也希望能再次觅得物理世界运行的新规律。后来物理学家果真发现了一些深意，精细结构常数可以作为表征电磁相互作用强度的量——耦合常数（Coupling constant）。

图1：这张费米的著名照片里的精细结构常数公式写反了丨图源：Britannica

 

但目前来看，类似的思考还是带来了许多困惑。泡利曾说：“当我死后，我问魔鬼的第一个问题是：精细结构常数是什么意思。”（也许是一种巧合，泡利生前最后住院的房间号就是137）。有人还给α抹上了一层神秘主义色彩，如英国物理学家爱丁顿认为这个数字具有某种精神内涵，且断言α的倒数应是整数137（此前还坚信过是136），并坚持到了自己生命旅途的终点（当然这已被证明是错误的）。还有一些更为浪漫的说法：当科幻爱好者把数字42当作宇宙的终极答案时，物理学家选择了137，如诺丁汉大学物理学家Laurence Eaves认为，“137这个数字将是人类向外星人发出的信号，表明我们对我们的星球有某种程度的掌握……外星人也知道这个数字，特别是如果他们发展了先进的科学。”遗憾的是这一美妙的说法可能并不成立，2020年4月发表的一项工作中[6]，澳大利亚的一组研究人员宣称，他们对于类星体的观测结果表明精细结构“常数”更有可能是随空间位置而变化的……

 

如此种种，给α披上了一层“神秘”面纱，“魔数”也因此得名。就像费曼所说，“这样一个魔数来到我们身边，却没人能理解它。你也许会说‘上帝之手’写下了这个数字，而我们不知道他是怎样下的笔。”魔数究竟毫无意义还是别有深意？我们不知道。

 

但另一方面，α的实验测量具有重要研究意义。首先它频繁出现在各类原子物理表达式中，如氢原子电离能、原子精细、超精细结构等。它的准确值将关系到相关研究的正确性。更重要的是，α作为耦合常数出现在量子电动力学（QED）和标准模型（SM）中，是检验相关理论正确性的关键。例如，标准模型预言电子反常因数ae可展开成α幂级数：

 

 

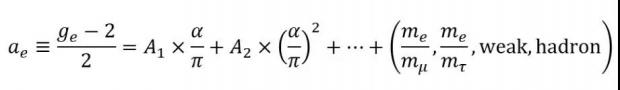
有了不依赖于QED计算的α的准确测量值，可以将其带入(2)右边，与独立方法测得ae进行比对，从而检验QED和标准模型。事实上，正是对α的测量，才证实了μ子和强子对电子反常磁矩有贡献。

 

精细结构常数的最新测量

 

关于α最新的实验结果由法国Kastler Brossel实验室（LKB）的Saïda Guellati-Khélifa研究组完成。他们采用的方法是通过布洛赫振荡（Bloch oscillation, BO），将总量精确可知的光子动量传递给87Rb原子，并利用Ramsey-Bordé原子干涉仪测出原子的反冲速度（Recoil velocity），从而得到普朗克常数与原子质量比h/m，进而得到α。

图2 Saïda Guellati-Khélifa 图源：lkb.upmc.fr

 

原子吸收光子动量后的反冲速度 vr=Nћk/m，其中m为原子质量，N为光子数，ћk为单光子动量。只要实验中能准确知道 N, k，就可以得到 h/m。之后只需利用从氢原子电离能导出的计算α的另一公式

 

 

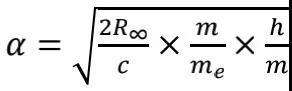
其中里德堡常数R∞和原子-电子质量比m/me已有准确测量值[1]；光速c有规定值，于是就可以得到α。

 

布洛赫振荡（BO）最早在凝聚态物理领域发现，用来描述电子在周期势场中受到一个恒定电场时的行为，后来也被研究光晶格中冷原子物理的科学家们发现并应用。在该实验中，其实现方式是将原子置于两组相向传播的光构成的光晶格中，并使两束光的频率差线性变化。此时原子处在一个加速的驻波场中，感受到一个惯性力从而获得动量。

 

如此传递的动量可以通过布洛赫理论计算周期势场中原子的波函数得到，也可以用原子吸收与发射光子来直观理解：原子吸收沿+n方向传播的光子，获得沿该方向反冲速度；同时通过与反向传播光束间的受激辐射，获得另一份同样沿+n方向且大小相同的反冲速度vr，即一次布洛赫振荡速度变化2vr。采用BO的好处是，能够在短时间内将大量的光子动量传递给原子，提升信号强度；并且通过控制两束激光的频率差能准确知道传递的动量值（N, k）。

 

原子反冲速度由Ramsey-Bordé原子干涉仪探测。干涉仪测量反冲速度的原理可以这样理解：原子物质波与第一束激光脉冲作用时，有一定概率被光子撞击而获得向上的反冲速度，还有一定概率不与光子发生作用。量子世界中这两种情况可以同时发生，原子将处于被撞击与不被撞击的量子叠加态；让原子自由演化一段时间，由于刚才获得速度的不同这时原子物质波将分为量子叠加的上、下两束，且将积累与反冲速度相关的相位差。最终再将这两束重新合并，观察两者间干涉就能确定相位差，从而得到反冲速度。自由演化过程中可通过传递给原子大量动量，例如本工作采用的BO，来增加相位差的积累，从而得到更强的信号。

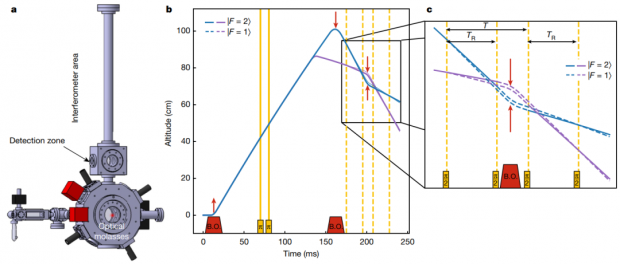
图3：左装置图与实验原理图；两种颜色表示两次实验以抵消重力梯度 | 图源：文献[1]。

 

实验中原子被制备到4μk的极低温度，以便利用物质的波动性及提升测量精度。实验装置及步骤如图3所示，可以只看蓝色轨迹，第一组脉冲将原子分成了相干叠加的上下两束。接下来，BO过程传递给上下两分支一样的动量，但由于空间位置不同，两分支与光相互作用时获得的相位也不一样，且相位差

 

 

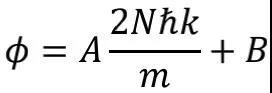
编码了反冲速度的信息。最后只需测量原子在两个能级上的布居数即可测得相位差，从而得到vr，最终得到α。实际上，LKB实验室团队的方法也是2011年[7]、2018年[2]两次测量中（均为当时最准确结果）所采用的。

 

除了测vr，物理学家在数十年来已采用了多种方法来测量α，测量的精度也越来越高，如基于QED理论的兰姆移动测量和电子反常磁矩ae测量，基于量子霍尔效应的测量等。利用BO测量反冲速度vr方案的优势在于，它不依赖于QED计算，提供了一个独立的测量α的方法；并且通过冷原子干涉技术，能够得到较高的测量准确度。

 

另外，基于电子反常磁矩ae推导α的方案也值得一提，通过潘宁阱（Penning trap）中囚禁单电子测得ae。假定标准模型是正确的，通过复杂的QED计算（公式（2））得到α。这一方案得到的最准确 ae=0.00115965218073(28)[8]，α-1=137.0359991496(13)(14)(330)（最大的不确定度由ae测量不确定度导致）[9]。Guellati-Khélifa团队得到的α测量值αLKB2020，结合上述独立给出的ae测量值ae,exp，可以检验标准模型的正确性。最终一如既往地，标准模型又一次经受住了考验。

 

值得注意的是，最新结果与2018年的结果相比，差异达到5.4σ，是实验错误？还是更激动人心的新物理？这些问题仍有待后续研究回答。测量出的新数值也将推动暗物质搜寻、μ子反常因数偏离等基础物理问题的研究[1]。

 

追求极致

 

为了获得如此准确的测量值，需要克服诸多技术上的挑战，要求实验者具备相当的经验，并不断精进实验细节。事实上，Guellati-Khélifa团队在2011年已用同样的方法得到了当时最准确的α测量值。而本次工作的提升在于：好几项系统误差被降低了至少一个量级，例如地球重力场梯度、激光光束准直等；并且对装置做了一定改进，例如真空腔的结构等。正是对于诸如此类细节的孜孜以求，才又一次刷新了α测量的准确度记录，也带领着人们向着真理又迈进了一步。

 

对于精细结构常数的实验测量不仅能加深我们对于基础物理的理解，同时也引领着如今被称为量子精密测量与传感领域的发展。和量子计算、量子通讯等领域一样，该领域旨在运用量子效应提升生产生活方式，而且是几个领域中最有可能在短期内就进入大众生活的。虽然魔数精密测量本身可能对人们影响不大，但测量的工具，例如本实验中用到的原子干涉仪早已被改造成重力仪服务于资源勘探、地震研究等任务。未来，类似的超越传统测量精度极限的研究与应用将不断涌现，量子精密测量大有可为。

 

接下来Guellati-Khélifa和Holger Müller（他领导得到2018年当时最准确的α测量值）团队都将改进实验装置并进行新一轮测量，也许不久后我们就能看到测量值的小数点又往后移动了一位。

Guellati-Khélifa在实验室丨图源：quantamagazine.org

 

在精细结构常数的精密测量这件事情上，Guellati-Khélifa已经坚持了近22年，且仍在不断突破极限。很多人好奇，“什么样的人会为如此细微的提升投入如此巨大的努力？” Guellati-Khélifa提出了三个特点，“必须严谨，富有激情，并且忠于事实。”Holger Müller则表示：“我认为这很激动人心，因为我喜欢搭建闪亮、漂亮的机器。而且也喜欢把它们用到重要的事情中去。”[4]希望就如下面这段话所言：“将小数点往后移一位，你就会发现新的真理。” [10]

 

参考文献与注释：

 

[1] Nature 588, 61–65 (2020)。

 

[2] Science 360, 191–195 (2018)。

 

[3] 参考国际化标准ISO 5725-1和国家标准GB/T 6379，准确度（Accuracy）包含了正确度（Trueness）和精密度（Precession）两方面。

 

[4] https://www.quantamagazine.org/physicists-measure-the-magic-fine-structure-constant-20201202/。

 

[5] 物理学中的“魔数”, 卢昌海 https://www.changhai.org/articles/science/physics/FSC.php#footnotes。

 

[6] Science Advances 6.17 (2020): eaay9672。

 

[7] Phys. Rev. Lett. 106, 080801 (2011)。

 

[8] Phys. Rev. Lett. 100, 120801 (2008)。

 

[9] Atoms 7, 28 (2019)。

 

[10] 出自物理学家叶军，参考https://icqm.pku.edu.cn/rydw/jzyg/236916.htm。