概率论，不只是数学作业中投骰子的问题，而是切实可以预测未来的东西，指导我们应对诸如灾难预警、疾病检测等现实问题——它就是数学家手中的水晶球。本文译自纽约市立大学约克学院数学与计算机系荣誉教授Joseph Malkevitch所撰写Mathematics and Crystal Balls一文，将分为两篇推送。

 

撰文 | Joseph Malkevitch （纽约市立大学约克学院数学与计算机系荣誉教授）

 

编译 | 施昊

 

人们都想希望能够预见未来，比如想知道明天的天气如何；想知道我们是否为自己将来的退休生活储备了足够的积蓄；想知道我们与朋友的友谊将如何发展；或者是知道在大学里学什么课程能够给我们带来快乐。事实上，使用数学工具可能会比用水晶球更有效的预测未来。我们都喜欢岁月安好，并尽可能避免不愉快的时光。然而，人们做的每一件事都可能产生负面结果，因此我们一直在寻找一些方法来规避这些风险。而数学往往能帮助我们。

水晶球丨来源：iStock

 

灾难预测带来的麻烦

 

对于那些想过上“无忧无虑”生活的人来说，很少有地方不会遭受“外界”危险的侵袭。比如说，在美国，一些地区容易遭受龙卷风、大雪侵袭；其他地方有洪灾、飓风，和地震等灾害。在这些由于“大自然的行为”导致受灾的地区，如果我们能够作出灾难预测，使得没有人员伤亡，财产损失降到最小，那就太好了。如今，人们已经开发了一些数学模型以协助处理各类自然灾害。我们所依赖的最常见的预测模型就是越来越准确的一周天气预报。这些预报是科学家基于卫星、陆基监测以及传感器系统的数据给出的。另一方面，这些预测还依赖于以偏微分方程理论和求解这些方程的数值方法为基础建立的大气模型——计算能力和理论的突飞猛进使这些报告更加可靠。

 

一个有趣例子发生在2009年的意大利。一群意大利地质学家和一个政府官员，因被指控未能对2009年意大利拉奎拉地震给出恰当的警告而受到了审判，此次地震造成309人死亡。世界各地的地质学家忧心忡忡，他们理解，尽管在试图预警方面的技术我们取得了很大的进步，但是预测，得到的仅仅是有概率发生而非确定发生。经过审判，7人被判犯有过失杀人罪，处以六年徒刑。让全世界科学家长舒一口气的是，在2014年，上诉法院释放了这些地质学家，并为政府官员减刑。但是那些死者的亲属还是在法庭上谴责政府为自己脱罪的行为。

拉奎拉地震，当地政府办公室也被毁坏丨来源：wiki

 

当一个大风暴来临时，天气预报员如果没能够对潜在危险发出足够严重的警告，他们应该受到指责吗？有时候因为预报原因，可能被大风暴破坏的运输系统被抢先关闭，这会给许多人造成了巨大的后勤和经济问题。如果风暴没有如期而至——这样的事情时有发生，对于许多人来说反而是略有失落的。但反过来说，当人们可能获救的时候，有些人反应不够强烈，这就涉及到“意大利地震”事件中的问题。当然了，与天气预报相比，地震的预测要落后太多了。

 

另一个例子是传染病。有些传染病（例如流感）会每年都会流行，也有周期性的几年流行一次。对于小孩来说，得了百日咳或者麻疹可能会导致死亡；而对于老人来说，他们不知道年轻时接种的一些疫苗还是否有效。此外，如果这时流感出现，老年人可能会受更严重的影响。因为较于年轻人得了流感可能没有大碍，可老人得了流感会导致肺炎或者患上其他危及生命的疾病。那么，父母应该给孩子接种疫苗吗？老人们应该接种流感疫苗吗？

 

虽然一些人有过敏反应，但是从长期的疫苗接种史来看，疫苗极大的延长了人们的寿命，改善了生活的质量。

 

风险行为

 

最近，美国强力球（Power Ball）彩票推出了16亿美元的惊人巨奖！从业者对彩票和赌场赌博有信心的一个重大原因是，数学告诉他们只要有很多的消费者，这些“产业”就会蓬勃发展。如果一个人拥有一个能帮助他选择正确彩票的水晶球，他会赚得盆满钵满。

 

无论是作为个人还是团体的一部分，思考未来时，人们总是对未来抱有期望——有时候是美好的期望，有时候则显得不那么吸引人。对于理解未来能带给我们什么，数学的一个贡献就在于带来了“期望值（expected value）”的概念。当时数学家们使用这一术语时，他们脑中有一个极其精确的定义，但这个定义有许多微妙之处。人们对未来感到紧张的一个原因是他们不确定将来会发生什么。未来涉及随机性和概率（chance，danomness，stochasticness， probability）。为了理解期望值的含义，我们首先要谈一下概率论。

 

我们经常会听到类似如下关于未来的表达：

 

下雨的概率70％；

 

这个地点再次发生地震的概率是一百万分之一；

 

抛一对均匀的骰子，两个骰子的点数之和等于7的可能性是1/6；

 

这种陈述是什么意思呢？要回答这个问题，我们不得不回到数学的两大支柱——基础数学和应用数学。基础数学建立了基于定义和公理（规则系统）的思想和概念体系，然后从这些构造中推导出数学事实和定理。应用数学则采用这些数学并试图用它们来洞察世界。后文我将尝试以相对非正式的方式进行讲述，尽量避免“繁琐”的数学符号和“正式”的定义。

 

首先，概率既适用于有限结果的定义域上，也能被用在无穷的结果的定义域上。为了能够帮助理解这句话，这里有不同的例子来解释。比如有限结果的定义域：

 

苏珊女士想要一对双胞胎，她的孩子出生顺序一共有四种可能——两个男孩先后出生；两个女孩先后出生；先是女孩后是男孩；先是男孩后是女孩。我们只考虑这四种可能顺序。

 

对于无穷的结果定义域，例如，我们可能会捕到一条正在去美国西部某条河流产卵的鲑鱼，并对这条鲑鱼进行称重。称重的可能结果是鲑鱼所能达到的体重范围之间的一个实数——可能是无穷多个重量中的一个。

 

从数学的角度来看，我们能够模拟这些可能性，通过想象从某个“实验”或者实际观察的结果组成集合M。集合M可以是有限的，也可以是无穷的。对于有限结果集合M中的每一个结果m，我们将会分配一个实数给它，称为结果m的概率，记作P(m)。这些实数不能以完全任意的方式分配，它们必须遵循特定的属性或公理：

 

A：P(m)的取值范围在0到1之间，包括0和1。

 

B：所有在M中m对应的P(m)的和，加起来要等于1。

 

请注意，如果m出现的概率是P（m），那么互补事件m’ 的概率，即m将不发生的概率是1-P（m）。也就是说，如果硬币可以是正面或反面，反面的概率是2/5，那么正面的概率是3/5。

 

另外，因为我们只有有限的结果，所以我们不需要任何与极限（微积分）有关的想法来做计算。

 

对于有无穷结果的集合M，我们要求上文列出来的两个条件依旧成立。如果在P(m)中存在最小的值，对于所有的结果而言，他们的概率和就不可能是1了。因为无论多么小的有限数，相加无限次，总会有一个大于1的和。因此，处理无穷集合上的概率有其他的精妙之法。

 

但值得注意的是，我们能够找到一个无穷集合，在这个无穷集合上每个单独事件结果的概率可以是非零的。这是可行的，因为存在无穷的正数数列，数列总和是1。

 

当我们在使用数学时，我们必须将数学概念从一个混沌的、未有定义的术语与公理的世界中抽离，并阐释它们的意义。

 

如果给出一个数据集，比如说30天内你的体重（可能是每天早上同一时间测量的）。人们往往会观察这些数字的波动——这些数大概不会相同。如果你想要了解这些数字的“规律”，一个方法就是去计算一些典型值，如“平均值”，这是一个非常具有吸引力的数。平均值通常是把所有的数值加起来除以试验的次数而得的。

 

使用单个数字来代表一个庞大的数据集的问题在于，表达不同东西的数字集往往会有相同的单个数字作为它们的代表。比如5，5，5，5，5，5的平均值是5，而 -3，-3，-3，13，13，13的平均值也是5。在科学和统计学中使用数字的早期发展之一是，人们认识到，多次“独立”地测量同一数字可能比一次只测量一个数字更可靠。由于测量装置和“人为”过程，无论如何，测量都不可避免地产生一些误差，但是人们可以使测量尽可能可靠。

 

与随机值的均值相似的是一个叫“期望值”的量。假设在某个游戏中，你有3/10的机会赢3美元，7/10的机会赢4美元。通过将结果与结果的概率进行加权，你可以看到如果你玩这样的游戏将会“平均”赢得多少钱。在上述情形下，期望值是你3/10的时间中你会得到3美元，7/10的时间中你会得到4美元，因此

 

期望值= 3(3/10)+ 4(7/10)= (9/10)+ (28/10)= 37/10 = 3.70。

 

如果你需要支付3.75美元才能玩这个游戏，那么平均每玩一次，你就会损失5分钱。在你赢了3美元的时候，你其实损失了75美分；而赢了4美元的时候你才会赚取25美分。但是因为输赢的频率不同，结果的概率不一样，你平均会损失5美分。注意，3.70不是游戏的结果，也不是概率。

 

条件概率

 

有时， “实验”的实施方式会影响事件发生的概率。

 

盒内有两个黑球和两个白球，考虑以下两种不同的方案:：

 

方案A: 搅动盒子，打乱球。从盒子中选择一个球，然后放回第一个球，继续搅动，取出第二个球。

 

方案B: 搅动盒子，打乱球。从盒子里选出第一个球，紧接着选出第二个球。

 

毫无疑问，你拿到两个黑球的概率取决于你用了哪一种方案。在方案B中，如果你第一个抽出来是白球，那根本不可能拿到两个黑球。

 

对于方案A，你只有在第一次抽到黑球，并且第二次抽到的也是黑球时，你才能拿到两个黑球。因此抽到BB(B代表你抽到了黑球)的概率可以通过计算P(BB)=（1/2）（1/2）=1/4。而在方案B中计算抽到两个黑球的概率，我们需要分析情况：

 

第一个抽到的球是黑色，第二球也是黑色。因此第一个球是黑色的可能性是2/4=1/2。现在既然还剩下3个球：两个白球，一个黑球。黑球被抽到的可能性是1/3。考虑到这一点，我们可以看到两个黑色球被抽出的概率是(1/2)(1/3)= 1/6。

 

这个简单的问题与概率论中最基础却又最精妙的问题有关，即条件概率。这个概念可以追溯到研究随机性的最早时期。如果我们用现代符号来表示，P(A|B)表示在B发生的情况下A发生的概率。举个例子，当我们从盒子中取出两个球，给定第一个球是白色的，那么第二个球是黑色的概率就是2/3。我们也可以把P(A|B)看成是P(A∩B)/P(B) = P(第一个球是黑的，第二个球是黑的)/(P(第二个球是黑的)=（1/3）/（1/2）=2/3

 

如何“定义”或考虑P(X|Y)的值？换句话说，我们求的是如果Y发生了后X发生的概率，P(X|Y)是X和Y同时发生的概率除以Y发生的概率。注意，在这个计算中，P(Y)是作为分母的。对于计算P(Y|X)，我们计算Y和X同时发生的概率（与X和Y发生的概率一样），但是我们除以的是P(X)。我们是找“X发生的部分”对“Y和X同时发生的”影响。

 

贝叶斯定理

 

很多人会混淆P(A|B)和P(B|A) 这两个条件概率，它们通常不一样。比如说，如果事件A表示一个药物测试是阳性，事件B表示病人有这种病。那么患上这种病的病人做药物测试是阳性的概率，和做药物测试是阳性的人得这种病的概率，两者是完全不同的。

 

医学检测可能非常准确，但当一种疾病相对罕见时，仅仅因为检测结果是阳性，这并不意味着这个人一定患有这种疾病。一个例子将有助于揭示相关问题。

 

假设一种疾病(D)非常罕见，一般人群发病率0.005，表示1000个人中有5个人患这种病。假设疾病D的诊断测试是验血。当人真患有疾病D时，返回一个患有疾病D指标阳性的概率是0.99。但是不妙的是，当人没有患疾病D时候，检测也可能会出现阳性结果（即患病），概率为0.05，相对较低。注意0.99和0.05不能相加，因为这两个不是互补事件。

 

这里面给出了三个不同的数字，我们将用这些数字通过一些概率的“法则”推导出一些其他数字。让我们引入一些符号来理清思路。符号既有好处也是坏处。这些符号能让人概念更清楚，因为有很多相似但意义不同的概念。为了区分它们，必须用到大量的符号。

 

T表示检测结果为阳性的事件，无论人是否患病；

 

P(D)表示某个人患病的概率；

 

P(T|D)表示一个人在患病时检测为阳性的概率；

 

P(T|D')表示一个人即使没有患病也能检测出阳性的概率；

 

根据以上信息，我们可以写下这三种不同概率的值:

 

P (D) = 0.005

 

P (T | D) = 0.99

 

P(T | D ')= 0.05

 

当检测结果为为阳性时，患者很想知道自己患病的几率，但请注意，答案不是上面给出的数字之一！不过，我们可以通过概率论来推断出这个数字。

 

除了其他的概率工具之外，我们还将利用一个被称为贝叶斯定理或贝叶斯公式的“事实”，这个结果是由托马斯·贝叶斯（Thomas Bayes，1702-1761）提出的，但并未在他生前发表。如今，因为“贝叶斯推理（Bayesian inference）”和“贝叶斯统计（Bayesian statistics）”等术语在统计学上的应用，贝叶斯享有盛名。

托马斯·贝叶斯

 

贝叶斯的得出的结果如下面霓虹所示：

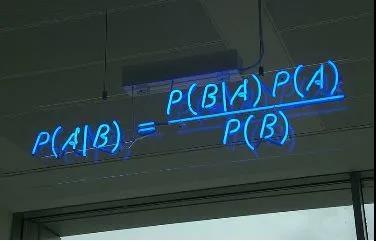
贝叶斯定理丨来源：wiki

 

尽管我们可能只知道P(B|A)，但这个结果允许我们计算与问题P(B|A)相关的其他条件概率。

 

回到上面的诊断情况，让我们看看我们能推断出什么。

 

首先使用补事件的概念，以及事件和补事件的概率之和为1，我们有：

 

P(D') = 1-P(D) = 1-.0005 = 0.995 （某人不会患病的概率）

 

P(T'|D) = 1-P(T|D) = 1-0.99 = 0.01（某人患病但未检测到阳性的概率）

 

P(T'|D') = 1-P(T|D') = 1-0.05 = 0.95（某人没有患病也没有被检测出阳性的概率）

 

现在，让我们看看一些其他值得关注的概率。比如，无论是否患上疾病得到阳性反馈的概率，以及无论患病与否得到阴性反馈的概率。得到阳性反馈的概率有两种方式，一种是患病得到阳性检测结果；另外一种是不患病得到阳性检测结果。我们可以用符号来表示：

 

P(T) = P(T|D)P(D) + P(T|D')P(D') = (0.99)(0.005) + (0.05)(0.995) = 0.00495 +0.04975 = 0.0547

 

P(T ')= P(T ' | D)P(D)+ P(T ' | D ')P(D ')=(0. 01)(0.005)+(0.95)(0.995)=0.9453（这里我们把一个人患病但是没有检测阳性的概率，和没患病也没有检测出阳性的概率相加。）

 

我们需要检查计算的正确性。按理说，0.0547+0.9453加起来应该等于1，而且确实相加等于1！可能这些数字看起有点让人吃惊——得到阳性检测结果的概率相当的小，但这正恰恰反映了很少人患这种疾病。

 

然而，到目前为止，我们还没有得到我们真正感兴趣的数字——如果一个人检测成阳性，那么他患病的可能性是多少？如果一个人被检测成阳性他需要感到很害怕吗？这就是我们需要用到贝叶斯结果的地方。

 

P(D|T) = (P(T|D))(P(D))/P(T) = (0.99)(0.005)/(0.0547) = 0.0904936 ≈0.0905

 

因此，即使测试检测到这种疾病的概率很高，也只有一小部分检测阳性的人确实患病。因为这种病很罕见才导致的这种结果。通常情况下，疑似患者会做另一个独立的测试，看看是否真患病，以免不必要的治疗。

 

贝叶斯的结果也可以用来得到另外三个条件概率，其中两个也可以通过使用“一个事件和它的互补事件的概率和为1”这个事实得到。

 

P(D ' | T)= 0.9095（检测阳性而未患病的概率）

 

P(D ' | T ')= 0.99995（检测阴性而未患病的概率）

 

P(D | T ')= 0.00005（检测阴性而患病的概率）

 

最后这个数字可以用贝叶斯的结果来计算，如下所示:

 

P(D | T ')=(P(T ' | D))(P(D))/ P(T ')= 0.01(0.005)/ 0.9453 = 0.00005

 

是的，尽管这里的符号和计算纷繁复杂，但是这些可以帮助病人和他的医生正确看待罕见病检测中得到阳性结果意味着什么。

 

（未完待续）

 

参考文献

 

[1] Beniston, M,, From Turbulence to Climate: Numerical Investigations of the Atmosphere with a Hierarchy of Models, Springer, Berlin, 1998.

 

[2] Daston, L., Classical Probability During the Enlightenment, Princeton U. Press, Princeton, 1988.

 

[3] Falk, R., and M. Bar-Hillel, Probabilistic dependence between events. The Two-Year College Mathematics Journal. 14 (1983) 240-7.

 

[4] Falk, R., Conditional probabilities: insights and difficulties. In Proceedings of the Second International Conference on Teaching Statistics 1986, pp 292-297.

 

[5] Falk, R., Misconceptions of statistical significance. Journal of structural learning. March, 1986.

 

[6] Gelman, A. and J. Carlin, H. Stern, D. Rubin, Bayesian Data Analysis (2nd edition), Chapman & Hall/CRC, Philadelphia, 2003

 

[7] Hacking, I., The Emergence of Probability, Cambridge U. Press, New York, 2006.

 

[8] Hald, A., A History of Mathematical Statistics from 1750 to 1930, Wiley, New York, 1998.

 

[9] Hald, A., A History of Probability and Statistics and Their Applications Before 1750., Wiley, New York, 2003.

 

[10] Mayo, D., Experimental Knowledge, University of Chicago Press, Chicago, 1996.

 

[11] Mayo, D., Error and Inference: Recent Exchanges on Experimental Reasoning, Reliability, and the Objectivity and Rationality of Science, Cambridge University Press, New York, 2010.

 

[12] Roulstone, I. and J. Norbury, Invisible in the Storm: the role of mathematics in understanding weather, Princeton U. Press, Princeton, 2013.

 

[13] Stigler, S., The History of Statistics: The Measurement of Uncertainty Before 1900, Harvard U. Press, Cambridge, 1990.

 

[14] van Plato, J., Creating Modern Probability: Its Mathematics, Physics and Philosophy in Historical Perspective, Cambridge U. Press, New York, 1994.