一项科学发现常常只能被幸运地发现一次。而牛顿法则一次次被重新推广和修正，每次新发现的结果是，我们原来知道的牛顿法不过是新版的特例而已。其发展和演变历史，正是数学学人不断探索新领域解决新问题过程的写照。牛顿法的奇妙还在于，从诞生以来的一次次发展、推广和创新都是实质性的，而不仅仅是修边角式的改善。

 

撰文 | 曾钟钢（美国东北伊利诺伊大学数学系讲座教授）、丁玖（美国南密西西比大学数学系教授）

 

在《牛顿迭代法传奇（上）：张冠李戴的命名 》中我们说到，科学计算和工程计算上最基本最重要的通用算法“牛顿法”的发明史，是一部诸多大数学家前仆后继的传奇史，从巴比伦-赫伦，到韦达，到牛顿，到拉夫森，到辛普森等等，许多数学家将看似简单的牛顿法不断赋予新的内涵。直至今天，这个传奇仍旧没有结束，本文将剖析牛顿法的基本思想和深层含义，并介绍牛顿法的最新进展。

 

牛顿法的思想

 

在谈论牛顿法扑朔迷离的历史后，我们再次写下本文上篇给出的由辛普森发明的单变量方程牛顿迭代法：

 

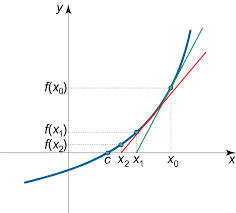
图1：牛顿迭代法图示

 

收敛三要素

 

从这个基本思想出发，我们也很容易看出牛顿法适用的三个条件：

 

 

从上面的分析看出，牛顿法的三个条件极其自然，似乎缺一不可。没有光滑性或局部性，线性近似（3）及迭代收敛就无从说起。没有正则性，那么公式（2）中的逆矩阵就成问题。另一方面，牛顿法的成就又在于，只要这三个条件就足够了。

 

参考文献[1]提到，傅里叶1818 年和柯西 1929 年发表的文章从理论上证明了单变元单个方程牛顿法（1）在三个条件下的二阶收敛性。而现在的共识是牛顿法（2）的最完整的收敛理论归功于前苏联数学家康托若维奇 (Leonid Kantorovich，1912-1986) 发表于1939 年和 1948 年的两篇文章。目前看来，这些文章的收敛性定理表述都有些过于艰涩，其实就是一句话：在上述三个条件下，牛顿法保证二阶收敛。

 

由于康托若维奇完善了收敛理论并把牛顿法进一步应用到无穷维巴拿赫空间，某些文献也把牛顿法称为牛顿-康托若维奇方法。于是牛顿法的冠名争议案子又增加了一个。

 

超定方程组的高斯“救场”

 

包括很多专家在内都有一个流传广泛的误解，以为一个方程组的方程个数必须跟变量个数一样多。这个误解恐怕来自教科书，因为计算数学教科书基本上只谈这类方程组。只有专家读的专著才会谈到，方程个数大于变量个数的方程组称为超定方程组，反之称为欠定方程组。事实上，正方形的方程组虽然有很多理论和求解的方便，但是很多问题本质上就是超定或欠定方程组，在科学计算中根本不可回避。对于超定或欠定非线性方程组，相应的线性近似方程组（4）也是超定或欠定，雅可比矩阵的逆矩阵别说去计算，连定义都没有。怎么办呢？十分遗憾，通用教科书里基本上是找不到答案的。

 

高斯（Johann Carl Friedrich Gauß , 1777-1855）也是无需介绍的伟大数学家。数学史上一个里程碑式的定理叫代数基本定理，也就是说多项式方程必有复数解。历史上众多数学巨匠尝试过证明这个定理，后来发现都差得远呢。这些大师包括达朗贝尔、欧拉、拉格朗日和拉普拉斯，可谓“江山如此多娇，引无数英雄竞折腰”。最终是谁证明了代数基本定理也是个众说纷纭的数学传奇。高斯1799年把这个世纪难题当博士论文做了，一般被认为是第一个正确的证明。高斯尽管在数学上的成就辉煌，最让人津津乐道的故事却是在他七岁上学后的第二年，老师显然是热衷题海战术，让全班练习从1加到100，神童高斯哪里有兴趣去死加一百个数，跟老师说，1+100=2+99=3+98=101， 结果不就是 101×50=5050 吗？他老师是如何吃惊就不难想象了。

 

1809年，“数学王子”高斯第一个将牛顿法推广到超定方程组。在数值求解超定方程组（4）时，雅可比矩阵 J(x0) 不是方阵，而是一个高矩阵，其逆没有定义，当然也就推导不出牛顿法。然而数学王子发现了一个看似不起眼的妙招，当雅可比矩阵是列满秩，即它的秩等于列的个数时，牛顿法可以再度推广到超定方程组：用矩阵的左逆代替传统逆矩阵就行了。

 

要知道常规逆矩阵也自动是左逆，因此辛普森的牛顿法公式 （2）变成了是高斯公式（5）的特例。

 

高斯-牛顿法常常也简称牛顿法。于是牛顿法的适用范围从方形方程组扩展到包括超定方程组。由于超定方程组通常不存在通常意义的解，这种情况下高斯-牛顿法可以求出一个推广意义下的解，称为最小二乘解。这是高斯留给应用数学和计算数学的遗产。可惜它埋没于优化类专业书籍里面，多数计算数学通用教科书上不提。

 

值得一提的是，牛顿法的二阶收敛并不是最快的求根计算方法。比较著名的三阶收敛迭代法有哈雷（Halley）迭代和拉盖尔（Laguerre）迭代，也就是每步迭代获得的精确数位是前一步的三倍。作为课外练习，数学专业本科生都可以构造任何有限阶收敛的快速迭代法。然而从实际计算的角度来看，超过二阶收敛的迭代法仅仅在解决特定问题上可能有些价值。作为通用算法，简单得不能再简单的牛顿法已经二阶收敛，其实际效率在计算中很难被真正超越。哈雷先生虽然以首次算出哈雷彗星轨道周期名垂科学史，但他的迭代法基本上沦落到被遗忘的角落。在此也希望年轻学者不要在研究通用高阶收敛迭代法的问题上浪费时间。除非找到特定应用，超过二阶的收敛速度一般没有实际意义。

 

进一步的探讨

 

一个科学发现常常只能被幸运地发现一次。牛顿法则是一次次被重新推广和修正，每次新发现的结果是，我们原来知道的牛顿法不过是新版的特例而已。

 

从巴比伦-赫伦求平方根扩展到韦达-牛顿-拉夫森的多项式求根， 扩展到辛普森公式求解超越方程和方形方程组，再扩展到高斯求解超定方程组，再扩展到康托若维奇在巴拿赫空间求解，看似简单的“牛顿法”几千年来一再被赋予新的内涵，扩展到更广泛的应用。这期间还引出众多数学大师如傅里叶、柯西和拉格朗日。牛顿法的发展和演变历史，也是数学学人不断探索新领域解决新问题过程的写照。牛顿法的奇妙还在于，从诞生以来一次次的发展、推广和创新都是实质性的，而不仅仅是修边角式的改善。牛顿之后的每次推广都远远超越牛顿的初等方法。当然所有的推广都被习惯性地称为“牛顿法”。于是，“经久不衰的迷思”成为传统。

 

随着电子计算机的出现以及随之而来的计算数学这一学科的诞生，牛顿法作为求解非线性代数方程组的基本通用方法在科学计算的大舞台上大显身手，到处都是其用武之地。由于解方程的问题太常见，对各种迭代法的深入探索和进一步推广从来没有停止过。要想从牛顿法有所创新，三个收敛条件（光滑性、正则性和局部性）是显而易见的入口。

 

光滑性，也就是函数或映射 f 连续二阶可微在绝大多数实际应用中不成问题。对于导数不存在、无法求导或者雅可比矩阵计算成本太高的特定方程，可以使用拟牛顿法和创新不动点迭代。这基本上超出了牛顿法的范畴，在此就不多谈了。无需微分的算法难以利用微积分的线性逼近，因此都未能达到二阶高速收敛而无法成为通用算法。

 

局部性，也就是初始迭代点 x0 取在所求解的一个局部邻域则牛顿法必定收敛。这常常被人误以为是牛顿法的一个弊病。局部收敛的对立面是所谓全局收敛（global convergence），也就是从定义域内的任何初始点出发都保证迭代收敛到一个解。全局收敛算法只存在于求解特定问题的特定迭代。

 

比如说，巴比伦算法在求平方根这个特定问题上就是全局收敛。在发现全局收敛的通用迭代法之前，牛顿法的局部收敛性在一般问题上不输任何算法，所以很难说局部收敛是牛顿法的弊病和短板。局部收敛更恰当的说法是牛顿法的一个特性。由于一般方程组 f(x) = 0 的解可以不唯一，即使找到全局收敛算法，从常理上说这个潜在算法也应该具有局部收敛性，否则无论如何靠近一个解都会跳到另一个解，这算法真能用吗？

 

欣然接受牛顿法的局部收敛特性并加以利用，可以构造出各种全局收敛算法解决特定问题。一个成功的项目始于 1976年，第一篇现代同伦延拓法的文章横空出世，作者之一就是笔者的博士导师李天岩（1945-2020）教授。现代同伦法的进步在于结合微分拓扑和代数几何思想对计算数学领域的渗透。将这些思路与牛顿法相结合，构造出的目前效率最高、速度最快的求解方法和软件适用于多项式方程组。

 

常有人说数学是艺术，意思多半是说数学本身是艺术，看你有没有能力欣赏。读者可能想不到，牛顿法的局部收敛特性还可以用来创作似乎毫不相干的艺术作品。无论是什么世界名画，油画在数学上无非是每个点都有一个颜色，而每个颜色都可以换算成三个数字代表红黄蓝三原色的强度，反之亦然。任何数学方法，只要能给每个点赋予一个或三个数字，这个方法就可以用电脑做出一幅油画，只要发挥想象力创造力，创作可能性是无穷的。

 

图2：分别用复函数 f(x)=sin(cos(x)), sin(x3-1) 和 x(x3-1)2 做出的牛顿油画

 

回到“正则性”

 

至于牛顿法的正则性（regularity）条件，那更是大有文章可做了。

 

用通俗语言说，一个问题是正则的最一般的定义是，这个问题的解的变化上界跟问题数据扰动大小成比例。用数学语言说的话就是，问题的解利普希茨（Lipschitz）连续依赖于数据。

 

正则性是数学上的一个重要性质。在计算数学里更是重要到不可或缺的程度。可以说计算数学只能解决正则问题。非正则的问题又称为奇异（singular）问题。奇异问题跟数值计算水火不容。所以在计算数学教科书上基本上找不到任何奇异问题的数值解法。因为教科书上没说，一个秘密就有点鲜为人知：奇异问题常常可以正则化。至于怎么正则化，那就是施展聪明才智的时候了。寻找正则化方法，探索奇异问题的数值解是计算数学尚未充分开发而又前景广阔的处女地。

 

满足正则性的方程解必定是孤立点。而奇异解可能是孤立的重根，但更常见的情形是方程组的解是个高维流形，比如曲线和曲面，这些都属于所谓非孤立解。非孤立解在科学计算中十分常见。很多应用问题的关键就在奇异点上。回到牛顿-莱布尼茨微积分的基本思路，要求解非线性方程组 f(x) = 0 ，先把方程转换成线性逼近方程（4）。由于雅可比矩阵在解点奇异，不存在逆矩阵。要想扩展牛顿法，可能的突破口就在矩阵求逆。信手拈来有个广义逆矩阵。

 

 

并试图应用于求解奇异方程组。可是问题并不是把求逆上标“-1”换成求广义逆上标“†”这么简单。它需要一大串莫名其妙的条件才能保证收敛，因此难以成为通用算法。

 

直至1982 年，笔者的大师兄朱天照教授首次证明了迭代序列(3)对雅可比矩阵行满秩欠定方程组的局部收敛性。到了九十年代，在香港任教的陈小君和祁力群教授用更广义的所谓“外逆”取代穆尔-彭罗斯广义逆，在某些条件下证明了使用某种特殊外逆的牛顿法二阶收敛到一个驻点，然而不能保证驻点是解。例如，高斯牛顿法（5）形式上是广义牛顿法（6）在超定方程组的特例。而高斯牛顿法（5）收敛到的驻点只能保证满足最小二乘解的必要条件，一般来说不是 f(x) = 0 在通常意义下的解。

 

最新发展

 

问题的瓶颈在哪里呢？广义逆的一个特性是在奇异矩阵附近不连续，稍加扰动矩阵就成为坏条件可逆矩阵，所以在奇异解附近，广义牛顿法（6）退化成辛普森牛顿法（2），直接使用广义逆仅仅是把求解方程的奇异问题换成广义逆矩阵的奇异问题，并没有跳出奇异怪圈。再一个短板在于，正则解只有一种，奇异解的奇妙在于各有各的奇异性。企图一口吃个大胖子，一个方法横扫一切奇异解，天下哪有这种好事。

 

 

 

由于一个偶然的发现，降秩迭代（7）再度推广牛顿法。从巴比伦法、辛普森版本牛顿法、高斯-牛顿法到朱天照公式，前述所有有限维空间中的牛顿法都是（7）的特例。引文[2]中证明，只要映射 f 满足光滑性，所求奇异解满足半正则性和初始点满足局部性三个基本条件，加上投影秩r取为雅可比矩阵在解曲面上的秩，则降秩牛顿法（7）二阶收敛到解曲面上最近的解点。不仅如此，降秩牛顿法（7）成为天然正则化机制。奇异解曲面或曲线之所以奇异，在于经不起折腾。在数据扰动下可以大幅跳跃甚至消失殆尽。然而降秩牛顿法（7）仍然在扰动状态下收敛到一个驻点，这个驻点是消失掉的半正则解点的精确近似而且误差上界跟扰动量成比例，于是半正则的奇异性完全被降秩牛顿迭代清除，完成问题的正则化。这个牛顿法的新发展即将在权威期刊《计算数学》上发表（见文献[2]）。

 

你如果读到这里会问，如果方程组的解奇异程度超过半正则怎么办呢？那么恭喜你。你已经具有数学研究的基本素质。学无止境。学问学问，会问才能有学问。发现问题是解决问题的开始。发现下一个版本求解超奇异方程牛顿法的没准就是你呢。

 

读到这里，你不觉得牛顿法神奇吗？

 

后记：作者以此文纪念我们的导师李天岩教授（1945年6月28日-2020年6月25日）逝世一周年。

 

参考文献

 

[1] T. Yamamoto, “Historical development in convergence analysis for Newton’s and Newton-like methods”, J. Comput. and Appl. Math., 124, 1-23, 2000

 

[2] Z. Zeng，“A Newton’s iteration converges quadratically to nonisolated solutions too，”to appear in Math. Comput.