在凝聚态物理学发展历程中，朗道—金兹堡相变理论奠定了人们对物质形态和有序相及其相变的认识基础，在结合了威尔逊重正化群理论后，形成了朗道—金兹堡—威尔逊范式，并成为整个现代物理学宏伟大厦的重要基石。然而，在复杂电子多体系统的实验研究中，以量子霍尔效应、分数量子霍尔效应和铜氧化物高温超导体的实验发现为代表，涌现了众多超越朗道—金兹堡—威尔逊范式的新奇量子物态，掀开了凝聚态物理学的新篇章。文章从量子霍尔效应出发，介绍了二维电子体系中的几种典型拓扑量子物态。之后，重点介绍二维强关联电子多体系统中的内禀拓扑有序态。围绕Kitaev提出的二维Toric Code量子自旋模型，详细论证了该模型的基态为具有Z2内禀拓扑序的量子自旋液体，讨论了其基态的拓扑简并、低能任意子激发，以及相关的拓扑量子相变。同时，简要介绍了内禀拓扑有序态的最新研究进展和可能的未来发展方向。

 

撰文 | 张广铭、朱国毅（清华大学物理系）

 

来源 | 本文选自《物理》2021年第9期

 

01 朗道相变范式

 

杨振宁先生认为“量子化、对称性与相位因子是20世纪物理学发展的三个主旋律”。菲利普·安德森在20世纪70年代初就指出[1]，多者异也 (More is different) 。当大量粒子相互耦合构成一个多体系统，在低能下它将演生出与原始构成粒子所不同的集体激发准粒子，此为演生现象[2]。比如原子构成晶体，其低能集体激发的准粒子为传播振动与热的声子。然而一旦将晶体拆散分离成原子，声子又不复存焉，所以声子就是一种最为常见而典型的演生准粒子。演生声子这种现象背后的根本原因是：晶体自发破缺了晶体的连续平移对称性，随之催生了无质量的集体激发，这种模式是对有序基态的扰动，反映了一种试图恢复其原始对称性的倾向。事实上，人们在大自然中所观察到的形形色色的物质形态大多是由于其多体系统的自发对称破缺，从而建立起长程有序的物相。

 

所谓“物相”，指的是一个多体系统表现出的集体宏观性质，它不会随着微观参数的微小变动而改变。比如，铁磁体在一定的温度区间内都可以表现出磁性行为，所以叫铁磁相。因此广义而言，物相的定义依赖于某种绝热原理，随着微观参数的变化，只要宏观物理量的各阶导数都连续，没有碰见奇异性，则可判别为同一个物相，并具有定性一致的行为。微观上说，物相的稳定性反映了一种集体秩序。比如，铁磁体中不同原子磁矩由于相互作用倾向于集体同向排列而降低能量，但是热运动又倾向于摧毁这种秩序而形成无序，所以便有了竞争。温度的变化会干预其竞争，比如在高温下热运动导致无序取得胜利，而在低温下相互作用使能量降低则战胜了热运动，于是在两者之间便有了相变。

 

当温度被持续调节到一定程度，达到临界阈值，量变将引起质变，宏观物理量将发生非解析的奇异行为，标志着相变[3]。最早人们在实践经验中发现的是诸如气液转变这样的伴随有潜热等现象的相变，其数学上对应于自由能函数的一阶导数不连续性，被称为一级相变。神奇的是，人们后来发现了气液在更高温度和压强下会变得不可区分，期间经历一个临界点，在临界点上自由能函数的二阶导数不连续性，所以被称为连续相变。宏观上对相变临界点的唯象理解最早由朗道—金兹堡 (Landau—Ginzburg) 的对称破缺理论建立起来：相变的发生是由于自由能随参数的变化导致了某种自发对称破缺。比如低温下原子液体进入超流相，或者金属进入超导相是由于自发破缺了与粒子数守恒相关U(1)规范对称性，从而建立起了宏观的量子相干现象。因此，在朗道—金兹堡的理论中，物相由对称性刻画，而相变由对称性自发破缺导致 (图1)。然而微观上，在参数变动的纤毫之末，一个宏观物理系统中的1023多的粒子是如何相互关联而集体发生改变的呢？此外，更为惊人的是，大自然纷繁复杂的物质体系，其相变却呈现出极其简单的普适行为。后来人们发现这是因为在相变临界点附近微观粒子的关联长度发散，从而系统的宏观性质不依赖于其微观细节，只取决于系统序参量维数和空间维数这样的宏观基本量[3]。

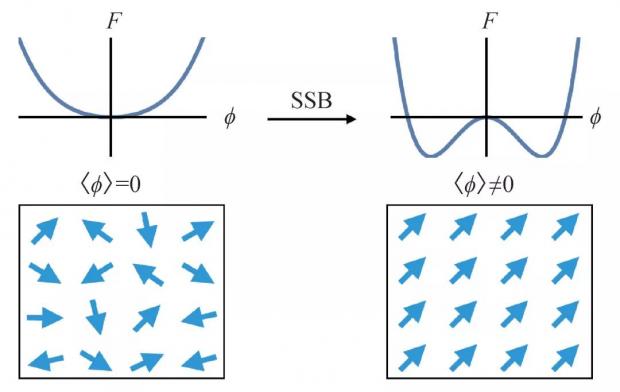
图1 朗道自发对称破缺相变理论的示意图。左侧是无序相，其自由能 F 随着序参量 ϕ 的函数关系如上图所示，自由能极小对应 ϕ=0。典型的例子是铁磁耦合的原子磁矩在高温下由热涨落导致杂乱无序。右侧是有序相，有限序参量才能使得自由能最低，因而基态会发生自发对称破缺， 即spontaneous symmetry breaking (SSB)，磁性系统在低温下原子磁矩同向排列

 

此外，在接近绝对零度时，当改变多粒子系统的某一参数，如粒子间的耦合强度、压力或外加磁场强度，可以将系统从一种无序的状态连续变化到一种有序的状态。由于在临界点附近存在强烈的量子涨落，这类相变与仅由温度所引起的热力学相变完全不同，被称为量子相变[4]，相变的临界点在绝对零度。量子涨落是导致量子相变的根本原因，其来源是量子系统中物理量的非对易性。一个典型的例子是，受横向磁场作用的一维伊辛 (Ising) 模型，随着磁场的增强，该模型会出现从铁磁相到顺磁相的量子相变。这类相变，尽管是发生在绝对零度，但依然可以纳入朗道对称破缺的二级相变理论框架之中。

 

对称破缺相变的微观定量描述由威尔逊(Wilson)所提出的重正化群理论来奠基，其基本思想是考虑热力学 (量子) 涨落，在标度变换下，通过逐级计算短程高能的物理效应来修正微观粒子间的耦合系数，最终得到长波低能极限下的有效物理作用量。由此，描述相与相变的朗道—金兹堡—威尔逊(Landau—Ginzburg—Wilson，LGW)范式犹如一座大厦落成，而对称性也成为凝聚态物理领域研究物相与集体激发行为的主旋律。

 

此外，二维经典物理体系会出现一种特殊的热力学相变，即Kosterlitz—Thouless(KT)相变[5]。根据Mermin—Wagner定理，我们知道在具有连续对称性的二维体系中，热涨落会抵抗连续对称性的自发破缺，摧毁有限温度下的长程序，从而导致有限温度下不可能发生有序相变。然而，在1973年Kosterlitz与Thouless发现，由于经典涡旋拓扑激发的参与，有限温度下可以发生不破缺连续对称性的连续相变。在高温无序相，关联长度有限，关联函数随空间距离指数衰减，而跨越临界点进入低温相之后，关联函数呈现幂律衰减，而且具有普适的标度行为，介于长程序与无序之间，叫准长程有序，其背后的物理图像是系统中的涡旋拓扑激发形成束缚态。作为超越LGW范式的最早例子，这里的涡旋拓扑激发因为相对直观而且最早进入人们的视野，所以早期的凝聚态物理学家还曾将Kosterlitz—Thouless相变温度以下的这个无能隙准长程序称作“拓扑序”，此概念与后来人们所关注的有能隙相中的拓扑序概念不可同日而语。

 

自20世纪80年代开始，人们陆续从实验中发现超越LGW范式的量子多体物质形态。这些物质形态都不具备对称破缺导致的长程序，但是它们之间的转变又不可避免要经历奇异性，亦即发生相变。根据绝热原理，它们应当属于不同的物相。因此，LGW范式预言“沙漠”之中尚有形态各异的“绿洲”。这类超越LGW范式的物相，尽管没有对称性的区分，却有着拓扑性质上的差异[6]。所谓对称性，原来是指系统在某种微观操作下的不变性，比如微观粒子的集体平移、旋转；而所谓拓扑性质，是指系统具有一些离散的整数化的宏观物理量，且这些物理量不随着轻微扰动而改变。比如，常见的一个纽结不随着绳子形变而解开，一个涡旋不随着扰动而消逝，一个甜甜圈一般的圆环面不随着扭捏而化作球面。在量子多体系统中的拓扑往往体现在某种集体激发准粒子波函数的相位因子上，比如在闭合轨迹下积累了不依赖于具体动力学的量子化Berry相位[7]。因此，量子多体系统中演生出来的物相及其相变，继续体现着杨振宁先生曾经所概括的三个主旋律。

 

02 超越朗道范式的拓扑量子物态

 

以二维量子霍尔效应为范例，我们简要回顾拓扑物相的发展，试图勾勒出弱相互作用系统中拓扑电子态的基本物理。在固体材料中，弱相互作用的电子由于量子效应而形成分立的能带结构，从而可以形成绝缘相。在绝缘相中，电子激发态需要克服有限能量，因而在低能下没有电子激发，似乎与真空无异。然而，自从20世纪80年代发现量子霍尔效应以来，人们发现在绝缘体中有一大类特殊的绝缘体，尽管其块体内无低能的电子激发，但是在其边缘上却有不需要克服能量的无能隙激发态，并且还具有强的鲁棒性，其背后的根源正是拓扑相位因子。

 

2.1 量子霍尔效应

 

在磁场中，二维电子气会受到洛伦兹力而围绕磁通发生回旋运动，在能谱上形成朗道能级，其能级间距正比于回旋频率，取决于磁场大小和电子有效质量。每个能级具有与体系尺寸相匹配的巨大简并度，因为在实空间上每个量子磁通就对应于一个电子轨道。由于泡利不相容原理，当电子填满整数个能级的时候，再增加一个电子需要克服系统能隙，所以该体系为“不可压缩”绝缘态。尽管体内激发具有能隙，但在实验上观测到量子化的横向电导表明其系统边缘存在稳健的单向流动的无能隙电子态模式，这就是量子霍尔效应。横向电导的量子化暗示了其内在的拓扑性。在1982年，Thouless，Kohmoto，Nightingale与denNijs四人首次提出了TKNN公式来刻画量子霍尔态的拓扑本质，并且将其体块和边缘的横向电导联系了起来[8]。TKNN公式本质上就是从集体激发的电子波函数中提取出Berry相位。

 

要理解Berry相位通量的量子化，一个最简单而又具有代表性的例子就是考虑一个连续动量空间中的狄拉克(Dirac)旋量波函数，粒子受到磁单极子的作用：

 

其中m代表狄拉克费米子的静质量。如此定义了从二维空间到三维空间的一个曲面映射，直观上相当于将二维动量平面嵌入到三维空间中，或者说把三维中的一个曲面摊开延展到二维平面(图2)。简单分析看到，当m<0，二维动量平面相当于完全包裹了一个磁单极子，从而获得2π的Berry通量。反之，m>0则对应于0通量。通过这个简单而又具有代表性的例子，我们可以窥见，二维封闭流形中的Berry通量量子化本质上是因为三维空间中磁单极子的量子化，对应于二维空间中的一个拓扑结构，称为斯格明子(skyrmion)。

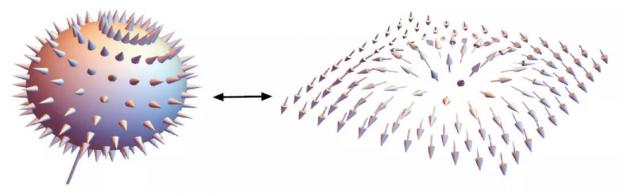
图2 将包裹着一个狄拉克磁单极子的球面延展到一个平直二维平面，即斯格明子(skyrmion)

 

由于拓扑量子数具有鲁棒性，只要系统的能隙不被关闭，则不能发生改变。人们将这样得到的量子数称为拓扑陈数(Chern number)，因为其背后的深刻数学描述是由陈省身先生研究创建的纤维丛理论。由于这样的绝缘体体内具有非零的拓扑陈数，而体外的真空等价于拓扑陈数为零，则其边缘作为两者的过渡区域必然要发生某种特殊的低能物理特征来弥补拓扑数之差，这便是单向传输 (手征性) 的无能隙边缘量子电子态模式。也就是说，边缘模式是由于体内与体外的拓扑差别，因而必然具有鲁棒性，不受边缘形状、杂质散射所影响，而且边缘模式的数目也会由体内的拓扑数完全决定，所以完美解释了实验观测到的量子化横向电导。

 

2.2 量子反常霍尔效应

 

自整数量子霍尔效应从理论上被解释之后，人们很快设想在电子多体系统中，即使在没有外加磁场的情况下也可以发生量子霍尔效应，因而被称为量子反常霍尔效应。1988年，Haldane最先提出了一个理想模型，可以实现量子反常霍尔效应[9]。在一个描述石墨烯低能物理的六角晶格无自旋电子紧束缚模型中，电子只能在近邻格点之间跃迁。由于六角晶格的元胞包含两个格点轨道电子，因此可以在布里渊区 (Brillouin zone，BZ) 中得到两条能带，而两条能带在BZ角点K与-K上发生点接触，形成局部线性色散的狄拉克锥。也就是说，尽管原始构成粒子为非相对论性的紧束缚电子，然而在低能下，该系统中的电子表现为一对具有线性能动量关系的无质量狄拉克费米子 (图3) 。

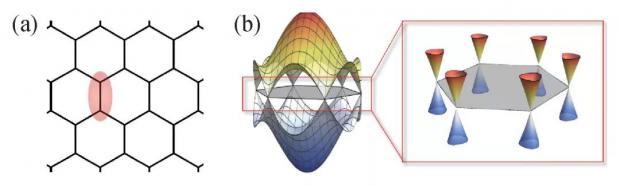
图3 (a)六角晶格；(b)六角晶格最近邻跃迁模型在动量空间中的能带色散关系及其低能狄拉克锥。黑色六边形标记BZ，平均每个BZ分得一对狄拉克锥

 

Haldane在这样的模型中引入一个带相位的次近邻电子跃迁项，使得低能狄拉克费米子获得质量。尤为重要的是，他施加的跃迁相位正好使得两个狄拉克费米子获得相反符号的质量，一正一负。狄拉克费米子获得质量则意味着在能带上打开能隙，可以通过计算拓扑陈数发现，其中一个能带具有+1的陈数而另一个能带的陈数为-1，从而完全填充其中一个能带便可实现量子反常霍尔效应。直观上看，一个带质量的狄拉克费米子可以携带±π的Berry相位通量，而两个组合起来则可以为2π或0两种可能。在Haldane模型里，当取相同的质量则得到0通量，而相反质量则得到2π通量。值得注意的是，这样的模型尽管没有外加磁场，但是依然不可避免地破坏了时间反演对称性。事实上，这是因为电子波函数的相位在时间反演下反号，从而拓扑陈数也继承了这样的行为，非零陈数必然意味着时间反演对称性的破坏。

 

2.3 量子自旋霍尔效应

 

随后人们发现了一个反例，或者说是对原来的拓扑陈数的推广。2004年，C. Kane与E. Mele在Haldane模型的基础上，进一步考虑到自旋轨道耦合效应提出了一个新的理想模型[10]。由于存在电子自旋自由度，他们的模型在低能下本质上相当于将两个Haldane模型，分别对应自旋上和自旋下，以相反的方式来破缺时间反演对称性，从而在整体上维护系统时间反演对称性。然而，只要保证两个自旋自由度不发生耦合散射，则其各自的拓扑数仍然可以良好定义并且满足守恒定律，即自旋自由度为好量子数。更一般而言，该体系只需要时间反演对称性保护，狭义的“拓扑绝缘体”指的就是这样的在时间反演对称性保护下具有非平庸Z2拓扑数的绝缘体。拓扑性质导致在体系边缘上，产生分别对应两种自旋自由度而反向运动的无能隙电子流，从而形成拓扑保护的手征自旋流。换个角度看，其边缘上相当于产生了无质量的自旋轨道锁定的螺旋电子运动模式，这样的拓扑相被人们称为量子自旋霍尔态。后来，与之等价的拓扑相也被张守晟等人预言会在HgTe—CdTe量子阱中实现[11]。自此，拓扑绝缘体受到许多人的关注，并开辟了一个全新的领域。

 

不难发现，由于量子多体系统中还有许多其他的自由度，类似于量子自旋霍尔效应的推广还可以有许多，比如量子能谷霍尔态[12]。除此之外，拓扑绝缘体不限于二维，在三维体系中人们也提出了类似的Z2拓扑数的概念。借助于量子自旋霍尔效应的平台，通过掺入磁性杂质来主动破坏时间反演对称性，薛其坤团队首次观测到了量子反常霍尔效应，从而在实验上首次验证了量子反常霍尔效应[13]。这一大类的拓扑材料由于具有拓扑保护的边缘传输模式，包括电荷、自旋输运模式，乃至能谷输运模式，因而在低功耗自旋、能谷电子学器件应用上具有广阔前景。

 

2.4 二维拓扑超导态

 

 

与常规s波配对超导态不同，p波超导的弱配对BCS极限与强配对BEC极限并不绝热相连，其拓扑不等价性导致必然需要经历一个拓扑相变[14]。考虑 μ > 0 的一个足够大且具有开放边界的系统，由于从系统内部到外面的真空经历了拓扑陈数从 C = 1 到 C = 0 的变化，在系统的边缘上必然要关闭能隙。在开放边界条件下，通过求解Bogoliubov—de Gennes方程得出，在边缘上将出现手征性、单向性准粒子传导，即破坏了时间反演与宇称的马约拉纳(Majorana)费米准粒子模式。

 

更进一步，我们可以求解出，当超导体块中出现了超导涡旋的时候，将会俘获一个严格零能量的孤立马约拉纳费米子。这可以如下简单理解：将超导涡旋近似处理成超导体上一个挖空的圆对称的区域，则围绕其边缘会出现线性色散的手征马约拉纳费米子模式，而由于磁通涡旋的存在抵消掉了p+ip超导自身携带的2π相位环绕。所以，该手征马约拉纳费米子模式波函数满足周期边界条件，从而其轨道角动量整数量子化，其中角动量为0的模式则为严格零能量的马约拉纳费米子。事实上，其零能量受到拓扑保护，在扰动下该结论不变。磁通涡旋与俘获的孤立零能量马约拉纳费米子的复合体被称为马约拉纳零能模式。与单纯的费米子不同，马约拉纳零能模具有非阿贝尔的统计，即两个马约拉纳零能模相互缠绕一周彼此都会获得π相位。如何在实际物理体系中实现p+ip拓扑超导？2008年，傅亮和C. Kane提出在拓扑绝缘体表面态上耦合常规超导体可以实现p+ip拓扑超导[15]，该方案吸引了许多实验学者的关注。其方案的核心是，借助三维拓扑绝缘体表面态上的狄拉克螺旋电子态的强自旋轨道耦合，有效地“冻结”电子自旋自由度，从而演生出p+ip的低能有效配对拓扑超导态。

 

此外，我们简要介绍下一个d+id拓扑超导。其超导配对波函数的轨道角动量 l = 2，具有偶宇称，因而出现在自旋单态配对中。d+id的配对波函数围绕费米面会发生4π的相位环绕，因此得到拓扑陈数C = 2，在边缘上会导致两支手征马约拉纳模式，等价于一支狄拉克费米子模式。此外，考虑到自旋单态配对不破坏SU(2)对称性，所以Bogoliubov准粒子激发携带自旋简并，从而其边缘模式即为一支携带自旋的狄拉克费米子模式。因此，尽管d+id超导也具有非平庸的拓扑，但是其边缘乃至涡旋中心都不具备孤立的马约拉纳模式，从而属于阿贝尔统计类型[14]。有研究者认为在1/4填充附近的石墨烯或者在三角晶格的哈伯德模型中可以实现d+id拓扑超导。

 

2.5 相应的拓扑相变

 

按照绝热原理，有序相的划分依赖于相变，因而有序相与相变犹如一枚硬币的两面不可分割。在传统的LGW范式中，有序相由序参量来刻画，相变则对应于序参量获得一个非零真空期望值，相变理论基本决定于宏观的序参量和空间维数。因而物质的有序相及其相变有一一对应关系，知道了两个相，从对称性和空间维度的信息便基本确定了其间的相变临界理论，这就是凝聚态中的普适类的概念。与传统LGW相变不同，拓扑相变并不涉及对称性破缺，大多由拓扑数来刻画，因而其拓扑陈数的改变则标志着拓扑相变，类比于LGW范式下对称性的改变所描述的相变。在此类拓扑临界点上，往往具有无质量狄拉克色散的费米子激发，其数目取决于两边拓扑相的拓扑数之差，狄拉克费米子质量出现反号，则对应拓扑相变的相变点。比如平庸绝缘态到量子自旋霍尔态的相变，在低能下对应于一个二维螺旋狄拉克费米子从正质量变为负质量[11]。

 

03 超越朗道范式的内禀拓扑有序物态

 

诸如量子霍尔态、量子反常霍尔态和拓扑超导态这样的量子多体纠缠态，由于无法绝热地演变成单粒子直积态，它们的拓扑性质体现在边缘上或者缺陷上的无能隙稳健激发模式，而体内并没有任何不同于平庸相的物理效应。然而，在粒子与粒子的强相互作用下，量子多体系统还可以演生出更加丰富的内禀拓扑有序物态，其拓扑本质则体现在体内可以出现新奇准粒子激发，它们满足的统计性质既非玻色亦非费米统计。

 

3.1 任意子统计

 

通常在三维空间中，点状粒子与粒子之间的任何缠绕轨迹均可以绝热连续收缩回到原点，从而粒子与粒子之间的缠绕必然只能产生0或者2π的统计相位。由于两次粒子交换操作等价于粒子之间的缠绕，所以粒子之间的交换只可能导致其波函数相位改变0或者π，分别对应于玻色子与费米子。然而在二维空间中，粒子之间的缠绕轨迹无法绝热地收缩回到原点，从而原则上可以获得更为一般的Berry相位(图4)。在二维空间中，原则上可以出现超越玻色子与费米子的其他分数化统计相位的粒子，F. Wilczek最早提出[16]，并称之为“任意子”(anyon)。任意子之中又分为阿贝尔任意子与非阿贝尔任意子，前者的相互缠绕只导致波函数整体相位的改变，而后者对应于矩阵形式的相位因子，所以相互缠绕导致波函数被完全改变。任意子在2+1维时空中相互缠绕的世界线等价于数学上的辫子群[17]。

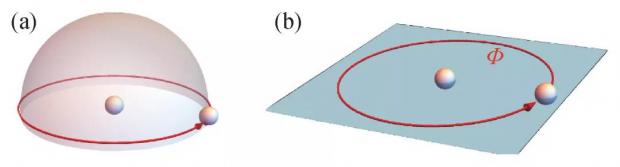
图4 (a)在三维空间中，点粒子之间的缠绕轨迹可以沿着球面绝热收缩回一个点，因而产生的相位只能为0(玻色)或者π(费米)；(b)二维空间中，点粒子之间的缠绕轨迹由于被禁锢在二维平面内而无法绝热地收缩回一个点，因而原则上可以产生任意的Berry相位，包括非阿贝尔类型

 

这些超越玻色与费米统计的任意子便演生于强相互作用的内禀拓扑有序态之中。最为著名的例子便是实验中所观测到的分数量子霍尔态，尽管其微观基本自由度都只是电子，但是其强相互作用的结果导致在低能长波极限下所观测到的准粒子具有分数电荷并满足统计，比如最早观测到的电子比上磁通的填充数 ν = 1/3 的Laughlin霍尔态，其准粒子激发即具有1/3电荷的统计性质，堪称凝聚态中的夸克[18]；而知名的 ν = 5/2 填充的Moore—Read态[19]则具有非阿贝尔的伊辛任意子激发。由于具有有限能隙，分数量子霍尔效应在低能长波极限下的规范涨落可由Chern—Simons拓扑规范理论所描述[20]，所以对应的量子态具有拓扑有序性质。

 

此处的拓扑，本质上是因为系统的低能有效作用量不依赖于时空度规，即在时空坐标变换下作用量保持不变，而表征上体现在这些具有非平庸统计相位的任意子类似于拓扑激发，具有强鲁棒性。同时任意子从产生到湮灭的运动轨迹可以将一个多体基态转变为另一个基态，从而导致依赖于实空间的流形拓扑的基态简并度。任意子的信息完全蕴含在系统基态空间中，可以通过对实空间流形作模变换而提取出任意子的统计相位。比如，将实空间上的一个圆环面作90°旋转的变换，在基态空间中的表示矩阵描述了不同任意子之间相互缠绕的统计相位；而将圆环面剪切开，将其中一个开口自转90°再重新接上这样的变换矩阵则携带了同种任意子之间缠绕的统计相位[21]。有了任意子之间的统计相位信息，便可以通过Verlinde公式计算出任意子的基本融合规则[22]，实现拓扑有序态的完整描述。

 

3.2 量子自旋液体

 

另一个能演生任意子的内禀拓扑物态则是量子自旋液体家族。量子自旋液体的研究可以追溯到阻挫量子磁学以及铜氧化合物高温超导体。30年前，安德森提出共振价键态 (Resonant Valence Bonds，RVB) 的拟设，用来作为阻挫量子磁性基态甚至作为高温超导的母体态[23]。在具有电子半满填充的晶格体系中，由于强库仑相互作用，电子电荷自由度被冻结，只留下自旋自由度，形成强关联莫特绝缘相。在经典理论中，低温下自旋热运动被冻结，自旋倾向于破缺旋转对称性形成某种量子有序态，比如铁磁态和反铁磁态，或者保留自旋旋转对称性而破缺晶格对称性的价键固态：电子两两配对成为价键单态。然而，电子磁矩在反铁磁的超交换作用下，强烈的自旋量子涨落会摧毁任何的有序而恢复高对称性。当存在晶格几何阻挫时，量子涨落的效应尤甚。由于没有破缺任何的自旋旋转对称性和晶格对称性，人们将其喻为“量子自旋液体”。量子自旋液体最有代表性的就是由安德森提出的作为许多不同的价键固态的等权量子叠加的RVB液体态。在该量子态中，电子的自旋和电荷自由度分离而出现分数准粒子激发，演生出的规范场传递粒子间相互作用。在RVB拟设下，自旋子 (spinon) 已然发生配对，而在进行空穴掺杂时，U(1)规范对称性上升为全局对称性，空穴子 (holon) 作为玻色子可以发生玻色凝聚而自发破缺全局的U(1)对称性，这时系统便进入到超导相，这便是高温超导的RVB图像。

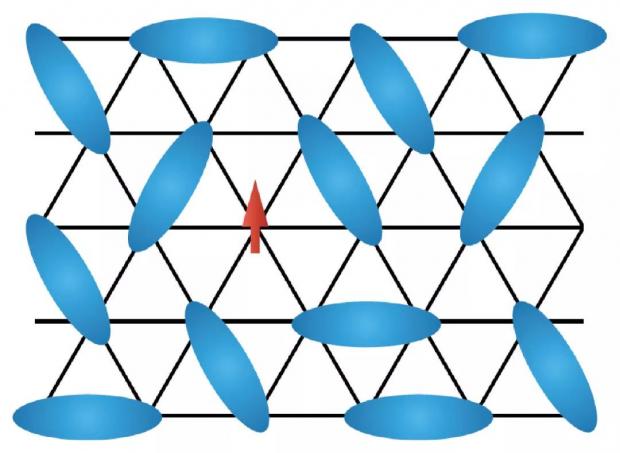
图5 示意最近邻短程共振价键态(RVB)中的其中一个价键态构型。蓝色椭球标记一个由两个格点上的自旋所形成的自旋单态，红色标记一个孤立自旋子(spinon)拓扑激发，其满足费米统计但不携带电荷

 

然而，基于高温超导体系的RVB是由长程的自旋单态组成，其自旋子无能隙而具有费米面，研究起来非常复杂。为此，Rokhsar与Kivelson提出了量子二聚态模型[24]，考虑更原始的短程RVB态中的拓扑激发，用简化的二聚化构型来刻画短程RVB的极限，即退禁闭的自旋子以及演生涡旋规范场，如图5所示。而文小刚则从隶玻色子(slave boson)分解与演生规范场的角度提出了该体系中的Z2拓扑序的概念[25]。随后，Moessner与Sondhi从数值计算上验证了该系统所具有的Z2拓扑序[26]。然而，真正彻底的征服来自1997年Kitaev在arXiv上发布文章所提出的严格可解模型，该模型简单且严格可解，展现出相应的克服能隙的任意子激发与基态拓扑简并[27]。

 

3.3 Z2自旋液体态

 

1997年，A. Kitaev在arXiv上发布一篇名为《藉由任意子实现可容错的量子计算》的文章，首次提出一个名叫Toric Code的自旋模型，名字取义于在圆环面上作量子编码，文章后来正式发表于2003年。该自旋模型严格可解，其基态为量子自旋液体，可以完美地展示Z2内禀拓扑序。该模型十分简约，只保留了最核心的拓扑的信息。与RVB自旋液体不同，此模型并不具有自旋旋转不变性，从而充分展示了Z2量子自旋液体的本质不在于对称性。出于这个模型的极简性与严格可解性，以及Z2内禀拓扑序的基础性，该模型在拓扑序研究领域中的地位堪比伊辛模型在相变研究中的地位，是许多理论和实验研究的一个试金石。

 

Toric Code模型最初定义在一个周期边界条件的正方晶格上，自旋1/2物理自由度处于格点连边上，其哈密顿量表示为

 

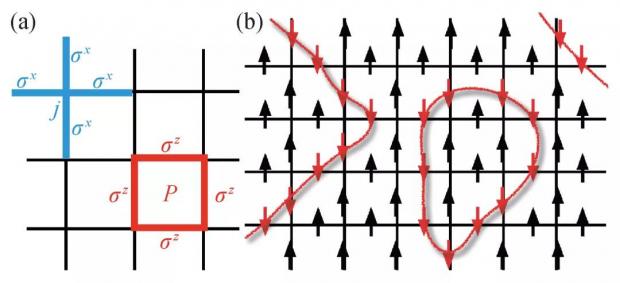
图6 (a)Toric Code 模型中四个自旋乘积形成的相互作用项；(b)Toric Code 模型的基态可以表示为所有闭弦等权相干叠加形成的弦网凝聚态

 

当我们将自旋朝上视作参考真空，而自旋朝下看作弦的一段，那么Toric Code模型的基态可以表示为包含所有闭弦等权重相干叠加态，如图6(b)所示。这种闭弦凝聚态可以看成是传统玻色子凝聚态从点粒子推广到弦这样的延展对象，并且闭弦在基态中可以任意涨落不耗散能量。其实，在经典伊辛统计模型中，高温极限下自旋无序涨落，磁畴壁发生任意的热涨落。如果把闭合畴壁当作基本自由度，该热力学系统则为发生热涨落的各种畴壁。这样的伊辛统计模型与Toric Code模型的基态有着深刻的内在联系。

 

实际上，Toric Code模型等价于一个描述二维空间中最简单的离散化的电磁场理论，其低能激发包含的准粒子有：电荷e、磁通m、马约拉纳费米子f。由于不同格点的σx之间相互对易，所以m粒子相互缠绕的轨迹算符可以等价于一串m闭弦算符作用到基态波函数上，并不出现任何相位，从而m粒子之间具有玻色统计。同理，不同的e粒子相互之间缠绕也不产生相位而同样具有玻色统计。然而，关键的是当一个e粒子环绕一个m粒子一周缠绕时，其运动轨迹涉及一条e弦与一条m弦的相交。由于 σxσz = -σzσx，从而它们之间的交换会贡献一个“-1”，即导致π的Berry相位，如图7所示。也就是说，尽管各自满足玻色子统计，但是e与m粒子相互间却具有非平庸的统计相位π，人称“semion统计”。如此一来，可以简单验证，e粒子与m粒子的复合粒子具有费米统计，记为 f = em。从一个纯粹的玻色自由度的微观模型中，竟然演生出了费米子激发，这不可不谓神奇！如此，我们便确立了该体系中的三种基本低能拓扑激发准粒子e，m，f。广义上说，它们都属于任意子。

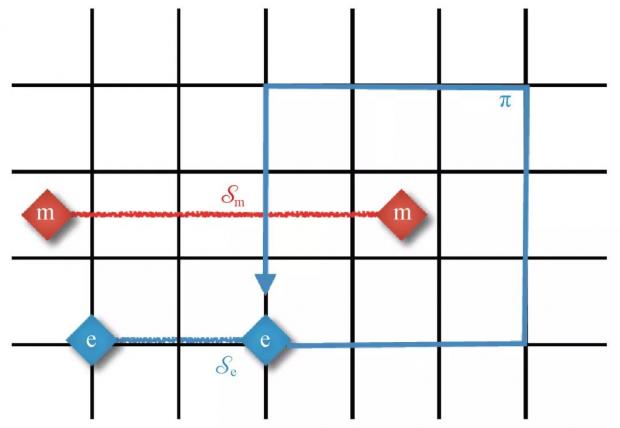
图7 弦算符激发的拓扑粒子及其统计关系。蓝色粗线代表电荷e弦，红色粗线代表磁通m弦，其各自末端为拓扑准粒子。可以验证电荷e弦环绕磁通m弦一圈后，发生Aharonov—Bohm效应导致π相位

 

每一种任意子激发都具有拓扑稳定性，不同的任意子类型只能通过融合来转变，比如e型任意子只能通过与f型任意子融合来得到m型任意子。一般而言，任意子的融合遵循一个简单而基本的代数原则。Toric Code模型任意子的融合原则是

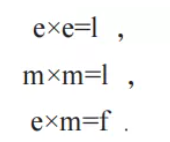
事实上这组融合规则连同任意子的统计定义了一种拓扑序。在三角晶格短程RVB自旋液体中，虽然微观晶格不同，对称性也不一样，但是其中的基本拓扑激发却遵循同样的统计和融合规则，即费米型的自旋子围绕着玻色型的演生规范场vison(π通量涡旋)转一圈会产生π通量激发。所以，三角晶格上的短程RVB自旋液体与Toric Code模型同为一个普适类，称为Z2拓扑有序。之所以称作Z2，是因为其低能激发演生出了Z2规范场。

 

尽管Toric Code模型是在离散的正方晶格上通过自旋模型定义的，但是其封闭弦凝聚的基态图像具有长波极限的特质，因而可以推广到任意的微观晶格。一般性而言，可以完全脱离晶格而通过定义一组连续化的弦构型来构造属于同一个普适类的Z2内禀拓扑序。除此之外，通过定义更丰富代数结构的弦构型，还可以得到更加广泛的弦网凝聚拓扑态。由于弦的非局域特质，这些模型都具有自带拓扑稳定的任意子激发，即内禀拓扑序。事实上，Michael Levin与文小刚在2005年的工作中展示，弦网凝聚图像可以演生出所有的二维非手征的拓扑序[28]。因而，弦网凝聚是一个强有力的物理图像，它从某个角度简明直观地概括了非手征拓扑序的本质属性。

 

事实上，由于基态的局域特征已经被稳定子算符锁死，即局域上不存在开放的e弦或者m弦，所以如果将体系放在一个球面上，则只有唯一基态。尽管很难想象如何将正方晶格放置在球面上，但是闭弦凝聚却可以置于连续空间中，所以可以放置在球面上乃至更一般的拓扑流形上。然而，对于两个方向都为周期性边界条件的正方晶格，相当于将闭弦凝聚体放置在一个圆环面上，这时候环绕两个不可收缩大圆的全局闭弦数目的奇偶性将导致出现四个正交的简并基态。由于局部涨落只能产生可收缩的局部闭弦，全局闭弦可以发生形变或者成对涨落，但是其数目的奇偶性不会改变，因而是一个稳定的全局量子数。不同的基态可以用全局弦算符来转换，也可以用对偶的横向全局弦算符来探测。具体而言，我们可以定义环向 (x方向) 和极向 (y方向) 不可收缩的全局e弦和m弦算符，如图8所示，可以验证除了相互垂直的全局e弦与全局m弦之外，其他的都相互对易。

图8 以两个方向的m弦数目奇偶性来区分的m弦表象的四重简并基态。其中裸的圆环面代表基态，带红圈的表示携带了全局弦算符。环向为x方向，而极向为y方向。对偶变换可以得到e弦表象下的四重简并基态

 

全局的弦算符作用到一个基态上使之变成另一个基态，这从物理图像上说其实就是产生一对任意子激发，并且使之围绕体系大环环游，其后再发生湮灭。由于四重简并基态之间只能通过全局的弦算符来联系，从而局域的微扰需要通过体系尺寸大小级别的巨大微扰才能将一个基态转换到另一个基态，导致两个基态在微扰下能级劈裂随着体系尺寸指数衰减。所以Toric Code模型的简并基态受到拓扑保护，这也正是为何Kitaev提出可以使用这类模型来编码量子信息，从而可以从物理层面上实现容错。

 

此外，弦的量子数只有奇偶守恒，可模2涨落，这其实也是Z2拓扑序内在的Z2对称性的一个体现。事实上，如果将该模型推广到更一般的拓扑流形上面去，比如包含g个亏格的流形，可以形象地理解成具有g个洞的广义面包圈，则按照同样的逻辑可以导致更高的基态简并度4g。也就是说，基态简并度依赖于其所处在的实空间流形的拓扑，从而有所谓“拓扑序”一词。注意到这里的拓扑是实空间的拓扑，跟前面讨论到的动量空间上的涡旋和斯格明子等拓扑结构有本质不同。考虑到该体系具有有限的能隙，从而任意的局域关联函数都是短程关联，具有有限关联长度，那么如此一个“短视”的体系是如何“感知”到流形整体的拓扑的呢？这背后的根本原因在于长程的量子纠缠。量子纠缠是一种量子性的关联，并不能用普通的局域算符的关联函数度量之。

 

另外，在一般微扰下，Toric Code模型其实可以对应一个具有电磁对偶的Z2规范理论，即二维空间中一个最简单的离散版本的电磁理论。其中基本激发粒子正是电荷e、量子磁通m，以及二者复合而成的费米子f。磁通的量子化不禁让人联想起二维超导态。其实Toric Code模型和Z2规范理论正是描述了二维超导态的低能规范动力学行为。通常的量子电动力学中，电子具有U(1)规范对称性，从而电荷数守恒，而其磁通则可以连续变化。在发生安德森—希格斯超导相变之后，U(1)规范对称性下降为Z2，从而电荷数守恒下降为奇偶守恒，相当于把整数的加法运算下降为模2的加法运算。而超导磁通涡旋则被量子化为π通量，库珀对探测到的2π通量相当于单个电子或空穴所探测到的π通量。在常规的s波超导相中，通常考虑的基本低能激发只有马约拉纳费米子。尽管没有外磁场的注入，如果将规范涨落动力学也考虑进来，把系统自身量子涨落产生的超导涡旋看作一种内禀的磁通自由度，则还有马约拉纳费米子与内禀磁通的复合体。可以验证，这正是玻色型的电荷e=mf粒子，见表1。如此一来，Toric Code模型和Z2规范理论并不是十分抽象神秘的理论，而是一个最简单的对偶的电磁理论，描述着凝聚态中熟知的超导相的低能规范涨落的物理。因此，受此启发，Sondhi等人从规范动力学的角度认为超导有序本质上都是超越朗道对称破缺的拓扑有序态[29]。

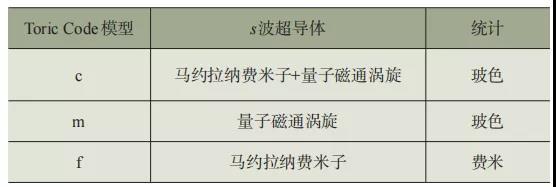
表1 比较Toric Code模型与s波超导相的低能激发

 

3.4 拓扑量子相变

 

Toric Code模型由于其简单性和丰富性在拓扑序的研究中始终处于核心地位，在任何的拓扑物态探索中都充当着试金石的角色。于是，要研究拓扑序的相变，一个很自然的出发点就是研究该Z2内禀拓扑相的相变。一个最简单的考虑就是在Toric Code模型中引入外磁场。事实上，与其等价的规范——希格斯理论，早在1979年已经被Fradkin与Shenker所讨论[30]。尽管Elitzur定理表明，纯粹的规范场其规范对称性不可自发破缺[31]，但是在与之强耦合的物质场诱导下规范场可以发生破缺，即安德森—希格斯机制。当自旋z方向的磁场hz>>1时，该模型确实发生了希格斯相变，拓扑电荷发生凝聚，系统进入希格斯相，在自旋模型上看即为自旋极化的直积平庸相。而在自旋x方向的磁场hx>>1时，Z2规范场的电场线需要克服的能量正比于其长度，从而拓扑电荷被禁闭，这在自旋模型上看也是自旋极化的直积平庸相。希格斯相与Z2电荷禁闭相通过电磁对偶相联系，所以该拓扑相变属于三维伊辛相变的普适类。

 

从拓扑序的角度看，希格斯相变和电荷禁闭相变分别对应于任意子e与m的凝聚，可作为拓扑序之间相变的任意子凝聚机制的一个典范[32]。目前，已知的任意子凝聚主要指的还是具有玻色型自统计的任意子发生凝聚，比如这里的电荷与磁荷。它与常规的玻色凝聚的区别在于，这类玻色子与其他任意子之间由于Aharonov—Bohm相位效应存在非平庸的统计，从而其凝聚会引发其他任意子的禁闭。在Toric Code模型中，由于磁荷m对电荷e来说充当着π通量的角色，所以磁荷的凝聚会导致电荷的禁闭。直观的图像理解是，在磁荷凝聚的基态真空上，磁荷可以任意涨落出现或者消失，而这意味着电荷在真空中游走时会感受到涨落的相位，从而造成干涉相消效应。从逻辑上说，由于电荷在磁荷凝聚的真空中已经不具备良好定义的统计相位，所以不允许独立存在。同理，电荷的凝聚会导致磁荷的禁闭。

 

由电磁对偶相联系的希格斯相与禁闭相，在相图上被Fradkin和Shenker论证可以绝热连接。早在1980年，Jongeward等人通过数值计算发现希格斯相与禁闭相之间的电磁对偶线上，在弱场下出现一级相变线[33]，起始于一个临界点，终结于Z2退禁闭相的边缘，与希格斯相变线和禁闭相变线交汇在一起，疑似出现一个三相变点。30多年以后，在Toric Code模型提出以后，人们从磁场扰动的角度，以探索拓扑相变为动机又对类似相图进行了大量探索。一个重要的工作是，在2010年，Tupitsyn，Kitaev，Prokof′ev与Stamp通过将该模型映射到三维经典伊辛模型，并使用大规模蒙特卡罗数值计算的办法再一次计算了此相图[34]。然而，其数据仍然无法敲定在疑似三相变点的区域上的情况，如图9(a)所示。其中最让人感兴趣的是三相变点的可能，尽管这样的三相变点超越现有的任意子凝聚机制。因为在电磁对偶路径上，从拓扑相出发，如果发生电荷凝聚，则电磁对偶意味着磁荷也同时发生凝聚。然而由于常规的宏观凝聚体是玻色性的，所以Aharonov—Bohm效应会阻止电荷凝聚体与磁荷凝聚体的共存。也就是说，狭义的任意子相变机制无法解释三相变点。因此，尽管围绕该相图已经有了可观的理论与数值的研究，然而在电磁对偶线上的疑似三相变点依旧是未解之谜。自对偶线上的一级相变线和来自希格斯相变与禁闭相变的连续相变线是如何交接？假如是连续的三相变点，那么从拓扑相到非拓扑相的相变机制是什么？任意子命运如何？

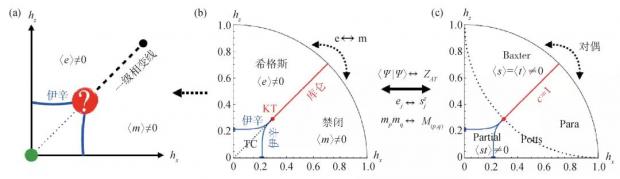
图9 (a)扰动Toric Code模型的全局相图示意。绿点标记无微扰的Toric Code模型的Z2规范退禁闭拓扑相，蓝线标记三维伊辛类的拓扑相变，包括电荷凝聚的希格斯相变和电荷禁闭/磁荷凝聚相变。当电磁对偶时，电荷凝聚相与磁荷凝聚相之间出现一级相变线，它起始于一个临界点上，类似于气液相变，终结于拓扑相边界；(b)从拓扑量子态多体波函数获得的相图；(c)拓扑量子态多体波函数所对应的经典Ashkin—Teller统计模型的相图

 

2019年初，本文作者另辟蹊径，从严格可调节的基态多体波函数的角度，探究了沿着电磁对偶路径上的可能发生的拓扑相变[35]。这类似于Laughlin写下的刻画分数量子霍尔态的多体波函数[18]，只不过我们将其思路推广到含参数调节的波函数来刻画一个拓扑量子相变的过程。同样，类似于Laughlin可将其多体波函数的模方映射到二维经典库仑等离子体问题论述分数霍尔态的性质，我们发现含参数调节的ToricCode波函数的模方也可以映射到经典Ashkin—Teller统计模型。为此，我们借助于张量网络态表象，因为张量网络态可以把一个多体波函数分解为一个个局域的张量的直乘积形式[35]，而局域的张量结构描述的则是物理自由度与某种“纠缠自由度”的耦合。

 

我们在获得了波函数模方的张量网络中，先行将物理自由度缩并掉，而留下“纠缠自由度”，留下的张量网络对应于一个描述局域相互作用的经典统计模型的配分函数[35]。这种引入辅助自由度解除耦合物理自由度，而后求和掉物理自由度而留下辅助自由度的办法，精神上类似于在路径积分上常用的Hubbard—Stratonovich变换。张量网络态的局域性保证了最终得到的经典模型的局域性。借助Ashkin—Teller模型的严格解析解[36]，我们可以确定相变点位置以及任意子关联函数的标度行为，从而准确地描述相变与相变机制。用这套办法我们在调节波函数的路径中重现了电荷凝聚与磁荷凝聚的相变。而在电磁对偶的路径上，惊奇地发现Z2拓扑相经历了一个Kosterlitz—Thouless相变进入无能隙的U(1)库仑气体相：电荷质量随着关联长度发散而逐渐消失，电荷与电荷之间产生与距离成对数依赖关系的二维库仑势[35]。其临界点对应的相变，从库仑势的角度看是配对电荷的安德森—希格斯凝聚相变，本质上即为超导相变。借此我们可以推测，在调节Toric Code模型中外磁场所得到的相图中，沿着电磁对偶路径上的相变类似于禁闭的U(1)规范场到Z2退禁闭规范场的电荷对凝聚相变，相变的普适类与三维的XY模型等价。具体而言，可以用我们严格调节的波函数作为出发点，通过增大张量维数来作为基态拟设，数值求解含有外磁场的Toric Code模型。

 

此外，非阿贝尔拓扑量子有序态被认为可用于实现拓扑量子计算，而斐波那契拓扑量子态则是实现通用拓扑量子计算最为简单的物理系统，相关拓扑相变研究在2020年也获得新进展[37]。利用量子对偶性，我们首先构造了一个含两个互为对偶且可调的斐波那契拓扑量子态的多体波函数。该波函数的模方可以被映射到一个经典统计配分函数上，我们发现对应的统计模型为两个二维耦合的态Potts模型。这是个全新的统计模型，因为它不仅包含了无理数的局域自由度数目，而且还具有非局域的负玻尔兹曼统计因子。此外，通过发展张量网络的特殊技巧，导出了这个斐波那契拓扑态的张量网络态表示。借助于张量网络态的数值计算方法，我们完整而准确地建立斐波那契拓扑物态及其相变的全景相图，并给出多个拓扑量子相变的临界性质[37]。

 

04 结 语

 

值得指出的是，内禀拓扑相的拓扑与此前所介绍的拓扑绝缘体，尽管都统称为“拓扑量子态”，但是有着非常不一样的内涵。拓扑绝缘体或拓扑超导体的拓扑往往跟布洛赫态在动量空间中的Berry相位相关，体现在动量空间中具有相对直观的拓扑结构，比如涡旋或斯格明子。相较而言，内禀拓扑相的拓扑则表观上体现在演生任意子激发在实空间上相互缠绕的Berry相位因子，其相位因子可以推广到非阿贝尔的矩阵形式，其背后的物理根源在于低能演生出的拓扑规范场。Kitaev对于内禀拓扑序是根据其核心物理效应和物理刻画，演生任意子激发定义的[27]。而文小刚则倾向于从微观的绝热原理来分类，只要无法绝热演变成平庸直积态的则定义为拓扑相。在他的理论框架里，拓扑绝缘体和拓扑超导体中的大多数被归类为对称保护拓扑相。只要保护对称性失去，则可以与平庸直积态绝热相连。而像量子霍尔态并不需要对称性保护也无法绝热演变成平庸直积态，但是它们可以通过将两个相反手征性的体系耦合起来变成平庸态，所以叫作“可逆”(invertible)拓扑相。从波函数的角度，文小刚认为不需要对称性保护的内禀拓扑相和“可逆”拓扑相的根源都在于长程量子纠缠，数学上由张量范畴理论所描述[6]。

 

除去分数准粒子激发这样的宏观特征之外，量子自旋液体与分数量子霍尔效应更密切的相关性在于手征自旋液体的提出。最早，Kalmeyer与Laughlin通过对阻挫自旋系统作Holstein—Primakoff变换到玻色子体系，发现阻挫相互作用等价于强磁场，从而将自旋液体跟分数量子霍尔效应从微观上联系了起来，提出了手征自旋液体[38]。最简单的Kalmeyer—Laughlin手征自旋液体可以由阿贝尔Chern—Simons拓扑规范场理论来描述，具有Semion统计的准粒子激发[39]。而具有时间反演对称性的Z2量子自旋液体则需要二分量的相互Chern—Simons作用量，进而描述了两个相互间具有Semion统计的玻色子准粒子激发[29]。

 

目前已知的能够将较多内禀拓扑相联系起来的相变理论框架是任意子凝聚机制[40]。狭义的任意子凝聚机制又叫“拓扑对称性破缺”，是将传统的玻色凝聚建立长程有序的范式推广到具有玻色型自统计的任意子，伴随着这种“玻色子”的凝聚，与之有非平庸统计关系的任意子会被禁闭[32]。一个最简单的例子就是超导涡旋凝聚导致的超导—绝缘体相变[29]。对于更一般的具有非玻色型自统计任意子的凝聚，迄今依旧是极为挑战性的物理问题。

 

纵观凝聚态物理学的发展史，可以发现往往是先从一些具体而又典型的现象个例中获得突破，进而推而广之，建立一整座宏伟大厦，可谓“从一、而二、及三、至无穷”。虽然现实世界是三维空间，然而禁闭在低维空间中的凝聚态物理系统，其涨落效应更强，从而更容易演生出新奇的量子物态。而相比起一维系统，二维量子系统鲜有严格解，却又更容易出现在现实的材料系统中，所以成为强关联多体领域尤受关注而极具挑战的方向。强关联电子系统的典型特征是相互作用与电子动能相比拟，甚至远大于后者，从而能带论完全失效。一般而言，对这样的体系没有普适的严格处理办法，只能通过理论上从不同的角度做近似或者通过大规模数值计算来探知其性质，除了极少数严格可解模型。这样的系统往往具有丰富而新奇的演生量子现象，比如高温超导、分数量子霍尔效应和量子自旋液体，所以是凝聚态物理学领域一个长盛不衰的研究方向。

 

致 谢 衷心感谢于渌先生对本文作者长期从事拓扑量子物态及其相变理论研究的支持和鼓励。

 

参考文献

 

[1] Anderson P W. Science，1972，177：4047

 

[2] 张广铭，于渌. 物理，2010，8：39

 

[3] 于渌，郝柏林，陈晓松. 边缘奇迹：相变和临界现象. 北京：科学出版社，2005

 

[4] Sachdev S. Quantum Phase Transitions. Cambridge University Press，1999

 

[5] Kosterlitz J M，Thouless D J. Journal of Physics C：Solid State Physics，1973，7：1181

 

[6] Wen X G. Rev. Mod. Phys.，2017，89：041004

 

[7] Berry M V. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences，1984，392：45

 

[8] Thouless D J，Kohmoto M，Nightingale M P et al. Phys. Rev. Lett.，1982，49：405

 

[9] Haldane F D M. Phys. Rev. Lett.，1988，61：2015

 

[10] Kane C L，Mele E J. Phys. Rev. Lett.，2005，95：226801

 

[11] Bernevig B A，Hughes T L，Zhang S C. Science，2006，314：1757

 

[12] Ezawa M. Phys. Lett. A，2014，16：1180

 

[13] Chang C Z，Zhang J，Feng X et al. Science，2013，340：167

 

[14] Fu L，Kane C L. Phys. Rev. Lett.，2008，100：096407

 

[15] Read N，Green D. Phys. Rev. B，2000，61：10267

 

[16] Wilczek F. Phys. Rev. Lett.，1982，49：957

 

[17] Nayak C，Simon S H，Stern A et al. Rev. Mod. Phys.，2008，80：1083

 

[18] Laughlin R B. Phys. Rev. Lett.，1983，50：1395

 

[19] Moore G，Read N. Nuclear Physics B，1991，360：362

 

[20] Witten E. Communications in Mathematical Physics，1989，121：351

 

[21] Wen X G. International Journal of Modern Physics B，1990，4：239

 

[22] Verlinde E. Nuclear Physics B，1988，300：360

 

[23] Anderson P W. Science，1987，235：1196

 

[24] Rokhsar D S，Kivelson S A. Phys. Rev. Lett.，1988，61：2376

 

[25] Wen X G. Phys. Rev. B，1991，44：2664

 

[26] Moessner R，Sondhi S L. Phys. Rev. Lett.，2001，86：1881

 

[27] Kitaev A. Annals of Physics，2003，303：2

 

[28] Levin M A，Wen X G. Phys. Rev. B，2005，71：045110

 

[29] Hansson T，Oganesyan V，Sondhi S. Annals of Physics，2004，313：497

 

[30] Fradkin E，Shenker S H. Phys. Rev. D，1979，19：3682

 

[31] Elitzur S. Phys. Rev. D，1975，12：3978

 

[32] Bais F A，Slingerland J K. Phys. Rev. B，2009，79：045316

 

[33] Jongeward G A，Stack J D，Jayaprakash C. Phys. Rev. D，1980，21：3360

 

[34] Tupitsyn I S，Kitaev A，Prokof′ev N V et al. Phys. Rev. B，2010，82：085114

 

[35] Zhu G Y，Zhang G M. Phys. Rev. Lett.，2019，122：176401

 

[36] Baxter R J. Exactly Solved Models in Statistical Mechanics. London：Academic Press，1982

 

[37] Xu W T，Zhang Q，Zhang G M. Phys. Rev. Lett.，2020，124：130603

 

[38] Kalmeyer V，Laughlin R B. Phys. Rev. B，1989，39：11879

 

[39] Wen X G ，Wilczek F，Zee A. Phys. Rev. B，1989，39：11413

 

[40] Burnell F. Annual Review of Condensed Matter Physics，2018， 9：307

 

本文经授权转载自微信公众号“中国物理学会期刊网”。