“暗物质”一直是物理学有待解决的大问题之一。天文学家发现,通过实际观测得到的星系运动速度并不能用常规的动力学理论来解释,需要更多的引力来源,因此提出引入“看不见”的暗物质——这是目前的主流理论。但暗物质现象的解释并非只有这一种,它有一个竞争的科学理论,即修改引力理论(MOND)——通过修改牛顿动力学而不引入暗物质来解释暗物质现象。它是一个优秀的理论吗?它的成功与挑战又在何处?本文将对这一理论进行简要介绍,并与暗物质模型理论进行对比。
撰文 | 陈学雷(中国科学院国家天文台研究员)
在科普讲座或者朋友聚会中,我常常需要向外行的听众朋友们解释“暗物质”的概念。我会告诉他们,现在的天文学家们发现,我们所熟悉的普通物质只占宇宙总密度的大约4.7%,而95%以上的密度则来自暗物质(约25%)和暗能量(约70%)这两种未知成分。经常有人会问出一个厉害的问题:“你说暗物质的证据来自它的引力,有没有可能你们天文学家把引力弄错了?”一些更有怀疑精神的朋友则说,“也许有一天,会发现根本没有什么暗物质,就像没有以太一样。”我觉得这些问题非常好,反映了一种健康的科学怀疑态度。其实,虽然在科普报告或文章中限于时间不一定会提到,但不引入暗物质而试图用新的引力理论解释“暗物质现象”,也是天体物理研究中的一个学派,即所谓修改引力理论学派。
01、暗物质问题
现在所说的暗物质问题最早被发现是在上世纪30年代。当时,在美国加州理工学院工作的天文学家茨维基(Fritz Zwicky,图1)测量了一个星系团中各个星系的运动速度。根据这些速度,我们可以推算需要多强的引力才能束缚住它们;另一方面我们也可以测出星系团内星系的总亮度,再根据恒星的平均亮度推算里面有多少颗恒星,进而根据恒星的质量与光度之比(简称质光比)推算出其质量。结果茨维基发现,星系团中的恒星质量产生的引力不足以束缚住这些星系,需要假定星系团中存在很多不发光的物质,其数量可能是恒星数量的很多倍。茨维基将这些不发光的物质称为暗物质。
在将近40年时间里,茨维基的暗物质假说虽然广为人所知,但并没有引起太多的关注。星系团是宇宙中星系密度很高的地方,宇宙中只有一小部分星系处在星系团内,大部分星系并不处在星系团中,因此这一现象还不是一个普遍现象。天文学家们看到的各种稀奇古怪、难以解释的现象太多了,在对天体没有一个完整可靠的物理图像或模型的情况下,这不过是一个孤立的现象而已。

图1. Fritz Zwicky (左)和他研究的后发(Coma)星系团
但是到了上世纪70年代,人们观测了我们所处的银河系和很多其它星系的旋转曲线——也就是到星系中心不同距离处的恒星或气体的旋转速度值。恒星或气体的旋转速度应该与它们受到的引力有关,星系中心的恒星密度较高,而越到边缘其恒星密度越低,再加上离中心距离更远,因此距离中心越远处受到引力应该越低,那么其旋转速度也应该越慢。但是,实际观测的结果并非如此,星系旋转曲线大多趋于一个常数,这就是所谓的“平坦旋转曲线”(图2)。甚至,人们使用射电望远镜还可以观看星系的中性氢气体的旋转气体,在星系中这些气体的分布范围比恒星所形成的盘要大不少,因此可以看到这些气体所处的边缘已经几乎没有恒星了,而且这些气体本身的量也不多,按理说这里的引力应该下降了,但是这些气体的转速仍然不下降。
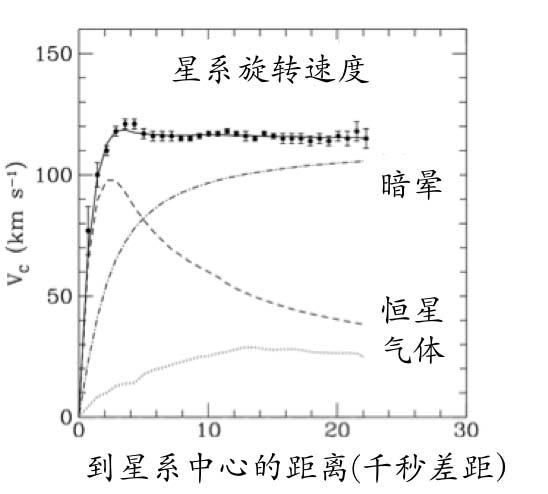
图2. 星系旋转曲线。如果只考虑星系中可见的恒星(虚线)或气体(点线)分布产生的引力,旋转速度将小于观测值,并且会随着到中心距离增大而下降。暗晕、恒星盘和气体合在一起可以解释观测到的旋转曲线。
对于这种现象的一种可能解释就是“暗物质”,一种不发光因而不能被我们看到的物质,假定它们呈球形分布在一个比发光恒星所形成的盘以及气体盘都更大的范围里,构成所谓的暗物质晕(图3)。当我们离开星系中心更远时,那里的引力实际上有很大一部分来自这个暗物质晕,那么在一定范围内,这个引力所导致的旋转速度就不会下降。而为了提供这么大的引力,这些暗晕中的物质总量远多于可见的星系盘。正像任何复杂的科学问题一样,暗物质的观测证据和理论解释也都有很多技术细节问题,引起了许多争论。但到了上世纪80年代初,随着观测方法的改进和数据的累积,证据越来越有说服力,大部分天文学家接受了宇宙中存在大量(远超过可见物质)的暗物质的观念,暗物质模型成为了主流的研究范式。
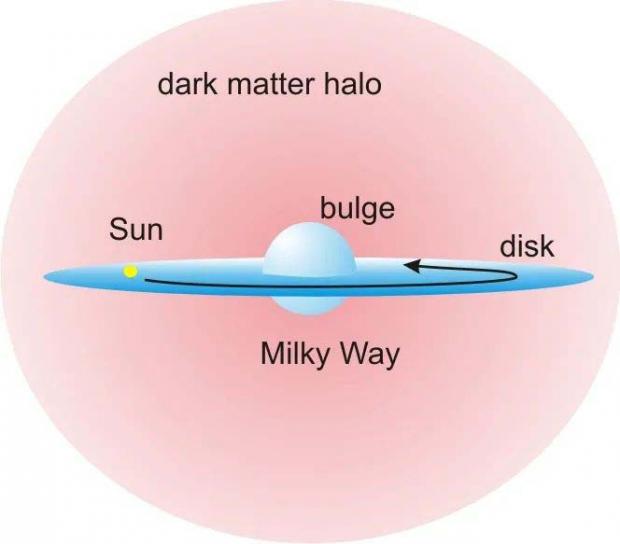
图3. 星系周围暗物质晕示意图
02、修改牛顿动力学
当然,也有人不愿随大流。1980年,一位34岁的以色列物理学家密尔格罗姆(Mordehai Milgrom,图4)利用学术休假到理论物理的圣地——美国普林斯顿高等研究院访问,在此期间他提出了一种新的解释。密尔格罗姆指出,也许,并不存在什么暗物质晕,而是我们习以为常的万有引力定律或运动定律需要修改[1, 2]。

图4. 以色列物理学家Mordehai Milgrom
此前,人们早已普遍接受了牛顿的万有引力定律。爱因斯坦的广义相对论虽然是对牛顿理论的革命,但它与牛顿理论的区别主要是在运动速度接近光速、或者所涉及的尺度接近时空的曲率半径的情况下才明显。对于星系的旋转曲线来说,牛顿和爱因斯坦理论给出的预测差别很小。不过,无论是牛顿理论还是爱因斯坦理论,其直接的检验都是在太阳系尺度上,而在星系尺度上并未有过直接的实验验证,因此不能排除在这一尺度上引力并不符合牛顿或爱因斯坦理论的可能性。
密尔格罗姆提出的模型是一种从经验规律出发的理论。他假定当万有引力的强度(重力加速度的大小)比较大时,物体受到的引力可以用牛顿万有引力的公式描述,但是当其减弱到一定程度时,则偏离标准的牛顿动力学。具体地说,我们所熟悉的物体运动定律是牛顿第二运动定律F=ma,即物体加速度乘以质量等于力。他把这一定律改为
(1) 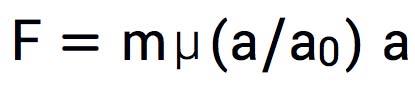
这里a0是一个理论中的新常数,修正因子μ(a/a0)是a/a0的一个函数,满足μ(x>>1)≈1, μ(x<<1)≈x。也就是说,在较大的重力加速度下这个修正因子趋于一个常数,与平常的牛顿定律一致。但当重力加速度减小到一定程度时,加速度与力之间就有一个更复杂的关系。只要满足这个条件,的具体函数形式影响不大,好多不同的取法都能满足要求。当物体远离星系中心时,重力加速度比较小,有了这一修正因子,就可以得到
(2) 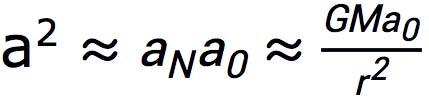
这里aN是按牛顿万有引力公式算出的引力加速度,而a则是米尔格罗姆理论给出的加速度。代入圆周运动的加速度为a = v2/r,就得到
(3) 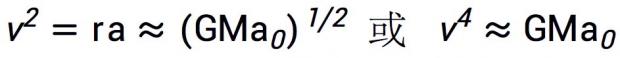
即在远离中心处旋转速度趋于常数。
根据对星系的观测,可得到上式中加速度常数的数值约为a0 ≈1.2×10-8 cm s-2 (a0的值需要根据观测拟合出来,密尔格罗姆最早给出的值为 2×10-8 cm s-2)。这一理论后来一般被称为修改牛顿动力学理论(MOdified Newtonian Dynamics),简称MOND理论。在这一理论中,没有引入暗物质,而是假定普通物质的引力或运动规律与标准理论不同,就能成功地解释星系旋转曲线。至于究竟是物体运动规律(牛顿第二运动定律)、还是万有引力定律(引力大小与距离平方成反比)被修改了,米尔格罗姆认为现在还不能确定,两种可能性都存在。
一个好的科学理论,不仅应该能够解释一种现象,而且最好能用同一理论对多种现象给出解释;不仅应能解释已知的现象,而且最好能预测未知的现象,并得到实验或观测的证实。密尔格罗姆发现,使用MOND理论,不仅可以很好地拟合星系的旋转曲线(预测其值趋近于一个常数),而且可以预测,这个旋转速度曲线最后速度的4次方正比于星系中我们观测到的普通物质的质量。而这一点,也得到了后续观测的很好证实。就在这一时期,天文学家Tully 和Fisher发现,星系的光度与其旋转速度之间存在 L~v4 的关系。如果做出最简单的假定,即星系的光度与其发光物质的质量成正比,那这一关系就完全可以用MOND来解释。相比之下,暗物质模型对Tully-Fisher关系的解释就复杂得多。虽然暗物质模型中,也可以假定星系的一切均受其暗晕质量影响,包括其普通物质的质量、星系的光度和旋转速度都随着暗晕质量增加,因此也能在旋转速度与光度之间找到某种关系,但在最简单的假设下得到的关系是L~v2。而且,在暗物质理论中,这些量之间虽然互相关联,但它们之间并没有严格确定的联系,因此预期这种关系应该有相当大的弥散;而按照MOND理论,这种关系应该是比较精确而没有太大误差的。实测的结果,是这一关系确实比较精确地成立(图5)。
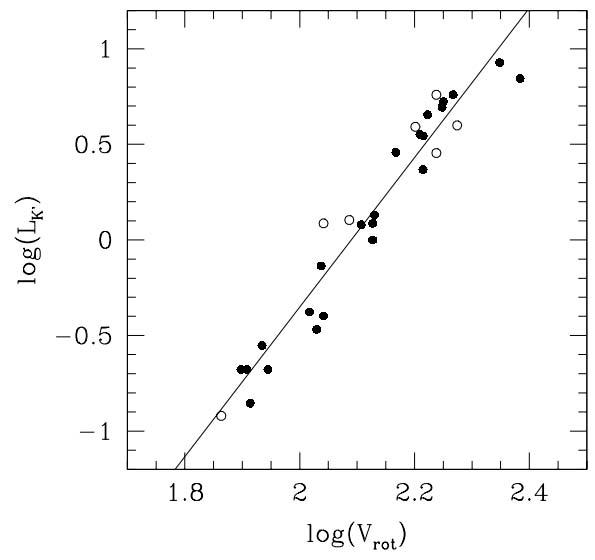
图5. Tully-Fisher 关系 (图取自[3])
03、修改引力理论的自洽性
一个好的科学理论必须自洽,物理学理论必须能对物体在各种情况下的运动给出预测和解释。对于MOND来说,这是一个挑战,因为这个理论是基于经验关系,而不是来自第一性原理,一旦问题超出原来的范围,就不好回答。比如说,上面的理论中只考虑单独一个星系。但是,远处的其它星系会产生如何影响?当然,我们可以做一些简单的假设,比如假定上面公式(2)中的引力加速度a 不是仅仅来自一个星系,而是所有星系引力加速度之和,这样本星系产生的引力加速度最大,并且一般来说其它星系影响并不大,因此不会产生太大的影响(影响较大的情况见后面第5节)。但是,这也只是一种假设而已,还有很多其它可能性。
广义相对论是现代物理学理论的基石,对时空和引力给出了一套自洽且构造严密的完整理论描述,牛顿理论仅是其近似。在广义相对论中,本身已没有牛顿理论中的力了,只有时空的弯曲;物体若不受其它外力,引力作用体现为沿着时空流形的短程线运动。暗物质理论仅仅是引入了一种新的物质成分,并不影响整个时空-引力理论,因此与广义相对论没有矛盾。但MOND理论就不一样了,由于它要求修改引力和动力学理论,因此动摇了整个广义相对论的基础;另一方面,MOND对引力的修改是从一个很特殊的观测现象出发,并没有第一性的原理,所以也很难确定,到底对广义相对论做什么样的修改才能得到这样的理论。因此,很长一段时间里,人们并没有一个相对论性的MOND理论。而这也导致,MOND的理论预言只能局限在星系动力学范围内。对于宇宙演化、光线偏折(引力透镜)、宇宙微波背景辐射等需要相对论理论才能解决的问题,原始的MOND理论无法给出明确的预测。
MOND理论的支持者们当然一直想构建出相对论性的修改引力理论,并做了很多尝试。但直到2002年,另一位以色列物理学家,以提出黑洞熵公式而著称的贝肯斯坦(Jacob Bekenstein)经过多年研究,才构造出了第一种既满足相对论、又能产生MOND行为的理论。在广义相对论中,描写时空弯曲的是所谓度规张量,而在这一理论中,引入了一个新的张量(tensor)场、一个矢量(vector)场、一个标量(scalar)场,以及一个辅助(非动力)标量场,通常的时空度规张量则由这几个量共同决定,因此被简称为张量-矢量-标量(TeVeS)理论[4]。

图6. TeVeS的提出者贝肯斯坦(Jacob Bekenstein)
按照这个理论,一团静态分布的物质可以使粒子具有类似MOND 的动力学行为。但是,这个理论由于引入了多种场,其复杂程度超过一般的暗物质模型,毕竟暗物质一般只要一个场就可以描述了。而且,TeVeS理论也遇到了一些困难,例如它在用于恒星结构时导致不稳定性,在用于预测宇宙结构增长速度时,得到的结果与观测结果不太一致。特别致命的是,2017年,人们探测到了一对中子星并合时产生的引力波。在这次事件(GW170817)发生时人们既测到了引力波信号,又几乎同时探测到了伽马射线信号,二者几乎同时到达,说明引力波的传播速度非常接近光速。而TeVeS预测的引力波传播速度低于光速,因此这一模型现在基本可以被排除了。
不过,虽然TeVeS理论被实验否定了,但这一理论给了人们启发。不久前,两位捷克物理学家 C. Skordis 和T. Złośnik 在分析了TeVeS 失败之处的基础上,又构造了一种新的理论,他们称之为相对论MOND (RMOND) 理论[5, 6]。这一理论中引入了一个具有复杂的相互作用的矢量场和两个辅助标量场。在这一理论中引力波传播速度等于光速。另外很重要的一点是,暗物质理论认为,无论现在还是早期宇宙暗物质都比普通物质多,因此产生的引力效应比单单由普通物质产生的多。而通常的MOND仅在引力加速度弱到一定程度时才起作用,那么在早期宇宙中,由于物质密度比较高,引力加速度也比较大,因此可以推测引力似乎不会被修改,那么这个引力效应就等于普通物质产生的引力,比暗物质模型预测的要低。宇宙早期的声波振荡由引力引起,而这种声波振荡的幅度可以通过观测宇宙微波背景辐射的各向异性测量出来,所以要通过宇宙微波背景辐射观测的检验,RMOND理论还要在早期宇宙里也能产生更强的引力作用,从而使它能替代暗物质模型,给出正确的宇宙微波背景辐射的各向异性,满足现有的各种宇宙学观测。C. Skordis 和T. Złośnik构造的模型做到了这一点,在修改引力的理论上确实是一项重要的成果,也使得MOND的支持者可以声称,他们有一个在各方面都可以和暗物质理论竞争的模型。
04、MOND的挑战:星系团
自其被提出开始,MOND 理论在解释各类星系上都是比较成功的,但是对于星系团MOND却一直不太成功。如果把星系观测中拟合出来的MOND参数用到星系团中,它预测的星系运动速度确实比根据光度测量和牛顿理论得到的数值高一些,但仍比实测的结果低一倍左右。特别是,子弹头星系团(bullet cluster) 是一个不利于MOND理论的例子。
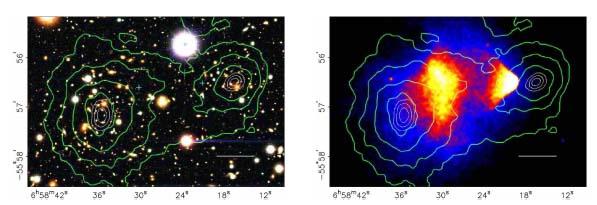
图7:子弹头星系团(bullet cluster)(1E0657-56):左图为光学图象,右图为X-射线图象。曲线表示根据引力透镜效应测出的投影密度分布。
子弹头星系团是两个星系团刚刚发生了高速对头碰撞形成的,如上图所示。星系团内各个星系之间的距离其实很相当大,因此当两个星系团碰撞时,这些星系就像两军对垒时互相射向对方的子弹一样,交错而过,穿到了对方的后面。每个星系团中各个星系之间还分布着许多气体,这些气体互相之间会产生相互作用,无法轻松地相互穿过,而是如同白刃格斗的两军战士一样,撞在一起,并激发出冲击波来。所以,气体分布在靠近整个碰撞残骸的中央,而星系则分布在两侧。星系团中气体温度比较高,会发射X-射线,图中的X-射线就显示了靠近残骸中央、正在向两侧传播的气体冲击波。
如果星系团中分布着暗物质,按照一般的暗物质理论,它们之间的相互作用微弱,因此也会像星系一样相互穿过。实际上按这一理论它们应该和星系没有分离,星系最多的地方也是暗物质最多的地方。由于暗物质占了星系团质量的大部分,因此两边星系最多的地方应该也是引力最强的地方。而按照MOND理论,并不存在暗物质,所有的引力来自普通物质,这既包括星系中的恒星,也包括星系之间的气体。但是在星系团中,星系之间气体的质量比星系中恒星的质量更大,如果没有暗物质而只是有修改引力的话,子弹头星系团中央才应该是物质密度最高、引力最强的地方。那么,如何测量引力呢?人们可以使用引力透镜效应:背景星系的光穿过子弹头星系团时,会被其引力偏折,导致我们看到的星系形状发生变化。虽然我们没有办法知道单个星系原来长什么样子,所以也并不知道单个星系受到的引力透镜效应有多强,但是对临近的很多个星系形状进行平均,就可以知道这一地方引力的强弱。人们在仔细测量了子弹头星系的引力透镜效应后发现,团中引力透镜效应最强的地方是两侧星系最多的地方,而不是中央气体最多的地方。这与暗物质理论相符,而与MOND理论不符[7]。
05、暗星系的挑战
随着观测技术的改进和大规模巡天的进行,天文学家们发现了许多更暗的星系,这些星系提供了新的检验MOND理论和暗物质理论的机会。
对于暗物质模型来说,这些比较暗的矮星系曾经一度构成了比较严重的挑战,被称为“小尺度危机”(small scale crisis)。标准的冷暗物质模型数值模拟预测在大暗晕中应该有许多子暗晕,小星系可以在这样的子暗晕中形成,因此银河系这样的大星系周围应该有成百上千的卫星星系,而当时人们所知道的卫星星系只有二十来个。这就是所谓“丢失的卫星(星系)”(missing satellite)问题[8]。已经发现的卫星星系的质量与理论相比也符合得不好,缺失一些理论预测的大质量卫星星系 (too big to fail problem)。此外,从这些星系的旋转曲线人们可以推测其中暗物质晕的密度是如何分布的。其中许多矮星系在中心都有一个“核”,其内密度基本是常数,而不是像模拟预测的那样,有越接近中心密度越高的“尖峰”,即所谓密度轮廓问题(density profile problem)[9]。
对于这些问题,暗物质研究者有两种解决的思路。一些学者认为,可能暗物质并非之前最为流行的冷暗物质,而是具有某种更为奇特的性质。因此,有温暗物质(warm dark matter)、模糊暗物质(fuzzy dark matter)、相互作用暗物质 (interacting dark matter) 等模型。另一些学者则认为,数值模拟可以很好地预测万有引力的作用,但是对于诸如气体的加热和冷却、恒星形成和反馈等复杂效应,则并不准确。因此,即便理论预测的那些暗物质晕子结构确实存在,但毕竟它们的引力比较小,容易被上面说的这些效应影响,导致其中很多无法形成卫星星系。
近年来的SDSS、Pan-Starr、DES等大规模巡天已发现了不少卫星星系[10],目前总数接近60。而当人们在数值模拟中引入普通物质后,则导致了较少的卫星星系[11]。因此,现有的暗物质理论与观测都还有较大不确定性,对暗物质理论还未构成严重的困难。
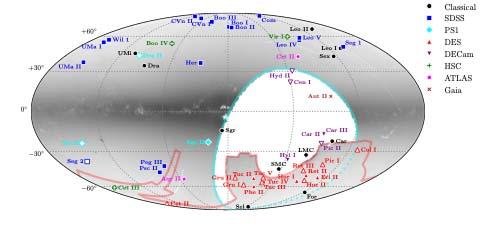
图8.已发现的银河系卫星星系(图中标注了发现该卫星星系的巡天)[10]
MOND理论并不像暗物质理论那样有比较明确的预测。不过,这些新的观测也对MOND给出了新的挑战。特别是,2016年,耶鲁大学的Van Dokkum等人发现了一些面积不小但面亮度却很低的星系,他们称之为超暗星系(ultra faint galaxy)。在测量了这些星系的质量后发现,NGC1052-DF2 和NGC1052-DF4 这两个星系很奇特——它们的质量几乎等于其中发光恒星的质量,也就是说其中并没有暗物质[12]。有趣的是,这两个不含暗物质的特暗星系反倒成了支持暗物质理论、反对MOND的证据:如果引力定律真的需要修改,那么显然在任何星系中我们都会看到引力比牛顿理论预期的更强的现象,也就是星系之中似乎含有暗物质。这两个星系却没有这种迹象,这与MOND的预测不一致,而暗物质理论则可以假设这些星系在之前的某种相互作用中丢失了暗物质晕,从而导致了这一现象。

图9. NGC-1052-DF2 ()
不过,MOND理论的支持者们并未屈服。他们认为,这两个星系之所以没有显示出修改引力的迹象,是因为它们处在大星系的引力场内,附近的大星系产生的引力场强度比较大[13]。我们前面说过,根据MOND理论,只有在引力很微弱的情况下才会显示出与牛顿引力的不同,而当外界产生的引力场比较大时,MOND效应就会被抑制。
实际上,这是MOND理论一个特别之处:它违反了强等效原理——这是广义相对论的基本原理之一。按照强等效原理,在引力场中自由下落的观测者所看到的实验现象并不依赖于周围的环境。而在MOND理论中,即使矮星系在自由下落,周围其它星系产生的引力强弱仍会影响其内部运动规律。很多暗星系和矮星系都会受到近邻星系引力场的影响。如果确如MOND理论所预测的,那么应该可以看到其中受外界引力影响较大的,偏离牛顿引力较小。目前,人们正在利用观测数据对此进行检验。从目前的初步结果看,似乎MOND理论在这方面并不太成功[14]。不过,超暗星系的观测目前还比较少,这方面的研究刚刚开始,恐怕还需要过一段时间才能得出结论。
06、结论
总的说来,目前暗物质理论和MOND理论仍是一对竞争的科学理论。暗物质理论能够更容易地纳入现有的物理学框架,并且基于暗物质理论,可以对星系、星系团、大尺度结构增长、引力透镜、宇宙微波背景辐射等许多观测给出定量化的理论预测。总体来说这些预测与观测也符合得比较好,因此暗物质理论目前还是更受到大部分研究者的青睐而成为主流的理论。不过,自上世纪80年代以来,人们进行了许多暗物质探测实验,但迄今还未能探测到暗物质,因此暗物质理论还不能说已取得胜利。
MOND更像是一个经验模型,不容易纳入现有的物理学框架,相对论性的MOND理论都非常复杂,几个早期的模型如TeVeS和STVG已被引力波速度测量结果排除。不过,正如新出的RMOND模型所显示的,还是有可能构造出满足现有观测的模型。因此,MOND虽然目前不是主流,但仍不失为一种有竞争力的、值得继续研究的候选模型。这一理论也有不少坚定的支持者。在星系尺度上,总体来说MOND与观测符合得不错,在解释Tully-Fisher 关系等方面,甚至可能还有优于暗物质模型之处,但是在星系团尺度上表现不佳,还面临子弹头星系团的挑战。近期发现的一些暗星系也对MOND理论构成了新的挑战。
一些MOND 研究者似乎主观上总是感到他们受到了“主流”的打压或忽视。我不知道这种感受在多大程度上反映了客观真实。我觉得可能是“情人眼里出西施”,一些MOND研究者似乎真诚地相信自己的理论有很强的证据,而看不到其中的弱点,因而别人若没有被说服,就总觉得是别人心存偏见。比如,最近支持MOND的美国天文学家David Merritt写了一本书A Philosophical Approach to MOND(《MOND的哲学处理》)[15],旁征博引了波普耳、拉卡托斯、费耶阿本德等科学哲学家的理论,认为依照各种判据,MOND都胜过暗物质理论。但是,这里的争议问题并不在于各种不同的哲学判据,而在于他单纯强调了对MOND有利的证据,例如MOND对Tully-Fisher关系的成功预测,可是对于MOND在星系团中的困难,他就一笔带过了。而且,他似乎完全忽视了暗物质理论对微波背景辐射角功率谱和大尺度结构功率谱的成功预测(这是MOND理论所没有预测的)。他津津乐道有了相对论模型RMOND,却闭口不谈此前的TeVeS模型直接被引力波观测所证伪。RMOND理论虽然可以给出满足宇宙微波背景辐射和引力透镜观测的结果,但毕竟是个“马后炮”,而暗物质理论则是早在观测之前就成功地给出了这些预测。
我个人的看法是,暗物质与MOND模型的竞争是良性的。如果公平全面的看待各方面的证据和说服力,目前暗物质模型大概还是略胜一筹,因此处在主流的地位上也并不奇怪。另一方面,MOND理论能够很好地解释星系尺度上的各种现象,也是非常有趣并值得玩味的理论。
参考文献
[1] , retrieved Sept. 11, 2021
[2] M. Milgrom, 1983, ApJ 270, 365; ibid. 371.
[3] M. Sanders & R. Verheijen, 1998, ApJ 503, 97
[4] J. D. Bekenstein, 2004, PRD 70, 3509
[5] C. Skordis, T. Zlosnik, 2021, PRL 127, 1302
[6] C. Skordis, T. Zlosnik, 2019, PRD 100, 4013
[7] D. Clowe, A. Gonzalez, M. Markevich, 2004, ApJ 604, 596
[8] B. Moore et al., 1998, ApJ 499, L5.
[9] J. F. Navarro, C. S. Frenk, S. D. M. White, 1996, ApJ 462, 563
[10] A. Drlica-Wagner et al., 2020, ApJ 893, 1
[11] A. R. Wetzel et al., 2016, ApJ 827, L23; T. Kelley et al., 2019, MNRAS 487, 4409
[12] P. Van Dokkum et al., 2018, Nature 555, 629
[13] B. Famaey, S. McGaugh, M.Milgrom, 2018, MNRAS 480, 473; Kroupa et al.,2019, arxiv:1903.11612
[14] Safarzadeh & Loeb, 2021, arxiv:2104.13961; J. Freundlich et al., arxiv:2109.04487
[15] David Merritt, 2020, A Philosophical Approach to MOND—Assessing the Milgromian Research Program in Cosmology, Cambridge University Press.
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 