世间万物的复杂性，很多就是从一些简单的规则开始，通过系统自发的相互作用产生，这就是神奇的自组织。自组织现在被发现出现在自然科学乃至社会科学的诸多领域，本文主要介绍数学上最早的概念模型：阿贝尔沙堆模型。

撰文 | Jordan Ellenberg（威斯康星大学麦迪逊分校数学教授）

编译 | 许钊箐

你听说过多米诺骨牌理论（Domino theory）吗？这是冷战时期美国为遏制共产主义提出的地缘政治理论，指社会主义国家会辐射影响周边国家进行社会主义变革。此理论极大地影响了美国二十世纪中期的外交政策，被用来为其霸权主义行为正名。但抛开政治理论，在自然界确实也有类似的多米诺骨牌行为，从物理学的角度上讲，它应该被称为 “沙堆理论（sandpile theory）”。

现实世界的政权转变往往不是有条不紊的发生，而是在突然间的协调配合下发生的，比如阿拉伯之春以及东欧剧变（最终苏联解体）。这些历史事件中，平静的时期里暗藏危机，然后在某一刻陡然倒塌。就像沙堆一样，假如你在一个沙堆上顶部再放一些沙砾，沙堆可能在短时间内没有明显变化。但是，顷刻间，类似于一场雪崩，顶部的沙砾会以不规则的方式突然冲下，并且在过程中很可能引发小的次级流沙。

这个比喻不一定会给我们带来什么。毕竟，真实的沙子很难去分析，就像现实世界的政治一样。但奇迹也在这里，物理学家巴克（Per Bak），汤超（Chao Tang）和维森菲尔德（Kurt Wiesenfeld）在1987年提出了一种由沙堆的抽象而来的 “阿贝尔沙堆模型（Abelian sandpile model）”。这种模型在保持足够简单以便于应用数学来研究的同时，似乎又可以刻画真实沙堆的一些有趣但无序的特点，并且适用于其他一些源自生物学、物理学以及社会科学的复杂系统[1]。

阿贝尓沙堆模型

它的过程是这样的：我们可以想象一个无穷网格，在每一个网格上都有一小堆沙子，并在每一个格子内用数字表示沙砾的数目。

但在垂直方向沙堆的高度是有一定限制的。所以这里假设每当网格中沙砾数目到达四，则四粒沙砾会向周边四个格子流散。所以如果初始是两个网格中有四粒沙砾：

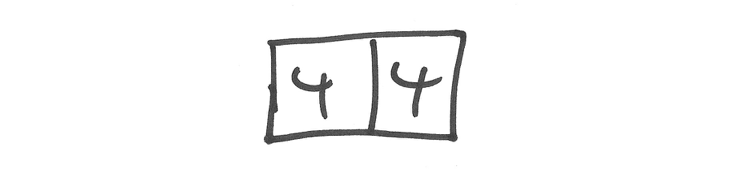
则沙堆流散之后左侧的网格变成了：

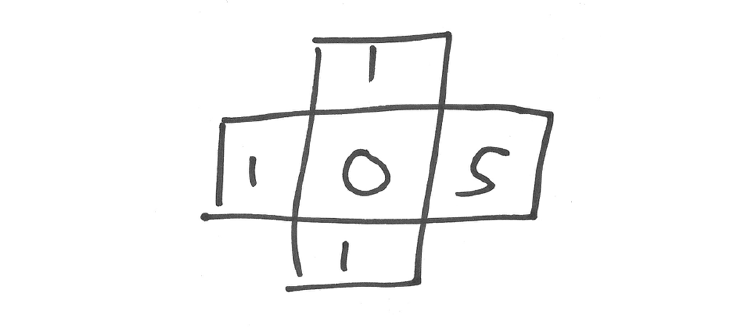
此时右侧网格已经超过四粒的沙堆，那么它会继续朝周边的四个网格各流散一粒沙砾：

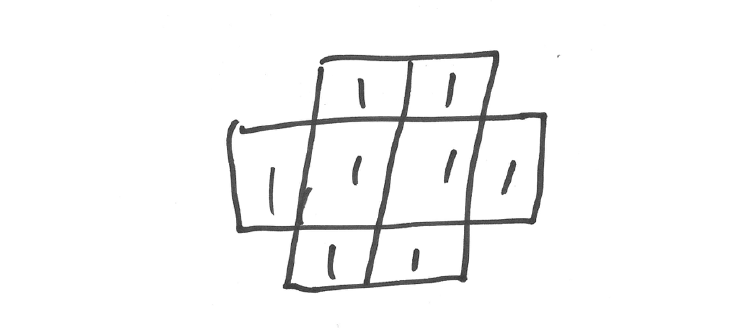
现在因为所有位置的沙砾数目都不超过四，每个网格点都处在稳定的状态，所以沙堆流散的过程就停止了。

以上的分析过程中，我们先进行的是原本两个网格中左侧的流散，其次是右侧的。我们如何知道哪个网格应该先向四周流散呢？好消息是，选择的顺序并不重要。因为我们可以由稳定状态网格的对称性得出，这种“阿贝尔沙堆”的最终状态并不取决于我们选择模拟流沙网格的顺序。这也是其取名为阿贝尔的原因，意味着我们选择的先后顺序不影响最后的结果。[译者注：数学命名中的阿贝尔通常是为了纪念挪威数学家尼尔斯·阿贝尔(Niels Henrik Abel，1802-1829)。他开启了许多领域的研究，并以证明五次方程的根式通解不存在以及椭圆函数的研究闻名。尽管他数学成就极高，但其生活遇到了很多困难，最后因肺结核不满27岁逝世。]

比如说，加法这种运算是阿贝尔的，我们指加法中元素是可以交换的：先加2再加3等价于先加3再加2。但是大多数的运算或操作都不是阿贝尔的。比如说先解锁汽车，再拉开车门，那么车门就打开了；但是先拉车门，再解锁汽车，得到结果完全不同——车门还是关闭的。所以沙堆的阿贝尔性质可以算是一个惊喜。

那么你可能会问，如果我们在一个网格上放很多很多沙砾，比如说一百万粒，会发生什么？当沙砾向四周不断流散，最后稳定下来时会是什么样子？你可能会想象最后会是一个巨大平整的沙堆，其中接近中心的一个很大的区域会有很多包含三个沙砾的网格。

但并不是这样。下面这幅图展现了最终稳定后的网格情况：

百万沙粒：中心点上堆积大约大量的沙砾 (准确地说是2的20次方)来模拟一个阿贝尔沙堆。(颜色表示堆高。蓝色表示没有沙子。紫色表示一粒，黄色表示两粒，褐红色表示三粒。)丨图片来源：Wes Pegden

好吧，会不会是一百万不足以使得沙堆数量是光滑变化的？如果我们用十亿粒沙砾呢，会得到一个平坦的大的沙堆吗？最终的图像是这样的：

十亿粒沙砾模拟图丨图片来源：Wes Pegden

我们期待的平坦情况没有出现。相反，那些奇异的分形图样持续存在。在接近中心的地方，复杂的图案就像是一个圆顶，其内部还镶嵌着很多格子，看起来是某种几何图案但又像是随机的；在沙堆的边界，则是众多一致的三角形，以规则的模式紧密连接。

这些图片是由卡内基梅隆大学的数学教授Wes Pegden及合作者康奈尔大学的Lionel Levine和Charlie Smart在沙堆的前沿研究中绘制的[2]。在Pegden教授的网站上，甚至可以看到十亿粒沙堆的交互式的图片，我们可以将其放大或者移动到任何位置再放大，比如直接观察沙堆的中心：

十亿粒沙堆的中心图像丨图片来源：Wes Pegden

或者看到外缘尖锐怪异的细节：

十亿粒沙堆的边缘图像丨图片来源：Wes Pegden

如果仔细观察，你还可以观察到更精细的局部结构。像很多数学文章一样，我们在这里给感兴趣的读者一个家庭作业：沙堆稳定之后，请说明两个邻近网格为什么不可能同时为空？（有答案！）事实上，一些实验表明，我们可能有更强的结论：空的网格不仅不会相邻，它们甚至倾向于不接近彼此，就像带相同电荷的粒子，它们会相互排斥。

(点击空白处查看参考解答)

▼

参考解答：假设现在有相邻的格子1和格子2。并且两个网格在沙堆的内部而不是边缘，所以我们不妨假设格子1是两个格子中在稳定之前最后向四周流散的那个。那么当格子1中的沙砾向相邻格子流散时，格子2就会包含一粒来自格子1的沙砾。但是因为格子1是最后流散的那个，格子2的沙砾并没有流失，因此两个格子不会同时为空。
 

复杂中所蕴含的简单规律

在你真的去拿显微镜观察沙堆之前，我不得不提醒你，真正的沙堆是不会产生这种自发性的结构的[3]。这里的阿贝尔沙堆模型甚至不具有模拟真实物理材料的性质。相反，我们看到的所有复杂性都来自于一个抽象、简单的确定性算法，甚至只用五行代码就可以写下。这不禁让人想到约翰·康威（John Conway）的《生命游戏》（Conway's Game of Life，https://playgameoflife.com/ ）。这个游戏也是从非常简单的规则中产生了丰富的复杂性。就像《生命游戏》一样，阿贝尔沙堆也是一个元胞自动机（cellular automaton）：它是一个微型的宇宙，其中的运行规律可以被计算机可接受的离散语言全然描述。在沙堆中，每个网格都具有从0到4中的一个数字，通过一个简单的规则决定相邻网格的值。而在《生命游戏》中，网格的状态更为简单，每个状态非生（值为1）即死（值为0）。

但是两者还是有区别的：《生命游戏》作为一种典型的元胞自动机，复杂的行为可以出现，但更倾向于简单的模式[4]；但是对于沙堆模型，我们似乎不需要特别设置初始条件，它就会自动趋向复杂的模式。

实际上，沙堆中复杂行为的出现取决于一个所谓的临界阈值，在这个值附近，往往会出现复杂的行为。我们对于自然界中的临界阈值这一概念是很熟悉的：水在较高温度下是一种无序的液体，但是当温度下降到达某个临界值，水就会发生巨大的转变——结晶成冰。而对于沙堆来说，它的密度就类似于水的温度。（这里的密度是指平均每个网格中有多少的沙砾。）如果有太多的沙砾，沙堆就会不稳定，“雪崩”随之发生；如果沙砾太少，沙堆则会很快稳定下来。那么多少算是我们说的太多呢？事实上，这个答案出乎意料的简单。巨大变化和微小变化的分界线是：平均每个网格里2.125粒沙砾。

值得注意的是，在网格有限，并假设当沙砾到达边缘格子时再流散就会消失的情况下，平均每个网格的沙砾数会是2.125。在一开始，所有的网格都是空的，我们一粒一粒地将沙砾放至中心的那个网格。一段时间后，沙堆开始向四周流散，会慢慢形成类似于我们之前展示过的Pegden教授生成的图像（这个图像是假设网格在所有方向都有无限多个。）我们扔下一粒沙，待沙堆稳定后，就再扔下一粒，这样沙砾会越来越多。但如果沙砾到达边缘，流散出去的沙砾就消失了。此后沙堆会接近一个平衡：沙砾在边界掉落的速率等于我们增加沙砾的速率，密度会在某个临界值稳定下来。当然，系统会有局部波动，随着时间推移，密度低的地方和密度高的地方会有一定的交替变化，但对于整体，平均每个网格沙砾数会在2.125粒左右。

如果一开始我们尽可能地将每个网格布满沙砾，即每个网格放置3粒，那会发生什么呢？这种初始布局是稳定的，但它是很脆弱的稳定。我们在任意一个网格放置一粒沙砾，之后一场巨大的“雪崩”就开始了，直到密度下降到2.125它才会停止。

那么，当沙砾密度到达临界值时会发生什么？这时的沙堆会处在最有趣的状态。向四周流散的过程一直在发生，但却不是持续的大范围混乱状态；相反，流散会出现类似于海浪一波接一波，不时也会发生罕见的横跨所有网格的雪崩灾难。而流散活动在阈值密度下的分布似乎遵从幂律，流散活动的频率和它的规模成反比。其中也有持续的流散活动，但它们是有某种结构和规律的。不仅如此，为了展示其复杂的行为，沙堆不需要做精细的调整，它自己具备调整的能力。不论系统从哪里开始，只要新的沙砾以常数速率增加，系统都会通向临界阈值状态。

眼见为实。美国国家标准技术研究所（NIST）的R.M. Dimeo就制作了一个系列沙堆处于临界状态的无聊电影。

沙堆中加入一粒沙子后的变化，颜色代表该处流散的次数，每次流散都会“更热”。视频来源：R. M. Dimeo

对我来说，这个过程看起来就像是有生命力的，而不是一个巧合。思考丰富的生命结构是如何从简单系统中涌现出来的，它们会自动寻找临界阈值，使用自组织临界性的概念是一种流行的方式。一些生物学家认为自组织临界性是复杂生物行为的潜在统一理论。这一理论支配着一群鸟儿同步飞行的模式，就像遗传信息支配鸟儿个体的发展一样[5]。理论生物学家斯图亚特·考夫曼（Stuart Kauffman）写道，“生命系统存在于临近混乱边缘的一个稳固的状态，是自然选择实现并维持了这种平衡状态。” 就像是我们讨论的沙堆。它当然不是一个生命，但它却生机勃勃，不是吗？

沙堆是第一个，也是被研究的最多的自组织临界性的例子。此外还有很多其他的例子。（在Pegden教授的网站上还有一些。） 但是，我们并不知道沙堆的散落规则到底是什么，为什么它使得系统不可避免地朝着复杂的临界状态发展；也不清楚哪些元胞自动机可能表现出这种自组织临界性。

一些深刻的理解可能会从沙堆理论和其他数学理论的惊人联系中产生。对于我这样的几何学家来说，沙堆理论与最近新兴的热带几何学理论（tropical geometry）有关，该领域的目标是用类似的离散几何现象来模拟连续的几何现象。[译者注：热带几何学理论是首先由巴西数学家及计算机科学家伊姆雷·西蒙（Imre Simon）于1980年代发展，“热带”一词源于部分法国数学家对于巴西的刻板印象。热带几何可以看成是分片线性化的代数几何，在计数代数几何中有重要的应用。]

对于概率学家来说，沙堆与所谓的生成树密切相关。生成树（在方形网格上）是一个分支路径，它接触网格上的每个点，但不会形成闭合的回路。无论这些理解是来自于哪里，沙堆理论提醒我们，数学中非常有趣的现象，就像物理学很多有趣的现象，经常出现在相变之中。就是在这里，我们处于两个不同的数学理论之间，既拥有它们的特征，又可以跨越边界传递信息和问题。当然通常来说，问题总是比答案多。

参考资料

[1] Bak, P., Tang, C., & Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Physical Review Letters 59, 381-384 (1987).

[2] Levine, L., Pegden, W., & Smart, C.K. Apollonian structure in the Abelian sandpile. preprint arXiv.:1208.4839 (2014).

[3] Mehta, A. & Barker, G.C. Disorder, memory and avalanches in sandpiles. Europhysics Letters 27, 501-506 (1994).

[4] Aron, J. First replicating creature spawned in life simulator. New Scientist 2765, 6-7 (2010).

[5] Mora, T. & Bialek, W. Are biological systems at criticality? Journal of Statistical Physics 144, 268-302 (2011).

本文译自Nautilus “Dominoes” 2015年4月刊

https://nautil.us/issue/107/the-edge/the-math-of-the-amazing-sandpile