在数学教程中如何给出定义，经常是值得研究的。好的定义应当揭示概念的本质，是“what”层面的，而不是“how”层面的。

撰文 | 姜树生

本文所讨论的数学问题，主要与数学教育有关。

对于一个数学概念的理解，直观、定义与表达这三个方面都是需要的，但有各不相同的作用。

在小学数学的初级教程（具体说就是自然数的认识）中，这三个方面是混合在一起的，既要有直观（从扳着手指头数数开始，实际上要做很多实验），又要学记数法（进而就可以计算），最终要形成自然数的概念。在这个过程中，难免有不适当的做法，甚至走弯路、犯错误，但如果最终形成了自然数的概念，在学习过程中有些缺点出些错误都无可非议。就如孩子学走路，难免跌跌爬爬，磕磕碰碰，甚至受点伤，但只要最终学会走路就行。

然而近年来，有些自以为高明的教学法，从很小就教孩子学习记数和计算，不重视甚至忽略直观。其结果可能使得孩子在速算比赛中获奖，但却不能自觉地应用数学解决生活中的问题，更没有培养创新能力。其实只是一种虚荣而已。

到了中学数学教程中，上述三个方面逐渐分开，教学法与小学有显著的不同。

首先来看无理数的概念。在早年的大多数教科书以及当今的一些教科书中基本上是这样讲的: 首先以例子说明无理数存在，具体说就是有的“数”不等于两个整数的比，最常见的是边长为 1 的正方形的对角线的长度（有的教科书中给出其无理性的证明）。认识到无理数的存在，就可以进一步形成实数的概念，即有理数与无理数的全体。至于无理数表达为无限不循环小数，很多教科书是不讲的，或者仅举具体的例子让学生体会。这样的讲法尽管没有给出实数的定义，却是适合大多数学生。实际上大多数人一辈子也没见过实数的定义，但这并不妨碍他们在工作中使用实数，因为数学的严谨性是由数学家保证的，一般人尽可以放心大胆地使用。

但是，如果有学生问“什么是无理数”，准确地说就是不满足于直观，希望从根本上搞清楚实数的概念，教师应该怎样回答呢？这样的学生是千里挑一，而能回答这样问题的中学教师也是千里挑一。问题仅在于千里挑一的学生能否遇到千里挑一的老师。

有的老师会回答说：“无理数就是无限不循环小数”，在有些教科书或课外书中也看到这样的“定义”。然而，“无限不循环小数”只是无理数的一种表达方式，而不能作为定义。从哲学上说，任何一个定义必须是针对一个客观存在的对象,否则就可能落入逻辑陷阱。（一个典型的例子就是“所有集合的集合”，若引入这个“定义”，整个数学体系就崩溃了。）首先需要明白实数是一种客观存在，然后才能谈它的表达。

有效的实数定义至少有两个，一是用戴德金分割，一是用基本叙列。两个定义是相互等价的，但风格迥异，前者几何味较浓，后者代数味较浓。（从数论的眼光看，实数是整数在“阿基米德位”的局部化。）要想理解实数的实质，最好两个定义都读懂（若能从数论的角度理解当然更好）。但这两个定义都颇不简单，而且定义后还要建立各种运算、大小关系、极限等。对于一般的中学生甚至大学生，难度都是相当高的。因此，在中学数学教程和大学高等数学教程中不引入实数的定义，是明智的。

但若在中学或大学数学教程中以“无限不循环小数”作为无理数的定义，则是非常不明智的，非但不能使学生明白，反而会使很多学生误以为懂了。如 [4] 中所说:

“不怕不懂，就怕不懂还自以为懂。”

再来看平面几何。在几何教科书中有很多定义，但这些定义都不是“原始”的，原始的概念如点、直线、平面等都是只有直观没有定义的，但它们由公理体系界定。用现代的语言，几何对象可以定义为满足一些条件 (公理) 的若干集合所组成的体系。硬要定义直线、平面等是不会有好结果的，所幸还没听说有这样的教科书。

不过在现行中学数学统编教科书中，很多几何概念的定义有严重缺陷，例如把直观当作定义，或语义含混 (详见 [2])。

回过头来再看实数的概念。非常值得一提的是数轴的直观。将实数理解为数轴上的点，对于大多数学生是理解实数（包括无理数）的一个有效途径。有了无理数的例子，再有数轴的直观，对于普通学生就可以有效地讲授实数概念。换言之，几何直观是理解实数的一个有效途径，对于中学生是不可或缺的。

对于多数学生有较高难度的定义还有一些，如概率。对于这类概念，只讲直观而不讲定义，常常是明智的。但常常还需要给出表达方式，并进一步给出“操作”（如计算）方法。这样学生就能够运用这些概念，做出有创新性的工作，尽管可能最终也没有完全搞懂某个概念。此外，通过应用也有可能提升对于概念的理解。

简言之，如果学生能理解，直接讲定义对于建立数学概念最有效；而若大多数学生不能理解，最起码也不应该讲假的定义，或者忽悠学生。

在大学数学教程中也有定义方面的问题。

先来看微积分教程。随便找一本微积分（或数学分析）教科书，就会看到其中积分（黎曼积分）的定义颇不简单。在数学分析教程中，一元函数的积分定义为一个颇不平凡的极限，判别其存在性还要用到达布和等，相当复杂而费解。在非数学专业的微积分教程中，这部分内容只是简化了些（实际上是偷工减料），复杂度基本未变，所以未必比数学分析教科书容易懂；但另一方面，对这些内容都不会布置作业，更不会考试（包括研究生入学考试），徒然浪费时间且让学生头疼。

顺便指出，各版本中学教科书中的积分概念也是这样写的，对于中学生当然就更头疼了，甚至很多中学教师也看不懂。

学过实变函数论就知道，一元函数黎曼可积等价于几乎处处连续，直观地说，其实离连续函数没多远。在黎曼积分的应用中实际上主要是针对连续函数，至多是分段连续函数。对于一般的学生，由黎曼积分其实只是学到面积的一个定义，何况这还不是一般的定义，例如一条一般的约当单闭曲线所围成的区域的面积，就不能用黎曼积分来定义（在康妥的时代就知道，曲线可能有非零的面积）。所以，花了那么多的时间那么大的功夫学黎曼积分，只是学到一个特殊情形的面积定义而已。然而，一般人都有面积的直观，并不需要面积的定义。（如果关心面积的定义，可以看勒贝格积分或更一般的定义，如动力系统中对于维数和测度的定义。）因此，为了理解积分的概念，至少对大多数学生，不如局限于连续函数的积分。

如果将连续函数的积分定义为“有向面积”，就很容易理解且不需要花多少功夫。具体说，对于闭区间 [a, b] 上的连续函数 f(x)，由直线 x=a，x=b，y=0 和曲线  y=f(x) 围成的图形具有面积，将直线 y=0 上方的面积看作正的，下方的面积看作负的，这样得到的总面积称为有向面积。将 f(x) 在 [a, b] 上给出的有向面积称为它的积分，记为
 

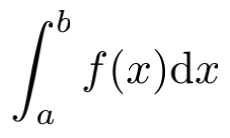
由此定义不难证明牛顿-莱布尼兹公式
 

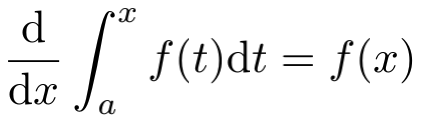
而积分的一些其他基本性质如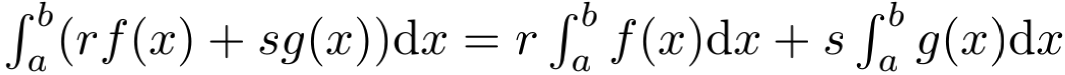  (r, s为实数)，分部积分法、换元法以及一些初等函数的积分等，利用牛顿-莱布尼兹公式都很容易证明 (有些甚至可以作为习题)。利用张景中先生制作的辅助软件，一堂课就足以讲清楚积分的基本概念和牛顿-莱布尼兹公式，这已经超过中学课程标准的要求了。至于黎曼积分的原始思想——分割成竖条作面积和再取极限，可以直观地讲一下，不讲也可以，不需要花费很多课时，其实只有少数学生会关注。

再来看线性代数教程。“向量”是最重要的基本概念之一。在目前所见到的很多教科书 (其中有些是早年的) 中，向量定义为有序数组。这样的定义不仅费解 (与解析几何中的定义相距甚远)，而且向量的运算还要另外定义。一般说来，要直到学了很多内容后才明白向量是什么。

这样的定义有明显的缺陷，没有揭露向量的本质。详言之，有序数组是向量在取定的坐标系下的表达，是“how”层面的，而好的定义应该是“what”层面的。

从“what”层面看，向量就是向量空间的元素，脱离向量空间来讨论向量是没有意义的。向量的运算，都涉及多个向量以及它们之间的关系。所以，要明白什么是向量，归根结底要明白向量空间。

然而，很多线性代数教科书中根本就没有向量空间。即使有，很多教师也不讲。常见的理由是，向量空间太“抽象”，学生难以理解。那么，基于向量空间的很多概念和定理，当然就更不能讲了。

其实向量空间的概念并不算很“抽象”，国外一些大学本科代数教科书是先讲群论后讲线性代数，显然比我国的线性代数或高等代数教科书更“抽象”。另一方面，我国现在的中学生都要花很多工夫学集合，但从教科书上看不到有什么用（除了刷题）。若是对于向量空间概念的高明之处有所领悟，至少会觉得集合是有用的。所以，至少有一部分学生理解向量空间并无困难。而对于有困难的学生，需要教育者的耐心，例如可以采取如下的途径讲授。

注意学生在解析几何中学过平面向量和空间向量，而且知道一些物理应用。在初等的数学和物理教科书中一般会讲向量的直观，即“既有大小又有方向的量”，而且较好的教科书中还会指出，这只是一种直观，并非既有大小又有方向就是向量 (例如电流)。学生通过物理意义可以对向量有正确的理解，尽管还没有向量空间的概念。那么，从向量的这些直观概念推进到一般的向量空间，本质上只是维数可以不受限制。因此，可以先复习解析几何中的平面向量和空间向量，包括它们的直观意义和物理应用，然后系统地复习和整理向量的运算，再复习和整理向量在直角坐标系下的表达。然后举例说明高维的向量也是有数学和物理意义的。由此引导到一般的向量空间，就不很“抽象”和难于理解了。当然这需要多花费一些时间，但对于后面的学习是有利的。

也许您会反驳说：“把向量定义为有序数组，我没觉得费解呀，而且很容易很方便。”好的，那我们接着往下看。您总不至于停留在向量水平吧，那么下面要理解张量。按照“有序数组”这个路子，很多教科书是这样定义张量的: 一个n维r阶张量由一组数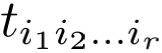组成，其中每个脚标取1至n的整数，所以共有nr个数；如果用一个n×n-矩阵 (aij) 改变坐标系，则各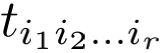需要做一个以aij的函数为系数的坐标变换 (具体的变换公式甚为复杂且与张量的共、反变性有关，此处从略)。您还觉得这样的定义不难理解且方便吗？

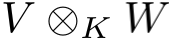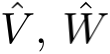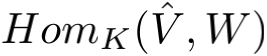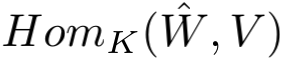如果理解了向量空间，那么要理解张量只需要再往前走一步，例如将域K上的两个向量空间V, W的张量积 定义为它们的对偶空间 上的所有 K-双线性函数组成的空间，它同构于 ，也同构于。有了张量积就很容易定义张量了 (参看 [3])。这样直接从“what”层面理解，显然容易得多也简单得多。

还值得指出，一般不能说定义的对错（Yuri Zarhin 曾无奈地说: “Well，every definition is correct”），只能说定义的优劣。一个好的定义能够揭示客观存在或自然规律，启迪思维，引导有意义的研究方向。在极端的情形，甚至一个好的定义就解决了问题。遗憾的是很多定义有缺陷。有的教科书将直观当作定义，毫无科学严谨性可言，有些还颇为费解，或语义含混，或几乎是同义反复（参看 [2]），这些都是误人子弟。有些定义虽然严谨，但没有背景，不自然（有人为设置的条件），在极端的情形甚至所定义的东西根本不存在。尽管由这样的定义可以推导出一些定理，可以写论文发表，但对科学并无贡献，也不会有应用，只是逻辑游戏而已。还有一类情形，虽然所定义的对象是客观存在且值得研究的，但定义的条件复杂或费解（如上面所说的将表达作为定义），尤其不利于初学者。其中有些还可能导致偏见或心理障碍。

由上所述可见，在数学教程中如何给出定义，经常是值得研究的。这是张景中先生所说的“教育数学” (参看 [6]) 的一个课题。

参考文献

[1] 姜树生: 谈数学教育的特殊性——兼谈如何处理数学与教育学的关系. 数学通报 2008 年第 4 期

[2] 姜树生: 现行统编中学数学教科书有多烂 (2016)

[3] 李克正: 《抽象代数基础》，研究生数学丛书 6. 清华/Springer 出版社 (2007)

[4] 李克正: 现代社会对于劳动者的数学素质的需求 (2019)

[5] 其故: 得数学者得天下. 返朴网 (2019)

[6] 张景中: 谈谈教育数学 (2021)