在欧几里得的《几何原本》中，有一条明显与众不同的公理，即第五公设，现代称为平行公设：如果一条线段与两条直线相交，在某一侧的内角和小于两直角和，那么这两条直线在不断延伸后，会在内角和小于两直角和的一侧相交。要“证明”它，人们发现连直线本身的定义就有瑕疵，在耗费了数学家近两千年的时间后，关于直线、空间等基础的概念彻底发生了变化，我们彻底打开了一个新世界——非欧几何，这正是这条复杂公理里蕴藏的智慧。这篇文章将介绍一些关于探索第五公设的早期历史，我们可以看到几何学的深刻从此展露出来。

本文经授权节选自《尖叫的数学：令人惊叹的数学之美》（湖南科学技术出版社）第六章《非欧几何的世界》。本文标题和小标为编者所加。点击文末“阅读原文”可购买此书。点击“在看”并发表您的感想至留言区，截至2022年1月2日中午12点，我们会选2条留言，各赠书1本。

撰文丨翁贝托·博塔兹尼（Umberto Bottazini）

翻译丨余婷婷

1919年11月7日，伦敦《泰晤士报》中有一篇报道，其标题为“科学的革命，宇宙新理论，牛顿的思想被彻底推翻”。到底发生了什么具有重大变革性的事？同年5月，天文学家亚瑟·爱丁顿（Sir Arthur Stanley Eddington，1882-1944）和弗兰克·戴森（Frank Watson Dyson，1868—1938，他为证明爱因斯坦的广义相对论起了重要的作用）分别前往几内亚的一个海岛和巴西，观测了日全食现象，11月6日，在一场注定会被历史铭记的皇家学会会议上，他们交流了观测结果，而观测结果证实了广义相对论的预言：太阳的质量使光线在空中发生了偏折。全世界的新闻媒体接二连三地转发这则新闻，爱因斯坦一夜成名。“世界历史上的一个新伟人！”某个柏林报刊在爱因斯坦的照片下配上了这样的文字。《泰晤士报》援引皇家学会主席的话，写道：1846年海王星的发现强有力地证实了牛顿定律和欧氏几何的正确性，而广义相对论是继发现海王星之后最重大的事件。

如今，“关于宇宙这个大工厂的科学观点应该做出改变了”，以和“人类思想最重要的表述，或者说最重要的表述之一”——相对论达成一致。爱丁顿认为相对论是“展现数学推理力量最好的例证之一”。一个天才数学家在19世纪中期的一个宿命时刻预测的空间观，引发了一场激动人心的变革的高潮，在两千年后，先于牛顿推翻了唯一的欧氏几何理论，解放了几何学家，打开了他们创造性的想象。

什么是直线？

这个“宇宙工厂”不再遵循欧氏几何理论了？空间几何也不再是欧几里得给我们解释的那个空间几何吗？光线的轨迹也不是直线的？怎么可能呢？如果你们感到难以置信，这是很正常的，因为你们的生活经验告诉你们的恰恰是空间遵循欧几里得定理、光线沿着直线传播。但什么是空间呢？等会儿我们听听康德是如何定义它的。在尝试定义空间之前，你们要知道，连欧几里得都没有做过这件事。欧几里得在《几何原本》中研究了立体的特性，但是并没有给出空间的定义。他只是说立体是“一个有宽度、长度和深度的东西”，也就是说它有三个维度。最初几条定理讲的是相交于一条直线的几个平面，或者平面上的一条垂线，等等，从这些定理中，我们可以凭直觉领悟出空间指的是什么。那什么是直线呢？这提的什么问题呀！直线是什么，我们所有人都以为自己在学校里已经学过了。这没错。

那你们自己试着去定义它吧。某个直的（或者说，不是弯的）东西，如果你们给出的定义跟这个差不多，那就不必说了。你们也许会为自己辩解，说自己不是数学家。那你们能够聊以自慰的就是，这个难题也同样困扰了数学家们几百年。数学中经常出现的一种情况就是，那些看似最明显和熟悉的概念，反而最难给出严谨的定义。杰出的百科全书式学者和数学家达朗贝尔写了一句很有名的话。他在1795年写道：“直线的定义和特性，如同平行线的定义和特性，这么说吧，是几何原理中的障碍和家丑。”至于吗！当然了，因为整个欧氏几何都建立在这些定义和特性上。难怪在达朗贝尔眼里，给直线和平行线下定义的事成了一件丑闻。

达朗贝尔补充说，直线的普通定义就是两点之间最短的线。如果你们想一想，或许会赞同他给出的定义。这位法国学者接着说，可这个定义看起来更像是直线的特性而不是原始概念。你怎么知道它是最短的那条呢？谁说从一点到另一点只有一条最短的路径呢？我们之所以赞同这个直线的概念，只是因为它隐含了这个事实。如果我们无法对直线下一个令人满意的定义，那我们也不可能给出平行线的定义。达朗贝尔的提示似乎为我们指明了道路，他说：一条直线的平行线是位于直线同一侧且距离直线相等的两个点所连成的线，与该直线位于同一平面。未经论证而设定它是真的，就是设定某样定义之外的东西。又回到了原点，我们仍在讨论距离的概念。达朗贝尔总结说，总之，“平行线理论是几何原理中最不易跨越的难点之一”。

麻烦的“第五公设”

从大约公元前300年起，无数几何学家呕心沥血，尝试解决这个难题。欧几里得在《几何原本》中确立了几何准则。在他给出的定义中，“直线是与其重合的每一个点所连成的线”。你们也许会觉得这个定义不是很清晰。他不该遗漏直线是两点间距离最短的线，但只有阿基米德明确设定了这一点。至于平行线，欧几里得认为，它们是位于同一平面，两端无限延长却永不相交的直线。

《几何原本》中的前三条公设（在任意相异两点之间能作且只能作一直线；直线两端可任意延长；给定任意圆心和半径可以作圆）确保了构造基础几何图形的可能性。第四公设为所有直角都彼此相等。而第五公设，即所谓的平行公设，第一眼看上去很是与众不同：同一平面内的两条直线与第三条直线相交，若其中一侧的两个内角之和小于两直角和，则该两直线无限延长后必在这一侧相交。你们在纸上作个图，就会一目了然了。然而，你们可能会认为这条公设根本不是那么显而易见，在概念上比起前四条，无论如何都要复杂得多。达朗贝尔口中“几何的障碍和家丑”，说的就是这条公设。可它至关重要，因为正方形的构建、毕达哥拉斯定理的证明以及由它推演出的其他所有定理，都以这条公设为基础。

公元5世纪，普罗克洛在为《几何原本》撰写的《评注》中说，很早之前就有学者认为，通过其他四条公设，可能再加上一条比欧几里得公设更简单易懂的新假设，就能证明第五公设。接下来的数个世纪，众多数学家都向欧几里得公设发起了挑战，可他们绞尽脑汁也无法给出证明。

在他们之中，有人认为平行线的概念直观易懂，有人认为要运用图形的相似性，还有人想用普罗克洛提出的新公理代替第五公设，即“过直线外一点无法作出两条与已知直线平行且不重合的直线”。你们或许在课本里学到了它的等价公理：“在平面上，过直线外一点只能作一条直线与已知直线平行”。可你们如果仔细想想，就会发现普莱费尔（John Playfair，1748-1819），在18世纪末提出的这条公设比欧几里得的平行公设还要复杂。它们俩是对等的，意思就是说从第五公设可以推导出普莱费尔的公设，反之亦然。从波斯数学家欧玛尔·海亚姆（Omar Khayyam，1048-1122）和纳西尔丁·图西（Nasir al-Din al-Tusi，1201-1274），到17世纪末的约翰·沃利斯（John Wallis，1616-1703），再到18世纪末的阿德里安-马里·勒让德（Adrien-Marie Legendre，1752-1833），许多欧氏几何的“改良者”所提出的公理假设都存在这个问题。

还有学者试图使用反证法证明第五公设，比如耶稣会士吉罗拉莫·萨凯里（Girolamo Saccheri，1667-1733）。反证法是一种论证方式，如果从论题A的反论题可以推演出A，那么论题A为真。萨凯里说：“这似乎是所有真理的首要特点，从假设真理的反面为真，通过令人惊叹的反驳和推论，最终又回到了真理本身。”萨凯里在《免除所有污点的欧几里得几何》（1733年）一书中研究了一个带有双直角的等腰四边形，即∠A和∠B为直角，AD=BC。

那∠C和∠D怎么样呢？首先一目了然的是它们的大小相等。此时，你们或许会想到三种可能性：∠C和∠D都是直角，或者都是钝角，又或者都是锐角。其中的每一种可能（萨凯里把它们叫作假设），都具有普适性，就是说如果它适用于某一个双直角的等腰四边形，那么它对其他所有双直角的等腰四边形都成立。

关于直角的假设就是欧几里得所说的公设，ABCD是一个长方形，自然满足第五公设。运用反证法，萨凯里证明了“钝角的假设是错误的，因为它会破坏图形本身”。还剩下锐角这个“敌对假设”，只有它还违背欧几里得的公设。为了打败它，萨凯里投入了一场“长久的战役”，写满了一页又一页晦涩难懂的推论，最终得出了结论——那个假设“是完全错误的，因为它与直线性质相矛盾”。你们看见了吗？我们回到了起点：又一次涉及直线的“性质”。这个“性质”是什么呢？那个假设所导出的结论，与人们看到直线时的最初感受相矛盾，萨凯里难道不是在避免承认这点吗？

在这场“战役”中，萨凯里阐明和论证了一堆令人意想不到的新定理，因此有后人称他为非欧几何的“先驱者”。但萨凯里并不是另一个哥伦布。哥伦布本要寻找去往印度的新航线，却发现了新大陆，而萨凯里却坚信自己成功制服了锐角这个“敌对假设”，肯定自己抵达的地方就是“印度”。因此，保尔·瓦雷里（Paul Valéry，1871-1945，法国作家、诗人）对“这个萨凯里”所表现的带有讽刺意味的惊讶就显得不太恰当了：“萨凯里为未来一种大胆创新的几何学稍稍推开了大门，却不承认”，因为事实上“他就是一个完全的耶稣会士”。可萨凯里在命题上并不是“耶稣会式”的，反而对欧氏几何有一种“托勒密式”的信仰。无论如何，尽管萨凯里十分确信自己的论证，可他并没有为欧氏几何去除任何污点。如果说第五公设是欧几里得空间科学这件衣服上的污渍，那么这块污渍依然存在。然而，用伊姆雷·托特 的一个恰当说法来说，应该是这位耶稣会士的努力使“几何学变得不再单纯”。令人反感的使几何变得不再单纯的第五公设被公开阐明并得到全世界的认知，还要等待一个多世纪。

不止三维

身在哥廷根的克吕格尔（Georg Simon Klügel，1739-1812）认真研读了萨凯里的研究成果。1763年，他还在论文中讨论了萨凯里的研究。那他得出的结论是什么呢？“就目前而言”，面对他这样的“纯粹真理的捍卫者”，我们至少可以说“没有哪个头脑健康的人会否定欧几里得公设”。没错，就目前而言。受克吕格尔的论文启发，朗伯沿着萨凯里的足迹出版了《论平行》（1776年）。这个朗伯就是那个证明了π是无理数的朗伯。数学家用弧度表示角的大小，而数字π还表示平角的度数，即180°。和萨凯里一样，朗伯也试图证明锐角的假设不成立却终告失败，这次他构想了一个有三个直角的四边形，论证的是第四个角。

在讨论钝角的情况时，朗伯从球面三角学中得到启发，猜测长度的绝对度量的所有可能性。球面上，由三条大圆的弧所包围的区域称为球面三角形。球面三角形不存在相似性，也就是说相似的球面三角形彼此完全相同。球面三角形的三个内角α、β、γ的和大于180°，即大于π；三角形的面积由公式R2(α+β+γ-π)可得，R为球的半径。长久以来，这两点众所周知。那锐角假设的情况如何呢？这次内角和不再“过量”，反而“不足”，小于π，面积公式为r2[π-(α+β+γ)]，r为常数。“由此，我几乎可以得出结论：这个假设存在于某个虚半径球体上。”朗伯带着些许犹豫，终于大胆地说出了自己的想法。的确，如果R=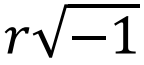，球面三角形面积公式R2(α+β+γ-π)就会变成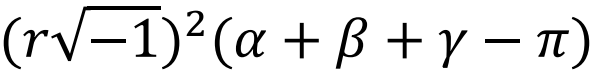=r2[π-(α+β+γ)]。

无论如何，谨慎的朗伯决定不出版他的这本著作，直到他逝世以后的1786年，这本书才问世。和萨凯里的结论一样，朗伯的结论也和普通的空间概念相矛盾。朗伯与康德保持着密切的书信交流，我们可以在康德那里找到关于空间的表述。这位来自柯尼斯堡的哲学家在《纯粹理性批判》（1781年）一书中判定：“空间并不是从外部经验之中抽引出来的经验性概念。”“它作为一切外部直观的基础，是一种必然的先天表象。”“所有几何原理的无可置疑的确定性”就建立在这种先天必然性上。不必多想，康德口中的这个几何，自然是欧氏几何。

一百年后，关于空间的概念依旧没有改变。陀思妥耶夫斯基笔下，伊万·卡拉马佐夫在与弟弟阿辽沙的一段漫长交谈中说：“假如上帝存在，而且的确是他创造了世界，那么正如我们所知，上帝是按照欧氏几何创造的世界，还创造了只有三维空间概念的人类头脑。”可从古时起，人们就知道球面几何并没有违背欧氏几何的公理，朗伯的阐释也说明了这一点。当时，非欧几何的消息应该也传到了圣彼得堡，因为伊万接着说：“但是以前有过，甚至现在还有一些几何学家和哲学家，其中不乏最出色的学者，他们怀疑整个世界，或者说得更大一些，整个宇宙是否真的只是依照欧氏几何创造的。他们甚至还质疑平行公设，大胆猜想：欧几里得认为永不相交的两条平行线，它们事实上可以在无限延长之后，相交于某点。”伊万陷入了困惑。最后这种定义平行线的方式，司汤达笔下的亨利·勃吕拉曾在一本“陈旧的教理问答手册”中学过，但与处于争议之中的著名的第五公设毫无关系。