情愿不自由，便是自由了。

（本文七千多字，三张图、两个公式，可以在20分钟内轻松读完）

撰文 | 孟子杨

一胡博士

时令不停流转，经过残酷阴沉荒原般的四月，到了五月，人们总会回过神来想起青年。想起身处初夏阳光中的感觉，看着满山茂盛的树木在微风中摇曳，看着蔚蓝的大海和视线尽头那一片氤氲中满是希望和新鲜的世界，多好，一切都是绿的、蓝的、清澈的、新鲜的、天真的、诚实的和健康的。

就是在这样的五月里，说来有趣，我总是想起一个人——胡适。倒不是因为胡博士是五四的健儿、民国的“大师”；也不是因为他有多大的学问，他的三部主要著作《中国哲学史大纲》、《白话文学史》、《四十自述》都是只有上卷没有下卷的半成品，从杜威（John Dewey）那里学来的实用主义哲学，基本上就是今天大学本科的水平；更不是因为他做出过多大的事业，当过驻美大使却经历国民政府对他的信任危机，当过北大校长却在翻天覆地的时刻仓皇逃离，最后中研院的院长，还没有展开手脚就因为心脏病发死在任上，其实一生都在动荡中度过，没时间和条件静下心来认真地完成事业。想起他，主要是因为他的天真、单纯，一生都是像个五月般的青年，说着些大家都知道是正确，却因为年岁的增长，因为在社会中摸爬滚打而变得世故，渐渐忘记的大白话、大实话。这些话和青年般的态度也许反而是他被人记住的地方，比如：

“大胆的假设，小心的求证。”

“多研究些问题，少谈些主义。”

“有几分证据，说几分话。”

再比如他写的那些白话诗，从文学的角度，确实不能和鲁迅、徐志摩、冯至以及后来的许多现代作者们相比，但是也十分清楚地体现着他一以贯之的青年之气，比如：

岂不爱自由？

此意无人晓：

情愿不自由，

便是自由了。

这是他决定接受包办婚姻，决定与从订婚到结婚的15年里从未见过面的旧式新娘江冬秀结婚前写的。对于彼时身在美国，正因为推动白话文革命而名满天下的新派人物“我的朋友胡适之”来说，我们很难想象为了接受这样的婚姻他的心里经过了怎样的波澜，但是一旦想通了，就接受命运坦然以对，在不自由的生活中不断寻找自由的寄托，努力创造新的生活和事业，这是青年人才有的乐观态度。再比如，

偶有几茎白发，

心情微近中年；

做了过河卒子，

只能拼命向前。

这是他在驻美大使任上，十分不情愿地以书生身份接受行政任务，而且还受着中美双方的猜忌，却又忍受着压力寻求各方支持中国抗战时写的。彼时他已经年近半百，心里整日想着完成几件能够传世的学术工作，但现实所迫不得不放下个人的兴趣，忍受着行政工作中的种种不快，以过河卒子般的决绝，任劳任怨地为了更大的目的服务，一如年轻时接受包办婚姻一样。当时美国还没有对日本宣战，胡适到处演说争取国际支持，以至于过度劳顿心脏病发险丧生命。这样拼命的精神，是“微近中年”的青年人才有的心态，全无今日诸多学者型官僚和官僚型学者的鸡贼和油腻。

二受限量子多体系统

如胡适这样的，在不自由中寻找自由的青年气魄，在量子多体物理学研究中也是十分需要的。量子多体系统中往往出现由于相互作用、晶格结构、 材料的物理与化学性质和实验探测手段等等限制所造成的约束问题，这类问题可以称笼统地称为受限量子多体系统，虽然是受限的，但其中却往往涌现出新的物理现象和行为。对于这些问题的求解，就是用青年的气魄，在限制中找到新天地的好例子。最近，笔者与合作者们就有幸参与了如此的一项研究工作[1]。从受限量子多体问题的计算和理论分析中，明白了一个基本模型的相图，解释了之前10多年中许多研究工作中的互相矛盾的结果，发现了一个人们之前没有意识到的新的量子物相，并且将量子多体算法、共形场论 bootstrap 研究的最新结果，还有拓扑序相变等等看似没有直接关系的领域联系起来，十分有趣。几个月来仍时时受到鼓舞，兴之所至，拿出来与读者诸君分享。

受限量子多体系统有很多具体的实现，比如阻挫磁体中由于几何的反铁磁相互作用而产生的基态自旋构型简并，或者最近比较火热的理德堡原子光晶格实验中，通过封锁（blockade）效应调控形成量子 Ising 相变[2]和 Z2 量子自旋液体纠缠态[3]等等。但是真正体现着受限量子多体问题的风神的，还要数量子二聚模型 (quantum dimer model, QDM) 与其诸多的衍生变体，如我们后面会提到的量子回路模型（quantum loop model, QLM）。这些模型往往是用关联电子和阻挫磁体中提炼出的系统的低能有效自由度写下的，如 QDM 其实就是把著名的 P. W. Anderson 提出的共振价键（resonance valence bond）的图像用一种简化的方式写在晶格上。但与普通关联电子系统晶格模型不同的是，QDM 和 QLM 要求在晶格，如正方晶格（square lattice）、三角晶格（triangular lattice）、六角晶格（honeycomb lattice）、笼目晶格（kagome lattice）等等的格点上，有且仅有一个dimer（对于 QDM来说）或者两个 dimer（对于QLM来说）。这有且仅有就使得 QDM 和 QLM 比普通的多体模型多了一个局域几何限制条件（local geometrical constraint），并使得系统的 Hilbert空间，虽然仍然是随着系统的尺寸指数地增大，但受到 Hamiltonian 层次之外的局域限制。

正是因为存在局域几何限制，受限量子多体系统的数值求解变得十分繁琐。在传统求解自旋系统的量子蒙特卡洛方法中，不管是路径积分的蠕虫（worm）算法，还是 SSE 的圈（loop） 更新方法，都不用考虑局域约束条件，算法只需要满足模型的全局对称性或者全局约束条件——如总自旋守恒或者总粒子数守恒——就行。也就是说，自旋的翻转与否和周边的自旋构型无关。但是QDM/QLM中因为被施加局域几何限制条件，晶格中的每个 link 有两个状态：有 dimer 或没有 dimer。如果此时只是翻转单个 link 的状态，即从占据变成不占据或者反之，则会破坏每个格点有且仅有一个 dimer 的约束条件。所以在每次蒙特卡洛更新的时候都要检查是否违反了这一局域约束条件。这就是问题的难处，在数值模拟时不光要在指数相空间中做高效更新，还得在每次更新时遵守局域约束条件，这就好比人要带着手铐和脚镣跳舞，受尽束缚，一如胡适的、还有我们所有人的不自由的人生，和我们在限制中的努力挣扎。

所幸的是，就算受尽束缚，人们也还是发展出初步解决受限量子多体问题的蒙特卡洛算法。笔者和少侠严正博士在之前的文章中[4]，专门介绍过严少侠开发出的扫描团簇量子蒙特卡洛算法[5]。它能够在路径积分的框架之下通过扫描团簇的更新方式，以代数的计算复杂度遍历 QDM /QLM的满足局域限制条件但仍是指数复杂度的相空间，得到受限量子多体系统的统计性质，从多体计算的技术上初步解决了受限量子多体问题的模拟难题。我们在三角晶格 QDM 的扫描团簇量子蒙特卡洛模拟中取得了关于系统动力学行为的初步成果[6]。对于计算技术感兴趣的读者，可以翻看参考文献[4, 5, 6]。本篇文章将要介绍的，是我们把不自由的人生推到更加困难的境地——三角晶格量子环路模型——并从中发现新的物理学现象的故事[1]。

三三角晶格量子环路模型相图

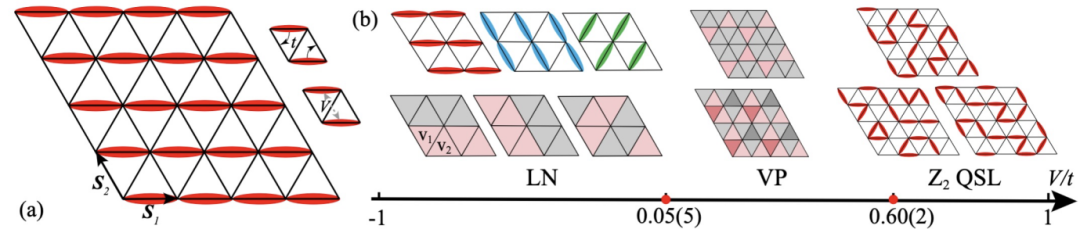
图1. (a) 三角晶格量子环路模型（quantum loop model）中的一种 dimer 排列方式。这样的方式就是 lattice nematic (LN) 相列固体相，每个格点上 dimer 手拉手满足 QLM 每个格点上有两个 dimer 的局域约束条件，同时形成满足晶格平移不变性的相列相。如此的相列相整体旋转60度或者120度，仍是 LN ，故 LN 三重简并。右上角两个小图，是 QLM 系统 Hamiltonian 中的动能 t 项和势能 V 项。(b)下方是计算所得的相图，随着 V/t 从负到正，系统从 LN 相经过 vison plaquette (VP) 固体相，到达 Z2 量子自旋液体 (Z2 quantum spin liqud, Z2 QSL) 相。其中 VP 固体相就是我们发现的 hidden phase，解决了之前工作中争论。而 LN-VP 的1级相变和 VP-QSL 的连续相变，都和3维 O(3) 各项异性模型的相变过程吻合，与共形场论 Bootstrap 对于该模型的最新结论一致。上方的小图，是LN, VP 和 QSL 相中，dimer与 vison 的排布方式。

我们这里研究的是三角晶格量子环路模型，如图1（a）所示，三角晶格的每个格点上有且仅有两个 dimer，这就是QLM的局域约束条件，而系统Hamiltonian 中的 dimer 翻转动能项 t 与势能项 V 在满足局域约束条件的情况下互相竞争，V/t 取不同的值时，得到不同的量子基态 dimer 排布方式，即不同的相。这个模型的基态相图十多年来一直存在争议，如比较有代表性的文献[7, 8]都研究了这个问题。这两篇对于模型的在极限参数条件下的相都没有疑义，如 dimer 吸引相互作用很强（就是 V/t <0 的时候）的时候是 lattice nematic (LN) 相列固体相，就是图1（a）中红色 dimer 手拉手排起来的样子，而且因为三角的晶格的三度旋转对称性，LN 有三种简并的排法（也就是图1(a)中所示的，图中的旋转60度以及旋转120度的三种情况）；而当 dimer 的动能 t 和排斥相互作用 V 相等的时候（就是 V/t=1），也就是著名的 Rokhsar-Kivelson point，系统处在一个自旋液体状态，并且由于三角晶格是不可二分晶格，此处的自旋液体会向着 LN 相的方向延展，变成具有  Z2 拓扑序和分数化 vison 任意子元激发的奇异量子物态。然后随着 V/t 参数向着 LN 方向调节，vison 任意子最终会发生凝聚（condensation）使系统从 Z2 QSL 进入固体相。如是的任意子 condensation 现象，及其所伴随的对称性分数化和疏运行为的分数化与物理观测，都是目前领域内的研究热点，笔者在之前的介绍中亦都有提及，感兴趣的读者可以参看文献[4, 9]。

但此处的问题恰恰就是，Z2 QSL能够延展到什么参数范围？这方面10多年来物理学家们进行了很多的尝试，但是仍然没有明确的答案。以图1（b）下部的 V/t 相图上的刻度来说，文献[7]通过进行小 size 的严格对角化计算，认为 LN 到 Z2 QSL 之间是一个叫 O(3)* 的连续相变，相变点在V/t = -0.3 左右。对于这个相变的理解来源于 vison 构成的 LN 相的序参量在相变点处产生涌现连续O(3) 对称性，而 O(3) 后面的 * 是因为此处 vison 作为分数化激发，给了相变一个很大的反常维度，但文献[7]的结果受制于强烈的有限尺度效应，与热力学极限的实际情况相差甚远；而文献[8]通过进行近似的蒙特卡洛模拟，得到比文献[7]稍微精确一些的结果，他们虽然也认为 LN 到 Z2 QSL 经过一个连续相变，但是相变点不在 -0.3 而是起码在 0.7 处，而且他们还发现，大概 V/t 从 0 到 0.7 , LN 相的 O(3) 序参量是接近于0地小，也就是说，他们觉得从文献[7]所说的 -0.3 到他们所发现的 0.7 之间，系统 LN的序参量好像为零，也许有其他的相存在。但是可惜文献[8]由于彼时算法和作者们想象力的限制，只是看到了问题的苗头，却没有能够找到正确的解答。

我们在文章[1]中的发现就是，图1（b）的V/t 相图中，在 0 和 0.6 之间的确存在着一个新的之前大家没有见过的量子物相。这个相破缺三角晶格的平移对称性，如图1（b）中间标记 VP 之上的小图所示，但是平移对称性的破缺不在 dimer 的构型中体现，也就是说这里测量 dimer 关联无法看到有序，所以对于dimer 来说此相是隐藏起来的 hidden phase，而找到它真正需要测量的是系统中涌现出来的 vison 关联。这样的序是 vison 形成的 plaquette 固体, 我们把它称为 vison plaquette (VP) 相。相图中Z2 QSL 向着 LN 走的时候，vison 任意子凝聚所形成的固体相，就是这样一个 hidden phase，而不是文献[7, 8]中所认为的 LN 相。这样的 hidden phase 大家之前都没有见过，也难怪文献[7, 8]中几位领域内的行家里手，虽然做了努力，也没有能够窥其堂奥了。

那么该如何理解从 Z2 QSL 到 VP 再到 LN 这样完整的相变过程呢？让笔者颇为惊奇的是，此事和共形场论 Bootstrap 研究进展建立起了联系，需要借鉴 Bootstrap 的他山之石才能获得完整的解答。文章[1]合作者中，有一位少侠荣俊臣博士，将这样进展教给了大家。原来一直以来，在统计物理和高能物理研究中，大家对于3维 O(3) 相变对于 cubic 各项异性的稳定与否，一直存在争议。也就是说，在如下公式所示的拉格朗日量中，

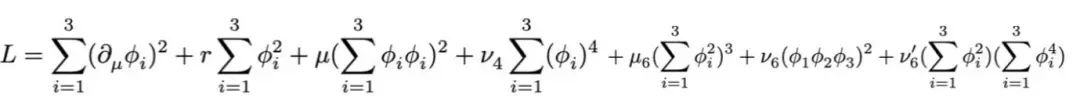
O(3) 序参量（phi1, phi2, phi3）在各项异性项诸多系数 nu4, mu6, nu6, nu6’都为0时，能够实现3维 O(3) 相变——海森堡模型仍是海森堡模型；但是如果诸多各向异性项不为0，这些系数能否在重整化流中，能否再流回它们为0非干涉（irrelevant）情况而使体系重回 O(3) 不动点 (fixed point) ？这个问题从1970年代一直讨论到今天，才刚刚有一个满意的回答。

其实前面提到的文献[7]中的基本假设就是各向异性项是非干涉的，所以从 Z2 QSL 到 LN 的O(3)* 相变可以发生，但这个假设笔者和合作者几年前在一个有效模型中给出了一个否定的回答[10]。最近几年共形场论 Bootstrap 计算的迅速发展，对于上面说到的3维 O(3) 相变对于各项异性的不稳定性问题，刚刚给出比较完整的回答[11]（这篇文章中的少侠苏宁博士，也和少侠荣博士一道，教给我们很多共形场论 Bootstrap 领域的新知识）。笔者用磕磕绊绊的语言大概描述一下：诸多各项异性项中，最重要的 nu4, 当 nu4>0 的时候，O(3) 相变是不稳定的，重整化流会将系统带到一个3维 Cubic 不动点；也就是说，此时系统的相变虽然仍是连续相变，但普适类已不再是 O(3) 海森堡，而是 Cubic；而当 nu4 从 大于0 变化到小于 0 的过程中，系统会经历一个一级相变，而O(3) 序参量（phi1, phi2, phi3）在其三维相空间中的分布，会从 nu4 > 0 时位于一个序参量空间立方体的8个顶点变成 nu4 < 0 时位于序参量空间立方体的6个面心。

那么这样看似抽象的描述，在我们的 QLM 模型的计算中具体是如何体现的呢？其实上面拉氏量中的 O(3) 序参量我们可以通过蒙特卡洛模拟中的 dimer 构型读出，读出的方式大概就是图1 (b) 中标记 LN 和 VP 处，上面一行 dimer 构型和下面一行 vison 构型的对应方式。对于每个蒙卡 dimer 构型，可以按照如下公式给出 O(3) 序参量的三个分量，

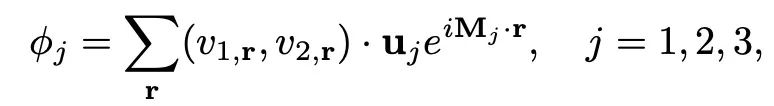
此处 r 遍历三角晶格，（v1, r，v2, r）就是三角晶格每个平行四边形中 vison 所在的 1，2两套子格，矢量 uj 体现三角晶格的三重旋转操作，而动量 Mj 是布里渊区中的 M 点，是 LN 相中对应的 vison order wave vector。如此的构造，可以让我们通过蒙特卡洛的抽样过程，直接得到上面拉氏量中的各向异性项系数与伴随的 O(3) 序参量在3维相空间中的分布函数，也就是说，我们可以在 V/t 的相图上，通过蒙卡模拟直接验证上面所说的共形场论 Bootstrap 得到的对应 O(3) 到 Cubic fixed point 的重整化流的流动过程。

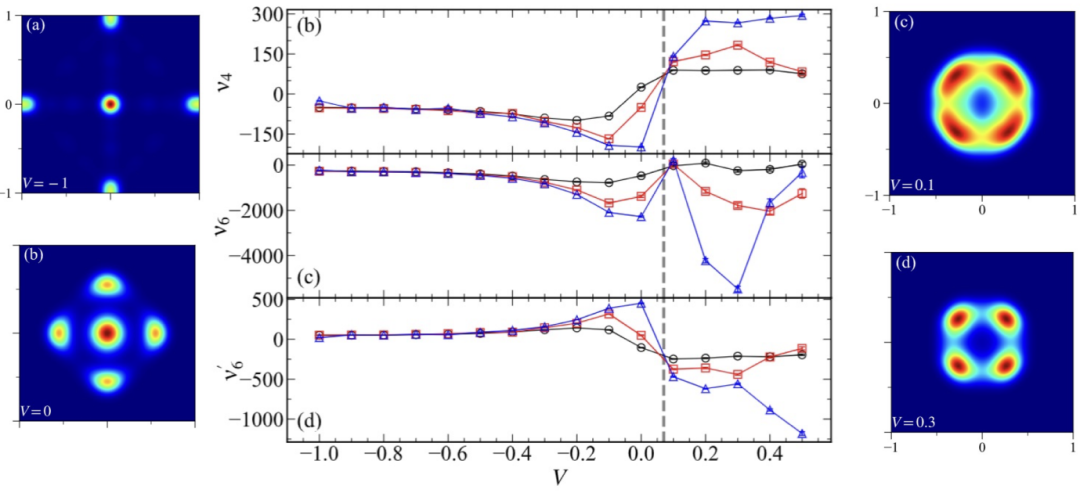
图2. 左为 QLM O(3) 序参量的在 LN 固体相中的分布，亮点位于序参量相空间立方体的前后左右上下6个面心，此处将序参量分布从3维投影到2维；右为 QLM O(3) 序参量在 VP 固体相中的分布，亮点位于序参量相空间立方体的8个顶点上，此处也将序参量分布从3维投影到2维。中间是蒙特卡洛计算所得的相变过程中各项异性项的系数，nu4 在从 LN 到 VP 的1级相变处 V/t =0.05(5) 从负变到正，与 histogram 的表现一致。

图2中所示的，就是三角晶格 QLM 模型中，从 LN 到 VP 1级相变过程中蒙卡计算所得 O(3) 序参量的分布函数和拉氏量中的各项异性项系数。尤其值得注意的是，nu4在V/t 从小于0到大于0的调节过程中（三条线代表三种不同的晶格尺寸），确实从负值变成了正值。与之伴随的，序参量的分布函数 (histogram)，在 nu4 图的左边， V/t=-1 和0 的时候，明显分布在立方体的6个面心上（注意此处我们将3维序参量空间投影到2维，所以原点处的亮点实际上是前后两个面的面心）；而在nu4 图的右边，V/t=0.1 和0.3 的时候，序参量的分布经历1级相变突然转移到了立方体的8个顶点（仍然需要注意此处是将3维序参量空间投影到2维，所以每个亮点其实是序参量立方体前后两个面上的亮点）。这样的1级相变发生在 V/t=0.05(5)，正是文献[8]发现 LN 相实际上几乎消失的地方。

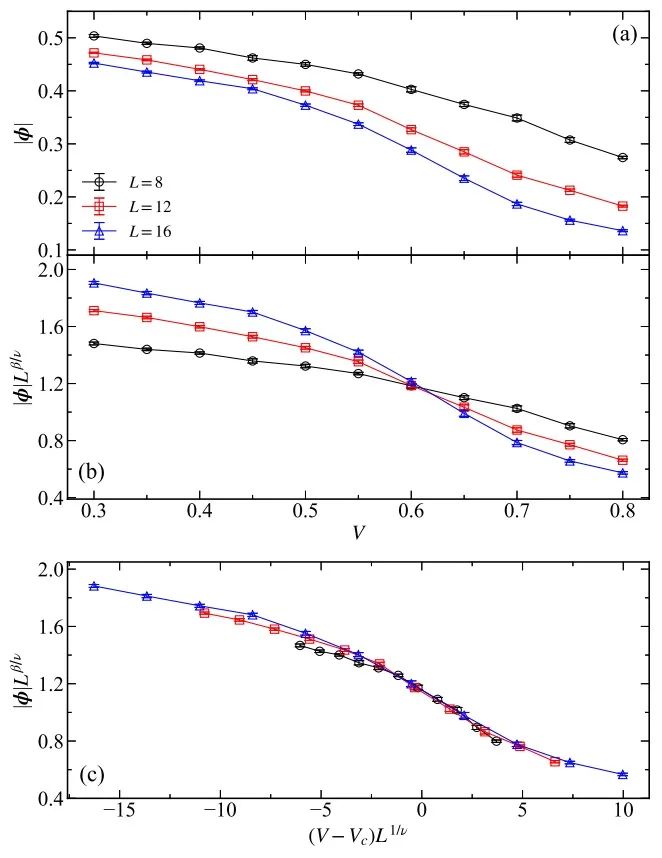
图3. (a) 为从VP 固体相到 Z2 量子自旋液体相的连续相变过程中，vison O(3) 序参量的变化过程。(b), (c) 为通过 3维 O(3) 临界指数，对于序参量数据进行的数据跌落分析，可以看到预期的 vison condensation 临界行为。

有了这样的结果，我们终于明白之前文献中互相矛盾和没有把问题说清楚的地方，其实有些共同的原因：首先是工具层面的，之前的研究中还没有能够克服受限系统计算问题的扫描团簇蒙特卡洛算法；其次是观察角度的问题，之前的研究中没有意识到 VP 相作为 hidden phase 不应该在 dimer 的构型而需要在 vison 关联中寻找；最后是对于QLM 低能有效理论理解的问题，之前工作仍然误以为各项异性项对于 O(3) 相变是非干涉的微扰。在量子多体物理学研究中，这些从工具到概念的困难其实是普遍存在的，解释和解决新的物理问题，总是需要克服这样的困难，而且克服它们也不可能一蹴而就，需要从业人员长时间的积累、研究工具的改进以及借鉴本领域和其他领域的最新进展。但是，同样重要和需要的，不正是发扬如胡适一般的青年气魄，在限制中找到新天地的精神么？

最后一点关于物理的篇幅，讨论从 VP 到 Z2 量子自旋液体的 vison condensation 连续相变。前面已经说过，最新的共形场论 Bootstrap 结果告诉我们，因为 VP 相的拉氏量具有不为0的各向异性项，mu4>0，此处的连续相变是3维 Cubic* 普适类，而不是3维 O(3)* 普适类。但是Bootstrap 的结果也告诉我们，这两个普适类关于临界指数的差别，在小数点之后4位或者5位（这也是从1970年代到今天，大家无法区分他们的差别的原因），对于我们所能够模拟的有限尺度晶格 (最大尺度为16 x16 的三角晶格)，这样临界指数的差别是无法感受到的，所以我们可以放心的使用已知的3维 O(3) 相变的临界指数对于图3 (a) 中的序参量原始数据进行图3 (b), (c) 有限尺度标度分析，分析的结果就是图3 (c) 中三个不同尺度的蒙卡数据，可以看到在 Cubic* 临界点 V/t=0.60(2) 的附近，三个不同尺寸的数据完好地落到了普适的标度曲线上，这就是 VP 到 Z2 拓扑序 QSL vison condensation 量子临界点的有力数值证据。

最后，文章[1]中还讨论了还有很多有趣的物理细节。比如如何通过对比严格对角化和蒙特卡洛计算证实 VP 相在 dimer 的角度确实是一个 hidden phase；比如这样的 hidden phase 如何在 dimer 的非对角测量中看到并对理德堡原子实验中发现的新奇物相有什么理论上的借鉴意义；比如 3维O(3) 相变中各项异性的分析对于过渡金属二硫化物材料中的结构相变有什么新的建议等等。读者诸君如果感兴趣，可以参看原文 [1] 或者求诸文章作者中的冉晓雪少女侠、严正博士少侠、王艳成博士少侠、Rhine Samajdar 博士少侠、荣俊臣博士少侠、戚扬教授和 Subir Sachdev 教授师徒二位大侠。相信 她 / 他们中的每位都会与您分享对于这项工作的理解，不负各位看官的期待。

四回望胡博士

笔者还能再说几句的，就是回到文章开头的胡适。“情愿不自由，便是自由了”，一如胡博士，我们的人生都有太多的约束和限制，如何才能在不自由的生活中不断寻找自由的寄托，努力创造新的生活和事业，以青年人应有的乐观态度在自己的领域中创造出无愧于心的作品，这是我们每人都要面对的人生课题。生活的磨砺，环境的摧残之下，到底是妥协放弃还是就算戴着手铐脚镣，也要“用代数计算复杂度克服指数相空间”，也要尽可能地自由探索冲出生活为我们预设的条条框框，也许还是可以选择的。再把眼光拉长一些，从胡适、鲁迅的年代到今天，一百年过去了，他们提出的问题，对我们来说其实仍然需要面对，再抄一段胡博士的大实话，与读者诸君共勉：

“争你们个人的自由，便是为国家争自由！

争你们自己的人格，便是为国家争人格！

自由平等的国家，不是一群奴才建造得起来的！”

参考文献

[1] Fully packed quantum loop model on the triangular lattice: Hidden vison plaquette phase and cubic phase transitions

Zheng Yan, Xiaoxue Ran, Yan-Cheng Wang, Rhine Samajdar, Junchen Rong, Subir Sachdev, Yang Qi, Zi Yang Meng

arXiv:2205.04472

[2] Quantum simulation of 2D antiferromagnets with hundreds of Rydberg atoms

Scholl, P., Schuler, M., Williams, H.J.et al.

Nature 595,233-238 (2021).

[3] Probing topological spin liquids on a programmable quantum simulator,

Semeghini G., Levine H., Keesling A. et al.

Science 374, 1242-1247 (2021)

[4] 瞧！这些发明算法的人

严正，孟子杨

量子材料Quantum Materials, 2021/04/16

[5] Global scheme of sweeping cluster algorithm to overcome the topology localization

Zheng Yan

arXiv:2011.08457 (2020)

[6] Topological phase transition and single/multi anyon dynamics of Z2 spin liquid

Zheng Yan, Yan-Cheng Wang, Nvsen Ma, Yang Qi, Zi Yang Meng

npj Quantum Materials 6, 39 (2021)

[7]  Z2 topological liquid of hard-core bosons on a kagome lattice at 1/3 filling

K. Roychowdhury, S. Bhattacharjee, and F. Pollmann

Phys. Rev. B 92, 075141 (2015)

[8]  Magnetization plateaus of an easy-axis kagome antiferromagnet with extended interactions

X. Plat, F. Alet, S. Capponi, and K. Totsuka

Phys. Rev. B 92, 174402 (2015)

[9] 无愁河上的浪荡汉子们｜量子多体中的呐喊与彷徨之十一

孟子杨《物理》2021年第11期[10] 学好蒙特卡洛，不会被忽悠

孟子杨[11] Bootstrapping Heisenberg magnets and their cubic instability

Shai M. Chester, Walter Landry, Junyu Liu, David Poland, David Simmons-Duffin, Ning Su, and Alessandro Vichi

Phys. Rev. D 104, 105013 (2021)