前言 

生物统计学由于其中无法回避的数学内容，容易让非数理或统计学背景的制药业研发人员望而生畏。生存分析有三大支柱：(1) Kaplan-Meier曲线；(2) 对数秩检验 (Log Rank Test)；(3) Cox回归模型。其中方法(1)和(2)背后的概念和运算除了与条件概率有关的定义很难科普之外 (但可以诉诸直觉而绕过)，其余内容只需中学数学知识就能理解；方法(3)涉及的数学内容相对复杂，可能更适合读完本文后意犹未尽的读者通过教科书来自学。幸运的是，对于临床试验中常见的双样本分析而言 (也即比较试验组和对照组的两条生存曲线时不考虑其它协变量和分层分析)，对数秩方法既是给出差异显著性概率值的最常用手段，也能用来近似估算出与Cox回归法渐近等价 (asymptotically equivalent) 的风险比数值。

近年来中文出版界出现了包含数学公式的专业科普未必曲高和寡的可喜现象。在这些成功范例的鼓舞下，本文将从最基本的概念开始，对“生存分析海洋”的两大水域大胆进行深度潜水式科普。

撰文 | 徐亦迅

Robert Weinberg教授的“The Biology of Cancer”是癌症生物学领域不可多得的经典教科书，自2007年第一版发行以来，无数生物专业学生以及癌症研究人员从中获益。从2011年开始，CTLA-4抗体和PD-1抗体先后成功，令癌症免疫疗法名声大噪，在全球制药界变得炙手可热。Weinberg教授自然要在2013年的第二版中增加不少关于免疫哨卡抑制剂 (immune checkpoint inhibitors) 的内容，在解释FDA（美国食品药品监督管理局）为何批准CTLA-4抗体ipilimumab (商标名：Yervoy) 用于治疗已经扩散的黑色素瘤病人时，他写道：“试验组病人接受ipilimumab治疗后的中位总生存期是10个月，而对照组病人接受gp100多肽疫苗治疗后的中位总生存期是6个月”[1]。言下之意，这4个月的中位总生存期差异是FDA最后绿灯放行的关键。在这里，Weinberg教授对临床研究结果[2]的解读可谓“捡了芝麻，丢了西瓜”：他只关注了“横切”两条生存曲线后得到的中位总生存期的差异，而不知原文括号里的风险比 (HR = 0.66) 和概率值（P = 0.003）才是FDA专家委员会决策的更重要依据！要想真正理解Weinberg教授产生误读的原因，我们首先需要掌握生存分析的一些基本概念。

生存分析中的基本概念

生存分析 (survival analysis)

生存分析是一系列统计学方法的总称，用以分析研究者感兴趣的事件发生前的持续时间数据。生存分析的应用范围非常广泛，其中包括抗癌药物临床试验中的生存时间分析、工程学中的故障时间分析、计量经济学中的持续时间分析。

事件 (event)
 

事件的具体定义取决于新药试验中事先指定的临床终点 (clinical endpoint) 。如果终点是总体生存期 (overall survival, OS)，那么事件就是患者的死亡。如果终点是无进展生存期 (progression-free survival, PFS)，那么事件就是患者病情的进展 (例如固体瘤增大或者白血病的血液指标恶化) 或者死亡。生存分析能在生物医学以外的许多不同领域有用武之地[3]，其关键就在于事件这个概念在定义上的灵活性。

生存时间 (survival time)

指从病人被随机分派进入临床试验的分组 (相对的时间零点) 直到事件发生所经历的时间跨度。临床试验的病人招募通常是个持续的过程，不同病人的试验一般始于日历上不同的具体时间点，在数据分析时只有采用相对时间，才能有同样的时间轴及零点。对于一个临床试验的病人群体而言，个体病人的生存时间是一个随机变量，用大写的T表示。而生存曲线横坐标则对应各病人事件发生的时间点，它不是随机变量 (而用做函数的自变量)，用小写的t表示。随机变量T一般不遵从正态分布。

删失（censoring）

指由于事件没有被观测到或者无法观测到，而导致生存时间无法精确记录的情况。其中最为常见的情形称为右删失（right censoring，图1），对这样的病人我们只知道其生存时间要大于从试验开始到删失发生的时间。有多种原因可以导致右删失情况的出现，其中包括：(1)病人在某时间点上退出试验或失去随访信息；(2)病人在整个试验结束时事件还未发生；(3)病人由于毒性等原因停用被分派的药物或换用其它药物；(4)竞争风险事件的发生。

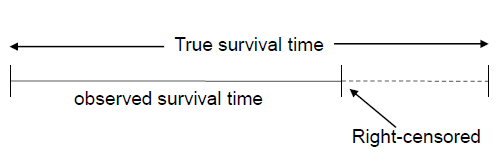
图1. 生存时间数据的右删失现象。
 

生存时间T的非正态分布以及删失情况的存在让传统的统计方法在分析这类数据时无用武之地，于是统计学家们殚精竭虑，直到1970年代才使生存分析这一方法体系趋于成熟。

生存函数 (survival function)
 

又叫累积生存概率（cumulative survival probability），其定义公式为S(t) = P(T > t)。该函数的意义就是生存时间大于时间点t的概率。显然当t = 0时，S(t) = 1，每个病人在各自的试验开始时都还没有事件发生。而随着t的增加，S(t)逐渐向0方向递减（严格来说是不增）。理论上的T和t一般是连续变量，相应的生存函数S(t)的图像就是一条光滑的曲线 (图2左)。而在临床试验的实践中，T只能在有限个不同的时间点t被观测到，因此我们常用不增的阶梯曲线来描述估测出的生存函数（图2右）。

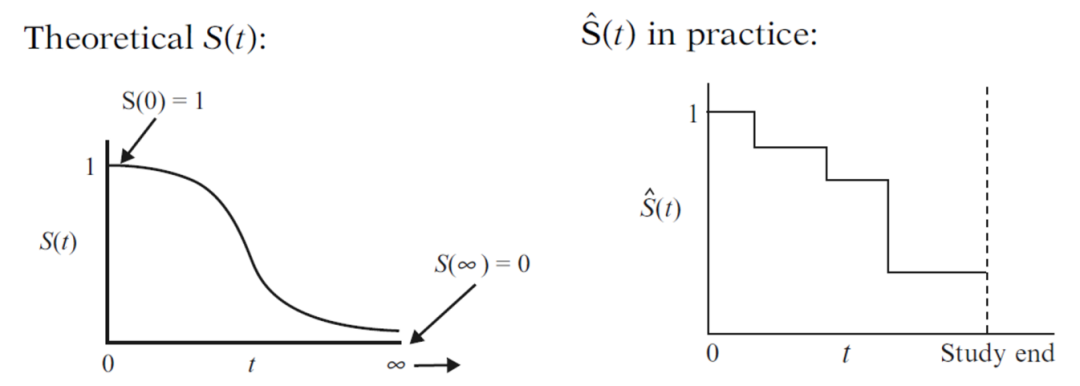图2.理论与实践中的生存函数。丨来源：Kleinbaum, D.G. & Klein, M. (2012) Survival Analysis: A Self-Learning Text, 3rd Edition。
 

图3可以帮助我们进一步理解光滑曲线和阶梯曲线之间的区别：红色数据点的纵坐标代表根据试验结果估算出的累积生存概率值，我们若想用光滑曲线来连接就需要对随机变量T的分布做出假设的参数拟合法，而曲线一般不宜正好经过所有的红点 (那样会导致过度拟合而使得统计模型没有多大效用) ；若用非参数的阶梯函数来连接，那么曲线简单而唯一确定！这一区别正是Kaplan-Meier非参数估计法能够成为生存分析领域一大支柱的关键。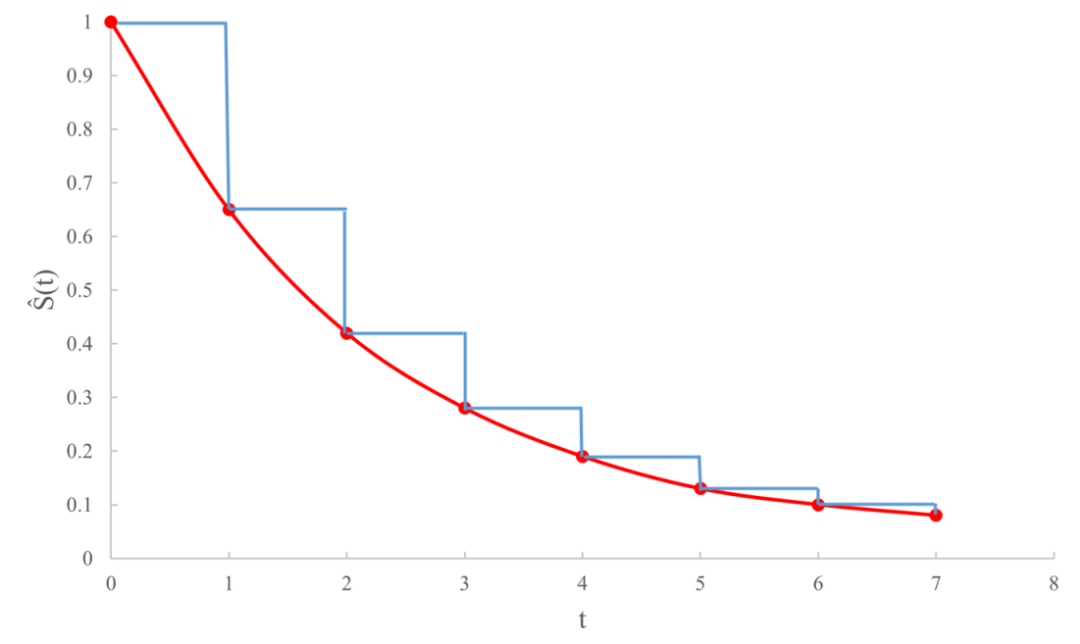
图3. 阶梯函数的使用可以改善光滑曲线估计生存函数的过拟合问题。

风险函数 (hazard function) 和风险比 (hazard ratio)

一个函数将自变量定义为时间，目的就是要研究因变量随时间的变化规律，也就离不开“变化率”这个重要概念，需要用到微分或差分的数学工具。生存函数S(t)描述的是组内尚未发生事件的累积病人比例，由于删失情况的存在，它与已发生事件的累积病人比例之间的数学关系不再简单。统计学家们通过实践发现，研究与病人发生事件的概率有关的风险函数能提取出更多蕴含在生存数据中的信息。

风险函数 (又称为风险率，hazard rate) 的直接数学定义需要用到条件概率和极限两种概念的组合，不是科普文章的最佳选择。不过该函数也可以通过生存函数S(t)来间接定义：

从定义式可以看出，h(t)基本就是S(t)对时间的导数除以S(t)。由于S(t)一般随时间递减，加上一个负号是可以让h(t)在取值上非负，从而在使用上更加方便。而h(t)在从零开始的一个时间段内的积分，H(t)，则被称为累积风险函数 (cumulative hazard function)：

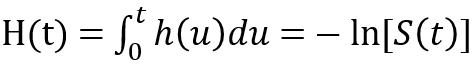
以上两个定义式为了简洁而假定时间t为连续变量，若t为离散变量时也有相对应的定义，我们只需记得微分的离散对应是差分，而积分的离散对应是求和。

在新药临床试验中，两条不同生存曲线的背后隐藏着两个不同的风险函数：h1(t)和h2(t)。统计学家们通过研究许多生存数据后发现，如果试验组和对照组病人的随机分派做得足够好， 我们在很多情况下就能用一个近似成立的比例风险假设 (proportional hazards) 来简化生存数据的分析：

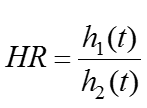
在这里我们假设被比较的两个风险函数之比率是一个不随时间变化的常数，用HR (hazard ratio，风险比) 来表示。制药业的常用惯例是：试验组的风险函数作为分子，而对照组的风险函数作为分母 [注意：某些论文和教科书可能会反过来]。如果试验组生存曲线总体在对照组之上，那么HR就在0到1之间取值，数值越小，两条曲线的差别就越大，也就意味着新药的相对疗效优势越大。需要指出的是，虽然生存分析中的常用方法无需比例风险假设严格成立，但是试验数据有时会有大幅度偏离该假设的情况，其统计分析就需要对本文所介绍的方法做一些在数学上比较复杂的改进，这已经超出了本文的讨论范围。

揭秘Kaplan-Meier曲线

可以毫不夸张地说，近几十年来发表的临床癌症学会议报告和期刊论文中，几乎每篇都至少要包含一幅Kaplan-Meier生存曲线图。没有统计学背景的新药研发人员在专家的指引下通过多看虽能大致明白生存曲线的含义，但是对其背后的简单运算往往有一种不必要的神秘感。而统计学家们赋予Kaplan-Meier法的专业术语“乘积极限估计” (product limit estimator) 更是让非专业人士望而却步。

若想揭开笼罩在Kaplan-Meier曲线上的神秘面纱，最佳途径似乎是“解剖麻雀法”：通过彻底展示一个非常简单实例的详细计算过程，我们就可以让非专业读者也能用手画出一条生存曲线。笔者在此改编了文献[4]中的一组只有10位病人的生存数据，用字母依次给病人编号后列表如下：
 

表1. 临床试验中的生存数据示例

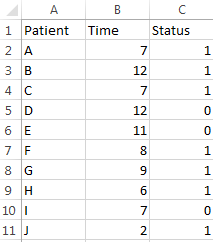
其中第二列是时间点t，以月为单位。而第三列的病人状态只有两种取值：0代表右删失，1代表死亡事件。整个试验持续的最长相对时间是12个月，期间10人中有7人发生死亡事件。病人I在第7月出现删失 (退出试验或失去随访)，我们对其生存时间的信息不完整，只知道大于7个月。而病人D在试验结束时依然存活。

要从表1估计出生存曲线，我们首先需将各行按照时间点t从小到大排序，记为ti，其中下标i表示序号。由于发生死亡事件与删失的离散时间点一般不是均匀分布，这些点把时间轴分割成了长短不一的区间，每个ti值代表了区间的起点。然后我们把每个区间里发生的死亡事件累加，记为di。若同时出现了死亡和删失，我们将用独立的两行来表示该区间。例如第7月就对应两个ti值：t3 = 7，t4 = 7+，其中的“+”号代表删失。每个区间起点时的存活病人数记为ni，那么在该时间段的存活比例 (surviving proportion) 就是：pi = (ni – di) / ni 。这样，我们通过整理和简单计算就得到了表2：
 

表2. Kaplan-Meier法估计生存函数的计算过程

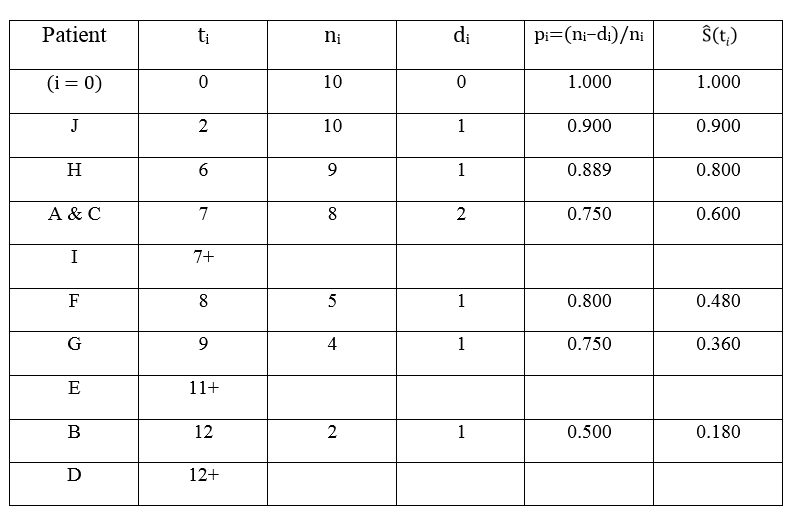
为了使读者概念更加清晰，笔者特地添加了第一行的时间零点。如果不存在删失，表2中每行的生存概率显然可以用一个简单的比值公式来估算：

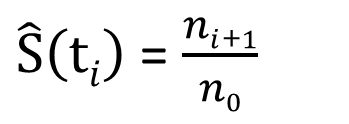
但是删失情况的出现会给这个思路带来困难。例如第8月结束时，病人F的死亡让组内存活人数下降为4人，用4 / 10 = 0.4来估算该时间段的生存概率显然不合理，它把第7月病人I的删失计为死亡，因此这里的0.4在统计学上被称为有偏估计量 (biased estimator) 。

要想找到生存概率的无偏估计量 (unbiased estimator) 并非易事。Paul Meier和Edward Kaplan这两个普林斯顿大学数学系博士生在1940年代末跟随同一位导师(统计学巨匠John Tukey)，而且同在1951年完成博士论文答辩，两人在校期间居然互不相识[5]。毕业离校各奔东西后，他们又在互不知晓的情况下独立研究了同样的问题，却殊途同归地找到了类似答案。最后在Tukey教授和期刊编辑的协调下，花了4年左右的时间才将两篇风格迥异的手稿整合成一篇论文[6]，著名的Kaplan-Meier乘积极限法终于在难产后诞生。此文问世半个多世纪以来，累计引用次数已经超过6万，这个数字在任何一个自然科学领域都是惊人的！

Kaplan和Meier基于条件概率的概念，经过一番并不简单的数学推导和探索，发现表2中pi的连乘积作为生存概率 S(t) 的非参数估计非常合适：

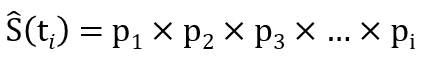
需要注意的是，出现删失的时间点没有对应的pi值，这些项也就自动被排除在算式之外 (本例中的p4, p7, p9都不存在)。这个无偏估计生存概率的连乘积公式，可以通过一个类比来获得直觉上的理解：很多电子游戏都采用序列冲关的设计，游戏者只有先“活过”前面每一关，才能到达目前要闯的这一关。这其实就是条件概率连乘的思路，与物理学中串联电路的乘法原理也一脉相通。因此所谓“乘积极限法”其实一点也不神秘。现在我们可用该公式来重新估算第8月时间段的生存概率：

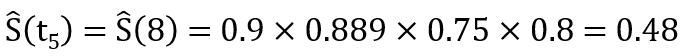
0.48这个数值显然比把在前一时间段发生删失的病人I计为死亡而得出的0.4更为合理 (也要比把病人I当成肯定在第8月依然存活的有偏估计值0.5更合理) 。通过Kaplan-Meier法计算出的各时间段内生存概率值放在表2的最右一列，然后将这些数值作为相应区间的纵坐标对时间作图，就可得到下面的生存曲线：

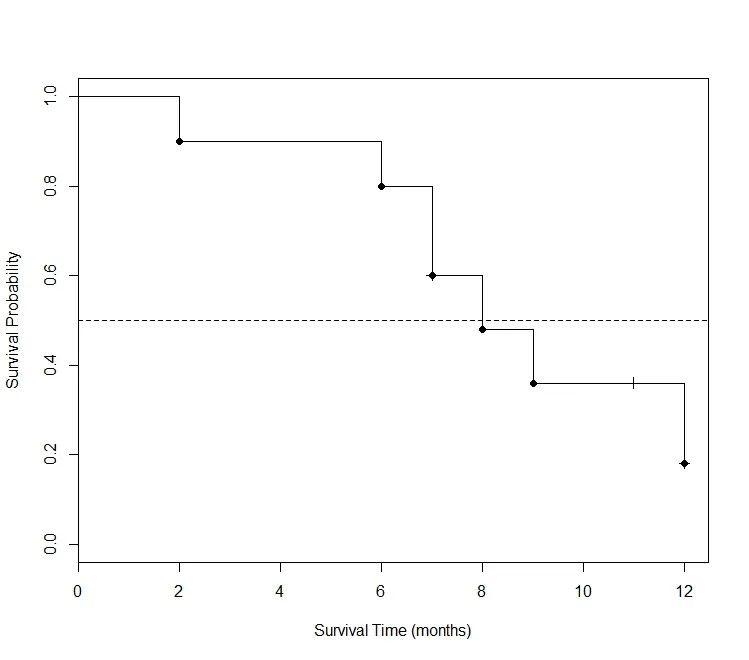
图4. 由表1数据计算得出的Kaplan-Meier生存曲线。
 

图4只有6个数据点，有兴趣的读者完全可以用手工来完成。不过用专业软件来画 (例如本文使用的R语言) 可以更方便地在图中添加注解性内容，例如在纵坐标为0.5处用一条水平线来就横切该曲线，就发现本试验组的中位生存期为8个月。

通过研究这个只有10位病人的简单实例，没有统计学背景的读者跟随笔者一路走来，或许也能对Kaplan-Meier曲线有“会心不远”的感觉。

统计学中的假设检验

对于新药的临床试验而言，最重要的问题显然是比较试验组和对照组这两条生存曲线的差异：曲线分开的程度以及相应的统计显著性。衡量统计显著性的常用方法是对数秩检验，这个命名起源于非常晦涩的等价数学推导[7]，我们在实际应用中根本不会感觉到“对数”和“秩”的存在。一个更好的名称也许是Mantel检验，可惜文献中的习惯一旦形成就很难更改。
 

用概率值来度量显著性是基础统计学的核心支柱之一，其标准名称为假设检验(hypothesis testing)，这是一个几乎人人有所耳闻却又经常被误解的论题。统计学界内部都没能统一思想，在假设检验如何操作上分为两大流派：Fisher流派是大多数教科书中的主流，但是Neyman-Pearson流派的影响也不容忽视。如何正确理解假设检验是大多数非统计学背景的读者在自学中需要跨越的路障之一。2016年3月，英国著名的《Nature》杂志发表了一篇点击率很高的新闻报道，其中传达的重要信息发人深省：美国统计学协会对多年来科学文献中存在的大量对检验概率值的误用和滥用深表担忧[8]。

一言以蔽之，假设检验就是一个统计推断过程，它能基于样本数据 (sample) 而在两个相互对立的描述总体 (population) 特性的论断中做出合理选择。其中一个我们称为零假设 (null hypothesis)，而与它对立的就称为备择假设 (alternative hypothesis)。零假设的设立原则可以通过与一个现实生活实例的类比来说明：刑事诉讼中的无罪推定原则。刑事法庭的“零假设”就是被告无罪，只有在公诉方取得足够的可靠证据 (“样本数据”) 可以超越合理怀疑 (“统计显著性阈值”) 之后，审判方才能采纳被告有罪这一“备择假设”。两个对立的假设确定后，我们还需找到一个可从观测数据推算的统计量（test statistic），其零分布（就是在零假设成立前提下的概率分布）是已知的，从而计算出得到该统计量比从来自样本的观测值更极端的概率值。如果概率值小于事先约定的显著性阈值（比如常用的0.05），我们就拒绝零假设而接受备择假设；而若概率值大于显著性阈值，我们就无法拒绝零假设。值得注意的是，当零假设不能被拒绝时，我们并不能证明零假设成立！另外概率值越小虽然说明统计显著性越强，但它并不能用来描述两组之间的差异大小，这是由于概率值还依赖于样本量。若对这两个概念要点没有深刻领悟，非统计学专业背景的研究人员在陈述实验结果时就容易出错。

孟德尔遗传学中的拟合优度检验

生存分析中的对数秩检验属于经典统计学中著名的卡方拟合优度检验 (chi-squared goodness-of-fit test) 范畴，而拟合优度检验在生物学领域最著名的例子就是统计学泰斗Ronald Fisher将其用于分析孟德尔 (Gregor Mendel) 的遗传学实验数据[9]。

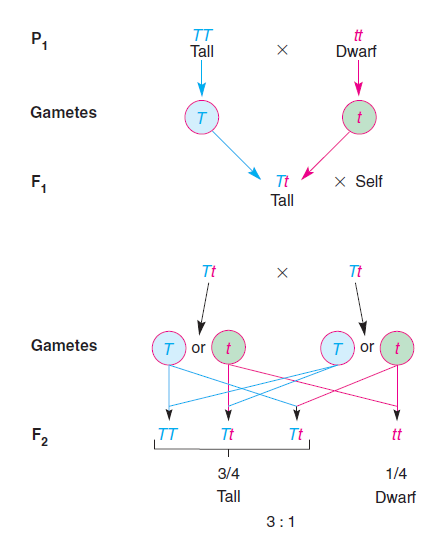
图5. 孟德尔根据豌豆杂交实验提出的性状分离理论[9]

图5展示了孟德尔根据豌豆杂交实验结果提出的性状分离假设。他在该实验中用了两个不同性状的亲代植株 (P1)：父本是高豌豆株 (基因型记为TT)，母本是矮豌豆株 (基因型记为tt)，其中高性状的等位基因T对于矮性状的等位基因t显性。基于孟德尔假设的理论推测是：子一代 (F1) 自花受粉后得到的子二代 (F2) 表现型将呈现3:1的分离。但是生命现象内在的随机性需要我们用概率论的视角来看问题，实验结果一般会和理论预期的3:1有一定的差异。孟德尔有一次实验后得到的子二代中有787株为高，277株为矮，观测到的比值为2.84:1。我们可以通过拟合优度检验来判断实测的高株数和矮株数是否与孟德尔假设相容 (注意：卡方拟合优度检验只能用于计数数据，而不能用于非整数的比值数据) ，这里两条对立的假设分别是：

• 零假设(H0)：观测到的高矮株计数符合理论预期的3:1比例；
• 备择假设(H1)：观测到的高矮株计数不符合理论预期3:1比例。

要定义合适的统计量绝非易事，近代统计学先驱Karl Pearson经过一番探索，率先在1900年找到了著名的拟合优度统计量，其定义公式为：

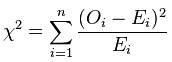
其中Oi代表观测到的高和矮两类 (n=2) 性状计数，Ei代表理论预期的两类性状计数。该统计量在零假设前提下的精确概率分布很难确定，好在样本足够大时非常接近著名的卡方分布 (chi-squared distribution) 。卡方分布曲线的形状还取决于自由度 (degrees of freedom) ，这个重要概念在很多教科书中都没有透彻的解释。本文也只能做简要讲解，有兴趣深入钻研的读者可以参阅文献[10]。概率论告诉我们，k个标准正态分布的独立随机变量之平方和遵循自由度为k的卡方分布。卡方统计量是一个由多个平方和累加而得的非负实数，总类数n越大，相应的项数也越多而导致统计量数值增大。由类数变多引起的统计量增值显然与假设检验的显著性无关，因此我们有必要对卡方统计量的分布曲线按照n的大小细分。在本文涉及的拟合优度检验和对数秩检验中，自由度都是k = n – 1。孟德尔实验中的n为2，因此其检验统计量的近似分布就是图6中自由度为1的棕黄色曲线：

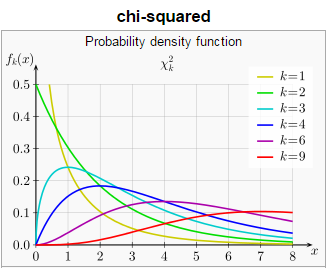
图6. 不同自由度下卡方分布的概率密度曲线。丨来源：Wikipedia

根据上述公式，我们可以基于孟德尔的实验数据通过下表来计算拟合优度检验所需的统计量：

表3. 根据孟德尔豌豆杂交实验数据推算的统计量

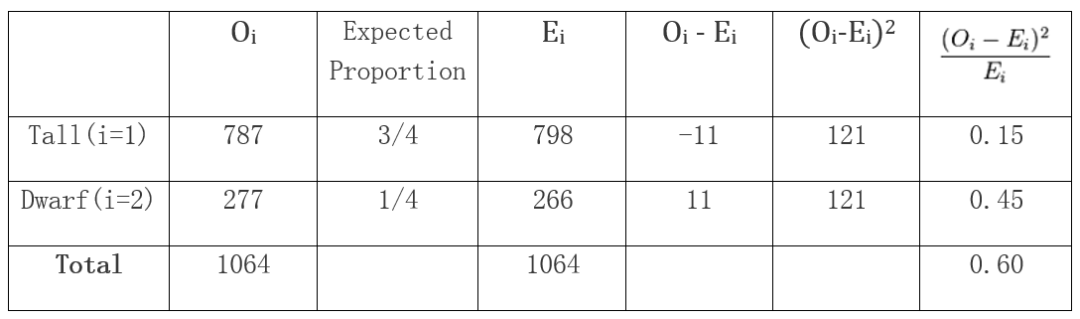
表3中的798和266分别是总数1064的3/4和1/4，也就是理论预期值 (Ei)。最后我们得到的统计量数值为0.60。通过查阅自由度为1时的卡方分布累积概率表，我们知道对应于概率值p=0.05的统计量数值为3.841。0.60要比3.841小很多，这意味着拟合优度检验的概率值要远大于0.05 (用一条简单的R语言代码可以算出p=0.439)，因此我们无法拒绝零假设，而认为孟德尔的实验数据与他理论预期的3:1分离比例相容。需要再次强调的是，实验数据与零假设的相容性并不足以证明零假设本身。

比较两条生存曲线

以上对孟德尔遗传学中的拟合优度检验之回顾将有助于我们深度理解对数秩检验何以能确定两条生存曲线差异的统计显著性。我们将通过一个来自文献[11]的实例来阐明对数秩统计量的计算过程。这是一个总共54位病人的急性淋巴性白血病 (acute lymphoblastic leukemia，ALL) 临床试验，目的是比较异体 (allogenic) 骨髓移植和自体 (autologous) 骨髓移植这两种疗法的差异。对ALL的一线治疗需要高强度的化疗和放疗，但这同时也会损伤成年患者的骨髓造血系统。很多ALL病人在一线治疗后还需要通过骨髓移植来修复造血功能和免疫系统。最理想的骨髓来自配型成功的病人亲属，这种异体骨髓移植的预后效果最佳。若病人没有合适的异体骨髓来源，就只能退而求其次，将病人自身的骨髓抽出体外进行药物处理，在杀灭ALL恶性细胞后再移植回病人体内。临床实践表明，在自体骨髓移植过程中，恶性细胞很难被消灭干净，因此其预后效果一般不如异体移植。我们对该临床试验的结果用上一节介绍的时间点排序后，整理成下面的表格：

表4. 急性淋巴性白血病临床试验的生存数据[11, 4]

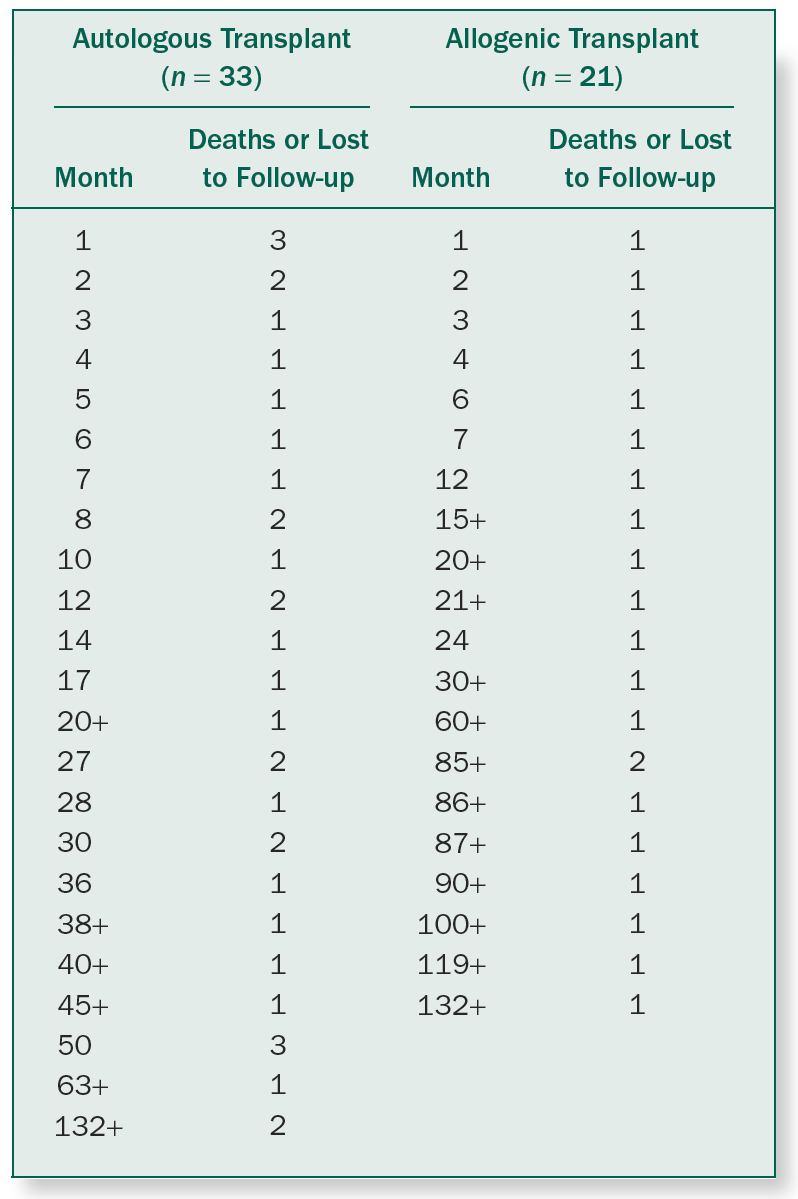
我们对这些数据进行前文已经介绍过的Kaplan-Meier乘积极限运算，就可画出这样两条生存曲线：

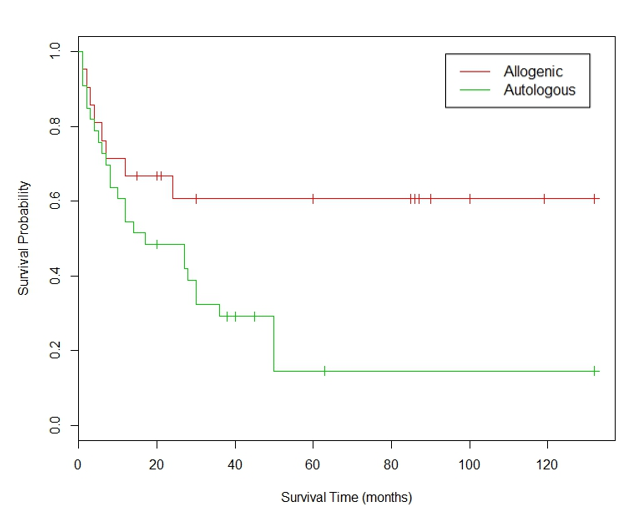
图7. 通过对表4数据计算得出的Kaplan-Meier生存曲线。
 

从图7可以看出，接受异体骨髓移植的ALL病人生存状况要明显好于自体骨髓移植。但是这个试验的样本不大，随机取样引起的波动依然可以让我们对两条生存曲线差异的显著性存疑。对数秩检验可以帮助我们来定量统计显著性，它的零假设是：两条生存曲线代表的病人群体在任意时间点上的生存概率没有差别。与零假设对立的备择假设无需赘述。需要特别指出的是：与Cox回归模型一样，对数秩检验也依赖于比例风险假设的近似成立。

对数秩检验的统计量与前述卡方拟合优度统计量在概念上颇有相似之处，只是由于删失数据点的存在，其计算过程要相对复杂一些。与Kaplan-Meier曲线的计算相似，第一步也是将两组病人发生死亡事件的各时间点t从小到大排序，每个ti值代表时段的起点。我们用A代表自体骨髓移植，用B代表异体骨髓移植，并将表4重新整理以清晰呈现详细的计算过程：

表5. 对表4生存数据进行对数秩检验的计算过程

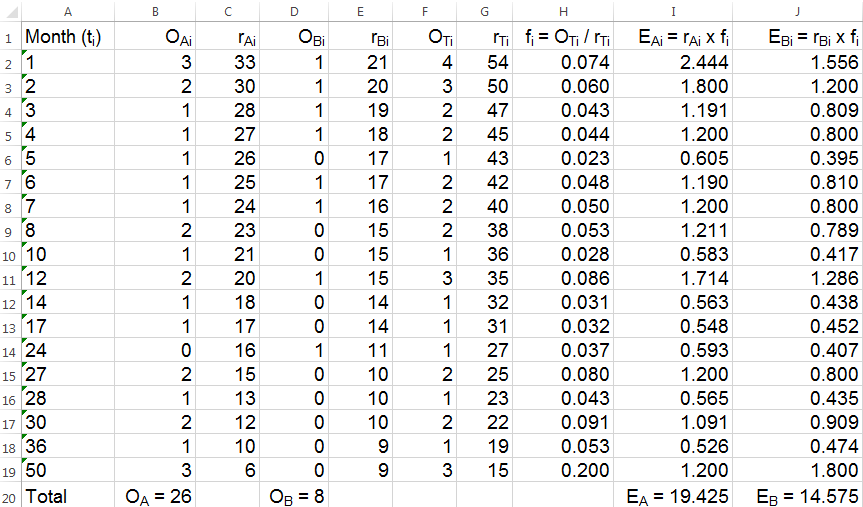
表5中的变量多数都有两个下标：第一个下标代表疗法的分组，A或者B。下标符号为T时表示同一行中A组和B组计数相加；第二个下标i还是时间点序号。变量O代表时段内发生死亡事件的人数，变量r代表时段起点的存活人数，变量f代表时段内两组累计的死亡比例。r与f的乘积就是时段内的预期死亡人数，用E变量来表示，这和卡方拟合优度检验中的E变量是同一个概念。重要的是，发生删失的时间点由于对E变量的计算没有直接贡献而无需列入表5，但是相应的删失病人数需要从下一时段的r值中扣除。

对于熟练的临床生统专家而言，琐碎的计算过程早就被隐藏在简单的几行代码背后而由电脑来完成。但对于生存分析的初学者而言，若能在阅读本文时拿起纸笔对表5中行间与列间的联系进行简单验算，将会有助于彻底掌握对数秩检验的神髓。算出各时段内E变量的数值后，我们将表5中的四列数字累加，就得到了与前文孟德尔豌豆杂交实验结果的卡方拟合优度检验非常相似的四个数值：OA，OB，EA，EB。对数秩统计量最简明的计算方法可以采用下面的卡方公式：

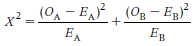
该统计量在零假设前提下也近似遵循自由度为1的卡方分布。把相应的数值代入公式，我们得到的结果是：2.22 + 2.96 = 5.18。运用统计学软件或者查卡方分布的累积概率表，可以算出当统计量为5.18时的对数秩检验概率值：p = 0.023 < 0.05。因此试验数据提供了足够的证据让我们拒绝零假设而采纳备择假设：异体移植组和自体移植组的两条生存曲线有统计显著性差异。有兴趣深究对数秩检验的读者，不妨先验证OA + OB = EA + EB。随后可以研读生存分析的常用教科书 (比如图2来源的那本)，掌握另一种运用方差的对数秩统计量估算法。由此通过笔算或专业软件得到的卡方值为5.48，通常与本文采用的算法结果相似。
 

仅仅确立两种疗法差异的统计显著性 (statistical significance) 还不能让临床医生们完全满意，他们还想知道这个差异的幅度有多大。如果我们对图7中的两条生存曲线“横切”与“纵切”，虽然能提取出反映临床显著性 (clinical significance) 的一些数值，但是它们只是生存曲线“电影”的几个“截屏”。例如本例中自体移植组的中位生存期是17个月，而异体移植组的中位生存期尚未达到 (not yet reached, NYR)，该“截屏”说明异体骨髓移植疗法在临床上有优势，但却不能在整体上说出这个优势有多大。
 

其实我们在基本概念一节中定义的风险比 (HR) 才是衡量临床显著性的更重要指标，它的数值体现了两条曲线的整体差异度。虽然Cox回归分析是临床生统实践中更为常用的估算HR方法，但是对数秩方法也能用一个简单公式来近似估算HR [12]，它与用Cox模型算出的HR在样本数足够大的渐近意义上等价：

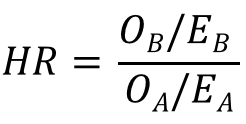
将前文算出的四个数值代入该公式，我们得到的HR数值为0.41，也就是说异体移植组病人的死亡风险比自体移植组病人下降了59%左右，这无疑体现了异体骨髓移植的巨大临床优势。作为比较，用R语言的Cox回归分析算出的HR数值是0.39，与对数秩方法的估算非常接近。HR数值代表的相对死亡风险下降程度虽然更加重要，但也不宜把它看成是衡量临床显著性的唯一指标，对生存曲线的多点横切与纵切可以起到辅助作用，从而为临床医学工作者提供一幅完整的画面。

致谢：在修订本文的2016年初稿过程中，北京天坛医院谷鸿秋博士、美国Karyopharm Therapeutics公司汤诗杰博士、美国斯坦福大学统计系田鲁教授先后提供了有益的建议，笔者在此特别感谢。

参考文献

[1] Weinberg, R.A. (2013) Chapter 15, The Biology of Cancer, 2nd ed. Garland Science, Taylor & Francis Group, LLC.

[2] Hodi, F.S. et al. (2010) New England Journal of Medicine 363: 711-723.[3] Linoff, G.S. & Berry, M.J.A. (2011) Chapter 10, Data Mining Techniques: For Marketing, Sales, and Customer Relationship Management, 3rd ed. Wiley Publishing, Inc.[4] Glantz, S.A. (2012) Chapter 11, Primer of Biostatistics, 7th ed. The McGraw-Hill Companies, Inc.[5] Marks, H.M. (2004) Clinical Trials 1: 131-138.[6] Kaplan, E.L. & Meier, P. (1958) Journal of the American Statistical Association 53: 457-481.[7] Peto, R. & Pike, M.C. (1973) Biometrics 29: 579-584.[8] Baker, M. (2016) Nature 531: 151.[9] Tamarin, R.H. (2001) Chapter 4, Principles of Genetics, 7th ed. The McGraw-Hill Companies, Inc.[10] Dallal, G.E. (2012) The Little Handbook of Statistical Practice  (http://www.jerrydallal.com/LHSP/dof.htm)[11] Vey, D. et al. (1994) Bone Marrow Transplantation 14: 383-388.[12] Machin, D. & Gardner, M.J. (1988) British Medical Journal 296: 1369-1371.