撰文 | 倪忆

传奇数学家张益唐近日公布了他关于朗道-西格尔零点猜想的论文，并在11月5日山东大学的在线讲座中介绍了这一工作。张益唐还将于11月8日在北京大学做线上学术报告。

张益唐这一成果的意义十分重大，如果证明无误的话，将是解析数论领域里程碑式的工作。我们在《千呼万唤始出来，张益唐公布证明朗道-西格尔零点猜想的论文》一文中，试图从外行的角度解读张益唐的工作。山东大学的解析数论专家在《张益唐教授谈朗道-西格尔零点猜想研究的新突破》一文中也进行了专业解读。

在我们前面发表的文章中，对张益唐工作的解读可以总结如下：朗道-西格尔零点猜想是广义黎曼假设的一个重要的特殊情况，但跟黎曼假设没有直接关系。张益唐证明了朗道-西格尔零点猜想的一个变形。这一成果在解析数论中的意义，比张益唐之前在孪生素数猜想上的突破还要重大。

许多读者非常关心的一个问题是，如果张益唐的论文正确的话，他到底有没有证明朗道-西格尔零点猜想？对此，笔者的看法是，这不重要。数论是一门研究整数性质的数学分支。朗道-西格尔零点猜想本身并不是数论问题，而是一个复变函数问题，是对狄利克雷L函数可能的零点的大小的估计。数论学家们之所以会关心这个问题，是为了它在数论中的广泛应用。

在研究一类解析数论问题时，如果狄利克雷L函数的一个零点非常接近1，对于证明就会有很大影响。朗道-西格尔零点猜想的本质就是说L函数的实零点距离1不那么近。具体在量化距离远近的时候，朗道-西格尔采用的标准是

，

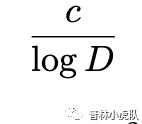猜想和1之间的距离小于这个数的实零点（即西格尔零点）不存在。那么现在张益唐就相当于用另外一种方式来量化这个距离，他宣称和1之间的距离小于

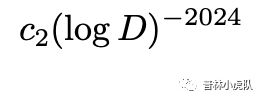
的实零点不存在。这个结论比原来版本的朗道-西格尔零点猜想要弱，但对于数论中的应用已经足够了。即便以后有人能解决原来版本的朗道-西格尔零点猜想，也不会给数论学家带来更多实质上的帮助。

从这个角度来说，认为张益唐解决了朗道-西格尔零点猜想也未尝不可。我们之所以说张益唐证明了朗道-西格尔零点猜想的一个“变形”（variant），就是因为这一说法比说他证明了该猜想的“弱版本”更能准确地反映这一成果的意义。

在张益唐新公布的论文第一章中，他宣布了两个定理，分别是对于L(1,χ)的估计
 

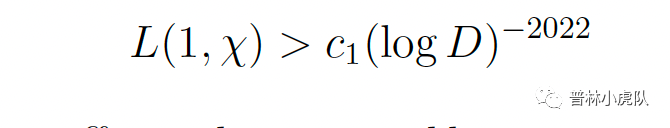
以及对西格尔零点的估计：可能存在的西格尔零点不大于

.

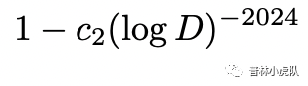其中c1和c2都是跟D无关的，可以计算出来的正实数。

“可以计算出来的”意思就是可以顺着证明过程，一步一步地把这个常数因子具体算出来。有的定理只会告诉你存在这么一个常数，但是你没法根据证明过程算出这个常数到底是多少。对于朗道-西格尔猜想的数论应用来说，知道这个常数的具体数值是非常关键的。

上面的指数-2022和-2024都是可以改进的数字，就像他的孪生素数猜想论文中的七千万一样，只是为了计算方便而选取出来的。当然选取成目前的数字，明显是在致敬今年的年份。

当年在张益唐的孪生素数猜想论文发表后，数论专家们发起了一个Polymath项目，将张益唐文中的七千万最终改进为246. 如果张益唐现在的工作得到证实，可以想象同样会有很多专家来改进他的估计。这里的改进有两方面，一方面是要具体算出两个常数c1和c2的值，另一方面是改进其中的指数，争取把2022和2024缩小。比起孪生素数猜想的情形，这些改进的意义要大得多，因为要想把张益唐的工作应用到数论问题中，肯定是所得到的估计越强越好。

在国外reddit、mathoverflow等网站上，许多网友对张益唐的工作发表了评论。一位网友说：“我确信他为了能在2023年之前把论文写出来而争分夺秒地工作。”下面回复：“哦，张益唐和他有趣的常数。如果这篇文章正确，大家会很兴奋地看到另外一个改进常数的狂热polymath项目。”
 

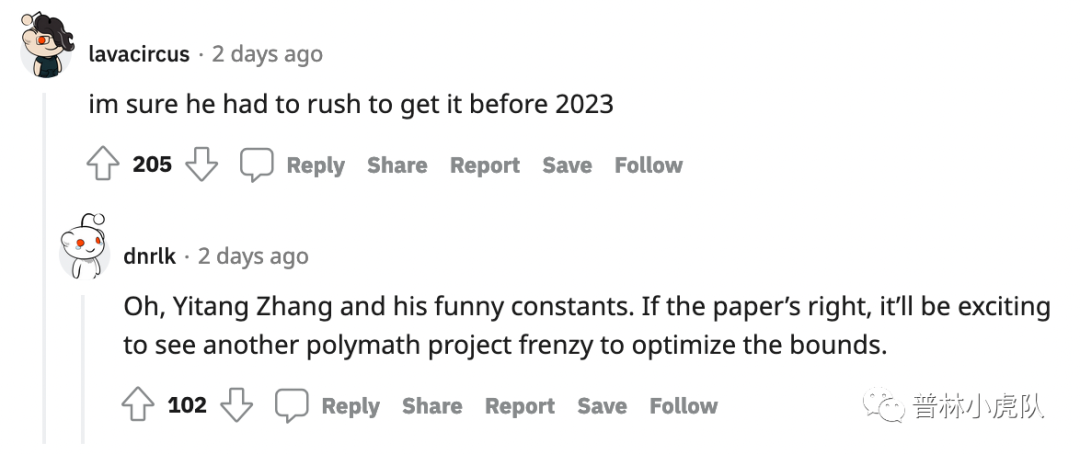
此外还有别的一些犀利吐槽：“如果这篇论文不能在今年底之前发表，我会很不爽。”“如果他工作得更努力，就能在去年写出这篇文章，得到一个更好的指数-2021。”“突发新闻：Polymath项目为了改进张益唐的指数而发明时间机器。”
 

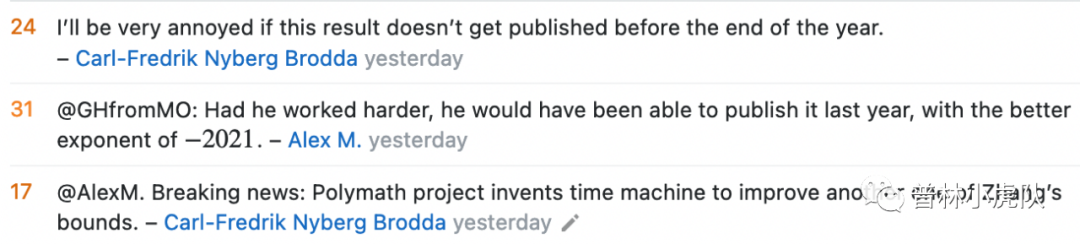
不过，也有一些网友发表了专业性的评论。其中，最引人注目的一个评论是一位叫Stopple的网友发表的。如果读者近期关注张益唐的相关新闻，可能对这个名字不感陌生。此君就是张益唐的同事，解析数论专家Jeffrey Stopple。他曾说：“如果张益唐能够证明朗道-西格尔零点猜想，就相当于一个人被闪电击中两次。”这句话最近被新闻广泛引用，以说明张益唐的工作是多么令人震惊。

Stopple指出，张益唐的成果能够用来研究欧拉和高斯遗留下来的一个关于“方便数”（idoneal number）的问题，把它化为有限次计算。这一问题在文献中并没有公认的名字，我们姑且称之为“方便数猜想”。在张益唐的工作之后，这一猜想或许很快就会成为定理。

那么，这是一个什么样的猜想呢？（以下关于方便数猜想的介绍主要参考了Günther Frei和Ernst Kani的综述文章。）

要介绍“方便数猜想”，需要追溯到17世纪的法国数学家费马。费马考虑过这样一个问题：哪些自然数可以表示成两个平方数的和？例如1、2、4、5等数能表示成平方和：

1=0+1, 2=1+1, 4=0+4, 5=1+4……

而3、6、7等数就不能表示成平方和。费马完全解决了这个问题。对于素数这种特殊情况，费马的结论是，一个奇素数是平方和当且仅当它是4k+1的形式，其中k是一个整数。
 

图卢兹市政厅内的费马雕像

进一步可以问，如果一个数能表示成平方和，那么有多少种方式？例如25可以表示成0+25，也可以表示成9+16；65可以表示成1+64，也可以表示成16+49。这个问题也得到了圆满解决，特别地，4k+1型的素数恰好只有一种方式表示成平方和。

在费马之后一百多年，欧拉进一步研究了这个问题。他证明了，如果一个大于1的奇数m只有一种方式表示成平方和x2+y2，并且在这唯一的一种方式中，x和y互素，那么m就是一个素数。（“x和y互素”即x和y仅有1这一个公约数。这个条件很重要，例如45只有一种平方和表示9+36，但它不是素数。）

这一定理可以用来判断一个4k+1型的数是不是素数，比直接根据定义来判断更便捷。举个例子，如果要判断97是不是素数，我们先写出小于它一半的所有平方数：0, 1, 4, 9, 16, 25, 36. 然后再从97中分别减去这些数，得到：97, 96, 93, 88, 81, 72, 61. 这其中恰好只有一个平方数81，所以97只有唯一一种平方和表示42+92. 我们又能看出4和9互素，所以97是一个素数。

但是4k-1型的数就不能使用这个判别法。为了能够判断这些数是否是素数，欧拉考虑了把自然数表示成x2+2y2或者x2+3y2的形式，并证明了相应结论。例如他证明了一个奇素数能表示成x2+2y2的形式当且仅当它是8k+1或者8k+3的形式。更进一步，如果一个大于1的奇数m只有一种方式表示成x2+2y2，并且在这唯一的一种方式中，x和y互素，那么m就是一个素数。

欧拉画像丨图源：维基百科

受这些结论的启发，欧拉提出了“方便数”（拉丁语numeri idonei，英语idoneal number或者convenient number）这个概念。一个正整数n被称为方便数，如果它满足以下性质：如果一个大于1并且跟n互素的奇数m只有一种方式表示成x2+ny2的形式，并且在这唯一的一种方式中，x和y互素，那么m就是一个素数。

欧拉的工作表明，1、2、3都是方便数。他随后发现了一个简单的方法，可以判断一个给定的正整数是否是方便数。利用这一判别法，他研究了一万以内的所有正整数，发现其中只有65个方便数，罗列如下：

可以观察到，在1848之后就不再出现新的方便数了。于是欧拉在1778年猜测，以上这些就是全部的方便数。这就是我们所说的“方便数猜想”。

1798年，高斯写出了他的名著《算术研究》。在这本书中，高斯系统地研究了整系数二次型，在这一理论体系下赋予了方便数新的含义。这涉及到代数数论里的一些基本概念，限于篇幅，我们就不作说明了。高斯同样猜测1848就是最大的方便数。（欧拉的猜想当时尚未发表。）
 

高斯画像丨图源：维基百科

在高斯之后，很多数学家都研究过方便数。1973年，Peter Weinberger利用日本数学家竜沢周雄在朗道-西格尔零点猜想方面的进展，证明了除去已知的65个方便数以外，最多只有两个方便数。如果有两个的话，其中一个一定是另一个的四倍，所以本质上是同一种情况。（Weinberger后来成为一名计算机科学家，是AWK程序设计语言的作者之一。）

根据Stopple的评论，由张益唐的工作能够证明，存在一个（很大的）自然数N，使得大于N的自然数都不是方便数。这样一来，为了证明方便数猜想，只需要对不超过N的自然数逐一验证便可。至于N究竟是多少，取决于张益唐定理1中的具体估计。在忽略常数因子的前提下，Stopple算出N可以取0.75×1025734. 这当然是一个天文数字，但毕竟还是一个有限的数，并非无穷大。如果能够大幅改进张益唐的估计，或许可以把N缩小到一个适合用计算机加以处理的范围，从而证明方便数猜想。

张益唐本人曾说，在他的突破之后，“一百个猜想都变成定理”。或许这个有244年历史的方便数猜想就是其中之一。当然，所有一切都建立在张益唐论文是正确的基础之上。希望解析数论领域的专家们能够早日完成对张益唐论文的检验，使得一切悬念得到破解。

本文经授权转载自微信公众号“普林小虎队”。