撰文 | 陈关荣
 

百岁长寿的数学家并不多见，大家熟识的两位中国人是108岁的浙江大学朱良璧教授（1913年11月–2021年11月20日）和101岁的复旦大学苏步青教授（1902年9月23日–2003年3月17日）。

朱良璧曾在国际顶尖权威期刊《数学年刊》（Annals of Mathematics）发表过一篇论文，是迄今为止唯一的一位在此刊物上发表过论文的中国女数学家。苏步青是中科院院士，曾任复旦大学校长，主要从事微分几何学和计算几何学方面的研究，是中国微分几何学派的创始人。

在世界范围内不难数出十来个年龄相仿的高龄数学家，而其中最长寿者应数奥地利的拓扑学家利奥波德·维托里斯（Leopold Vietoris，1891年6月4日–2002年4月9日），他辞世时按年头算已经111岁了。他是地球上为数不多的经历过三个世纪、两次世界大战的人。

图1  维托里斯（100岁照片）

01

维托里斯于 1891 年 6 月 4 日出生在奥地利的巴特拉德克斯堡 (Bad Radkersburg) 。 他的父亲雨果·维托里斯（Hugo Vietoris）是铁路工程师，母亲名叫安娜·迪勒（Anna Diller）。雨果曾在维也纳政府中任城市规划主管并参与过多项桥梁建设一是个举足轻重的人物。他非常希望儿子长大后也能成为一名工程师。维托里斯在维也纳读完小学，之后在梅尔克（Melk）的一间天主教本笃会学校就读中学，在那里接受了良好的数学教育。

1911年，他遵循父亲的意愿，进入了维也纳技术大学（Technische Universität Wien），目标是要成为一个工程师。然而，出于兴趣他很快就决定了要当个数学家，并开始努力学习数学和画法几何。在技术大学初期，他也到维也纳大学（Universität Wien）修课。在那里，他被数学家 Hermann Rothe的高等数学课、Emil Müller的几何学课以及 Theodor Schmid 的射影几何学课深深吸引。

维托里斯从Rothe课程里学到了流形的概念，但那时他特别喜欢的是射影几何学。1912年，维托里斯听了著名数学家 Wilhelm Gross 关于拓扑学的演讲。Gross描述了他对Frigyes Riesz公理系统进行扩展的尝试，将数学连续统的概念定义为具有累积点的抽象集合。该新颖思想让维托里斯产生了使用拓扑学方法去建立流形几何的奇想。于是他请教了著名数学家 Gustav Ritter von Escherich 及Wilhelm Wirtinger并和他们一起讨论其可能性。

图2  年轻时的维托里斯

1914年，奥匈帝国对塞尔维亚宣战，第一次世界大战爆发。维托里斯随即自愿参军到了前线。不幸的是，一个月后他就受了重伤。1915年，意大利加入了战争并向奥匈帝国宣战。维托里斯康复后，被派往意大利前线。当时奥地利人控制了山脉，维托里斯平时喜欢爬山于是被派去当军队的登山向导。尽管当时战争条件非常艰苦，维托里斯仍然继续思考他的数学问题，并在1916年取得了一些突破性的进展。他在战场上投稿，发表了平生第一篇论文“第二类四阶空间曲线的一种特殊生成方法”。因此，他得以在春季学期回到维也纳继续修课。1918年初，他的研究取得了更大的进展，并且有机会阅读了数学家Felix Hausdorff在1914年出版的名著“集合论基础”。之后，维托里斯又归队参战。

1918年10月，奥匈帝国战败，维托里斯被意大利人俘虏并囚禁，直到1919年8月才重获自由。在监狱的9个月里，维托里斯的身体得到了很好的治疗。更重要的是，在狱中他完成了博士论文的写作。他被释放返回维也纳后，于1919年12月向维也纳大学提交了以连通集（connected sets）为主要内容、题为“稳定量化”（Stetige Mengen）的论文并于1920年7月获得了数学博士学位。他的两位联合导师是Gustav von Escherich和Wilhelm Wirtinger，就是之前和他一起讨论用拓扑学方法建立流形几何的两位教授。维托里斯的博士论文于1921年发表在《数学和物理月刊》（Monatshefte für Mathematik und Physik）第31卷，被后人认为是他最重要的数学理论贡献之一。

维托里斯在1919年 10 月获得了数学和几何的教师资格。然而，他在高中教书不久就收到了导师Gustav von Escherich 寄来的明信片，祝贺他完成了出色的毕业论文，并为他推荐了格拉茨工业大学（Technische Universität Graz）助理教授的职位。维托里斯接受了教职，在那里成为了 Roland Weitzenböck 教授的助手，后者研究数论和不变量理论。

1922年，维托里斯转回到维也纳大学当助教。在那里，他写了好几篇论文，其中关于二次域的一篇是作为申请永久职位而提交的，得到了著名数学家Hans Hahn的推荐。1927年，他应聘副教授到了因斯布鲁克大学（Universität Innsbruck）。翌年，他又应聘回到了维也纳技术大学，成为数学学院的正教授。1930 年，他折回因斯布鲁克大学出任数学教席正教授，在那里工作至1960年69岁时退休。

1920年代是拓扑学发展的黄金时期。维也纳产生了一批拓扑学家，包括Hans Hahn，Karl Menger，Karl Reidemeister以及后来的Witold Hurewicz 和 Georg Nöbeling。在一个新学科萌发时期，许多新思想会几乎同时间在不同地方独立地出现。维托里斯是一个极其谦虚的人，从不参与优先权的争辩。尽管如此，他被公认为第一个引入“滤子”（filter）概念的人（他称之为“wreaths”）并且是最早定义“紧空间”的人之一（他称之为“lückenlos”），而紧性是滤子序列收敛的条件。他还引入了“正则性”（regularity）概念并首先证明了紧空间是规范（normal）的。

1925年，维托里斯获得洛克菲勒奖金，到荷兰阿姆斯特丹作了三个学期的学术访问。在那里，他加入了由著名数学家L. E. J. Brouwer组织的代数学讨论班，其他参与者还有Pavel S. Aleksandrov，Karl Menger，David van Dantzig，Witold Hurewicz等数学家。受该研讨会代数学思想的影响，维托里斯开始研究代数拓扑学。他回到维也纳之后立即开课讲授同调群和上同调群理论，研究拓扑空间的各种代数不变量。课程里，维托里斯介绍了几个拓扑学猜想，并提供了一些可能的证明思路。一位前来听课的同事瓦尔特·迈尔（Walther Mayer）根据他的建议证明了其中一个猜想，维托里斯随即对证明做了最后的完善，最后两人于1930年建立了代数拓扑学里著名的迈尔–维托里斯正合列（Mayer-Vietoris sequence）理论，把拓扑空间上同调群转化到拓扑子空间中并为这些群的计算提供了一个重要方法。

说起来这位迈尔也是个有故事的人物。他和维托里斯一样，是一战退伍军人。但当年作为犹太人他很难在大学里找到教职，只好经营一间小咖啡店借以谋生。1926年，他得到爱因斯坦的推荐被维也纳大学聘为数学讲师，从而有机会旁听了维托里斯的拓扑学课程。1930年，迈尔出版了《黎曼几何》一书。后来，迈尔成为爱因斯坦在柏林和普林斯顿的助手和合作者，得到一个“爱因斯坦的计算器”（Einstein’s calculator）绰号。

1933年，爱因斯坦在筹划迁居美国时，需要在普林斯顿高等研究院和加州理工学院之间作出选择。当时普林斯顿答应同时给迈尔提供一个永久职位，而加州理工学院的经费则不足以雇请他，于是爱因斯坦选择了普林斯顿。爱因斯坦在给加州理工学院院长的答谢信中说，迈尔对他来说是如此重要以至他必须放弃所有别的考虑。迈尔跟随爱因斯坦加入了普林斯顿高研院后工作到1948年去世。不过，迈尔在后期回到了他自己喜爱的纯数学研究，没有在统一场论的研究中继续充当爱因斯坦的“计算器”。

1938年3月，德国开始吞并奥地利，随后在9月份入侵波兰。于是奥地利对德国宣战，全国陷入战争状态。在这第二次世界大战中，维托里斯再次自愿参军。但这时他已经48岁了。他被送往波兰战场，在那里他又一次受伤。不过，他依然大难不死，继续在军队服役到1941年。难能可贵的是，即使在战争期间，他仍然不时有文章发表。之后，他退伍并回到因斯布鲁克大学重操旧业。这时他不再关注代数拓扑学，转向了概率统计和实分析方面的研究。

维托里斯一生发表了约 80 篇数学论文，其中只有一篇有共同作者。此外，他约半数论文是在60岁之后发表的，其中不乏战时积压下来的手稿。他奠定了一般拓扑学的基础，参与了代数拓扑学的创建。在这个领域里，好几个数学概念和定理以他的名字命名，诸如维托里斯拓扑（Vietoris topology）、维托里斯同调（Vietoris homology），迈尔–维托里斯正合列（Mayer–Vietoris sequence）、维托里斯–里普斯复形（Vietoris–Rips complex）以及维托里斯–贝格映射定理（Vietoris-Begle mapping theorem）。他103 岁时发表了最后一篇论文，是“论某些三角级数和的符号”系列文章的第三篇。为此，维托里斯也被学界称为是“数学的玛土撒拉”。玛土撒拉（Methuselah）是《希伯來圣经》记載中亚当的第七代孙，是世界上最长寿的人，据说他活了969年。

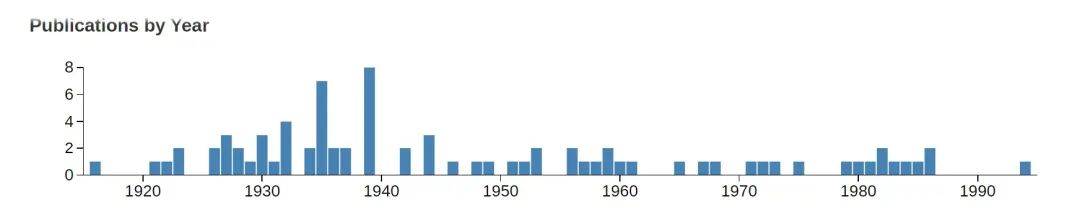
图3  维托里斯发表论文的时间分布

顺便提及，近年来高阶复杂网络和拓扑数据分析的发展开始用到了同调和持续同调等理论和方法。维托里斯对同调论有诸多贡献，迈尔–维托里斯正合列只是其中最著名的一项。他的另外一个重要贡献，维托里斯–里普斯复形，在被数学界遗忘几十年之后又重新获得了极大关注。当年维托里斯等人建立的同调论是单纯同调论，研究单纯复形即由点、线、面、体等最基本的单纯形按一定规则组成的复杂网络图形。从单纯复形出发，可以引入单纯同调群。维托里斯在 1927 年定义的“维托里斯同调”试图把单纯复形扩充到更广泛的空间。维托里斯同调是对于度量空间来构造的，而拓扑结构并不依赖于度量。因此，以度量来构造的“维托里斯–里普斯复形”有好处也有缺点，主要优点是使用度量便于计算。

维托里斯是一位思想纯粹的学者。他在1947年写给 L. E. J. Brouwer的一封信中说道：“作为院长，我被行政事务压得喘不过气来，以至我经常不得不去讲一些准备并不充分的讲座，更没有时间进行科学研究。幸运的是，这个学期很快就要结束了，我希望回去当一名科学家，而不是一个官僚。”
 

图4  维托里斯作学术演讲

维托里斯因其毕生的数学贡献多次受到表彰，主要荣誉包括：1935年，当选为奥地利科学院通讯院士，1960年成为院士；1965年，当选为奥地利数学会会士；1984年，获维也纳技术大学荣誉博士学位；1884年获因斯布鲁克大学荣誉博士学位；1973年，获奥地利科学与艺术学院荣誉十字勋章；1981年，获奥地利共和国服务金奖和 奥地利数学会金质奖章；1982年，获因斯布鲁克市功绩勋章；

1992年，当选为德国数学会会士。

02

维托里斯后半生定居在因斯布鲁克的原因之一是那地方临近阿尔卑斯山。他太喜欢爬山和滑雪了。在那里，他加入了当地由冰川学家组织的登山体校。在数不清多少次的科学探索高山远足中，他总是扮演一个“冰川仆人”（Gletscherknecht）的角色，携带重型仪器进行地质测量和设置科学实验。

他对岩石冰川特别感兴趣，还发表过关于Hochebenkar山区冰石块流和滑雪板弹性物理学的文章，以及“为登山者服务的几何学”的指引。他甚至拥有使用航空照片来绘制地图的专利号（1924 年，100832），描述了一种对航空照片作差分校正以生成正射影像的方法。为此，有人还把他称为“正射影像之父”。他长期在冰山上滑雪，直到93岁时因身体不适在医生强迫性建议下才停止下来。
 

图5  维托里斯和妻子玛丽娅

在个人生活方面，除了登山之外维托里斯喜欢音乐并有虔诚的宗教信仰。在家庭生活方面，维托里斯于1927年和克拉拉·冯·赖兴费尔斯（Klara von Reichenfels，1904-1935）结婚，两人有6个女儿。克拉拉在1935年最后一个孩子出生时去世。次年，维托里斯娶了她的姐姐、当年失婚独处的玛丽娅（Maria von Reichenfels，1901-2002）。2002 年 4 月 9 日，在时满100岁的妻子玛丽娅去世几周之后，维托里斯也在家中平静辞世，享年111岁。

图6  维托里斯传记文集

本文经授权转载自微信公众号“华院计算”。