阅读:0
听报道
两个音色不同的声音,它们的波形是不同的。我们可以把很多正弦波加起来,构成一个复杂的波形。反过来,也可以把复杂的波形,拆开成一个个正弦波。后面这个过程即是数学中的傅立叶变换。
撰文 | 吴进远(美国费米国家加速器实验室)
晚自习之后,我和珍旭班长离开图书馆,一起走在校园里。见我不做声,珍旭班长问:“你前一阵写了不少音乐的文章吧?”
“是的。可是读者们说,讲音乐不能不把傅立叶变换讲清楚。”
“对呀。”
“我其实是写了傅立叶变换的,但读者们认为我写得太晦涩,专有术语太多。”我说:“可是傅立叶变换是大学的课程,没法讲得简单呀。”
“要想把傅立叶变换讲透彻的确需要大学知识。”珍旭班长说:“但你可以先用一些简单实际的例子,做个初步的说明呀。”
见我一时说不出话,珍旭班长示意我在路边长椅坐下,在手机上划了一阵:“给你看看我小时候,爷爷给我讲睡前故事,是怎么讲傅立叶变换的吧。”说着在我身旁坐下。
我顿时觉得心跳加速,脑子里有一段时间一片空白。隐约记得珍旭班长介绍说,这些睡前故事的视频本来是用老式8毫米录像带录下来的,几个月前爷爷奶奶刚把它们转换成数字的视频文件。
1 音色与波形
珍旭班长点开一个视频,屏幕上出现一个毛绒动物熊猫。她介绍说,这是我们家庭成员中最小的一位,叫熊猫晶晶。
“我是熊猫,”小珍旭粗着嗓子扮演熊猫晶晶。
“我吃竹子,”视频中熊猫晶晶仰头摇晃,好像非常骄傲,“我要唱《五指歌》。”
小珍旭稚嫩的童音和爷爷浑厚的男中音一齐唱响:
“一二三四五,上山打老虎。(老虎!老虎!老虎!老虎!——熊猫晶晶惊恐喊道。)”
“老虎打不着(老虎!老虎!老虎!老虎!),看见小松鼠。”
“松鼠有几个,让我数一数。数来又数去,一二三四五。”
见我一头雾水懵在那里,珍旭班长解释道:“熊猫的天敌是各种食肉猛兽,因此熊猫晶晶听到老虎会害怕。”
视频继续,小珍旭问道:“爷爷,我们唱一样的《五指歌》,为什么我们的声音不同呀?”
“这倒是一个好问题。”爷爷说:“不过,你首先要解释清楚,你说的声音不同是什么意思。”
小珍旭从床头柜抽屉里拿出她的儿童口琴,吹了一个音:“咪——”
“咪——”她自己按照这个音高唱出这个音符,然后说:“爷爷唱。”
“咪——”
“熊猫晶晶,”小珍旭捧起毛绒熊猫:“我和爷爷唱的音符一样吗?”
“一样一样。”
“可以听出两个人的声音不同吗?”
“可以可以。”
“哈哈哈,”爷爷笑道:“晶晶说得对,我们两人唱的音符是一样的。都是C调中的咪,也就是E,频率为 659.3 赫兹。”
“既然频率一样,为什么我们的声音仍然可以听出差别呢?”
“这是因为我们的音色不同。”
“什么叫音色?”
“音色和声音的波形有关,”爷爷解释道:“两个音色不同的声音,它们的波形是不同的。”
“什么是波形?”
“我们听到的声音是一种波动,它是振动的物体推动周围空气产生的。振动的物体让周围的空气一会儿压缩,一会儿舒张,使得空气的压强出现微小的强弱变化,于是这种压强的强弱变化就会传播开来,变成声波。”
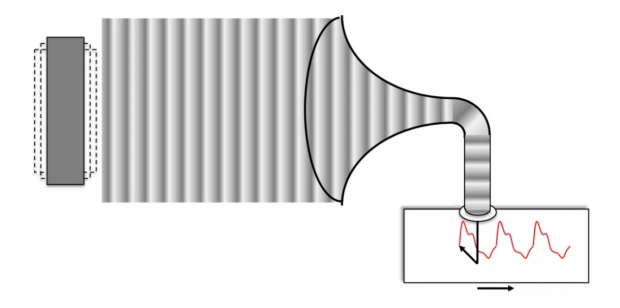
“当声波来到我们的耳朵或者话筒时,耳朵里的鼓膜或者话筒里的膜片就被空气有时推,有时拉。如果把这种推拉运动放大,带动一根针,让它在一张匀速运动的纸上刻画,就可以画出一个波浪一样的图形。刚才我们两人唱的音符是E,频率为 659 赫兹,也就是说,这种推拉运动每秒钟重复 659 个周期。但我们可以听出两个人的音色不同,画出的波形也不同。除了人的声音,不同的乐器也有不同的音色。”
“那么,”小珍旭问:“我的口琴声音波形是什么样的呢?”
爷爷点开电脑上一个软件,小珍旭吹响她的口琴,她吹的是音符E,电脑记录下一个波形。(其实,现在我们在手机的应用商店里,也可以找到显示声音波形的软件。)

“我们再看看别的乐器波形是什么样的。”爷爷拿来一把小提琴,拉响一个音符,也是E。电脑记录下另一个波形。

“呀,口琴和小提琴声音的波形真的很不一样。”小珍旭说:“可是,这些波形里,有那么多上上下下,看着好复杂呀。”
“确实很复杂。”爷爷在电脑上打开另一个软件,说:“不过,复杂毛糙的波形可以看成是一些简单光滑的波形叠加起来的,你看。”
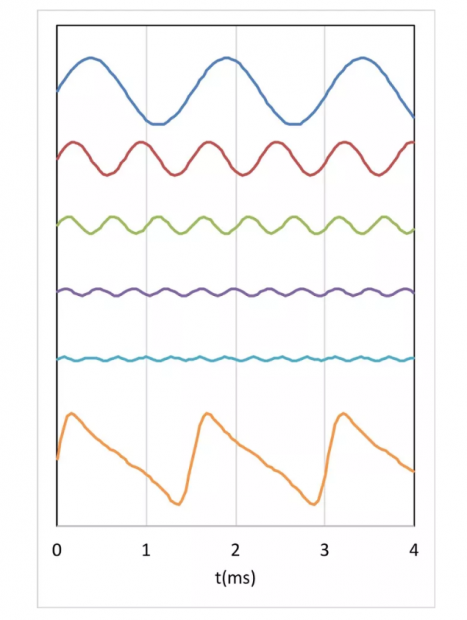
“这里有好几个波形,看着很光滑。”小珍旭说:“最上面那个波动得最慢,往下一个比一个快。”
“对的,这些波形叫正弦波,横坐标是时间,单位是毫秒。最上面那个正弦波的频率是659赫兹,第二到第五个波形,它们的频率分别是659赫兹的2、3、4、5倍。这些整数倍频的正弦波,在音乐上叫做泛音。”
“我会算。”小珍旭抢着说:“659赫兹的2倍是1318赫兹,3倍是1977,4倍是2636,5倍是?5倍是3295。”
“不错,算得挺快。”爷爷表扬道,然后接着解释:“这样一些正弦波,按照一定的比例叠加起来,就可以得到最下面那个波形。”
“什么叫叠加?”
“你在每一个时间点上画一条竖线,每一个波形在这个时刻都有一个高度,把这些高度像叠罗汉那样加起来,就叫叠加。”
“真有趣,本来几个光滑的正弦波,叠加起来就变得像锯齿一样了。”
“你再看看这个。”爷爷在电脑上改了几个数。
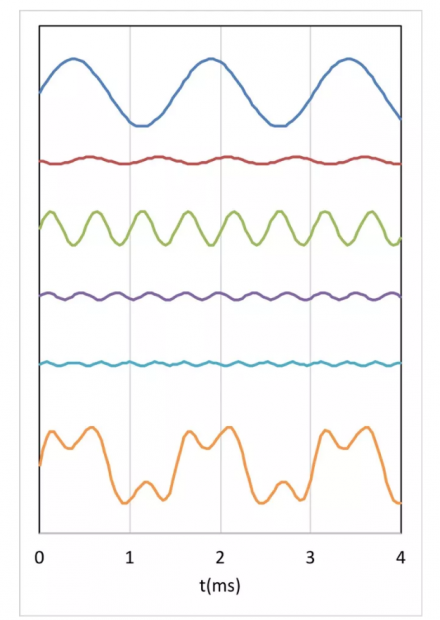
“咦,叠加出来的波形变得像方方的馒头了。您在电脑上改了什么呀?”
“这些正弦波还是原来的频率,我只不过改了一下这些正弦波叠加时振幅的比例。你比较一下两个图,就可以看出有的频率成分变大了,而有的变小了。”
“这就是说,”小珍旭若有所思,“不同频率的正弦波,叠加时的比例不同,形成的波形也不同。也就是说,一个乐器的音色,是这些频率成分,或者说泛音的比例决定的?”
“不错,总结得很好。把一个复杂的波形,分解成为许多正弦波的过程,叫做傅立叶变换。”
“噢,我明白了。我们可以把很多正弦波加起来,构成一个复杂的波形。反过来,也可以把复杂的波形,拆开成一个个正弦波。”小珍旭的确天资聪颖。“可是,怎么才能拆开呢?”
“明天还要上学,且听下回分解。”爷爷逗她。
小珍旭显然不想睡,于是像演木偶戏那样举起熊猫晶晶:“爷爷,晶晶不懂。请爷爷,用熊猫和竹子作为例子,给晶晶再讲一讲。”
“一只熊猫,拿着一根竹子,一边走,一边在地上画。如果只有它的腿在左右摇晃,那么在地上画出来的波形就比较简单光滑。可是今天熊猫吃饱了嫩竹笋很高兴,身子也在摇晃,走一步摇晃两次。胳膊也摇晃,走一步摇晃三次。手也摇晃,走一步摇晃四次。这样一来,就会在地上画出一个很复杂的波形。晶晶懂了吗?”
“懂了懂了。”
“好了。现在熊猫晶晶回到床头柜上,小珍旭盖好被子,睡觉。”
2 通过共振理解傅立叶分析
第二天晚自习之后,我和珍旭班长在校园长椅上接着看视频。我想看看爷爷怎样讲解把复杂波形分拆为正弦波,当然,我更享受和女神在一起的美好时光。
“我是熊猫,我吃竹子,我要唱《五指歌》。”
“一二三四五,上山打老虎。(老虎!老虎!老虎!老虎!)……”
好嘛,她们家睡前故事还挺讲究程式化的。后来珍旭班长告诉我,她的节奏感还有和声知识,都是通过唱《五指歌》学的。
视频里,爷爷开始讲故事:“从前有座山,山里有个庙,庙里有个老和尚。他房间里有个磬,经常自己发出声音,有时在白天,有时在黑夜。老和尚以为有妖怪,吓得生了病。”
“这是个唐朝的故事,我知道,叫《曹绍夔 (kuí) 捉妖》。”小珍旭抢着说:“后来,老和尚的朋友,洛阳一个管音乐的官叫曹绍夔的来看望他。正好赶上庙里敲钟,磬也跟着响了起来。于是曹绍夔大笑,让和尚第二天准备好酒好菜,他来捉妖。第二天,曹绍夔来了,酒足饭饱之后,拿出一把锉刀,在磬上锉了几下。以后磬就再也不响了。”
“这是为什么呢?”
“这是因为钟声的频率和磬的共振频率一样,敲钟的时候,声波引起磬共振。曹绍夔在磬上锉了几下,把它的共振频率改变了,就不会再共振了。”
“讲得对。”爷爷说:“现在我们把这个故事拓展一下,设想老和尚房间里放了好多个磬,它们的共振频率从低到高各不相同。如果你去了,随便唱出一个音,情况会怎么样呢?”
“我觉得,那么多的磬,不管我唱什么音,总会有一个的共振频率和我唱出声音的频率接近,所以应该会引起共振。”
“只会引起一个磬共振吗?”
“这?”小珍旭苦苦思索。
“我们昨天讲了,当我们唱一个音符时,比如唱E,里面除了 659 赫兹的频率成分,还有哪些?”
“还有 659 赫兹的2、3、4、5 等倍频的正弦波,或者叫泛音。它们的频率是 1318、1977、2636、3295 赫兹。”小珍旭豁然开朗:“也就是说,我唱出一个音,会引起很多个磬一起共振,只要它们的共振频率与这些泛音频率相近。”
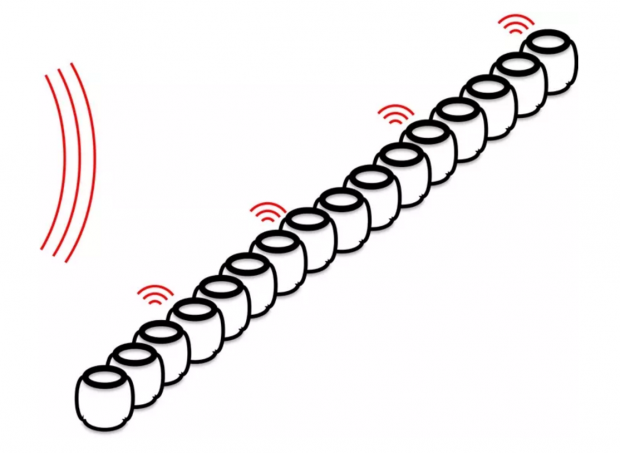
“这样一来,我们就知道你唱的声音里有哪些频率成分。而且,根据这些共振的相对振幅,我们就可以知道这些泛音之间振幅的比例。这其实就可以看成是傅立叶分析。”
“傅立叶分析?”
“傅立叶是个法国的数学家,和肖邦差不多同时代,比肖邦年龄大一些。”
“可是,”小珍旭问:“要作傅立叶分析,到哪里去找那么多磬呢?”
“不一定非得用磬,用弦也可以呀。钢琴里不是有很多弦吗?”爷爷说:“我们可以到客厅用钢琴做个实验。”
小珍旭噌的一下,穿着睡衣睡裤从被窝里跳了出来。
“披上衣服。”拍摄录像的奶奶在画面外喊道。
爷爷和小珍旭趴在地板上,轻轻地取下钢琴底部的盖板,按下钢琴的右踏板,使得钢琴的所有琴弦可以自由振动。
“咦,钢琴里有声音,好像我们说话的回声一样。”
“你试试对着钢琴喊一声。”
“啊——”小珍旭喊道。
钢琴跟着发出微弱的声音,听起来和小珍旭的声音非常像。
爷孙两个对着钢琴喊话、唱歌、学牛叫、学狼叫,钢琴都会随之发出相应的声音。
哈哈,钢琴华丽变身为傅立叶分析仪,不知道大钢琴家肖邦当年有没有试过。他经常在巴黎的沙龙里给那些绅士贵妇们演奏,听众中很可能有过傅立叶。如果他在演奏时,顺便表演一下这个“魔术”,也许会减少一点演奏的辛苦吧。我不知怎么,脑回路里搭出这么一个念头。
其实这个实验我也做过,我在手机上找到一个图给珍旭班长看:“用这个图,可以把整个实验过程看得更清楚。”
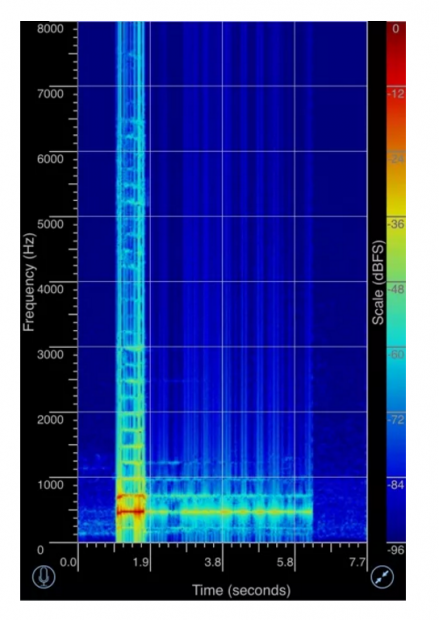
这个图是使用手机的APP Spectrum View 来记录的谱图。横坐标为时间,纵坐标为频率,每个频率成分的强度用颜色显示。
在图中,开始有0.8秒左右我们对钢琴喊出一个持续稳定的声音,显然,这段时间内声音的强度比较大。这个声音的基频大约是250 Hz左右,不过它的基频成分强度不是很大,而是以2倍频与3倍频为主。此外还存在很多高倍频的成分。
喊声停止后,我们可以看出钢琴上对应于1到5倍频的琴弦被显著地激励起来,并持续振荡。
实际上,在喊声停止后约1秒左右的时间内,钢琴发出的声音与原来的人声非常像,而过了一会,虽然钢琴还有声音,但已经与原来的声音不像了。这是由于开始时,钢琴能够按照原来声音的比例发出4倍与5倍频成分。随着时间推移,这些高频成分衰减很快,等到只剩下低频成分时,声音的相似度就会变差。从图中我们可以看出4倍与5倍频成分衰减得相当快。
3 相位与音色之谜
“你们在看什么呐?”泉余室友又一次毫无征兆地出现了。
“我们在学习儿童睡前故事版的傅立叶变换。”
“正好,我有个青年失眠烧脑版的问题。”泉余室友说着,从口袋里掏出一叠皱皱巴巴的纸:“你们帮我看看。”
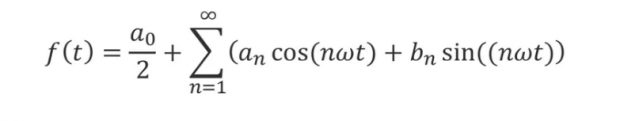
“一个周期函数f(t)可以展开成为傅立叶级数,写出来是这个样子。你们注意到了吧,每个频率成分包含有两个系数。”
“是啊,包含a和b,它们分别是余弦函数和正弦函数的系数。通过这两个系数,我们可以算出每个频率分量的振幅和相位。”
“可是,我们讨论频谱时,很多时候比较关注振幅,很少注意相位。”泉余室友说:“手机上的傅立叶分析软件也经常是只显示强度分布,不显示相位关系。这是为什么呢?”
“我觉得,原因之一是在很多实际应用中,频率分量的强度比较重要,而相位相对不很重要。比如我们的耳朵辨别音色时,只能感知各个频率成分之间的相对强度比例,而不能感知它们之间的相位关系。” 珍旭班长边说边掀开笔记本电脑:“你们看。”
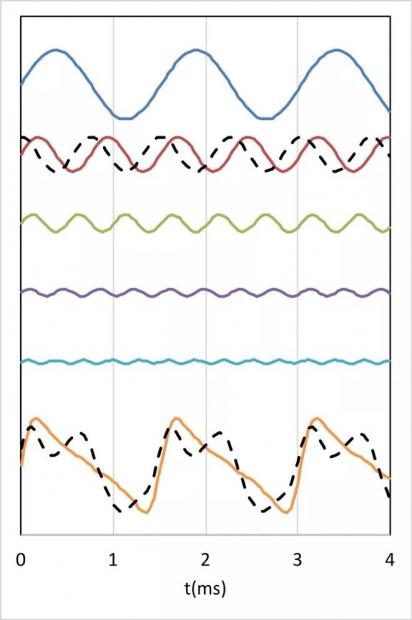
“我们用基频和几个整数倍频的正弦函数可以近似构成一个锯齿波。可是如果我们让二次倍频的振幅不变,只改变一下相位,把它从正弦函数变成余弦函数,最后组合出的波形就会改变。”
“对呀,倍频成分的相位变了,波形自然也会改变。”泉余室友说:“那么,我们的耳朵能听出来吗?”
“在这种情况下,”珍旭班长说:“各个频率成分的相对强度没有变,因此我们的耳朵听不出来,感觉还是原来的音色。”
“什么?”我大惑不解:“你说声音的波形变了,音色可以不变?视频里,爷爷怎么说的?”
“爷爷说的是:两个音色不同的声音,它们的波形是不同的。”珍旭班长解释:“但反过来却不一定。”
“珍旭同学,”泉余室友一本正经地开玩笑说:“我很尊重您,但我更尊重科学。我还是无法不经过思考,盲目相信您的说法。”
“要不要做个实验?”珍旭班长说。
“好啊。”我赞成:“一言不合做实验,这才是我们物理系学生的风格。”
“我负责生成声音信号。”珍旭班长拿起手机:“你们也都拿出手机,一个负责观察频谱,一个负责观察波形。”
珍旭班长点开手机软件,在上面输入了500、1000、1500、2000 和 2500 赫兹这几个频率值。
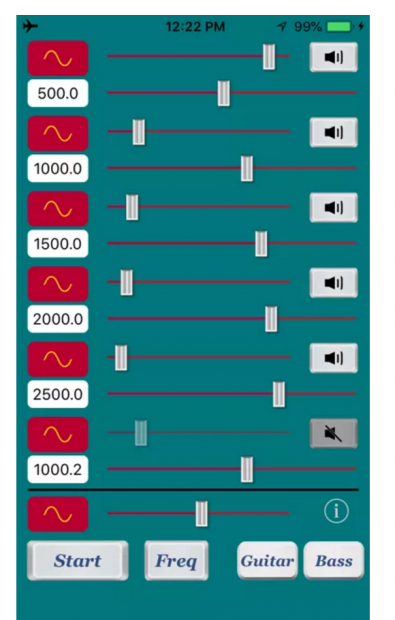
又点了一下屏幕,这样一个混合的声音播放了出来,听着好像是鹄鸬鸟的叫声。我们把手机凑到一起,我在频谱上看到几个尖峰,泉余室友手机上显示了一个奇形怪状的波形。
“现在我把 1000 赫兹改成 1000.2 赫兹。”珍旭班长说:“这样一来,等价于让1000 赫兹频率成分的相位缓慢变化。”
现在这个混合的声音听上去和刚才几乎没有不同,还是鹄鸬鸟的叫声,尽管其中一个频率成分的相对相位持续缓慢地变化着。从频谱上看,几个尖峰也没有变化。可是,泉余室友手机上的波形,却像小虫子一样不停地蠕动着。(见实验视频)
“好了,现在敲黑板。”珍旭班长有些得意:“期末考试部分选择题如下。”
(1)音色不同则波形不同。答案:对
(2)波形不同则音色不同。答案:很多时候如此,但不一定。
“嗯,我现在认同这个理论了。”泉余室友说,可是仍然故意嘴硬:“但并不是因为听了您的讲解,而是因为看见了实验结果。”
“这有什么不同吗?”珍旭班长酣畅淋漓地发挥她的伶牙俐齿:“我不是也要按照前人实验的结果来讲吗?不过你这种科学态度应该表扬。对于科学问题,应该不迷信盲从他人,包括不迷信盲从班长、朋友乃至学术权威,坚持通过自己的思考理解科学结论。在这个问题上,我俩尊你为师。”
“你俩?”泉余室友掩口而笑。
版权说明:欢迎个人转发,任何形式的媒体或机构未经授权,不得转载和摘编。转载授权请在「返朴」微信公众号内联系后台。
话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 