本文为《物理学咬文嚼字》027，原名为熵非商-the Myth of Entropy。熵是温度关于能量的共轭量，脱离温度理解熵，难免不着边际。此次趁同“什么是温度？” 一起发表之机，又增添了两条补缀。

 

撰文 ∣ 曹则贤（中科院物理研究所研究员）

 

道可道，非常道；名可名，非常名。

 

——老子《道德经》

 

糟粕所传非粹美，丹青难写是精神。

 

——王安石《读史》

 

摘要： 就不易理解和容易误解这一点来说，entropy是非常特殊的一个物理量。Entropy的本意是一个同能量转换相关的热力学广延量，中文的熵，或热温商，是对克劳修斯公式形式上的直译。Entropy是一个具有深远意义的基础概念，量子力学以及后来的通讯理论都得益于熵概念之上的深入研究。

 

热力学（thermodynamics）是大学物理教育中不可或缺的一门基础课，我印象中这是一门教的人和学的人都倍感困惑的课程。我在德国乡间一所大学读书的时候，在机械系一间实验室的窗框上读到过这样的一段话，原文记不住了，大意是“热力学是这样的一门课：你学第一遍的时候觉得它挺难，糊里糊涂理不清个头绪，于是你决定学第二遍。第二遍你觉得好像明白了点什么，这激励你去学第三遍；第三遍你发现好像又糊涂了，于是你只好学第四遍。等到第四遍，well，你已经习惯了你弄不懂热力学这个事实了。” 我一向认为笑话也是来自生活的，所以看到这段话我会心一笑。别人怎么回事我不知道，反正热力学于我来说大约就是这么样的困难。况且，人家说这话的时候读的是自己的先辈克劳修斯（Rudolf Clausius）、 玻尔兹曼（Ludwig Boltzmann）、普朗克 (Max Planck) 等热力学奠基人用自己的母语撰写的书，而我们读的却是物理教师用中文转述或编或凑的课本。你会发现中文热力学教科书热衷于在那儿来回捣鼓麦克斯韦（James Clerk Maxwell）关系式，但到底那些微分表示在什么情况下才是真正有意义的物理量，一个麦克斯韦关系表示的是什么物质体系的哪些物理量在什么条件下的关联，作者们似乎懒得理会。甚至各种自由能啊热力学势啊是针对什么样的体系提出的，是否都是基于同样地也需要证明和辩护的热力学第二定律，也是一笔糊涂账。至于一百多年前一帮子英国人、法国人、德国人是如何艰难地凭经验构造热力学的，热力学如何导致量子力学关键概念的产生和薛定谔（Ervin Schrödinger）方程的推导，热力学又是如何发展成了统计力学的，这些问题更是鲜有提及。而热力学就一直这样被恐惧着、误解着，它在整个物理学体系中的重要性也未能得到充分的强调。

 

如果要给热力学指定唯一的关键词的话，笔者以为最恰当的是entropy （汉译熵）。熵是一个体系之作为热力学体系所特有的广延量，是热力学的灵魂。可以说，如果一个体系的物理学描述不出现熵这个物理量，它就不是一个热力学的问题。熵是和温度相联系的，实际上温度是熵关于能量的共轭，但温度并不总是可以定义的（1）。一般的印象是，所谓研究物质的热力学性质就是研究物质的某些特性随温度的变化，这里的一个未明言的假设（tacit assumption）是，我们关切的是一个同热库取得热平衡的体系，赫尔姆霍兹（Hermann von Helmholtz）自由能是描述体系的合适的热力学势（2）。这样做的好处是，温度是一个可操控的外部控制参数。温度一般会被混同于冷热的感觉，温度的概念比熵出现得早，但并不是说温度就比熵是更基本的。人们之所以把热力学性质看成是物理性质对温度的依赖而不是表达成同熵的关联，笔者揣测是因为人们还不习惯于面对熵这样的emergent的概念 （见下文）。熵是一个非常独特的概念，就不易理解和容易误解这两点来说，在整个物理学领域，熵都是鲜有其匹的一个词。

 

 

Entropy 一词传入中国，据文献说是在1923年5月25日。I. R.普朗克 （原文如此）来南京讲学，在南京东南大学作《热力学第二定律及熵之观念》等报告，胡刚复教授为普朗克做翻译，首次将entropy译为熵 [2]。其根据是公式 ds=dQ/T，因为是热力学概念，从火；此表达式又是个除式，为商，故名为熵！文献[3]中有 “濮朗克教授（是否Max Planck待考）……讲 ‘热学之第二原理及热温商（entropy) 之意义’”的说法， 但也未敢断言。笔者未能找到胡刚复教授翻译entropy的确切中文文献记载。此外，笔者印象中德国物理学家名普朗克的对热力学有贡献的科学家就是Max Planck，虽然普朗克被认为是量子概念的创始人，但普朗克常数却是研究热力学的结果。笔者翻阅德国物理学会纪念普朗克诞辰150周年文集[4]和普朗克传记[5]，也未见提起1923年曾访问中国一事。Entropy如何转变成了中文的“熵”， 这一点还盼国内科学史家详加考证。

 

中文熵，或曰热温商，确实易让人联想到除式 ds=dQ/T 而非能量转换的内在问题。此公式是计算工具，却不是entropy 的定义。若由熵，或热温商，来理解entropy，难免误入歧途。其根据积分公式而来的汉译有其历史的合理性，但从根本上来说却是错误的，似乎熵的定义或计算依赖温度的存在。熵是比温度更基本的物理量，对温度无从定义的体系，熵一样是可定义、可计算的。虽然历史上是由热力学第二定律导致了熵概念的引入，但热力学的叙述却可以从一开始就引入熵[6]。历史的发展方向常常和自洽理论的结构不一致，这一点应该不难理解。

 

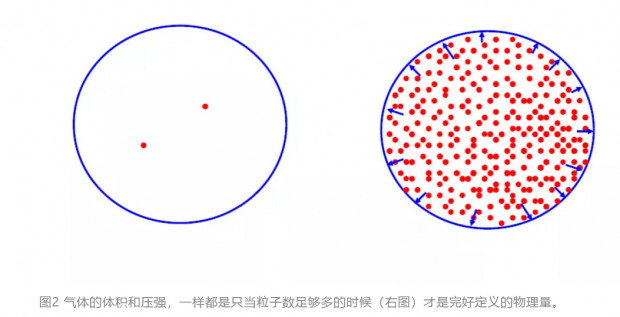
关于熵的性质，应注意到首先它是一个广延量（extensive quantity），应有可加性（additivity)：考察一个具有N1+N2粒子的热力学体系，设想用一个虚拟的隔板（a virtual partition）将体系分割成粒子数分别为N1，N2的两部分，则熵的定义或算法必须满足 S(N1+N2)=S(N1)+S(N2) 。热力学的第一件要务是写出体系的内能 U=U(S, V, N, P, M, ……)，其中熵S、体积V和粒子数N对应的强度量分别是温度T、压强p和化学势μ，是体系的内在性质；而电极矩P和磁矩M对应的分别是外加电场和磁场。理解熵的第二个要点是它是一个emergent 物理量。Emergent本意是冒出来的、突然出现的；emergent物理量是指粒子数增多到某个临界值以上才出现的物理性质，同动量、能量这种对单个粒子也能很好定义的物理量相映衬。实际上，体积、压强也是emergent 物理量，熵并不比体积或压力是emergent更难理解。对于少粒子体系来说，粒子在容积为V的约束空间中游荡，我们很少会把一个大的真空室当作是几个分子气体体系的体积。只当分子数足够多的时候在整个约束空间的每个小区域内的分子密度，或该空间区域被粒子访问的频率，都是抗涨落的（即涨落不对宏观性质产生可感知的影响），我们才把约束空间当作气体体系的体积。同样，对于几个粒子组成的体系，约束的表面会不规则地受到来自粒子的碰撞，但还没有压力的概念。只当分子数足够多的时候在整个约束面上的任意小邻域内单位时间得到碰撞的动量传输是抗涨落的，我们才把约束空间受到的碰撞笼统地用气体体系的压力来表征（图2）。热力学不习惯从一开始就用S作为与V，N等同身份的基础变量来书写，可能是人们还不习惯于处理熵这样的比体积更不直观的emergent物理量。但近几年来emergent phenomenon（3） (呈展现象) 的研究得到广泛的重视[7]，连引力也可从呈展现象的角度看待[8]，相信从一开始就用S,V, N展开热力学讨论的书籍会很快面世。这样的热力学，如同有人对经典力学做过的那样，是用一张PPT就能说清楚了的。

 

 

热力学很大程度上给人以经验（empirical）科学的印象，时至今日许多教科书都直白地表露这一点。为了给热力学奠立坚实的理性的基础，其中至关重要的一点是如何理解不可逆性或热力学第二定律，玻尔兹曼（Ludwig Boltzmann）为此进行了艰苦卓绝的探索[9]。篇幅所限，不能详述玻尔兹曼的工作，此处仅指出玻尔兹曼基于原子假设，把事件的不可能性（impossibility）表述成了相应体系状态的极小概率 (improbability)。他的伟大之处在于在1872～1875年间给出了熵的定量表达，1900年普朗克将它写成我们现在熟知的形式 S=k logW（图3）， 其中W应被理解为同体系热力学变量相恰的宏观状态数（W is the number of quantum states of a macroscopic system compatible with the thermodynamic variables prescribed for the system.[10]）。不过，这里有个误解。用在这里的W是德语概率Wahrsheinlichkeit的首字母，状态数和某个状态出现的概率是倒数关系，故此公式中的W是理解为状态数还是概率问题不是太大，只相差一个负号。后来出现的吉布斯（J. Williard Gibbs）熵、香农（Claude Shannon）的信息熵 （见下文），其定义都是基于概率的概念，所以都有一个负号。因为利用状态数有其便利的一面，为避免混淆，一些统计力学书中把熵公式写成 S=k logΩ的形式，用Ω表示同宏观状态相恰的微观状态数。这个熵公式的美妙之处在于，若体系的状态数或几率具有可分解性 （factorizability），这在经典热力学和古典概率中是得到满足的，则熵应有可加性，这是熵作为一个热力学的广延量必须具备的性质。考察这部分内容时，笔者有了“物理学唯赖天成”的感觉。熵公式是为了应付计算阶乘，factorial，的麻烦，被鬼使神差地通过近似引导到对数函数的形式上的。而经典概率的可分解性, factorizability, 恰恰通过对数函数保证了熵的可加性。奈何天意乎？

 

而这般得窥天机的工作，是要耗费心血甚至要以生命为代价的。玻尔兹曼的工作建立在原子论的基础上，而1900年前后人们还没有能力看到原子，对原子论的怀疑或责难也算情理之中的事情，这里面尤以马赫的名言 “Haben Sie mal Atom gesehen（您见过原子吗？）”为代表。1906年，饱受压抑之苦的玻尔兹曼自杀身亡。巨星陨落，为后人留下无限的哀思。80年后，人类终于能够从图像上分辨出单个原子。

图3 维也纳中央公墓树立的玻尔兹曼的胸像。

 

热力学长期被看作是一门普通物理课，对近代物理中的量子力学、固体量子论等同热力学的渊源却强调不足。许多人印象中， 普朗克是量子力学的创始人，实际上他把一生都献给了热力学（图4）。2008年，德国物理学会纪念普朗克诞辰150周年纪念文集之一的题目就是“献给热力学的一生（Ein Leben für die Thermodynamik）” (见文献［4］，p39)。爱因斯坦因对相对论、量子力学的贡献闻名于世，实际上他关于布朗运动和金刚石比热的工作已尽显大家风范，后者开启了固体量子论这门学科。热力学才是一门高深的、又要求修习者具有天分的学科！

 

有一种论断，认为提出量子论并非普朗克的本意，所以一直有“普朗克：违背自己意愿的革命家（Max Planck: Revolutionär gegen Willen? ）” 的说法[4]。不考虑意愿的问题，就具体的工作来说，普朗克从假定的熵与内能的关系式出发拟合黑体辐射公式（辐射能量密度分布对温度的依赖）确是神来之笔。记黑体辐射在频率 ν 处的单位体积平均能量为 Uν 假设

 

 

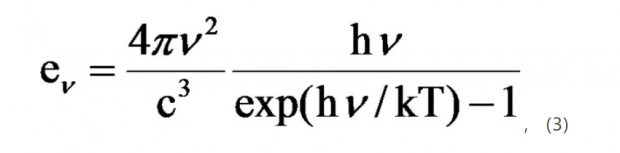
这个公式很好地拟合了黑体辐射的实验数据。这个公式公开几天之后， Kurlbaum就得出了h=6.65×10-34Js。这时的 “h” 就是一个常数，它的量子力学意义是后来被赋予的。注意，公式（3）同现在的黑体辐射公式相差一个常数2，因为那时人们没认识到光子有自旋，更不理解光子的自旋为1为什么意味着存在两种（左旋和右旋）而不是三种模式。有趣的是，1924年，玻色（S. N. Bose）推导黑体辐射公式就暗含了光子有两种（以上）模式[12]，所用方法就是玻尔兹曼曾采用的计算将N个全同粒子分配到不同状态上之可能状态数的那一套。

 

 

 

图5 维也纳大学摆放的薛定谔胸像。容易看出同玻尔兹曼塑像的相似性。是对师承关系的隐喻还是源于同样的维也纳设计风格？

 

 

热力学第二定律将熵推到了作为热力学系统演化方向判据的位置：对于一个孤立的体系，体系的熵恒增加。熵增加意味着系统可能的状态数的增加，因此直观上熵增加就和系统的无序联系了起来。但是，熵同无序度之间的关系却存在误解。所谓熵增加对应状态数的增加，但状态数是相空间里的概念，并不必然地同坐标空间里的、视觉上的从有序到无序的变化（图6）相一致。熵增加在坐标空间中可能表现有序来，比如一定条件下小水珠会聚集成大水珠。另一个值得注意的现象是，系统某个自由度上的熵的减小可能换来系统总熵的增加，但那个自由度上熵的减小所对应的有序，因为视觉上较明显容易让人误以为整个体系变得有序了。比如由棒状单元组成的系统，像类似细火柴棒的丝状液晶 (nematic liquid crystal)，水面漂浮的竹排（图7），夏天广场上躺着纳凉的人群，这些体系没有位置有序（positional order）但可以自发地表现出长程的取向有序（ long-range orientational order），因为沿着长轴方向的取向有序可以在横向方向上换来更大的活动自由，这显然是符合热力学第二定律的. 这种连江上放排的老乡都知道的事实，即体系一个自由度上熵的减小会换来其它自由度上熵的大增，却被一些科学家冠上了“熵驱动的有序（entropy-driven order) ”这样一个误导性的名称，实在匪夷所思。

 

 

 

 

熵这个概念虽然今天已被人们运用到了许多学科中去，但在关于热力学的文本中人们对熵感到生疏的历史痕迹依然还在。像玻尔兹曼常数，人们习惯用的物质比热，本质上都是熵。在相变和临界现象的实验研究中，常见人们测量比热却不从熵的角度深入讨论问题就是这种生疏感的表现。物理学研究固然需要以易测量的物理量来求得事实的佐证或应用的实施，但对于内涵的理解，还是应该建立在基础概念上。熵的概念是一个丰富的矿藏，笔者未能窥其奥秘之万一，且一篇短文也不足以描绘神龙之首尾。匆匆收笔，留待有机会时再论。

 

补缀

 

1. 所谓“普朗克”1923年访华一事一直困扰着我，期间我曾托人到南京寻找原始资料未果。本文付印以后，自然科学史所的朋友来信指出，1923年访华的“普朗克“应为Rudolf Alois Valerian Plank（1886－1973）。Plank出生于乌克兰， 后曾在Dantzig （原属东普鲁士，现属波兰）工业大学担任热学教授，在德国Karsruhe工业大学担任机械学教授，1956年曾任美国哥伦比亚大学客座教授。Plank 长期致力于热力学研究，1949年创办《制冷技术》杂志，其1925年获得Karsruhe工业大学教授职位所作的升职报告的题目就是“熵的概念（Begriff der Entropie）”。在一篇题为 “我们不可以忘却德国‘深度制冷之父’（Vergessen wir den deutschen “Vater des Tiefgefrierens” nicht!）”的文章（Tiefkühl Report 11 （2008） p. 8 ）中，我找到了这样的一句话: “他（Plank）那时甚至已经同中国有了联系（Und er knüpfte damals schon Verbindungen sogar bis nach China”），可算是Plank曾来华的比较可靠的证据。

 

再后来，冯端先生托人来信，指出他书中的 “I. R. 普朗克”，其中的“I”实际上德语Ingenieur（工程师）的首字母 （德国有在名字前加上Prof. Dr. Ing. 头衔的习惯），可能当时的文献就造成了讹错。可以这样猜测，Plank来华时的名帖可能是Prof. Dr. Ing. Rudolf Plank， 其全名被国人给理解成了 “I. R. 普朗克”。

 

关于 Rudolf Plank访华的细节，《物理》杂志2010后半年有一篇文章详细论述。

 

2012年，此文入选《物理》杂志四十年经典，笔者应邀专门撰写了一段回顾，照录如下：

 

Entropy 变成熵的考证

 

初学热力学，知道了熵这个概念，后来又学了entropy/Entropie，但对西文的Entropy如何转化成了中文的熵，倒也没当作一回事。然而。期间慢慢感觉到，从熵，即热温商，ΔQ/T，去理解entropy是有问题的，于是有了要理清entropy 概念如何传入中国的想法。读冯端先生《熵的世界》一书，中有“1923年，I. R.普朗克来中国南京讲学，著名物理学家胡刚复教授为其翻译时，首次将‘entropy’翻译成为‘熵’”一段。普朗克的字样易让人想起提出量子论的普朗克，但那人德语原名为Max Planck，且Planck传记中从未提及他来过中国一事。于是，我向刘寄星教授请教I. R.普朗克为何人，刘寄星教授让我找赵凯华教授《北大物理九十年》一书，发现那里有“濮朗克教授（是否Max Planck待考）与1923年5月29日至6月1日在北大理学院大讲堂和国立工业专门学校讲：‘热力学之第二原理及热温商（entropy) 之意义’，‘Nernst热论’……”的字样，可见赵凯华先生对此事也不知情。托朋友查南京的老档案，未果。后来，我同科学史所方在庆研究员说起此事，方在庆研究员用翻阅德国电话黄本的方法，检索发音接近普朗克的物理学家的姓名，找出了1923年访华的普朗克为Rudolf Alois Valerian Plank（1886－1973）。Plank出生于乌克兰，后曾在Dantzig （原属东普鲁士，现属波兰）工业大学担任热学教授，在德国Karsruhe工业大学担任机械学教授，1956年曾任美国哥伦比亚大学客座教授。Plank 长期致力于热力学研究，1949年创办《制冷技术》杂志，其1925年获得Karsruhe工业大学教授职位所作的升职报告的题目就是“熵的概念（Begriff der Entropie）”。后来，我在2008年的深度制冷杂志（Tiefkühl Report ）上找到了关于Plank的介绍，其中有“Und er knüpfte damals schon Verbingdungen sogar bis nach China（他那时甚至把关系建到了中国）”一句，算是Rudolf Plank来华的重要证据。冯端先生一书中的“I. R.普朗克”，应是当年的报导错把头衔 “Prof. Dr. Ing.” 中的Ing. (Ingenieur, 工程师) 当成名字造成的。我把这些内容报告给了刘寄星教授和赵凯华教授，他们觉得这件事算是有了着落。后来，刘寄星教授还专门委托首都师范大学研究历史的同仁翻出了1923年的老报纸，研究了Plank 1923年在中国的活动，结果发表在《物理》杂志2010年第8期上。至此， entropy如何变成熵的考证活动，终于尘埃落定。

 

关于entropy 如何变成熵的这段考证经历，让我有一个感慨，就是关于如何在中文语境中严格正确地表达和理解物理学，我们还缺的太多。像Rudolf Plank 这样被称为“深制冷之父 (Vater des Tiefgefrierens) ”的著名物理学家，我们竟然根本不知道此人且长期满足于不知道此人，说明我们的物理学，包括物理学研究和物理学教育，确实欠缺点儿什么。当然， entropy有比熵更多的内容，需要我们仔细体会。

 

——曹则贤 2012.1.19

 

2. 在Karl Popper的Unended Quest, Routledge, London (1992), 一书中， 有观点认为信息是负熵（information=negentropy），熵意味着缺乏信息（lack of information）， 不知道（nescience)。信息熵借用了物理学熵的概念，但似乎不应该当做一回事儿。

 

3. 著名的熵公式 S=k logW 是柏林大学热力学老师普朗克先写出来的。

 

4. 维恩1894年的文章“辐射的熵与温度” (Wilhelm Wien, Temperatur und Entropie der Strahlung, Annalen der Physik 288 (5), 132–165 (1894)) 应该是一篇物理学经典。在这篇文章中维恩指出，对于黑体辐射，ν/T是不变量。这篇文章对普朗克1900年的革命性工作有多大影响，不得而知。

 

注释

 

（1） 设想将一盆热水倾倒到一盆冷水中，此时刻体系是不好定义温度的。——笔者注。

 

（2） 确切地说应是内能U关于ST以及其它的共轭热力学量对 （比如电场E和电极矩P）作勒让德变换以后得到的恰当的热力学势，这排除了焓(enthalpy)这样的不含U关于ST的勒让德变换的一类热力学势。根据研究体系的不同，热力学势有很多。——笔者注。

 

（3） Emergent phenomenon目前被暂译呈展现象。关于这个问题，将来在请教相关专家后再另文讨论。——笔者注。

 

（4）为准备2008年夏季的量子力学系列讲座，笔者仔细地阅读了这两篇论文。不得不说的是，在仔细阅读了这两篇论文以后，我个人认为薛定谔推导波动方程时的跳跃可能依然是量子力学的硬伤。——笔者注。

 

（5） 笔者1984年秋开始学习量子力学课程，记得上来就是 ，完全不知道这方程还可以是凑出来的，也完全不知道这方程和理论力学课是一脉相承的，也不知道薛定谔自己时常按照经典的扩散方程来类比地看待他的方程。这门课是如何过的，我一直不能回忆起来。——笔者注。

 

参考文献

 

[1] R. Clausius, “Über verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie,” Poggendorffs Annalen, 125 353-400(1865).

 

[2] 冯端、冯少彤，熵的世界，科学出版社（2005）.

 

[3] 沈克琦、赵凯华(编)，北大物理九十年，北京大学出版社（2003）.

 

[4] 德国物理学会，Journal der Physik, März, (2008）.

 

[5] J. L. Heilbron, Max Planck, Hirzel (2006).

 

[6] 曹则贤，热力学系列讲座，中国科学院研究生院（2009）

 

[7] R. B. Laughlin, A Different Universe, Basic Books (2005).

 

[8] James P. Sethna, Statistical Mechanics: Entropy, Order Parameter, and Complexity, Oxford University Press (2006).

 

[9] D. Flamm, Ludwig Boltzmann and his Influence on Science, Studies in History and Philosophy of Science Part A, Vol. 14 (4), 255-278 (1983).

 

[10] N. E. Cusack, The Physics of Structurally Disordered Matter: an Introduction, Adam Hilger, Bristol (1987).

 

[11] 曹则贤，物理学咬文嚼字023: 污染掺杂各不同，《物理》，38卷5期，356－360（2009）.

 

[12] S. N. Bose, Plancks Gesetz und Lichtquantenhypothese，Z. Phys. 26, 178–181 (1924).

 

[13] Ervin Schrödinger, Quantisierung als Eigenwert Problem, Annalen der Physik 79: 361–376 (1926).

 

[14] Ervin Schrödinger, Quantisierung als eigenwert problem II, Annalen der Physik 79, 489–527 (1926).

 

[15] Graham Farmelo, It Must Be Beautiful: Great Equations of Modern Science, Granta Books (2002).

 

[16] Herbert Goldstein, Classical Mechanics, Addison-Wesley Publishing Company (1980).

 

[17] Claude Shannon, The Mathematical Theory of Communications，Bell System Technical Journal 27, 379-423, 623-656 （1948）.

 

[18] V. I. Arnold, Mathematical Methods of Classical Mechanics, 2nd edition, Springer-Verlag (1989).

 

[19] 汪克林，曹则贤，时间标度与甚早期宇宙疑难问题，《物理》，38卷（2009）(in press).

 

[20] D. Chowdhury, D. Stauffer, Principles of Equilibrium Statistical Mechanics, Wiley-VCH (2000).

 

注：本文为曹则贤著 《物理学咬文嚼字》第27篇，原题为《熵非商》。

 

 

版权说明：欢迎个人转发，任何形式的媒体或机构未经授权，不得转载和摘编。转载授权请在「返朴」微信公众号内联系后台。