撰文 | 倪忆（加州理工学院数学系教授）

 

前一段时间看到一个绳结魔术：

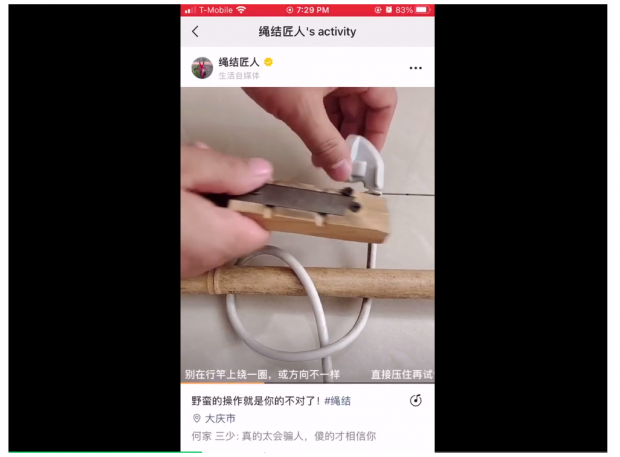
视频来源：“绳结匠人”视频号 [1]

 

同样内容的视频在这个号里有好几个，下面的评论很多都说是在骗人。是不是骗人，自己做一个实验就知道了。不过，虽然实验容易做，里面的原理一点儿也不简单。

 

首先，这里面电线的缠绕方式是有讲究的。比如说下图中最简单的这种，就不能用视频里面的办法把电线抽出来，只能采用原视频所说的“野蛮操作”，先把电线剪断，再抽出来，最后接上。

下图左边是视频里的缠绕方式。右边跟左边长得很像，但却不能够用视频里的办法抽出。左右两边有何不同呢？

上图左边，电线在棍子的下方穿过了两次。但一次是从前往后穿过，另外一次是从后往前穿过。因为两次的方向相反，所以实际上抵消了。这就是为什么我们可以把电线抽出来。

 

上图右边，电线在棍子的下方同样穿过了两次，但两次都是从后往前穿过，方向相同。所以我们没有办法把电线抽出来。

绿色箭头表示电线的走向，红色箭头表示电线从棍子下方穿过的方向

 

为了判断“电线能不能抽出”，我们可以定义电线相对于棍子的“环绕数”（linking number） [2]。我们数电线在棍子的下方穿过了几次：如果是从后往前穿过，就算作一次；如果是从前往后穿过，就算作负一次。把所有的正负一都加起来，得到的整数就是环绕数。第一张图里的环绕数是1，第二张图左边的环绕数是0，右边的环绕数是2。只有当环绕数是0的时候，电线才可以抽出。

 

那么，在环绕数是0的时候，有没有一定的规则让我们能抽出电线呢？答案是肯定的。以原视频为例，我们其实可以不必像他那样故弄玄虚，而是用下面视频里的办法来抽出电线。当然，这种方法过于朴实无华，没有原视频的戏剧性，就不可能有原视频那样的流量。

 

利用环绕数，我们可以进一步研究两股或者更多股绳子如何打结。从上古结绳记事开始，绳结就是中华文化里重要的符号。下图里的绳结是著名的“同心结”，在中国古代的婚仪里经常出现，文学作品里亦屡有提及。我们说的“结发夫妻”，“结发”指的就是成婚时男女各剪下一缕头发，结成同心样式的髻。唐代女诗人晁彩的《子夜歌》其一写道：“侬既剪云鬟，郎亦分丝发。觅向无人处，绾作同心结。”李白的诗句里也有“横竽宝幄同心结，半拂琼筵苏合香”和“悔倾连理枝，虚作同心结。”

同心结丨图源：http://www.handymariner.com/

 

无独有偶，同心结在当代欧美文化里也非常盛行。英语里同心结名为True Lover's Knot（真爱结），并用tie the knot（打结）来指代婚礼。实践中也经常会采用更复杂的结，不一定是上图中的同心结。至于东西方文化之间是否有相互影响，恐怕需要民俗学家的考证。同心结里面两段绳子彼此之间的环绕数是1。这里敲一下黑板，单身人士一定要好好练习，别打错结哦！

同心结式样的戒指丨图源：http://www.jamesavery.com

 

环绕数是一门叫做“拓扑学”的数学分支里面的概念，它最早是由德国的大数学家高斯定义的。

十马克钞票，上有高斯头像丨图源：www.worldbanknotescoins.com

 

巧合的是，高斯发现的环绕数公式跟电磁学里的安培定律和毕奥-萨伐尔定律有关，尽管高斯研究的并不是如何抽出电线。环绕数至今仍然在物理学里发挥着重要的作用。作者在大学普通物理课上曾经学过一个叫做AB效应（全称“阿哈罗诺夫-玻姆效应”）的物理实验。该实验证明了即使在磁场为零的区域，仍旧会存在磁效应。这个AB效应从数学上就可以用环绕数来解释。

 

德国物理学家冯·克利青（Klaus von Klitzing）因为发现量子霍尔效应而独享1985年诺贝尔物理学奖。加州理工学院的数学家巴里·西蒙（Barry Simon）在1983年率先用环绕数来解释量子霍尔效应，深刻地影响了相关领域的发展。（见《巴里·西蒙专访：重塑物理学的数学家》） 从量子霍尔效应开始，诞生了一个新的物理学领域，就是拓扑相变和拓扑物态的研究。这方面的工作对于新型材料和量子计算都有着重要的指导意义，著名华裔物理学家文小刚和张首晟在该领域作出过卓越的贡献。

 

2016年诺贝尔物理学奖授予拓扑相变和拓扑物态领域的工作，而同一年的诺贝尔化学奖授予分子机器设计与合成方面的工作。这两样获奖工作都跟环绕数有关：物理学奖的工作，正如前面所说，是量子霍尔效应的进一步发展。而化学奖得主合成了索烃（Catenane）和轮烷（Rotaxane），其中一个环状分子相对于另外一个分子的环绕数是1。

2016年诺贝尔物理学奖得主丨图源：诺奖官网

2016年诺贝尔化学奖得主丨图源：诺奖官网

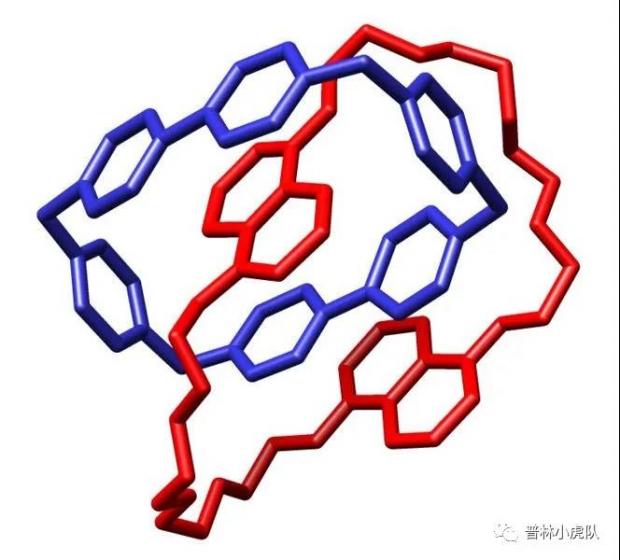
一个索烃分子的结构图 [3]，其中两个环状分子彼此间的环绕数是1

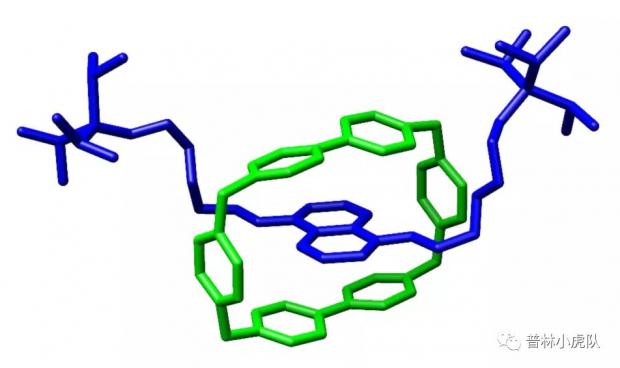
一个轮烷分子的结构图 [4]，其中绿色环状分子相对于蓝色分子的环绕数是1

 

研究DNA的时候也经常需要用到环绕数。众所周知，DNA分子是双螺旋结构。然而，下图那种常见的DNA雕塑其实是管中窥豹只见一斑，因为DNA的双链并不总是直的，而是有着复杂的自我缠绕和蜷缩。

中关村的DNA雕塑丨图源：中关村杂志

一张线性DNA的电镜照片 [5]

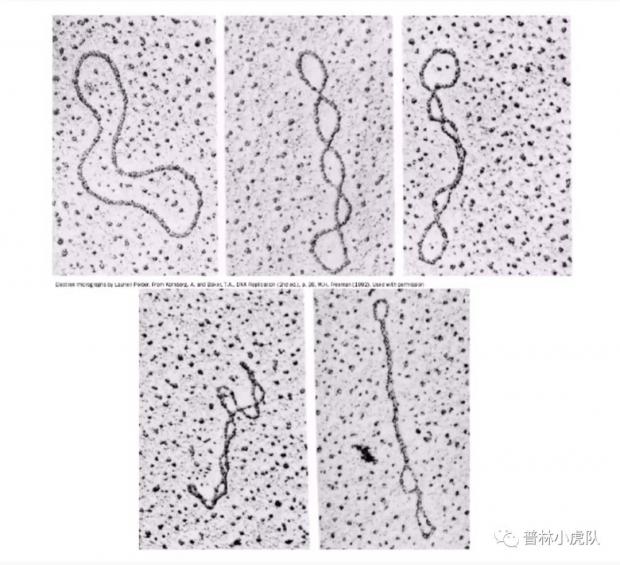
一些环状DNA的电镜照片 [6]

 

在DNA复制时，双链会局部展开为单链，每一段单链按照碱基互补配对原则合成互补的单链，最终形成两个DNA分子。可是，如果原来的DNA分子的缠绕和蜷缩过于复杂，那么无论从几何上还是从物理上都很难把两段单链无损地拆开，就像我们有时不能把电线从棍子下方抽出来一样。

如果两段单链之间的环绕数过大，就难以将它们拆开 [7]

 

对于这种情况，大自然提供的解决办法就是“野蛮操作”：先切断DNA双链上的一股或者两股，让另外一股或者两股DNA穿过此缺口，然后再接上缺口。参与这个过程的一类酶叫做拓扑异构酶 (Topoisomerase)，由华裔生物化学家王倬率先发现。这个过程通常会改变两条单链之间的环绕数，所以环绕数成为研究DNA结构和拓扑异构酶所必需的概念。

美国国家科学院院士，台湾“中央研究院”院士，哈佛大学教授王倬丨图源：“中央研究院”网站

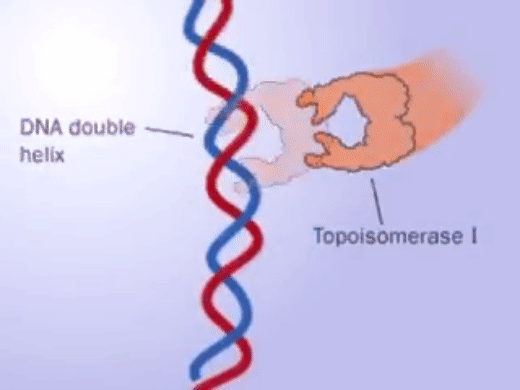
第一型拓扑异构酶的作用，剪断一股单链并重接 [8]

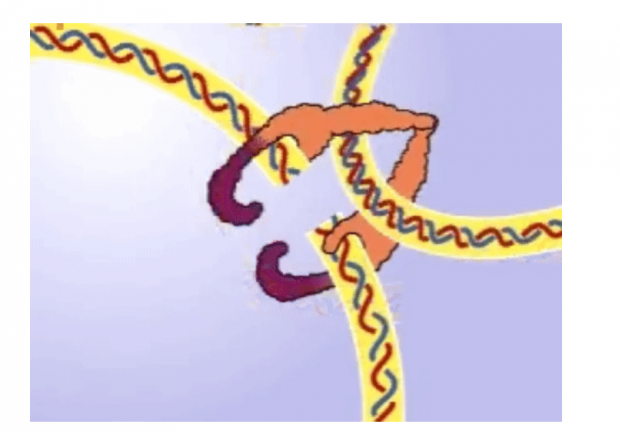
第二型拓扑异构酶的作用，剪断双链并重接 [8]

 

拓扑异构酶在DNA复制和转录过程中起到了重要作用，如果能够抑制拓扑异构酶，就能有效阻碍这一过程。很多药物就是利用这一原理来产生疗效。常见的诺氟沙星 (norfloxacin，即氟哌酸)、环丙沙星 (ciprofloxacin)、左氧氟沙星 (levofloxacin)、莫西沙星 (moxifloxacin) 等抗生素就是这样抑制细菌的繁殖。一些用于癌症治疗的药物也是通过干扰拓扑异构酶来抑制癌细胞生长，甚至使癌细胞死亡。这类药物包括伊立替康 (irinotecan)、拓扑替康 (topotecan)、依托泊苷 (etoposide)、替尼泊苷 (teniposide) 等等。[9]

 

绳结并不仅仅是好玩的魔术道具，也不止是文化上的象征。在科学家们的努力下，其中涉及的科技已经改善了我们的生活，并将给我们带来一个更为光明的未来。

中国结丨图源：人民网

 

注释

 

[1] 因为微信本身的限制，无法链接到原视频。所以我们将原视频录下后重新上传。

 

[2] 姜伯驹院士在《绳圈的数学》一书中将linking number翻译为环绕数。另外一个拓扑学概念winding number也经常翻译为环绕数。这两个概念本质上是一样的，本文中不加以区别。

 

[3] Peter R. Ashton, Christopher L. Brown, Ewan J. T. Chrystal, Timothy T. Goodnow, Angel E. Kaifer, Keith P. Parry, Douglas Philp, Alexandra M. Z. Slawin, Neil Spencer, J. Fraser Stoddart and David J. Williams. The self-assembly of a highly ordered [2]catenane. Chemical Communications, 1991, 634–639.

 

[4] J. A. Bravo, F. M. Raymo, J. F. Stoddart, A. J. P. White, D. J. Williams. High Yielding Template-Directed Syntheses of [2]Rotaxanes. Eur. J. Org. Chem. 1998, 1998 (11): 2565–2571.

 

[5] B. K. Chakrabarti, D. J. Chattopadhyay and A. N. Ghosh. Vibriophage D10 contains non-permuted DNA with cohesive ends. Journal of General Virology Volume 74, Issue 12, 1993.

 

[6] Arthur Kornberg, Tania A. Baker. DNA Replication, 2nd edition, University Science Books, (2005).

 

[7] DNA supercoiling and topoisomerase, https://www.youtube.com/watch?v=yMKGzq5c8i4

 

[8] Topoisomerase 1 and 2, https://www.youtube.com/watch?v=EYGrElVyHnU

 

[9] 维基百科，Topoisomerase inhibitors.

 

本文经授权转载自微信公众号“普林小虎队”。