还有人分不清咖啡杯和甜甜圈？数学家说，还真有！-返朴的财新博客-财新网

许多朋友听说过关于“咖啡杯和甜甜圈是同一回事”的论述，也有许多朋友对于拓扑的最初印象也来自于此。但是抛开这个模糊的表述，我们有没有办法严格地去定义这一点呢？这就要用到我们今天的话题“同调论”的观点了。

撰文 | Kelsey Houston-Edwards

翻译 | xux

审校 | C&C

起初，拓扑学似乎是数学中一个异常不精确的分支。这是一门研究黏糊糊橡皮泥的学科，它的研究对象能够无限地弯曲、拉伸和压缩。但是也有一些限制：不能在形状中创造或破坏洞。(一个古老的笑话：拓扑学家分不清咖啡杯和甜甜圈，因为它们都有一个洞。）虽然这似乎与代数的严谨相去甚远，但一个叫做同调的强大想法帮助数学家连接了这两个世界。

发明同调论起初是为了严格计算出“洞”的数量。同调论为数学思想提供了框架，让我们能够用一种新的方式来分析数据中的形状。

“洞”这个词在日常用语中有很多含义——泡泡、橡皮筋和碗的“洞”各不相同。数学家感兴趣的是一种特殊类型的洞，这种洞可以被描述为一个封闭且中空的空间。一维的孔看起来像橡皮筋。橡皮筋的曲线是封闭的（不像一根松散的绳子）和中空的（不像一元硬币的周界）。

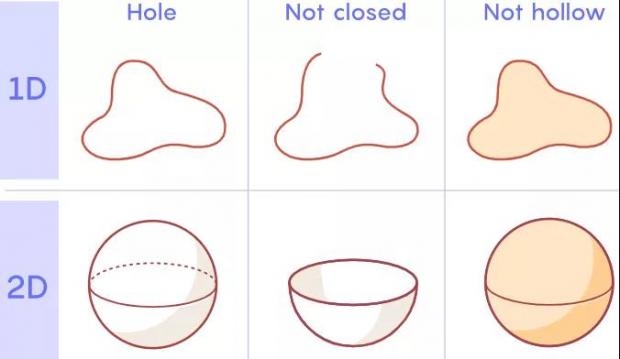
洞、非封闭、非中空

将这个逻辑扩展下去，那么二维洞便是一个空心球。数学家们正在寻找的这种洞，是像篮球那样封闭且中空的，而不是像碗或保龄球上的洞。

但是数学是严谨的，虽然用这种方式思考，能够让我们直观地想到橡皮筋和篮球，但它还不够精确，不足以作为一个数学定义。例如，它不能清楚地描述更高维度的洞，你也不能编程让计算机区分封闭空间和中空空间。

密歇根州立大学的何塞·佩雷亚说：“对于洞，没有一个好的定义。

相反，同调从物体的边界推断出物体的洞，这是一个更为精确的数学概念。想要研究物体上的洞，数学家只需要知道物体边界的信息。

形状的边界是其外周上点的集合，边界总是比形状本身低一个维度。例如，一维线段的边界由两端的两点组成。（点是零维的。）实心三角形的边界是由一维边线组成的空心三角形。同样，实心棱锥的外边界是空心棱锥。

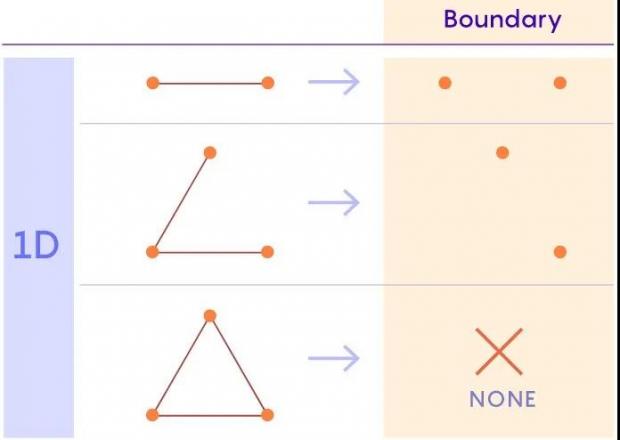
不同维度的形状的边界（boundary）

如果将两条线段粘在一起，它们相交的边界点将消失。边界点就像悬崖的边缘——它们几乎要从直线上掉下来。但是当你将这些线连在一起时，边界上的点就会安全地呆在中心。另外，这两条线总共有四个边界点，但当它们粘在一起时，生成的形状只有两个边界点。

如果再加一条边，让结构封闭起来，形成一个空心三角形，那么边界点就消失了。组成三角形的三条边的每个边界点与另一个边界点两两相消，空心三角形没有边界。因此，每当一组线形成一个圈时，边界就不复存在。

一个环（loop）绕回到它的起点会圈起来一片区域。但只有当环包围区域是空的时，才能称之为一个洞（hole），就像橡皮筋一样。画在纸上的圆形成一个环，但它不是一个洞，因为中心被填满了，这个圈是二维区域的边界。

因此，洞具有两个重要且严格的特征。首先，洞没有边界，因为它是封闭的。第二，洞不是其他东西的边界，因为洞本身必须是中空的。

这个定义可以扩展到更高的维度。二维实心三角形有三条边。如果将几个三角形连接在一起，一些边界边就会消失。当四个三角形排列成一个棱锥时，每一条边与另一条边相消。所以棱锥的面没有边界。如果棱锥是空心的，那么，它就不是一个三维实体块的边界，这时它就形成了一个二维洞。

为了在一个特定的拓扑图形中找到所有类型的洞，数学家们建立了一个叫做链复形的东西，它为同调论搭起了框架。

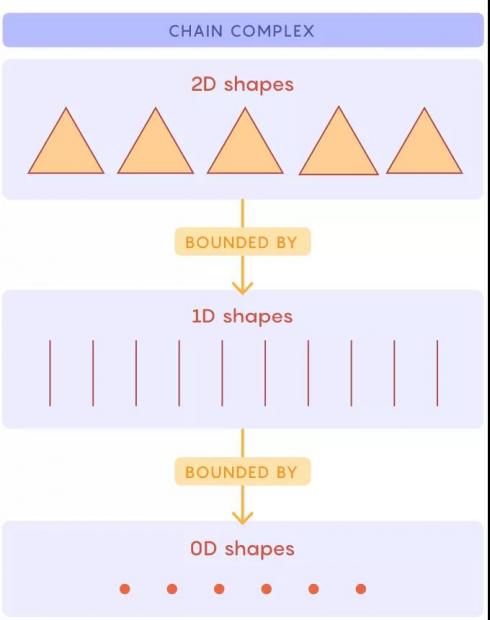
链复形

许多拓扑形状可以通过把不同尺寸的部分粘在一起形成。链复形是一个图表，它给出了一个几何图形的装配说明。图形的各个部分按维度分组，然后按层级排列：第一层包含所有点，下一层包含所有线，依此类推。(还有一个空的第零级，它只是作为基础。）每一层都通过箭头连接到下面的一层，这表明它们是如何粘合在一起的。例如，实心三角形连接到构成其边界的三条边。

数学家从链复形中提取图形的同调，链复形提供了有关形状组成部分及其边界的结构化数据，这正是描述每个维度上的洞所需要的。使用链复形时，查找10维洞和一维洞的过程几乎相同（只是其中一个比另一个更难可视化）。

同调的定义足够严格，计算机可以用它来寻找和计算洞的数量，这有助于建立数学中通常需要的严格性。它还允许研究人员将同调用于越来越流行的用途：分析数据。

这是因为数据能够可视化为浮在空间中的点。这些数据点可以表示物理对象（如传感器）的位置，也可以表示抽象空间中的位置（如食物偏好的描述），附近的点表示具有相似味觉的人。

为了从数据中产生图形，数学家在相邻的点之间画线。当三个点靠得很近时，它们被填充成一个实心三角形。当大量的点聚集在一起时，它们会形成更复杂、更高维的形状。填充数据点会给它们带来纹理和体积——从这些点创造出一个图像。

同调将这个模糊形状的世界转化为严格的代数世界，代数是研究特殊数值结构和对称性的数学分支。数学家在同调代数领域研究这些代数结构的性质。从代数中，他们间接地了解到有关数据的原始拓扑形状的信息。同调有很多种，它们都与代数有关。

“同调是一种常见的结构。麻省理工学院的玛吉·米勒说：“关于它，我们知道很多代数知识。”

同调提供的信息甚至可以解释数据的不精确性：如果数据只是稍微移动，洞的数量应该保持不变。当处理大量的数据时，这些洞可以显示出重要的特征。例如，时变数据中的循环可以表示周期性。其他维度中的洞可以显示数据中的簇（cluster）和空缺（void）。

宾夕法尼亚大学的罗伯特·格里斯特说：“真正的推动力是要有一种鲁棒性的方法，能够从数据中提取出定性特征。这就是同调带给我们的。”

本文经授权转载自微信公众号“中科院物理所”，原题目为《孩子分不清咖啡杯和甜甜圈，竟是因为......》。

原文链接：https://www.quantamagazine.org/how-mathematicians-use-homology-to-make-sense-of-topology-20210511/

话题：