如果将传统流体力学形容为一个江湖，N-S方程无疑是这个江湖最伟大的传说，只可惜这本“旷世秘籍”没有人能解开。于是流体江湖的三位大佬——雷诺、布辛涅司克和普朗特各自使出了自创的神功“雷诺平均的N-S方程”、“涡粘性假设”以及“混合长度理论”，将无法求解的N-S方程劈开了一个口子，从而开启了计算流体力学百年的RANS时代。

而近三十年来，尤其是进入新世纪以后，一种基于LBM的CFD方法慢慢走入大众的视野，无论是思想、方程还是实际操作过程都和传统CFD完全不同，甚至有传统CFD大佬直呼“It’s a magic”。随着LBM在工业领域的大放异彩，人们开始关注LBM的历史和今天。相对于N-S方程，LBM更像是流体力学的另一个江湖。

撰文 | 卢比与钢蛋

01

LBM中的L才是源头？

LBM（Lattice-Boltzmann Method）中文译为“格子玻尔兹曼方法”，自然以玻尔兹曼输运方程和麦克斯韦-玻尔兹曼分布为根基，不过在这个名字中，首当其冲的“格子”二字，才是LBM几十年发展的源头。而要问“格子”到底是从哪里来的，则必须从LBM的前世老祖——元胞自动机（cellular automata，缩写为CA）说起。
 

自动机，顾名思义就是自己可以动的机器，比如鲁班造的木鸢、孔明先生的木牛流马（手动狗头）。从计算理论上来说，自动机指的是一种抽象的自行式计算设备，自动遵循预定的操作顺序。

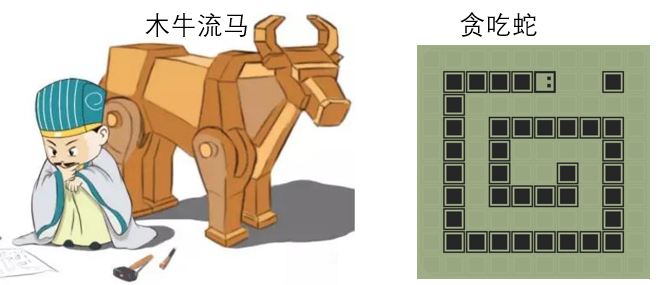
而元胞自动机指的是有一组规则的元胞（或格子），每个元胞都有某些状态（比如白或黑），当分配好初始的状态和演变规则后，下一个时刻元胞的状态由前一时刻的状态和周围元胞的状态确定，类似于我们玩过的贪吃蛇游戏。元胞自动机天然是一种时空离散的计算模型，其概念最早由斯坦尼斯拉夫·乌拉姆（Stanislaw Ulam）和冯·诺依曼（Von Neumann）于1940年代提出。他们当时在美国洛斯阿拉莫斯国家实验室工作，后来许多LBM领域的先驱也曾研学于此。

02

当格子遇见流体力学

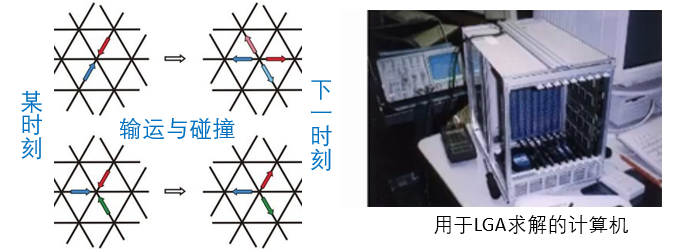
元胞自动机的概念催生了一些应用，比如细胞生长、沙丘堆积、城市发展的预测等等，其特点是使用微观粒子的时空积叠来描述宏观现象。而在流体力学领域，最初的应用典范便是格子气自动机（Lattice Gas Automaton，缩写为LGA）。格子气自动机使用布尔变量表示流体粒子在空间格子上的存在与否。在格子气自动机中，流体粒子存在于这些格子上，并严格按照格线迁移或者碰撞。这些粒子的演化只与自身状态和相邻粒子相关，因此可以方便的进行分区计算。而粒子的有无仅用0和1便可表述，不存在迭代的收敛问题。这与传统求解流体问题的思路大相径庭而又容易理解，当时这种方法风靡一时，甚至被誉为划时代的方法而登上了华盛顿邮报的头版，如同一入江湖便风头无限的少侠。

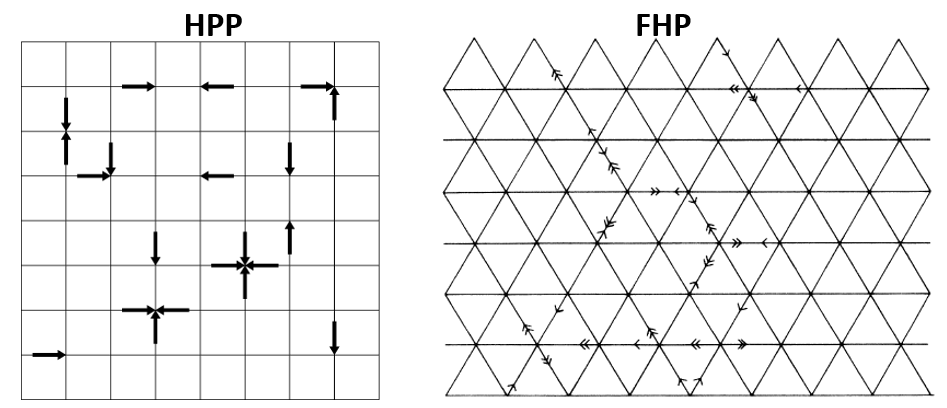
1972年，法国学者J. Hardy，Y. Pomeau和O.de Pazzis提出了第一个LGA模型，即HPP模型；1986年，U. Frisch，Y. Pomeau和美国学者B. Hasslacher提出了一个对称度更高的正六边形的LGA模型，即FHP模型，该模型成功的恢复了不可压缩N-S方程。而在Physical Review的125周年纪念专刊上，这篇文献也成为唯一入选的流体类文章。

少侠的出场虽然霸道，可是想要成为大侠尚需时日。随着方法的深入研究，人们发现LGA也有其天生的缺陷。对于湍流问题，LGA由于自由度（速度方向的数目）太低难以精确描述；而布尔运算又在局部带来了明显的数值噪声；更重要的是，通用计算机已朝着浮点运算的方向迅猛发展，只进行布尔运算则效率很低，人们不得不专门研制硬件。

03

LBM的雏形

为了应对LGA的种种缺陷，1988年McNamara和Zanetti从分子混沌的假设（忽略分子之间的相关性）出发，把LGA中的布尔运算替换成实数运算，粒子不再是0或者1，而演化为大神玻尔兹曼的分布函数f，并用玻尔兹曼输运方程代替了LGA的演化方程，叩开了格子波尔兹曼方法的大门。1989年，Higuera和Jimenez又引入平衡态分布函数feq简化了碰撞算子。

随后，LBM的发展迎来了华人之光。1991年，陈十一、陈沪东以及J.M.V.A. Koelman等学者分别独立提出了基于BGK单松弛模型将碰撞算子线性化的思路，即以控制趋近平衡态快慢的方式简化碰撞算子；而后，钱跃竑和陈沪东等学者又分别基于不同形式的格子和BGK模型，并使用麦克斯韦-玻尔兹曼分布来代替平衡态函数feq，并恢复了N-S方程。从此以后LBM开启了从少侠走向大侠的武学探索之路。

值得一提的是，上述方法源自于1954年Bhatnagar、Gross和Krook为简化玻尔兹曼输运方程而提出的碰撞间隔理论，又被称为格子BGK模型（即LBGK）。看来想要成为一代武学大师，还是需要旁征博引，啥武功都要会一点。

04

从LBM到流体力学

相对于LGA，LBM有两个巨大的优势：

在方程左侧利用统计函数消除数值噪声

在方程右侧使用碰撞算子的连续函数代替离散的碰撞规则

于是，LBM在速度分布函数和LBGK的加持下，就如同武林高手打通了任督二脉一样，展现了巨大的优势和潜力。

在LBM方法中，速度分布函数f依赖于位置与时间，因此在传统力学（物理量是位置和时间的函数）框架下，f依然是个连续的量——这也是它在宏观框架下亦能代表流体运动的基本依据。同样，由于f同时包含了位置、速度、时间的信息，而压力、密度等宏观变量通常只与位置和时间相关，因此如果对微观速度进行积分而移除其依赖性，即可得出各类宏观变量。

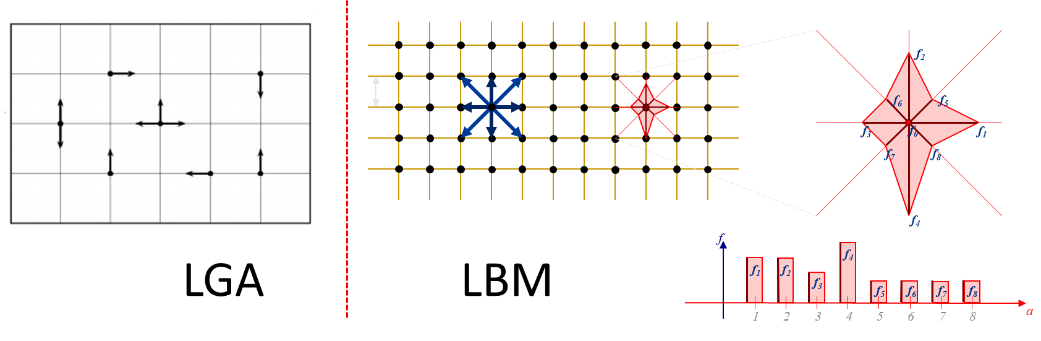
如下图所示，如果对分布函数、粒子质量及微观速度等的组合进行统计，则可得出宏观的密度、动量和能量。压力是粒子动量的体现，而温度被粒子动能表征，宏观速度则最直接，它是微观速度的期望——这些参数都可由移除微观速度依赖性的积分得出。LBM表面上看还是离散的方程，却有连续的属性——因此它一定程度上也具有欧拉以及N-S方程求解器的特质，相比LGA更为贴近于传统理解的流体力学。

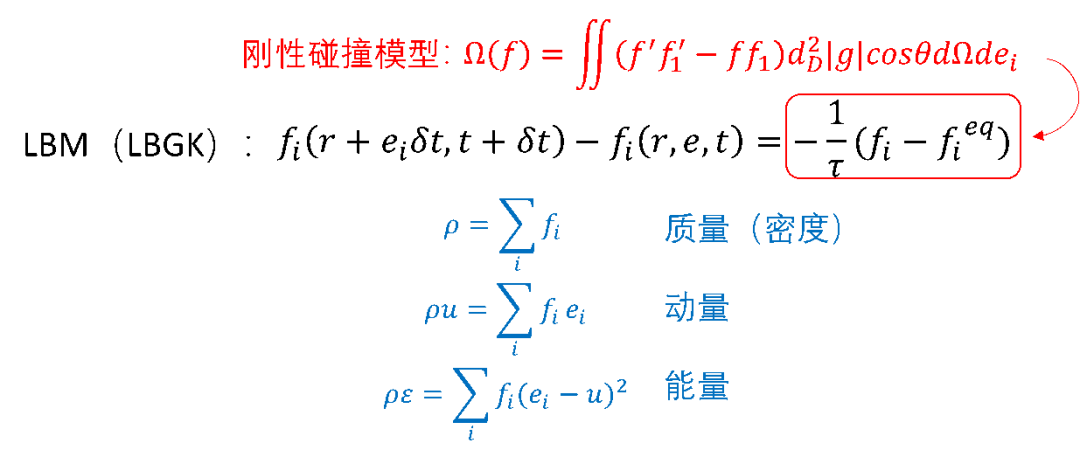
对于被LBGK所代替的碰撞项，也具有丰富的内涵——人们虽然不再纠结于粒子之间的相互作用力与碰撞方式，而是把它简化为刚性碰撞，但即便是刚性碰撞，也需要复杂的积分才能完成，而LBGK完成了碰撞算子的线性化。另外，LBGK描述了原始碰撞的零阶物理过程，这也意味着，如果想使用LBM求解复杂本构关系的物质，只需要修改碰撞项即可。

05

从LBM到CFD

从LBM到流体力学，仿佛郭少侠南下中原之后，跟随洪七公学习降龙十八掌。理论上降龙十八掌是天下第一刚猛的武功，可是郭少侠使出来效果如何，那就要去真正的江湖上试一试了。LBM从理论上搭建了微观速度分布函数和宏观物理量之间的关系，那么LBM究竟如何在计算流体力学的领域施展自己的抱负呢？相对于传统CFD的求解过程，基于LBM的CFD可谓是大道至简，用尽全身的力气打出去这一掌就可以了。

如上图所示，LBM的实施流程为：首先对全部格子的流场进行初始化，然后施加粒子的输运和边界条件算出中间过程的分布函数f*，而后求出密度和宏观速度，再计算此状态下的平衡态函数，最后施加粒子的碰撞，得出更新的速度分布函数f，此后就是循环迭代，直至计算结束。LBM凭借着其独特的技术优势在学术界和工程领域得到越来越多的关注。不过，也总给人感觉有点“根不正，苗不红”，正如大漠的人们都以为郭靖是个落难的孩童，却不了解郭靖乃是梁山好汉的后代。接下来我们就从统计物理出发重新推导LBM，为其正名。

06

LBM江湖的上古大神

19世纪中期，气体动理论的主要奠基人克劳修斯（Clausius）、麦克斯韦（Maxwell）和玻尔兹曼（Boltzmann）三人引进了统计概念，将宏观理论和微观基础联系了起来。1902年，Gibbs（吉布斯）把Maxwell和Boltzmann所创立的统计方法发展为系综理论（Ensemble Theory），使原来仅适用于气体的理论，推广到气体、液体和固体，并发展为今天的统计力学。

玻尔兹曼输运方程（Boltzmann Transport Equation，简称BTE或BE）诞生于1872年，而LBM则于1990年代左右由LGA发展而来，不过LBM诞生之初时，并没有跟连续的玻尔兹曼方程建立关联。后来人们逐渐认识到此问题的重要性——即从统计物理的角度重新审视并构造LBM。如下图所示，针对玻尔兹曼输运方程，首先使用BGK模型将碰撞算子线性化，然后在指定坐标系下进行时空离散得出LBGK方程，最终对平衡态函数进行泰勒展开并略去高阶项，即可得出LBM的控制方程以及各项参数。

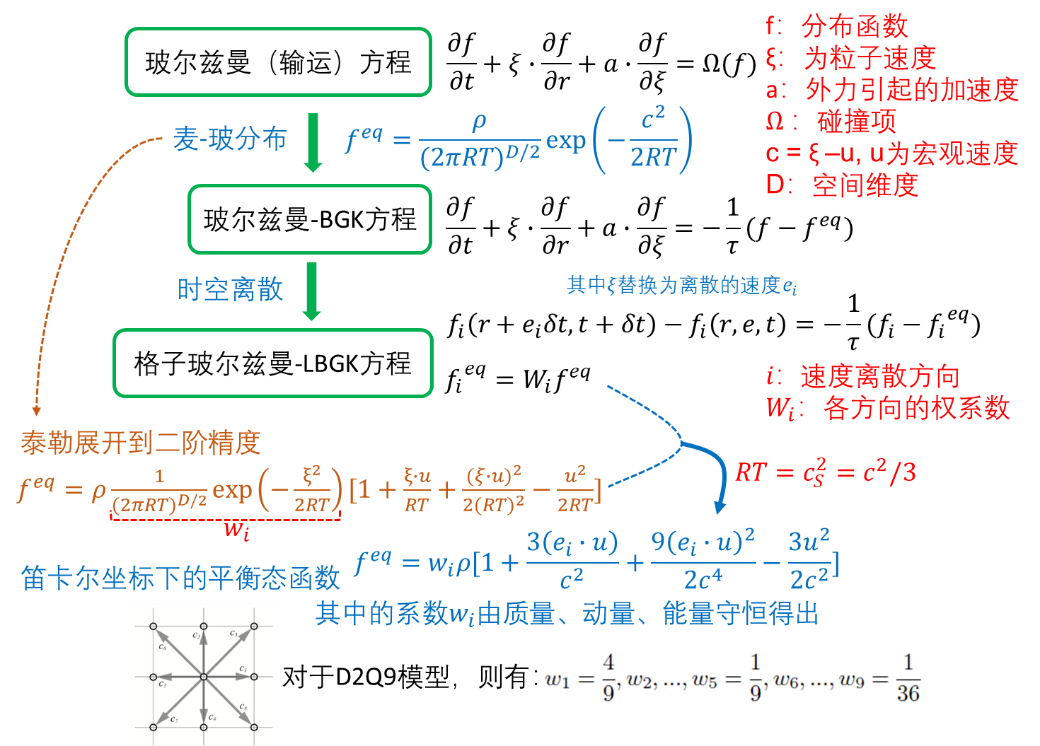
通过上述的推导，可以发现LBM是简化玻尔兹曼方程的一种特殊离散形式。由此，LBM终于找到了自己名正言顺的身份，有了各位上古大神的坐镇，加上近几十年来，华人科学家的巨大贡献，LBM也终于开宗立派，创建了属于自己的江湖。

结语

LBM方法从最初的低雷诺数、不可压缩流动的计算，历经日复一日的修炼升级，多年以后俨然自成体系，形成了另一个江湖。不过相比于公认的“旷世秘籍”N-S方程，人们对LBM能否反映真实的流体世界一直心存怀疑。本公众号将在后续推送更多的文章，揭示LBM闯荡流体江湖的心路历程，敬请期待。

本文经授权转载自微信公众号“LBM与流体力学”。