撰文 | 张江（北京师范大学系统科学学院）
 

2020年以来，人类社会的发展仿佛呈现出一条全新的轨迹：新冠肺炎疫情、极端天气、俄乌冲突、股市熔断、经济停滞、粮食危机，这些百年罕见的天灾人祸、重大事件集中、频繁地发生。与此同时，以人工智能、区块链、元宇宙等颠覆性技术为代表的高科技产业还在不遗余力地加速推进着。人们乐观地以为新的问题只有通过新的技术变革才能解决，但其实每一项新的发明都有可能引发新的问题和焦虑。人们不禁要问：这些意味着什么？这个疯狂的世界将要奔向何方？

要回答这一系列问题，应对人类百年未有之大变局，就必须站在一个全新的视角上进行系统性的思考。这一全新视角首先需要我们抛开所谓的“学科”的狭隘局限，将古今中外各个学科的知识统合起来；其次，它既让我们能站在全球的宏观视角把握大的发展趋势，又能深入细节，给出精细微妙的处理方案；另外，它还要求我们必须认识到所有这些问题都并非彼此孤立的，其背后存在着统一性。总之，我们需要一个新兴的学科作为思维的脚手架，帮助我们理解这个复杂的世界。

复杂科学（Complexity Science）无疑将承担起历史的重任。这门从20个世纪90年代发展起来的新兴学科试图采用跨学科的方法，研究各类复杂系统背后的统一规律。尽管它还很年轻，还没有一个普遍公认的概念体系和学科框架，但是它的跨学科范式、多尺度的研究视角以及整体论的、普遍联系的世界观，足以让它担此重任。

Complexity，Mitchell Waldrop，Simon & Schuster, 1992

早在1977年，著名化学家、统计物理学家伊利亚·普利高津（Ilya Prigogine）就凭借“耗散结构论”这一复杂科学的开创性理论成果获得诺贝尔化学奖。时隔近50年，复杂科学于2021年再次受到了诺贝尔奖的青睐，三名科学家分享了诺贝尔物理学奖，他们最突出的贡献是提出了普适性的手段，并将其应用到全球气候突变这样的重大问题上面。

复杂科学的研究对象是各式各样的复杂系统。那么，何为复杂系统？让我们举数例说明。

椋鸟是一种生活在欧洲的鸟，身长约22厘米，也就一个巴掌大小，但它们经常会集合形成规模庞大的鸟群，像一只巨大的水母飘浮在巴黎上空。椋鸟群飞翔时井然有序，彼此不会发生碰撞；而当规模庞大的鸟群朝埃菲尔铁塔飞去时，又会灵活地分裂成两个新的鸟群，分别从铁塔的两侧绕过，然后重新会合到一起。这种由椋鸟构成的群体就是一个典型的复杂系统，它们不是孤立的鸟，而是通过相互协调形成了一个庞大的整体。

另一个例子是路网。很多人都有在城市中开车的经验：每天清晨，当你开车行驶在公路上时，其实就在和路网上所有汽车所构成的复杂系统互动。每辆车都在跟随着前一辆车，即使在没有发生交通事故的情况下，只要车流密度很大、车速很快，一辆车的猛然刹车就有可能造成后续车辆的大堵塞——第一辆车的减速导致了后续车辆的减速，后续车辆的减速又会导致再后面的车辆减速，当这些减速连接到一起，就有可能形成由减速构成的“驻波”，像水面上的涟漪一样顺着路网传播开来。车流、路网的相互作用也会形成一个彼此密切相关的复杂系统。

并非由车辆事故引起的“幽灵堵塞”（phantom traffic），图源：TED-Ed. Benjamin Seibold: What is phantom traffic and why is it ruining your life?第三个例子是蚂蚁。蚂蚁在通过相互作用形成一个整体时展现出了非凡的智慧，如蚁群可以通过信息素来完成彼此之间的相互作用，从而在多条巢穴和食物之间的搬运路径中选择最短的一条。蚂蚁间的互动以及蚂蚁和环境中的信息素的相互作用形成了一个复杂系统。

由此可见，所谓的复杂系统就是由大量的单元相互联结、相互作用形成的统一的整体，这个整体表现出一定的奇妙属性，例如鸟群的灵活适应和整齐划一、交通流系统中的迟滞现象形成的“驻波”以及通过蚂蚁与信息素相互作用形成的最短路径。无论是鸟群、“驻波”还是最短路径，它们都不能被还原为某一只鸟、某一辆车以及某一只蚂蚁的属性。

复杂系统中存在着很多异常复杂且有趣的宏观现象和规律，例如蚂蚁的最优觅食路径以及黏菌的最优输运网络，而这些现象和规律都很难用其构成单元的特性加以解释，我们把这类现象称为“涌现”。复杂科学就是要研究这些不同的复杂系统丰富多彩的涌现现象背后的共同规律。用亚里士多德的一句话来概括，涌现现象即“整体大于部分之和”。它的意思是，当若干个体组合形成一个庞大的群体时，这个群体总会出现一些新的属性、特征、行为和规律，而又无法简单地归结到每个个体之上。复杂系统中普遍存在着涌现现象，但是涌现并不一定限于复杂系统中。

日常生活中最典型的例子是城市中的霓虹灯。我们都知道，城市中很多大楼和商店到了夜晚都会亮起霓虹灯。而所谓的霓虹灯，无非就是一堆小灯泡在闪烁，不停地变换颜色。但当你退后一步，就会看到由很多的小灯泡组成的霓虹灯整体呈现出图案或文字，且它们无法被还原到每个单独的灯泡上。每个灯泡的闪烁似乎都是无意义的，你只能通过它们形成的整体来解读它的意义，这个整体的图案或者文字就是一种涌现属性。

进一步，集体涌现的属性或规律可以反过来作用到微观个体身上。例如，近年一些互联网巨头争先恐后地收购和投资一些小型创新企业，从而搭建自己的“生态系统”，实际上就是在尝试利用涌现属性对个体的反作用这一规律。这种趋势不仅局限在互联网行业，很多国家的政府和地方部门也在主动培育产业生态，希望获得系统的力量加持。因为，随着势单力薄的个体聚集形成有活力的复杂系统，系统涌现出的特征会反过来给系统中的个体都带来好处。比如，系统内大大小小的公司会获得更稳定的客源、更低的成本和更高的收入，相较系统外的公司有了比较优势。

然而，复杂系统之间是如此不同，涌现现象又是如此丰富多彩，我们应如何寻找其共有的规律呢？答案是：建立不同复杂系统之间的类比。用一句比较文艺的话来说，就是寻找不同复杂系统彼此之间“遥远的相似性”。

每当乘坐夜晚的航班时，我都会选择一个靠近舷窗的位置。这样，我就能清晰地观察到飞机即将降落时舷窗外那座灯火通明的城市：一条条纵横交错的街道仿佛一条条毛细血管，公路上奔跑的汽车仿佛血管中的红细胞，所有的毛细血管相互缠结、连向城市的中心——这里仿佛是城市的心脏。总之，城市真的可以让我感受到它的“呼吸”和“脉搏”，它就是一个活生生的有机体。城市交通和人体血流是处于不同尺度、完全不同的复杂系统，前者的构成单元是车辆，后者的是细胞。上文中的类比却让我们清晰地看到了二者“遥远的相似性”，比如街道网络和血管网络具备非常相似的复杂联结模式，它们分别对城市的运转和人体的代谢起到了非凡的作用。这种相似性是寻找复杂系统背后共性的出发点。

科学界有一种明星生物——黏菌，它实际上是一个由大量可以独立自主地在环境中爬行的单细胞生物体——阿米巴虫构成的“超级生物体”。一旦这些阿米巴虫在多处找到了食物，它们就开始修建一条条类似“高速公路”的管道将食物联通起来——这一切在显微镜下清晰可辨。更让人惊奇的是，黏菌修建的“高速公路”竟然可以跟人类的高速公路网相媲美。2010年，日本东京大学的一个实验小组就利用黏菌做了一个神奇的实验。他们首先将整个东京市以及周边36个城市的地图等比例缩进实验室的培养皿中，其长度大概只有20厘米。然后，他们在地图上东京市附近的主要城市的位置上放上了阿米巴虫爱吃的食物，再把黏菌放到东京市的位置上。一天之后，当实验人员再次打开培养皿时，他们惊奇地发现，一张完整的高速公路网络刚好将周围的几个城市和中心的东京市联通到了一起。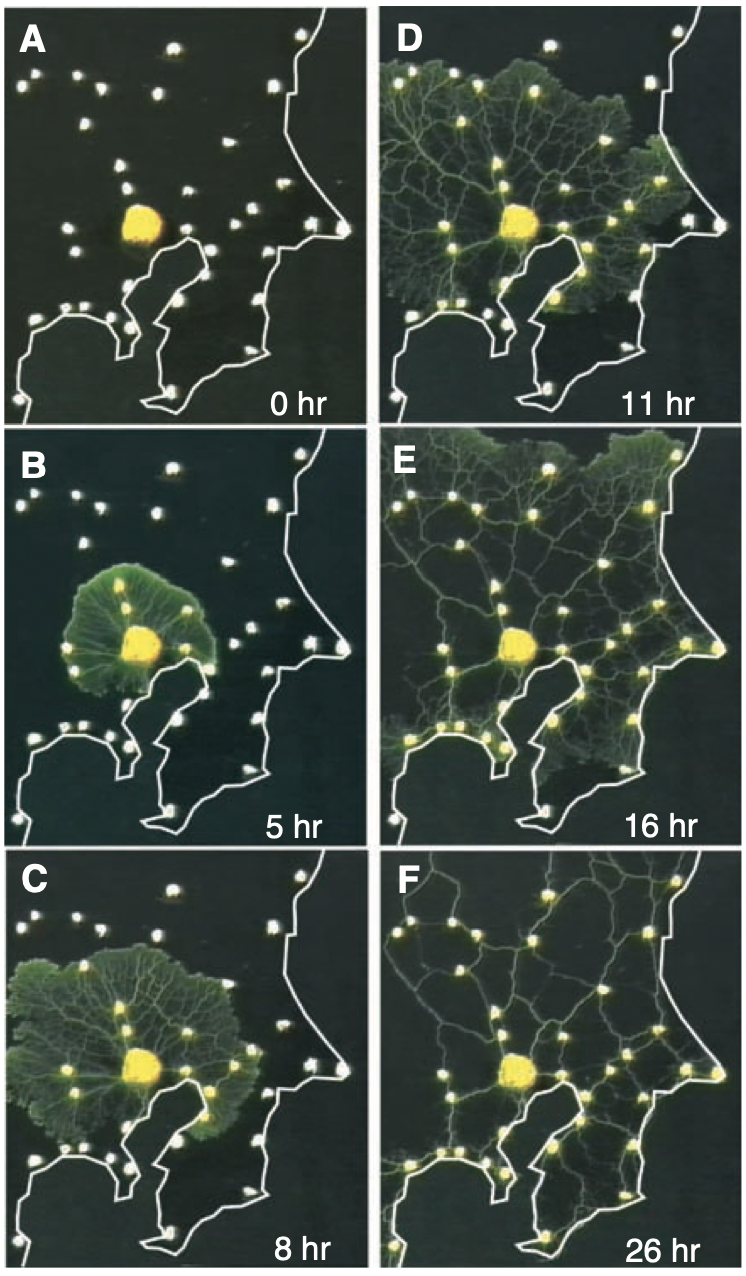

The Physarum Network，图源：Tero A, Takagi S, Saigusa T, et al. Rules for biologically inspired adaptive network design[J]. Science, 2010, 327(5964): 439-442.2020年，几位研究者受到黏菌实验的启发，对宇宙的大尺度结构进行了研究。物理学家认为，从大尺度看，宇宙中的星系、星云等并不是独立飘浮的天体，而是被暗物质气体所构成的细丝连接在一起，构成了宇宙网络。暗物质被认为占宇宙物质总量的85%，但难以直接探测到。于是，研究者借鉴黏菌生长的模型，设计了一种“黏菌算法”，看计算机能否像黏菌那样“爬出”一个宇宙网络。

最终，黏菌算法计算的结果——星系间的暗物质网络与通过最先进的宇宙学方法得出的结果并无二致。不仅黏菌能帮我们理解宇宙，更有科学家直接拿人脑中的神经元网络和宇宙网络作比较。他们发现，尽管二者的尺度和形成过程差异巨大，但人脑神经元网络结构和宇宙的一些宏观特征高度一致。这意味着在系统层面上，二者的演化机制可能具有类似的规律。关于人脑这个我们已知的最复杂的系统与最大的宇宙系统之间的冥冥关联，可以加深我们对这二者本身的研究。从显微镜和望远镜里，我们看到了复杂系统“遥远的相似性”。

复杂科学家不能仅停留在类比的层面，他们有责任找到制约不同复杂系统的普适性规律，甚至为这些规律建立定量化的方程，典型的例子是耗散结构论和广义克莱伯定律。普利高津指出，一个开放的复杂系统要想朝着有序性不断提升的方向进化，就必须让系统保持向环境开放，以确保系统能够从外部环境中获取源源不断的信息源，从而抵消系统内部的熵增。只有当系统从环境中获得的有序（熵减）大于系统内部由于代谢作用而产生的无序（熵增）时，系统整体才有可能逐渐向有序的方向演化。无论是生物系统还是经济社会，负熵流的持续获取都是让复杂系统维持生存的必要性条件。这是一条通用规律，也即著名的耗散结构论的重要推论。

耗散结构论可以说是对热力学第二定律（熵增定律）的拓展和重新表述，并使热力学第二定律被推广到生物体、生态系统、公司组织、城市国家等各种复杂系统中。在中国，一个有趣的现象是，耗散结构论成为很多企业家的口头禅，“避免耗散”“组织的熵”“对抗熵增”之类的说法非常流行。尽管多数时候这类用法不够严格和定量化，例如未说明用什么指标及怎样度量社会系统的熵，但这一现象也体现了其理论的普适性和概念的穿透力。《熵减：华为活力之源》，华为大学，中信出版集团, 2019著名的复杂科学家、圣塔菲研究所前任所长杰弗里·韦斯特 （Geoffrey West）发现，诸如生命、城市、公司等很多复杂系统的新陈代谢和系统规模之间都存在着严格的定量关系，这被称为广义克莱伯定律。最早的克莱伯定律源于生物学研究。法国生物化学家马克斯·克莱伯（Max Kleiber）早在1932年就发现，尽管不同生物体的新陈代谢率和体重不尽相同，但是它们遵循着简单的幂律关系，即生物体的新陈代谢率与其体重的3/4次幂成正比，这意味着生物体体重增大一倍，其新陈代谢率增长近3/4倍。也就是说，新陈代谢的增长要比体重更慢，因此越大的生物体需要的代谢率其实相对来说反而更小。后续研究表明，克莱伯定律适用范围极广，小到单细胞内的线粒体，大到大象、鲸鱼这样的巨型动物，其适用的体重尺度范围足足横跨了1020之大，这在整个宇宙中都是极其罕见的。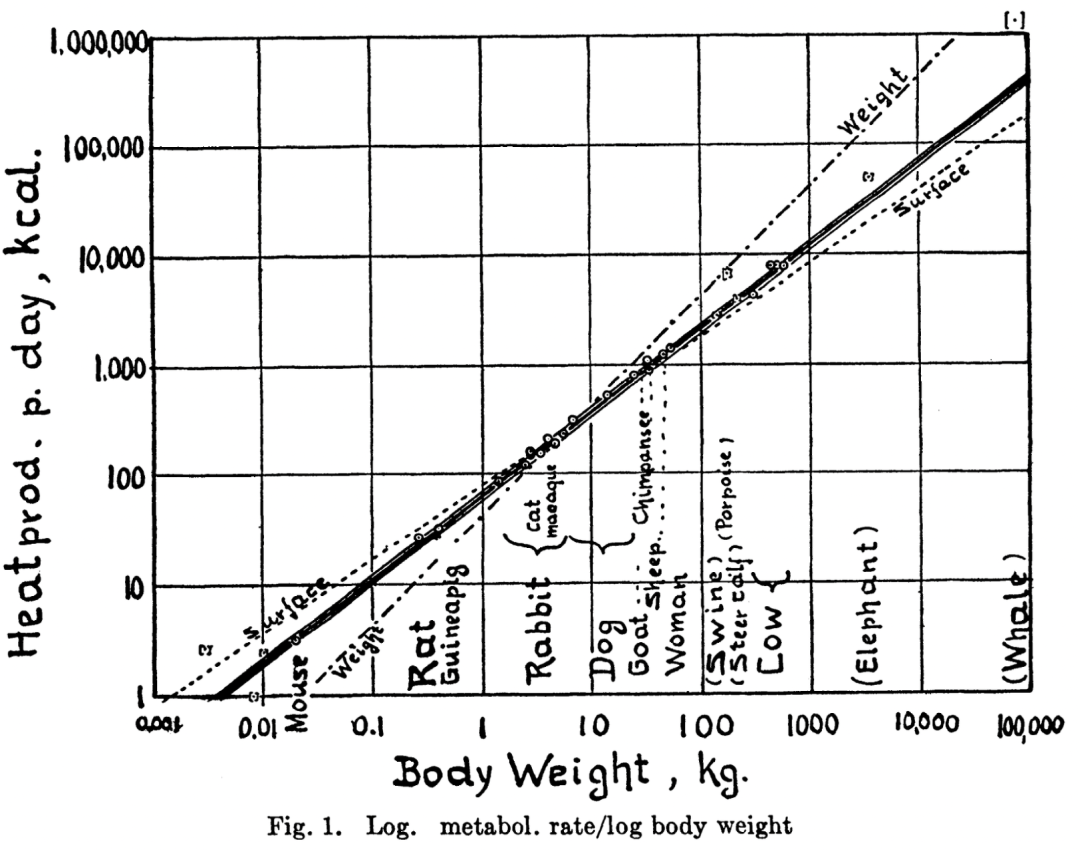体重与代谢率间的幂律关系，图源：Kleiber M. Body size and metabolic rate[J]. Physiological reviews, 1947, 27(4): 511-541.

克莱伯定律意味着生物的新陈代谢率与体重之间并非简单的线性关系，这一点往往挑战着人们，甚至是专业科研人员的习惯性思维。曾经有一种名为LSD的致幻剂被用于动物实验，研究人员发现猫的安全适用剂量大约是0.5毫克，于是推测体重约是猫600倍的大象的安全剂量应该是猫的安全剂量的600倍，即300毫克。在一次实验中，研究人员将297毫克致幻剂注射给大象，但在两个小时内，这头大象接连经历了尖叫、瘫倒、癫痫，最终死亡。这是因理论不足而预测失败的悲剧。事实上，动物能接受多少致幻剂或者吸收多少药物、营养物质，都与其新陈代谢能力有关，而新陈代谢率并不是随着体重线性增长的。根据克莱伯定律，一种体重是猫的600倍的动物，其代谢率仅仅是猫的120倍左右，也就是60毫克。因此，297毫克显然严重超量了。

克莱伯定律甚至可以被推广到企业研究中。笔者就正在和韦斯特等人合作，研究企业中的广义克莱伯定律。如果我们将企业的总资产看作生物体的体重，将企业的净利润看作生物的新陈代谢率，则二者存在着类似克莱伯定律的规律，即存在着可以用幂律函数描述的定量关系，但其幂律指数与生物体的不同，这一规律在多个国家、多种市场、多个不同的历史时期都普遍成立。

城市复杂系统同样遵循着广义克莱伯定律，但与生物和企业都不同的是，城市的新陈代谢与规模之间的幂律指数是一个大于1的数。直观地说，城市人口增加一倍，城市的国内生产总值（GDP）、专利数、人均收入等都要增加超过一倍。这意味着城市越大，其新陈代谢也就越快——大城市有更多的工作机会，也拥有更高的人均GDP和财富，这解释了为什么人们更倾向于挤到大城市。更拥挤的环境承载了更丰富的人际互动、更频繁的信息交换、更复杂的分工协作和更容易被激发与应用的创新想法，但新陈代谢的加快也会让人们的生活更加繁忙，有更多处理不过来的工作邮件和更少的闲暇时光。

根据城市复杂系统的规模理论，城市大小是城市经济发展水平的重要指标。最新研究还表明，城市规模与城市创新能力之间存在一定关系。城市要想具备创新能力，有一定的人口规模门槛。研究者甚至测算出这个门槛是120万人，即超过120万人的城市才可能形成创新经济结构，并实现超线性增长。

早期城市规模研究主要针对美国的城市。美国意义上的“城市”，其范围、聚集性、流动性都与中国不同。近年，针对中国200多座城市超过20年的数据的研究则显示，中国城市与欧美城市的规律相似，仅在指数上略有区别，但都大于1。甚至可以基于城市经济数据等反推真实的城市人口，修正户籍人口等统计数据的偏差。

生物体重、企业资产、城市人口对应的是不同规模大小的复杂系统。如果一个理论模型能够穿透多个不同数量级的复杂系统，那么它就具备了通用性和预测能力。韦斯特把相关研究总结写进了《规模》一书，而对广义克莱伯定律在不同尺度、领域的拓展还在持续进行中。最近有学者通过分析多种灵长类动物的大脑数据，发现大脑的白质占比、大脑内短程连接的丰富性都随着脑容量的大小非线性地变化。人类的脑容量最大，白质占比达到了哺乳类动物中最高的48%。也即人类不仅有更大的大脑，人脑神经元的局部互动密度也更高，这与其脑区的高度分化和高级认知功能的出现密切相关。
《规模》，杰弗里·韦斯特，中信出版集团, 2018

好的理论不能仅仅停留在对已有数据的描述上，还应可以用来预测全新的现象。生物体的克莱伯定律可与生物体内的能量收支方程相结合，推导出一个普遍适用于各种生物体的生长方程，从而精准预测不同物种在不同发育阶段的体重大小，以及解释为什么所有的生物体发展到一定规模大小后就不再生长这一事实。

同样的，从企业的广义克莱伯定律出发，配合上企业的财务平衡方程，我们也能推导出一个企业的生长方程，用来刻画不同市场中代表企业在不同时期的生长行为，甚至预测其发展的天花板。这一逻辑也适用于城市复杂系统。不同的是，由于城市的幂律指数大于1，它的生长方程会呈现出非常复杂的模式。首先，在城市发展规律的制约下，城市人口、GDP、碳排放等指标都会快速增长，在有限的时间内趋近于一个城市无法承载的最高阈值，从而将城市推到崩溃的边缘。这就是我们看到的发生在各个国家的经济危机或战争的原因。为了避免崩溃，城市必须重启生长轨迹，唯一的办法就是通过科技的颠覆式创新重置方程中的各个系数，将城市推入一条新的快速发展轨道。

然而，城市发展在新的轨道之中仍然会遭遇同样的问题，即在有限的时间之内，城市人口、GDP、碳排放等指标可能会再次逼近城市无法承载的极限点，新的危机需要新的科技创新，才能让城市进入一条更新的发展轨道……最终，在更长的时间尺度下，城市的发展曲线呈现出波动性的特点。在科技界，这是人们熟知的S型阶跃式发展轨迹。每一次阶跃都是一次全新的重大技术革命，从早期的互联网革命，到大数据、人工智能革命，不同的科技革命推动了一个全新的S型发展曲线，而不同科技革命之间的间隔却变得越来越短。用韦斯特的话说，人们不仅要不停地在跑步机上奔跑才能赶上社会发展的步伐，还要经常性地跳跃到一架更快的跑步机上。

这必然会将人类的发展轨迹逼近一个无法回避的“奇点”。“奇点”一词最早出现在数学和物理学中，用来表示那些无法定义和描述的奇异时空点。在科技领域，人们用“技术奇点”来形容人工智能的能力超越人类能力的特殊时间点。基于复杂科学的城市发展理论却预测，如果存在这样的技术奇点，那必然是超人工智能出现和环境崩溃同时发生的奇异时空点。

为什么？一切的根源都在于耗散结构和熵。我们知道，所有的复杂系统要想生存下去，就必须不断地从外界获取资源，以抵抗自身内部不断的熵增，从而让系统演化越来越有秩序。如果说人工智能、区块链、元宇宙等高新技术的发展是人类城市系统的高度秩序性的产物，那么它们的代价就是被城市复杂系统排放到外界的各种污染物和温室气体。而且，秩序的产生和废弃物的产生并非完全对称平衡。事实上，由于热力学第二定律的普遍存在，为了获得一点点秩序，我们需要排放更多的废弃物。城市就好比一台大空调，它不停地在城市内部制造着冷气（更多的秩序），代价却是不得不往外部环境中排放大量的废热（更多的污染物和温室气体）。正如空调的运行会让房间和外部环境中的整体热量增加一样，城市这个大空调也正在以更高的速度创造着熵，这些熵以各种不同的现象和形式表现出来。这便解释了本文开篇提到的若干重大问题和重大事件，事实上，它们都是整个人类社会奔向奇点的必然结果。

人类社会正在以更快的步伐奔向奇点。奇点的到来表现为两个方面：一方面是以人工智能为代表的技术的快速发展和社会财富的超高速创造，另一方面则是更加快速的熵的产生和对环境更深层次的迫害。这二者几乎是同步的。尽管人类每次遭遇的危机都是通过科技的颠覆式创新活动加以解决的，但这一次却遭遇到了更大的麻烦，因为更高速度的熵恰恰是科技活动本身带来的，它们仿佛是一枚硬币的两面。那么，人类的解决之道在何方呢？

我们不妨再次利用复杂科学的类比思维，从生物进化史上寻求解决方案。站在进化的长河之上回望，每一次重大的进化事件仿佛都伴随着奇点的产生和复杂性在更高的系统层面以更短的发展周期进行迭代。例如，对单细胞生物体来说，多细胞生物的出现就仿佛是单细胞世界的奇点临近。但奇点的出现并没有让所有的单细胞生物体死亡，而是让它们重新集结，形成了复杂性更高的新的层级——多细胞生物。这种更高层级的个体一旦出现，进化的力量便在多细胞的层面展开，而仿佛与单细胞生物体无关了。

那么，当技术奇点临近，我们人类的进化是不是也会让位于人工智能的进化，或者人类与机器的某种新层面的共生体——全球脑的进化呢？未来复杂科学的进一步发展或许可以给出答案。

参考资料

[1] TERO A, TAKAGI S, SAIGUSA T, et al. Rules for Biologically Inspired AdaptiveNetwork Design[J]. Science, 2010, 327(5964): 439-442.
[2] VAZZA F, FELETTI A. The Quantitative Comparison between the NeuronalNetwork and the Cosmic Web[J]. Frontiers in Physics, 2020, 8: 525731.
[3] BURCHETT J N, ELEK O, TEJOS N, et al. Revealing the Dark Threads of theCosmic Web[J]. The Astrophysical Journal Letters, 2020, 891(2): L35.
[4] ZHANG J, KEMPES C P, HAMILTON M J, et al. Scaling Laws and a General Theoryfor the Growth of Companies[J]. arXiv preprint arXiv: 2109. 10379, 2021.
[5] HONG I, FRANK M R, RAHWAN I, et al. The Universal Pathway to Innovative UrbanEconomies[J]. Science Advances, 2020, 6(34): eaba4934.
[6] ZÜND D, BETTENCOURT L M A. Growth and Development in Prefecture-LevelCities in China[J]. PloS one, 2019, 14(9): e0221017.

本文经授权转载自微信公众号“信睿周报”，原载于《信睿周报》第83期。