纪念法国物理学家查尔斯·卡格尼亚德·德拉图发现临界现象两百周年。

撰文 | 刘一涵、张一、苏桂锋（上海师范大学数理学院物理系）

“几年前，卡格尼亚德·德拉图做了一个实验，使我有机会欲赋新词……我该如何根据连续性定律为液体和蒸汽在此合二为一的这一点命名呢？卡格尼亚德·德拉图没有给它起名字；我该怎么称呼它呢？”——法拉第致胡威立 [1]

一

什么是临界现象？

何谓临界现象（critical phenomena）？其实相变与临界现象是一回事，分开称谓，不过是一个物理学史上的“误会”，以为二者是不同的物理现象。为了具象地表述相变和临界现象，我们以生活中习以为常的水为例，作一个简要直观的说明。

所谓相变，援引大部分教科书的说法，就是物质——例如水——从一种（聚集）形式到另一种（聚集）形式的变化[注1]。人类知道水存在气、液、固三相可以追溯到约4000年前中国和古埃及的历史记录，但要说对相变真正有所认识，却还是最近半个多世纪的事。已故著名统计物理学家卡丹诺夫[注2]（Leo Kadanoff，1937-2015）曾以漂浮在大海中的冰山为例形象地说明水的不同相共存：“大海是液态的水，它包围着冰——即固相的水。微风吹拂着云彩，空气中的水汽同时与固相和液相的水接触。”（当然，严格来说，海水并非只有水这一种化学组分。这段话的原文参见图1的文字说明。）[2]

要研究某种物质的相变，一个基本任务是测定其“相图”，即找出在给定的热力学参量——对于“简单”热力学系统通常是温度T、压强P和体积V下——该物质处于什么相，并确定不同相之间的边界。例如，图2显示了压强-温度（P-T）平面内水的相图，其中明确了水在不同温度和压强条件下的固（浅蓝色区域）、液（蓝色区域）、以及气（赭色区域）三相，以及任意两相之间的边界。接近图2中间的黄点称为三相点（Triple point），顾名思义,是上述三相的交汇点。从三相点出发，沿着气液分界线“上行”，它并不是无限延伸的，而是停止在图2中的红点位置，此即临界点（Critical point）。

对于水而言，临界点处对应的热力学参量的数值是：临界压强Pc = 22.09 MPa；临界温度Tc = 374.14 °C (647.3 K)；临界（比）体积vc = 0.003155 m³/kg。所谓“临界点”，是指超过该点之后，水的气态和液态的差别不复存在，询问水此时是气态还是液态不再有意义。因此，以临界点为界，其上方的区域（参见图2右上角）内为超临界流体（Supercritical fluid），在那个区域，水还会表现出更多新的特点。

图1 L. Kadanoff:“Iceberg floating in the sea. This picture is intended to illustrate different phases of water. The sea is liquid water, which is then in contact with solid water in the form of ice. In the air above, breezes blow clouds through the air, which contains water vapor in contact with both the solid and the liquid forms of water. The change from one form to the next is termed a phase transition.[2]

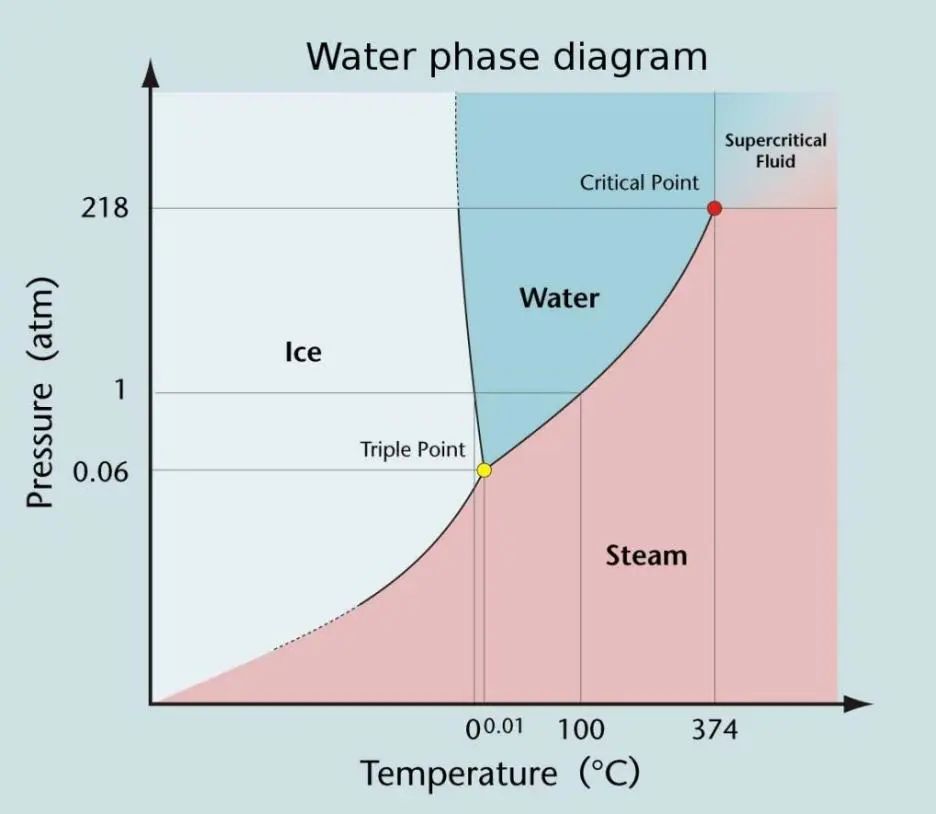图2 水的压强-温度（P-T）平面相图示意 [图片来自网络]

虽然临界点在压强—温度相图上只是一个点，但是临界点附近发生的物理现象却十分丰富——统称为“临界现象”。一个典型的例子就是所谓的“临界乳光”（critical opalescence）：原来透明的气体或液体，当其热力学参量在接近临界点时，它就变得浑浊起来，并逐渐呈现一片乳白色的现象。由统计物理知道，这是由于临界点附近的涨落很大，对光的散射极其强烈而导致的。这可以通过激光穿过处于临界点的相分离散射而观察到，如下的视频演示了等量的苯胺和环己烷混合物的临界乳光现象。

在视频中可见，当达到临界温度，混合物从单相变成两相（相分离）时，屏幕上的光斑就会因此被扰乱。光斑“闪烁”不停直至完全扩散。一旦相变完成，两种物质完全分离，它最终会再次形成单一光斑。当混合物被加热时，同样但反向的模式也可以被观察到。

此外，系统在临界点附近还有其他一些特有的物理现象，如体系的比热在趋近临界点的过程中不断增加，在临界点处比热系数与压缩率趋于“发散”（无穷大）等等。

也许可以说，临界现象的发现始于好奇心。历史上，法国物理学家查尔斯·卡格尼亚德·德拉图（Charles Cagniard de la Tour，1777-1859）于1822年首先在实验当中发现了临界现象。很多人也许并未意识到，今天距离他的发现已经过去了整整两百年！两百年间，物理学发生了翻天覆地的变化。而对临界现象的研究已经发展成为现代凝聚态物理学和复杂系统物理学的一个成熟领域，并且还在不断带来新的惊喜。

我们在本文中将临界现象的发现的历史背景做一浮光掠影的回顾。按照著名统计物理学家杜姆（Cyril Domb，1920-2012）的划分，这一段历史可以归入临界现象研究的“古典时期”[4]。我们也将简略介绍德拉图去世之后，临界现象研究在古典时期的一些重要进展[注3]。

二

德拉图的生平简介

最早发现临界现象的查尔斯·卡格尼亚德·德拉图，1777年3月31日出生于法国巴黎，学生时期就读于巴黎综合理工学院（l’Ecole Polytechnique）及工程地质学院（Écoledu Génie Géographe），此后担任国务委员会的审计员，巴黎城市特别项目主任等公职。同时他又是一名多产的科学家和发明家。除去发现临界现象，从力学到声学，再到化学生物学，他在许多不同领域做出了重要贡献。

德拉图的学术研究始于力学和热力学领域。1809年他发明了新式热机。在1809年到1815年间，他陆续发明了新式液压发动机、新式气泵、以及热驱动绞车等诸多设备。1819年之前，德拉图一直在改进这些发明的设计。此后德拉图对鸟类飞行和人类发声的物理学产生了浓厚兴趣，开始研究声学和声音的产生机理，并在这个领域投入了大量精力。值得注意，正是这一偶然地兴趣转向，导致了日后他发现了临界现象。在1828年到1831年间，德拉图开始研究结晶过程和酸对碳的影响，以及磷、硅及其结晶，甚至砂浆（mortar）的硬化。在1832年至1835年间，德拉图又对阿基米德螺杆（Archimedean screw）原理在气泵上的应用发生了兴趣[5]。

1835年德拉图开始转向酒精发酵的研究。这一工作在1836年到1838年间达到巅峰——1836年底，他发现啤酒酵母中含有一种活性物质。德国生理学家施万[注4]（Theodor Schwann，1810-1882）也几乎同时独立地得出了同样的结论，但是化学家李比希[注5]（Justus von Liebig，1803-1873）的批评使得这一观点被推迟了足足20年，直到1857年，法国生物学家巴斯德（Louis Pasteur，1822—1895）才再次宣布了这一发现。

顺便提及，目前关于德拉图的可靠照片或肖像尚存争议。在某些文献以及互联网流传的一些照片或画像往往相互矛盾。例如，互联网常见的如图3所示，据称是德拉图的肖像，有比较可靠的证据表明其实是英国王子查尔斯·爱德华（Charles Edward）[注6]。

图3 互联网上流传的一些所谓德拉图的肖像并不可靠

三

临界现象的发现与早期历史

17世纪末和18世纪初蒸汽机的发明激发了人们对高温高压下流体行为的兴趣。法国物理学家帕潘（Denis Papin，1647-1712）在英国皇家学会做玻义耳（Robert Boyle，1627-1691）助手期间，发明了蒸汽机的前身——“帕潘蒸锅”（Papin’s digester，参见图4的示意图和模型）。

他还特别注意到，当在高压下加热，水保持在液相的温度远高于通常的沸点，也就是沸点的温度随着压强的增加而增加。到了18世纪下半叶，法国化学家拉瓦锡（Antoine-Laurent de Lavoisier，1743-1794）证明了气体和蒸汽其实是一回事，是固体和液体之外的物质的第三种状态。

他还提出，气体可以在足够低的温度和足够高的压强下液化。这个认识导致1784年克鲁埃（Jean-Francois Clouet，1751—1801)[注7]和蒙日（Gaspard Monge，1746-1818）[注8]通过冷却和压缩实现了气态二氧化硫的液化，这是首次成功的气体液化。随后英国物理学家法拉第（Michael Faraday，1791—1867）通过一系列成功的实验将气体液化[7, 8]。氢、氧、氮和一氧化碳，这些以前被认为不可冷凝的气体——一度被称为“永久气体”（permanent gases）——最终都在1877年实现了液化。

图4 帕番热压蒸锅（Papin’s digester）的示意图和模型 图片来源：来自网络

德拉图就是在帕潘热压蒸锅的有关实验中发现临界点的存在的。1822年，本来出于对声学的兴趣，德拉图将燧石（flint）球放在部分填充了液体的蒸锅中加热。在转动实验装置时，固体的燧石球因为穿过气液两相的界面而产生了水的拍溅声。德拉图注意到，当实验中温度远远超过液体沸点时，水的拍溅声在超过特定温度后就停止了。这实际上意味着前文提及的超临界流体相的发现（图2当中红色临界点的上方区域）。在这个相中由于不存在气液相边界，因此也不存在表面张力。超临界流体也可以像液体一样溶解物质，也可以像气体一样在固体中扩散。目前对于超临界流体的研究仍然是一个重要的方向。

在发表于《化学和物理年鉴》（Annales de Chimie et de Physique）[9]的两篇论文中，德拉图描述了他如何在高压下加热密封的酒精玻璃管（参见图5德拉图的论文首页）。他观察到液体膨胀到大约原来体积的两倍，然后变成了透明的蒸汽，管子看起来像是空的一样。但是当重新冷却时，玻璃管内出现了一团“云”。现在我们已经认识到，这其实就是临界点处临界乳光现象的表现。为了使读者有一个直观的印象，图6显示了乙烷的临界乳光。德拉图还注意到，当超过特定温度时，增加压强并不能阻止液体的蒸发。

图5 德拉图的论文[9]的首页，他在论文中报告了临界现象的发现

图6 乙烷的临界乳光现象（中图黄圈内） 图片来源：https://handwiki.org  

在随后的另一篇论文[10]中，德拉图想要证明特定的极限温度的存在是一种普遍现象。所谓极限温度，是指在此温度之上，无论压强如何，液体都会蒸发。德拉图在论文中报告了几种物质实验的结果。他通过表面张力为零时液体弯月液面消失为标志，来确定对应的临界温度。德拉图测量了水、酒精、乙醚和二硫化碳的临界温度Tc，发现对应每种物质都确实有一个特定的温度，在该处即使不增加压强液体也会蒸发，而超过这个温度，液体全部蒸发。德拉图测得水的临界温度约为362℃。考虑到当时的历史条件，这已经是一个颇为准确的结果（现代测量的结果约为374℃）。他在论文中称，这种“特定的状态”（état particulier）：“总是需要非常高的温度，几乎与管道的容量无关” [10]。我们现在知道，这种“特定的状态”标志着相平衡曲线的终点，即临界点。

许多德拉图的同时代人并未意识到他的发现的重要意义，认为这一结果仅对德拉图实验所用的物质才成立，而非普遍现象[11]。但是法拉第显示出他深刻的物理洞察，他认识到了德拉图的工作的价值[12]。1844年，法拉第在给胡威立（William Whewell，1794-1866）[注9]的信中写道：“几年前，卡格尼亚德·德拉图完成了一个实验，它给了我一个发明新词的机会。”接着，法拉第谈到现代意义下的临界点，“根据连续性定律（law of continuity），我该如何给液体和蒸汽合二为一的点命名呢？卡格尼亚德·德拉图没有命名它，那么我该如何称呼它呢？”（参见前注11）胡威立建议称其为汽化点，或者液体的非液化点，或者德拉图态也可以，法拉第在其后来的论文中用了“卡格尼亚德·德拉图态”（Cagniard de la Tour’s state）和“卡格尼亚德·德拉图点”（Cagniard de la Tour point）[13]。1859年7月5日，德拉图在巴黎去世。然而，他的实验发现开启了临界现象研究的古典时期，以及其后的智力探险之旅。

我们今天使用的“临界点”（critical point）一词是由英国物理化学家安德鲁斯[注10]（Thomas Andrews，1813-1885）在1869年——德拉图去世十年后——提出的，他于同年发现了“超临界流体”，并将他的研究成果以《论物质气态与液态的连续性》（on the continuity of the gaseous and liquid states of matter）为题发表在当年的《哲学杂志》上[14]（参见图7）。在这篇著名论文中，安德鲁斯研究了二氧化碳液气两相共存线的压强—体积曲线，进一步阐明了德拉图所谓的“特定状态”——即只有在一定的温度和压强下——气体才可能凝结成液体，或者液体才可能蒸发成气体。这一点之上是超临界相，在那里液体和蒸汽之间的区别消失了（参见图8）。

1873年，荷兰物理学家范德瓦尔斯（J. H. van der Waals，1837-1923）首次从理论上清晰地解释了物质气相和液相之间的连续性。范德瓦尔斯在其博士论文中表明[15]，可以引入分子间相互作用推广理想气体定律，并得到了以他名字命名的范德瓦尔斯气的物态方程，定性解释了安德鲁斯的实验结果。当时著名的物理学家麦克斯韦和玻尔兹曼都对范德瓦尔斯的结果给予高度评价[4]。范德瓦尔斯的工作反过来又启发了他的同胞，荷兰物理学家昂内斯（Heike Kamerlingh Onnes，1853-1926）。后者可以据此估计永久气体的临界点，这为氦最终在低温下——约4K左右——液化提供了理论基础。随后低温的获得又导致超导现象的发现。但是关于低温的探索历史，则又是另一个故事了[16]。

物质在临界点附近的行为可以通过一系列临界指数来刻划。从范德瓦尔斯物态方程中得到的“临界指数”，实际上是简单的平均场（Mean Field）数值，它们并不符合实际测量出来的热力学系统的临界指数值。比利时物理学家沃沙费尔特（Jules-Emilé Verschaffelt， 1870-1955）[注11]在1896年首先通过实验发现了这一点[17]。他重新测量了二氧化碳在毛细管中的上升量，并结合新的共存密度实验值对共存曲线数据进行了分析，发现同平均场值并不吻合。然而沃沙费尔特的实验结果并未引起当时物理学家的重视。20世纪30年代，前苏联著名物理学家朗道（Lev Davidovich Landau，1908-1968）继续发展了进行系统化平均场处理相变的普遍框架，即朗道连续相变理论，这是相变唯象理论的一座高峰[18]。

图7 1869年安德鲁斯发表的《论物质气态与液态的连续性》论文首页，开门见山提及德拉图关于临界现象的实验发现 [14]

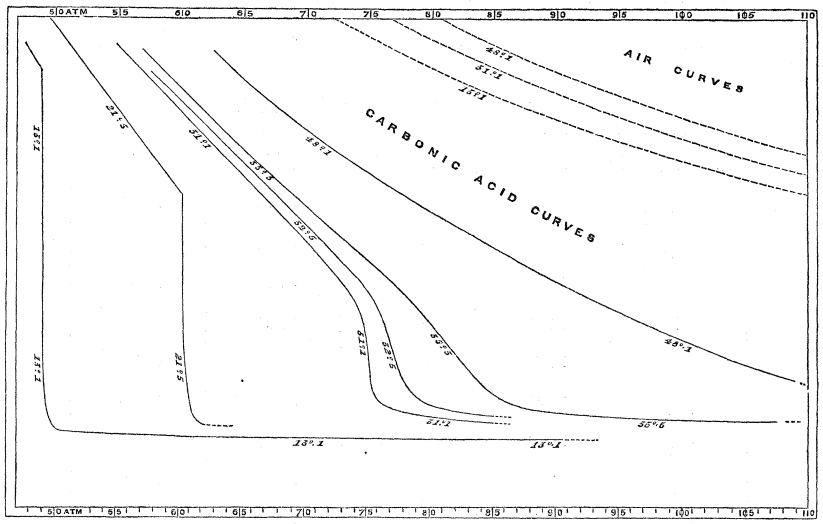
图8 1869年安德鲁斯的《论物质气态与液态的连续性》论文内图[14]。图中坐标横轴为压强，纵轴为体积。可以看到随着温度提高，共存的气液两相的密度差逐步趋于零直至消失。

图9 读者朋友，你能从这张著名的合影中找到沃沙费尔特吗？（答案见文后注释[12]）图片来源：网络

在另一关于磁性的研究路线上，法国物理学家居里（Pierre Curie，1859-1906） 发现铁磁材料在超过临界温度时会出现退磁现象[19]，这一临界温度通常被称为“居里点”（Curie point）。1895年他注意到气液相变和铁磁相变之间的相似性，提出了临界现象的“普适性”（universality）的重要概念[注13]。为了理解磁性起源，1920年德国物理学家楞次（Wilhelm Lenz，1888-1957）引入了一个简单模型——现在通常称为“伊辛（Ising）模型” [20]。

1924年，楞次的学生伊辛（Ernst Ising，1900-1998）在他的博士论文中解决了该模型一维的情况，发现不存在相变，但是他错误地将这一结论推广到二维情形，认为二维伊辛模型也不存在相变[21]。中间经过派尔斯（Peiers）[22]和克拉默斯及瓦尼尔（Kramers & Wannier）[23]等人的工作，最终昂萨格（Lars Onsager，1903-1976）在1944年解析地计算了在没有外磁场的情况下二维伊辛模型的比热[24]——昂萨格的这一工作如此重要，以至于杜姆称其为“昂萨格革命”（Onsager Revolution）[4]。

昂萨格还在1949年给出了未予证明的自发磁化公式[25, 26][注14]，该公式是杨振宁（1922-）在1952年予以证明的[27]。然而三维伊辛模型的精确解迄今为止仍然没有被求解出来，这对物理学家始终是一个巨大的挑战。伊辛模型本身的历史足以构成一本专著的内容，我们不再赘述，仅在表I中列举一些重要的进展，感兴趣的读者可以进一步阅读有关文章[36]，以及文内所引文献。表I Ising模型精确解的历史进程

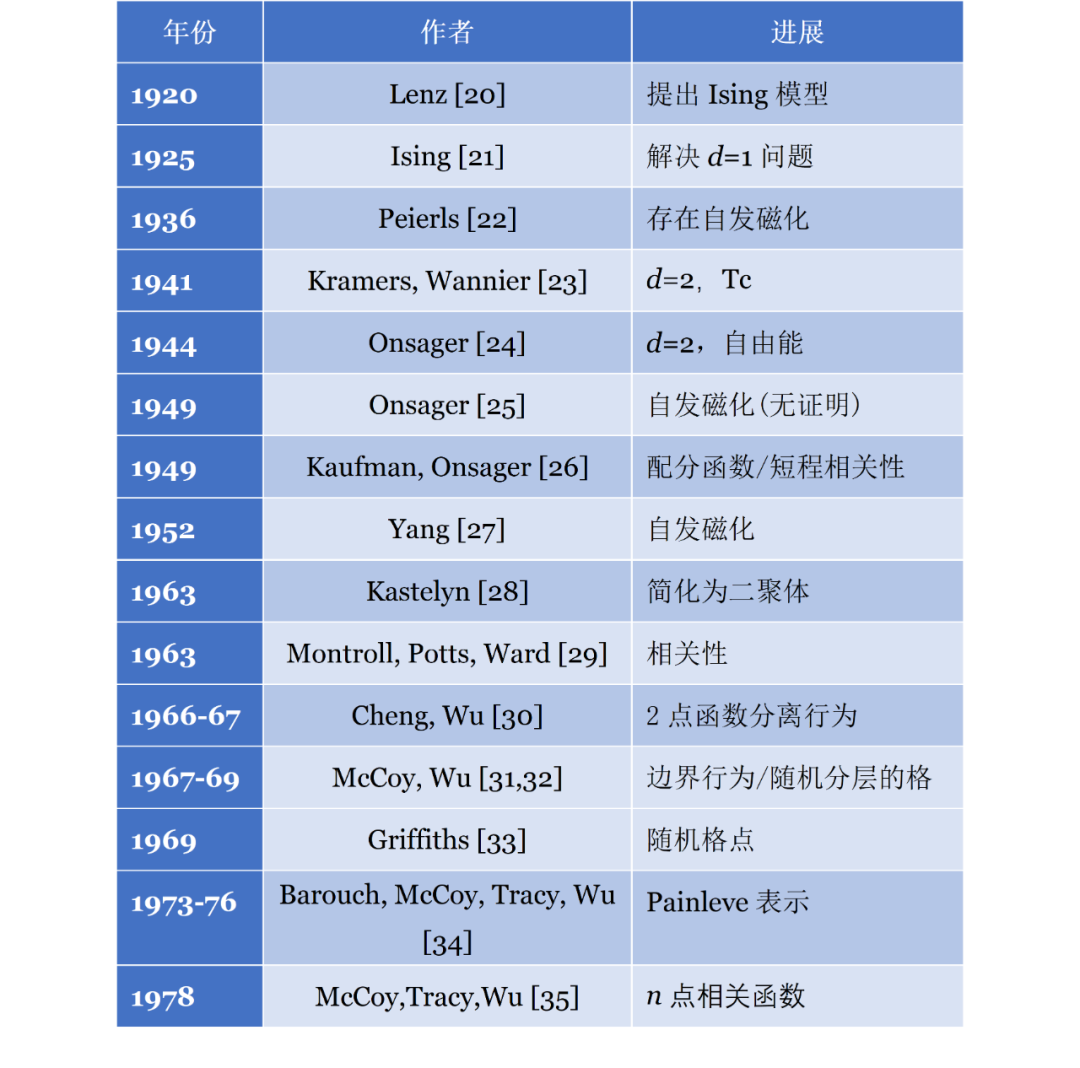
在缺乏三维伊辛模型精确解的背景下，人们不得不依赖于数值模拟。杜姆在其1949年的博士论文中提出了高、低温展开方法（参见[4]中引述）。而今天被广泛使用的则是迈绰泡利斯[注15]（Nicholas Metropolis，1915-1999）和乌拉姆[注16]（Stanislaw Ulam，1909-1986）在1949年提出的蒙特卡罗（Monte Carlo）方法[37]。

20世纪60年代，卡丹诺夫和费舍尔[注17]（Michael Fisher，1931-2021）意识到相变的一般理论框架必须基于“标度假设”（scaling hypothesis），特别是从标度假设引出了描述接近临界点的各种临界指数之间的“标度关系”（scaling relations）。这一思想通过威尔逊[注18]（Kenneth G. Wilson，1936-2013）于1971年提出的“重整化群”（renormalization group）方法[38]，为临界现象完整的理论描述开辟了道路。

至此，我们对临界现象的研究和认识达到了一个新的高度，同时又是一个新的起点。
 

注释

[1] 限于篇幅，我们在此不进一步讨论相变的分类。对（连续）相变的现代解读还包括所谓对称性破缺（symmetry breaking）。对相变与临界现象发展历程的全貌感兴趣的读者，请参阅引人入胜的科普读物佳构，《边缘奇迹: 相变和临界现象》，于渌，郝柏林，陈晓松著，科学出版社（2005）。 

[2] 卡丹诺夫（Leo Kadanoff）美国著名统计物理学家，曾任美国物理学会（APS）主席，在统计物理、混沌理论、凝聚态物理等领域贡献卓著。 [3] 由于本文着重介绍卡格尼亚德发现临界现象，因此笔者对其后古典时期的研究并未详细展开讨论，难免会有遗漏，期待以后有机会另文撰述。 [4] 施万（Theodor Schwann），德国生理学家，细胞学说的创立者之一，酵母菌有机属性的发现者，胃蛋白酶的发现和研究者，创造了“新陈代谢（metabolism）”一词。 [5] 李比希（Justus von Liebig），德国化学家，被认为是有机化学的奠基人之一。 [6] 它实际上是1745年左右一位名叫M. Q. de La Tour的画家创作的油画，在爱丁堡的苏格兰国家肖像画廊展出，参见https://www.britannica.com/topic/Jacobite-British-history。 [7] 克鲁埃（Jean-Francois Clouet），法国化学家、冶金学家，推动了法国化学研究向具体问题的转变，促进了冶金工业的发展。 [8] 蒙日（Gaspard Monge），法国数学家、物理学家。创立了画法几何学、偏微分方程的特征理论，推动了空间解析几何学、微分几何学、纯粹几何学的发展。 [9] 一般译为胡威立（William Whewell），19世纪英国博学多才的学者，也是当时英国学界最有影响力的人物之一。他在力学、矿物学、地质学、天文学、政治经济学、建筑学等诸多学科上著书立说，在科学哲学、科学史和道德哲学领域留下许多著作，如《归纳科学史》（3卷本，1837）、《归纳科学原理》（1840）、《科学思想史》（2卷本，1858）、《发现的原理》（1860）等。他是英国科学促进会的创始成员之一和主席，皇家学会会员，地质学会会长，剑桥大学三一学院的长期院长。他的影响得到了同时代的约翰·赫歇尔、查尔斯·达尔文、查尔斯·莱尔和迈克尔·法拉第等当时主要科学家的认可，他们经常向胡威立寻求哲学和科学建议，甚至是寻求学术术语方面的帮助。胡威立发明了法拉第的术语“阳极”（anode）、“阴极”（cathode）和“离子”（ion）。一段有趣的历史是，1833年，为了回应诗人S.T.柯勒律治的挑战，胡威立发明了单词“scientist”，此前使用的术语只有“自然哲学家”（ natural philosopher）和“科学从业者”（man of science）。 [10] 安德鲁斯（Thomas Andrews），英国物理化学家，伦敦皇家学会会员、爱丁堡皇家学会会员，曾任贝尔法斯特女王学院副院长、化学教授。主要从事物质临界状态的研究。 [11] 沃沙费尔特（Jules-Emilé Verschaffelt），比利时物理学家，师从荷兰物理学家、低温物理学奠基人昂内斯（Heike Kamerlingh Onnes）。 [12] 后排左起第七人（薛定谔和泡利之间）：Auguste Piccard, Emile Henriot, Paul Ehrenfest, Edouard Herzen, Theophile de Donder, Erwin Schrodinger, J.-E. Verschaffelt, Wolfgang Pauli, Werner Heisenberg, Ralph Fowler; Leon Brillouin.[13] 在笔者(张一)看来，居里在1894年提出的居里原理（Curie’s Principle）指出了对称性在物理学中的重要地位。关于这一原理虽然尚存争议，但是其历史作用长期以来似乎被忽视了。 [14] 1948年8月23日，L. Tisza在康奈尔大学做关于伊辛模型的演讲。演讲结束时，Onsager走到黑板前宣布他和Bruria Kaufman已经解决了这个问题，并把公式写在了黑板上。1949年，Onsager在意大利佛罗伦萨的统计力学会议上重申了他的结果。然而，Kaufman和Onsager从未正式发表过他们的计算。 [15] 迈绰泡利斯（Nicholas Metropolis），希腊裔美国物理学家。在蒙特卡洛方法的研究方面具有重要贡献。 [16] 乌拉姆（Stanislaw Ulam），美国数学家、核物理学家。发明了氢弹设计的泰勒-乌拉姆构型，在数论、集合论等方面亦有贡献。 [17] 费舍尔（Michael Fisher），英国统计物理学家，英国皇家学会、美国物理学会（APS）成员，在相变和临界现象方面做出重要贡献。 [18] 威尔逊（Kenneth Wilson），美国理论物理学家，因建立重正化群变换理论荣获1982年度诺贝尔物理学奖。 

参考文献

[1] 原文如下：M. Faraday to W. Whewell：“Cagniard de la Tour made an experiment some years ago which gave me occasion to want a new word [……] how am I to name this point at which the fluid and its vapour become one according to a law of continuity. Cagniard de la Tour has not named it; what shall I call it?”。Letter dated November 12, 1844, published in L. P. Williams, The Selected Correspondence of Michael Faraday (Cambridge: Cambridge Univ. Press, 1971), Vol. 1, 427-428.[2] L. P. Kadanoff, arXiv: 0906.0653v2[3] 参见：https://www.doitpoms.ac.uk/tlplib/solid-solutions/demo.php[4] C. Domb, The critical point: a historical introduction to the modern theory of critical phenomena, Taylor & Francis (London 1996).[5] B. Berche, M. Henkel, and R. Kenna, J. Phys. Studies 13 (2009) 3201.[6] A.-L. Lavoisier, Recueil des mémoires de chemie (1792) 348; republished in Œuvres de Lavoisier, publiées par les soins de son excellence le ministre de l’instruction publique et des Cultes (Paris: Impr. impériale, 1862), t. II, 783-803.[7] M. Faraday and H. Davy, Phil. Trans. R. Soc. Lond. 113 (1823) 160-165; M. Faraday, ibid., 189-198.[8] M. Faraday, The Quarterly Journal of Science, vol. xvi. (1824), pp. 229-240; reprinted in The Liquefaction of Gases. Papers by Michael Faraday, F.R.S. (1823-1845) with an Appendix consisting of Papers by Thomas Northmore in the Compression of Gases (1805-1806), Alembic Club Reprint No.12, pages 19-33, Pub. by William F. Clay, Edinburgh and Simpkin, Marshall, Hamilton, Kent & Co., London (1896).[9] C. Cagniard de la Tour, Ann. Chim. Phys., 21 (1822) 127-132; Supplément, ibid., 178-182.[10]原文如下：“... cet état particulier exige toujours une température très-élevée, presque indépendante de la capacité du tube”。C. Cagniard de la Tour, Ann. Chim. Phys., 22 (1823) 410-415.[11] Y. Goudaroulis, Revue d’Histoire des Sciences 47 (1994) 353-379.[12] M. Faraday, letter to W. Whewell, 9th November 1844. 也参见[11]。[13] M. Faraday, Philosophical Transactions for 1845, Vol. 135, pp 155-177.[14] T. Andrews, Phil. Trans. Roy. Soc. London 159 (1869) 575-590.[15] J. D. van der Waals, doctoral thesis, Leiden (1873); reprinted in On the continuity of gaseous and liquid states, ed. with an introductory essay by J. S. Rowlinson, North-Holland Amsterdam (1988).[16] 可参见，R. Srinivasan, Resonance, Vol. 1, No.12 (1996) p. 6.[17] J. E. Verschaffelt, Verslagen 5 (1896) 94-103.[18] L. D. Landau, Nature 137 (1936) 840-841.[19] P. Curie, Archives des Sciences physiques et naturelles, 3e période, tome XXVI (1891) p.13; reprinted in: Oeuvres de Pierre Curie, pp 214-219, Paris: Gauthier-Villars (1908).[20] W. Lenz, Physikalische Zeitschrift. 21 (1920) 613-615.[21] E. Ising, Zeitschrift für Physik 31 (1925) 253–258 (题为Report on the theory of ferromagnetism).[22] R. Peierls, Proc. Cambridge Phil. Soc. 32 (1936) 477-481.[23] H. A. Kramers and G. H. Wannier, Phys. Rev. 60 (1941) 252-262; Part II, ibid., 263-276.[24] L. Onsager, Phys. Rev. 65 (1944) 117-149.[25] L. Onsager, Nuovo Cim 6 (Suppl 2) (1949) 279–287.[26] B. Kaufman, Phys. Rev. 76 (1949) 1232-1243; B. Kaufman and L. Onsager, ibid. (1949) 1244-1252.[27] C. N. Yang, Phys. Rev. 85 (1952) 808-816.[28] P. W. Kastelyn, J. Math. Phys. 4 (1963) 287-293.[29] E. W. Montroll, R. B. Potts, and J. C. Ward, J. Math. Phys. 4 (1963) 308-322.[30] T. T. Wu, Phys. Rev. 149 (1966) 380-401 (Part I); Phys. Rev. 155 (1967) 438 (Part II); H. Cheng and T. T. Wu, Phys. Rev. 164 (1967) 719-735 (Part III).[31] B. M. McCoy and T. T. Wu, , Phys. Rev. 162 (1967) 436-475 (Part IV).[32] B. M. McCoy and T. T. Wu, Phys. Rev. 176 (1968) 631-643; B. M. McCoy, Phys. Rev. Lett. 23 (1969) 383-386; B. M. McCoy, Phys. Rev. 188 (1969) 1014-1031.[33] R. B. Griffiths, Phys. Rev. Lett. 23 (1969) 17-19.[34] E. Barouch, B. M. McCoy and T. T. Wu, Phys. Rev. Lett. 31 (1973) 1409-1411; C. A. Tracy and B. M. McCoy, Phys. Rev. Lett. 31 (1973) 1500-1504; T. T. Wu, B. M. McCoy, C. A. Tracy and E. Barouch, Phys. Rev. B 13 (1976) 315-374.[35] B. M. McCoy, C. A. Tracy and T. T. Wu, Phys. Rev. Lett. 38 (1977) 793-796; B. M. McCoy and T. T. Wu, Phys. Rev. D 18 (1978) 1243-1252; B. M. McCoy and T. T. Wu, Phys. Rev. D 18 (1978) 1253-1258.[36] 关于Ising模型历史的精彩介绍可参见，例如，S. G. Brush, Reviews of Modern Physics 39 (1967) 883-893 (题为History of the Lenz-Ising Model); 以及M. Niss的“三部曲”：M. Niss, , Arch. Hist. Exact Sci. 59 (2005) 267-318 (History of the Lenz-Ising Model 1920-1950); ibid. 63 (2009) 243 (1950-1965); ibid. 65 (2011) 625 (1965-1971).[37] 参见N. Metropolis and S. Ulam, Journal of the American Statistical Association, 44 (1949) 335-341; 亦可参见历史回顾 N. Metropolis, Los Alamos Science 15 (1987) 125.[38] 如今重整化群技术已经被广泛用于各种相变和临界现象的理论研究中，几乎在每一部临界现象的专著中都可以找到有关重整化群的细致的讨论。我们在此推荐它的提出者K. G. Wilson的综述：K. G. Wilson, Rev. Mod. Phys. 55 (1983) 583.

出品：科普中国