我在上一篇《返朴》文章《气象学家与数学家的混沌接力》中讲到，是“混沌之父” 爱德华·洛伦茨揭示出天气变化具有内在“蝴蝶效应”混沌本质的那篇重磅论文《确定性的非周期流》，催生出“李-约克混沌”的数学概念。然而他们据此而写成的文章初稿却差点与《美国数学月刊》（下称“《月刊》”）失之交臂。

李-约克定理被老师提出、学生证明后，文章真的按照李天岩的 “玩笑式建议”投给了《月刊》。为什么这么漂亮的一个数学定理加上一个新定义的数学名词“混沌”要投给一个数学上的“大众杂志”呢？约克自有打算，他深知这个来源于自然科学却反过来又能为自然科学提供广泛服务的数学定理将给科学界传递一个极其重要的信息：确定性的世界中也会隐藏着随机性，所以他想让尽可能多的人了解并领会这个观念。众所周知，越是高深专门的学术期刊，读者人数越是稀少，约克决心要让天下的人都知道他和李天岩关于函数迭代的绝妙想法和惊人结果。《月刊》是全世界读者人数最多的数学期刊，于是约克将希望传播混沌之数学刻画的目光投向了它。

然而，投稿结果却遭遇了滑铁卢，并且之后的故事甚至颇具戏剧性。文章投出去不久就被编辑退回，理由是该文写得过于研究性，不太适合一般读者，尤其是作为主要读者群的大学生。因此编辑建议作者转投研究型专业杂志。或许编辑还是看到了此文数学内容的独具魅力之处，在拒稿信的末尾又加写了一句话：倘若把文章改写到一般学生都能读懂的地步，可以再投回《月刊》考虑。由于这句并非“多余的话”，最后的结局让这份杂志与读者一样也获益甚多：我的韩国裔师兄李弘九教授五年前曾告诉我，李-约克论文在明年将庆祝创刊130周年的《美国数学月刊》历史上被引用次数排名第二高；根据“谷歌学术”上的记录，它已被引用了超过5670次，这对通常而言引用次数远非生命科学和工程技术等应用学科对手的数学文章而言，是极为罕见的。

但是，当时的李天岩实在太忙。他一生中最显赫的三项数学贡献都是在那两三年做出来的，除了这项“周期三”的工作已写出文章外，他还在继续从事微分方程方面的研究，同时又在自己选修的一门研究生课程《非线性方程组数值解》中获得灵感而穿梭于大学的计算中心和公寓之间，埋首于通过数值逼近构造性证明布劳威尔不动点定理，即将开辟出求解非线性方程组的“现代同伦延拓法”这一崭新的疆场。他既没有工夫修改这篇文章，也不知道怎么改它。由于没有新的应用论题的激励，约克教授一时也缺乏动力按编辑的建议行事，于是乎，这篇文章就被他们放在一旁束之高阁了将近一年。

上天终于赐给他们一个修改文章的契机。1974年是马里兰大学数学系“情系”生物数学的“特殊年”。这一年里的每个礼拜都有“生物数学”领域里的优秀学者来这里演讲。在五月份的第一个星期，普林斯顿大学冠名为“1977届”的动物学讲座教授罗伯特·梅被请来演讲一周。在星期五的报告中，梅教授专门讲述了他在种群动力学中迭代那个逻辑斯蒂映射后的种种发现：在繁殖率参数μ由3变到4的过程中，函数迭代点数列之最终性态令人眼花缭乱地愈变愈复杂。他对这一现象深感困惑，难以合理解释，觉得或许是因为计算误差从中作怪。听完梅博士的报告后，约克在送他去往飞机场的途中，把自己和李天岩被冷淡了将近一年的那篇文章递给他看。对方一读到文章中得出的“周期三则乱七八糟”结论后，大为吃惊，马上认定此定理大大解释了他的疑问。（参见《一名生态学家的数学探索》）

约克从梅那里获得了修改文章的动力，他送客归来后立刻跑到李天岩的办公室大叫：“我们应该马上改写这篇文章！”文章在两个星期内以更阐述性的写作方式修改完毕，重新投回《月刊》，三个月后被编辑接受，并最终刊登在第八十二卷第十期上，页码为985-992，仅仅八页长。

《美国数学月刊》1975年12月期

梅幸运地成了李-约克定理的第一个受惠人，所以也理所当然地充当了志愿宣传员的角色。同年夏天他去欧洲讲演时，到处传播李-约克定理，“李-约克混沌”的概念很快四处散开，也让概念的两位提出者声名远播。一篇并非刊登在顶尖数学期刊，而是发表在面向广大读者的阐述性数学杂志上的文章，成了掀起数学界、科学界及工程界对混沌动力系统理论和应用研究新热潮的开路先锋之作。

这位讲俄语的数学家就是沙可夫斯基(Oleksandr Mykolayovych Sharkovsky，1936-2022)，乌克兰基辅人，于1964年在祖国的《乌克兰数学杂志》(Ukrainian Mathematical Journal) 第十六卷中刊登了一篇俄语论文，其标题的中文翻译是“实数轴上到自身的连续映射循环之共存性”。在文章中他历史上第一次对所有的自然数给出了如下的排序，现称为沙可夫斯基序列：

3, 5, 7, 9, 11, 13, 15, 17, … ,  即除1以外的所有奇数;

2ⁿ·3, 2ⁿ·5, 2ⁿ·7, 2ⁿ·9, … ,  n = 1, 2, 3, …,  即2ⁿ乘以第一行的每一个数;

…, 2⁵,  2⁴,  2³,  2²,  2¹,  2⁰，即由大到小排列2 的所有次方。

然后他证明了如下的结果：

沙可夫斯基定理  如果将实数轴映到自身的一个连续函数有周期为m的周期点，则对在沙可夫斯基序列中排在m 后面的任一个自然数n，该函数也有周期为n的周期点。

由于在沙可夫斯基序列中，3是排在首位的自然数，故上述定理的一个特别推论是：如果将实数轴映到自身的一个连续函数有周期为3的周期点，则对任一个自然数n，该函数也有周期为n的周期点。这恰恰是李-约克定理的结论(i)。然而，沙可夫斯基的定理就到此为止了，它没有关于在该函数迭代过程中任何不规则行为的结论，而这个根本性的结论出现在李-约克定理的结论(ii)和(iii)中！

更进一步，真正的李-约克定理并非是几乎所有知道李-约克论文标题或听说过“李-约克混沌故事”却没有读过原始论文的人们或许以为的“若周期三点存在，则结论如何如何”的那个形式，而是其假设条件更广、应用价值更大的一颗数学蓝宝石。在李天岩与约克的论文《周期三则意味着混沌》中，定理的假设远比“存在周期三点”更为宽阔：存在一个点a，使得该点被给定连续函数持续迭代两次后都变大，但在第三次迭代后却跌落到小于或等于a，或a在该函数接连迭代两次后都变小，但在第三次迭代后却跳升到大于或等于a。如用代数不等式表示，就是

f³(a)  ≤  a  <  f(a)  <  f²(a)      或      f³(a)  ≥  a  >  f(a)  >  f²(a)。

而“周期三点存在”这一假设只是满足如上条件的一个特例而已，亦即上面的广义不等号“≤”或“≥”换成等号“=”。这个特殊的情形成就了文章的四个英文单词精炼标题，但却导致了一个小小的副作用，就是让许许多多没有读过文章主体的人误认为定理只对具有周期三点的连续函数成立。

于是，最准确的李-约克混沌定理是如下的命题表述：

李-约克定理     设f是一个连续函数，将定义域区间映到自身。若在定义域中存在一点a使得

f³(a)  ≤  a  <  f(a)  <  f²(a)      或      f³(a)  ≥  a  >  f(a)  >  f²(a)，

则

(ii)对任一自然数n，f有一个周期为n的周期点。

(ii)存在定义域的一个不可数的子集A，它不包含周期点，使得对A中任意两个不同的点x₀和y₀，分别从它们出发的对应迭代点的距离数列

|fⁿ(x₀) - fⁿ(y₀)|

当n趋向于无穷大时，其下极限为0，而上极限大于0。

(iii)对A中任意一点x₀及f的任一周期点p，分别从它们出发的对应迭代点的距离数列

|fⁿ(x₀) - fⁿ(p)|

当n趋向于无穷大时，上极限大于0。

推论   若连续函数f有周期-3点，则李-约克定理成立。

该推论可以这样证明：设{a, b, c}是f的一个周期-3轨道，则f³(a) = a。若a < b < c或a > b > c，则李-约克定理的假设成立。若a < c < b或a > c > b，则周期-3轨道{b, c, a}满足b > c > a或b < c < a；若b < a < c或b > a > c，则周期-3轨道{c, a, b}满足c > a > b或c < a < b。所以定理的假设依然成立。

在混沌领域，具有周期三点的两个最著名也最简单的混沌连续函数，一个是与洛伦茨方程关系特别密切、在洛伦茨的《确定性的非周期流》文中露过脸的帐篷映射T: [0, 1] → [0, 1]，其图象是底为单位线段[0, 1]、高为1的等腰三角形的两腰之并，它的周期-3轨道是{2/7, 4/7, 6/7}；另一个是二次多项式函数q(x) = 4x(1-x)，它恰是梅倾心数值迭代的逻辑斯蒂映射族{μx(1-x)}中参数μ取最大允许值4时“最混沌”的那个，它的周期-3轨道是{sin²(π/7), sin²(2π/7), sin²(4π/7)}。这两个最具代表性的混沌科学的案例都分别出自两个杰出的混沌科学家。

在打算用浅显语言论证李-约克定理结论(i)之前，我先解释一下结论(ii)和(iii)中出现的三个数学概念：不可数、上极限及下极限。“不可数”的反义词是“可数”。一个集合如果其所有元素的个数与所有自然数的个数一样多，即这些元素可以像自然数那样排成一个无穷序列，则这个集合被称为是可数的。反之，如果一个集合的元素个数比所有的自然数还要多，同时又至少和所有的无理数一样多，那么我们就说这个集合是不可数的。所有的实数全体，即把所有的有理数和所有的无理数放在一起，是不可数的。同样地，任意两个不同实数之间的所有实数也是不可数的。

定理的后两个结论用到了数列的上极限和下极限概念，它们与理工科大学生熟悉的极限概念密切相关，但一般出现在数学系使用的《数学分析》或《高等微积分》教科书里。一个有界的无穷数列可能不收敛，因而它不一定有极限，如正1与负1交替出现的数列{(-1)^n-1}。但根据实数理论中有名的定理——波尔查诺-魏尔斯特拉斯定理，有界数列总有收敛的子数列，其中所有收敛子数列极限中的最大值一定存在，这个数称之为给定数列的上极限，同样，所有收敛子数列极限中的最小值也一定存在，称之为所给数列的下极限。因此数列{(-1)^n-1}的上极限为1，而下极限为-1。一个数列收敛的充分必要条件是它的上极限等于下极限。

不太熟悉上极限、下极限概念的读者可以这样直观地理解李-约克定理中的结论(ii)：在n趋向于无穷大的过程中，分别对应于相异初始点x₀和y₀的迭代点fⁿ(x₀)和fⁿ(y₀)无穷多次地相互靠近，即它们之间的距离数列有个子数列收敛到0（“彼此吸引”），却又无穷多次地相互离开，即它们之间的距离数列有个子数列收敛到一个大于0的数（“彼此排斥”）。李-约克定理说明，存在比所有的自然数还要多的初始点x₀，不仅由它们出发的迭代点数列 {fⁿ(x₀)} 不可能收敛，而且它们的最终性态也是不可预测的，其主要特征表现在迭代点轨道对于初始条件的敏感依赖性。

因为定理的结论(iii)中的p代表了所有的周期点，这也隐含A中没有周期点。结论(iii)本质上说，距离数列{|fⁿ(x₀) – fⁿ(p)|}不可能趋向于0。因为{fⁿ(p)}是一条周期轨道，这就意味着非周期轨道{fⁿ(x₀)}不是渐近周期的，即它不能趋向于任一条周期轨道。周期轨道的最终性态是可以预测的，而从A中任一点x₀出发的迭代点轨道的最终走向是不可预测的。

李-约克定理中的那个不可数集合A也常被称为一个“乱序集”，这里的“乱序”是英文过去分词scrambled的翻译。一对点 x 和 y 被叫作乱序，如果将给定的函数重复应用于这对点，它们会靠得更近，然后分开，然后靠得更近，然后分开，等等，从而使它们可以任意地相互靠近，但又不可能永远靠得很近。人生中这样的经历很多，比如经常吵架的夫妻好起来的时候可以“亲密无间”，但一旦因小事导致彼此怒目而视就可能离得远远的。这和炒鸡蛋是类似的现象，因此英语词组scrambled eggs的中文翻译是“炒鸡蛋”。常在家中厨房里大炒鸡蛋的动力系统学者可能最善于吸取李-约克混沌的精髓！如果一个集合的任意两个不同的点都是乱序的，则称该集合是乱序的。这样，李-约克定理结论的第二部分可以简写为“存在定义域内一个不可数的乱序集。”

现在，我开始证明定理的结论(i)，但先证明其中n = 1的特殊情形，让读者热一热身后慢慢进入角色。然后我们考虑一般的情形，但如同李天岩教授所倡导并于2017年他一生中最后一次亲手实践的那样，我不对大于 1的任意自然数n求证，而只对n = 4证之，因为思想的火花全在这里闪烁。记b = f(a)，c = f(b)及d = f(c)。我只证明：若d ≤ a < b < c，则f具有一个周期为4的周期点。希望好学的读者读完证明后，用类似的方法补证：若d ≥ a > b > c，则同样的断言也对。

证明的基础是初等微积分里关于连续函数的“介值定理”；约克教授已在《返朴》文章《一个考分总拿C的学生是如何成为著名数学家的？》给出了该定理的证明。没有学过它的人也会懂得它的几何意义：定义在闭区间[a, b]上的一个连续函数的图象，如果其两端点各在x-轴的一边，则它一定穿过x-轴。翻译成代数语言，就是：如果闭区间[a, b]上的连续函数f满足f(a)f(b) < 0，则f在开区间(a, b)内一定有零点。这条性质有一重要的推论：连续函数将定义域中的区间映成区间。换言之，设I是连续函数f定义域的一个子区间，则它在f下的像f(I) = {f(x): x∈I}也是一个区间。这里数学符号“∈”表示“属于”，即它左边的x是它右边I的一个元素。区间具有“连通性”：如果一个区间包含两点u < v，则它包含闭区间[u, v]。这个性质将会像变魔术一般地在后面李-约克定理的证明中多次被玩。

介值定理的另一个推论是著名的布劳威尔不动点定理在一维情形时的特例：若定义在[a, b]上的连续函数f的值域f([a, b])包含在[a, b]内，则f在[a, b]中有不动点。要证明它，定义连续函数g(x) = f(x) – x。显然g(a) = f(a) – a ≥ 0及g(b) = f(b) – b ≤ 0。若a或b是f的不动点，则推论得证，否则的话，必有g(a)g(b) < 0，故由介值定理，开区间(a, b)内某个p是g的零点，它就是f的不动点。

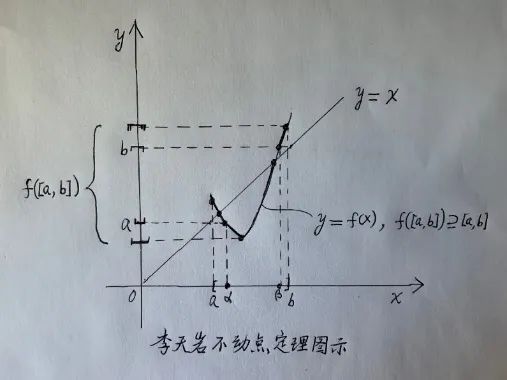
上面众所周知的不动点定理在这里用不上，于是，博士生李天岩为了完成导师的光荣任务，用介值定理又造出一个不动点定理：若定义在[a, b]上的连续函数f的值域f([a, b])包含[a, b]，则f在[a, b]中有不动点。下面我来证明这个“李天岩不动点定理”：

由假设，闭区间[a, b]是值域区间f([a, b])的子集，故数a和b都在f([a, b]) 中，因而存在[a, b]中的两个数α和β，使得a = f(α)及b = f(β)。既然α和β属于[a, b]，就有如下的小于或等于关系：a ≤ α ≤ b及a ≤ β ≤ b。定义连续函数g(x) = f(x) – x，则

g(α) = f(α) - α = a – α ≤ 0，   g(β) = f(β) - β = b – β ≥ 0。

这样，介值定理保证在α和β之间有f的不动点（可能为α或β）。因为以α和β为两端点的闭区间[α, β]或[β, α]是[a, b]的子区间，这个不动点属于[a, b]。证毕。

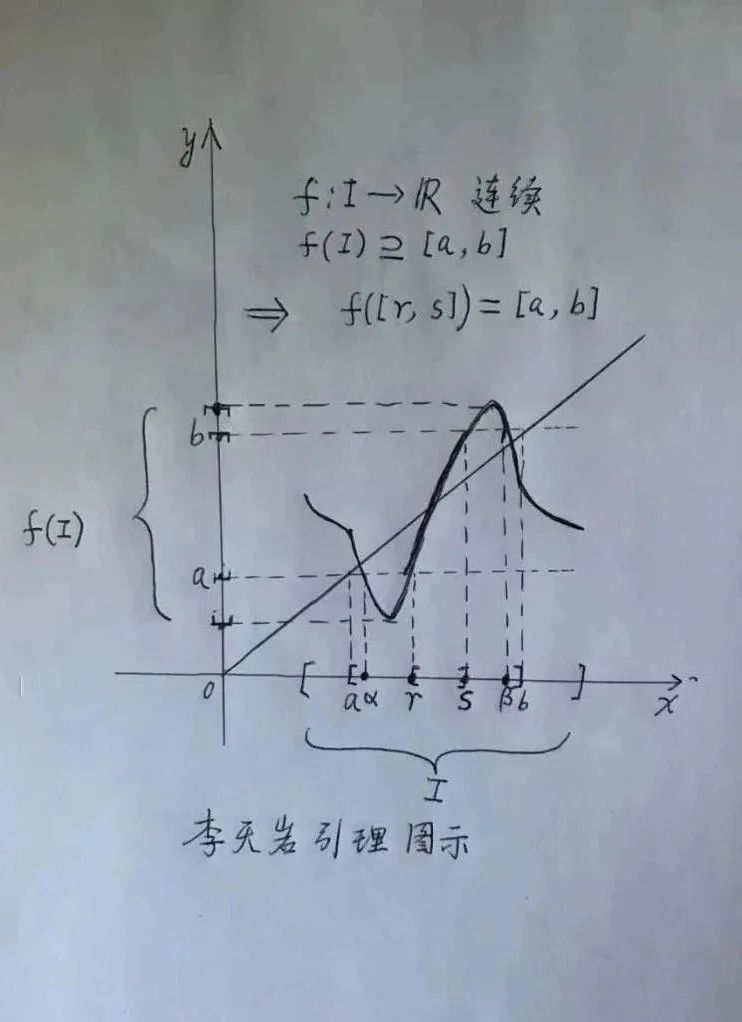
李天岩只需想出最后一个“引理”就可以证明“约克猜想”为真了。它是：设f是闭区间I上的连续函数且[a, b]包含在值域f(I)之中，则I包含一个闭区间J使得f(J) = [a, b]。这里我称它为“李天岩引理”，它在后面关于李-约克定理结论(i)内n = 4时的证明中要被用到三次，而对一般n的情形证明时则要用n-1次，所以必须要证出它：

因为f(I)包含[a, b]，所以存在I中的两点α和β使得f(α) = a及f(β) = b。设α < β。令r为[α, β]中所有满足等式f(r) = a的r中最靠近β的那个。它存在的理由是：如果只有有限个等式f(r) = a，那么最靠近β的那个r一定存在（这和命题“有限个实数中有最大数”是同一个道理），如果有无穷多个这样的等式，则需要更高深一点的论据了：存在单调递增数列{r_n}一步步向β挺进且满足f(r_n) = a，由单调收敛定理知{r_n}收敛到极限r，因为f是连续函数，在恒等式f(r_n) ≡ a中取n趋于无穷大时的极限，就有f(r) = a，这个r最靠近β。然后，出于同样的理由，在r和β之间满足f(s) = b的所有s中取最靠近r的那个。令J = [r, s]，则f(J) = [a, b]。读者可用类似的论据对第二种情形α > β写下证明。证毕。

好了，我们的装备齐全了，可以攻克李-约克定理结论(i)。先证f有不动点，这相对简单。采用该定理的所有符号，从假设f(b) = c和f(c) = d ≤ a < b < c及区间的连通性，可得如下关系

f([b, c]⊇[d, c]⊇[b, c]，

其中符号“⊇”表示其左边的集合包含右边的集合。故由上述的李天岩不动点定理，连续函数f在区间[b, c]中有一个不动点。

现证f有一个周期为4的周期点。我们的策略是在区间[b, c]中找到一点p，满足f⁴(p) = p。由上一段，f([b, c]⊇[b, c]，故根据李天岩引理，存在[b, c]的闭子区间，记为J₁，使得f(J₁) = [b, c]。取此等式两边集合在f下的像，就有

f²(J₁) = f([b, c]⊇[b, c]。

第二次用李天岩引理，就存在J₁的闭子区间，记为J₂，使得f²(J₂) = [b, c]。将f作用到此等式两边，换用新的区间包含关系，得到

f³(J₂) = f([b, c]⊇[d, c]⊇[a, b]。

第三次用李天岩引理，就能找到J₂的闭子区间，记为J₃，使得f³(J₃) = [a, b]。再将f作用于此等式，同时由定理假设f(a) = b及f(b) = c，我们发现

f⁴(J₃) = f([a, b])⊇[b, c]⊇J₁⊇J₂⊇J₃。

这时，李天岩不动点定理派上用场：由包含关系f⁴(J₃)⊇J₃，存在一点p∈J₃，使得f⁴(p) = p。剩下的事是证明f(p), f²(p)及f³(p)都不会等于p，因而p是f周期为4的周期点。只需验证f(p)∈[b, c], f²(p)∈[b, c]以及f³(p)∈[a, b)就足够了，因为这样的话，p不可能是周期小于4的周期点。为什么？假如p的周期为1，则p = f(p)∈[b, c]及p = f³(p)∈[a, b)，但由于[a, b)与[b, c]的交集为空，导致矛盾；假如p的周期为2，则p = f²(p)∈[b, c]，故f(p) = f³(p) 既属于[b, c]，又属于[a, b)，还是矛盾；假如p的周期为3，则p = f³(p)∈[a, b)，但p∈J₃⊆[b, c]，又是矛盾。

现在验证f(p)∈[b, c], f²(p)∈[b, c]和f³(p)∈[a, b)。前两个性质由已证的关系式

p∈J₃⊆J₂⊆J₁⊆[b, c],  f(J₁) = [b, c],  f²(J₂) = [b, c]

直接推得。因为f³(J₃) = [a, b],  我们有f³(p)∈[a, b]。如果f³(p) = b，则p = f⁴(p) = f(b) = c，由此 f(p) = f(c) = d ≤ a。然而，上面刚已证明f(p)∈[b, c]，这就走向f(p) ≤ a < b ≤ f(p)的矛盾。

综上所述，p是f的一个周期为4的周期点。证毕。

上面对于n = 4的证明思想对于一般n情形的李-约克定理结论(i)之证明别无二样。此外结论(ii)和(iii)的证明思路依然出自上面，不过其演算过程更为繁复，我也不想多花读者的时间了，感兴趣者可以阅读李-约克原始论文的附录2。

有趣的是，李-约克定理中的条件无论是“深受束缚”的“周期三点存在”还是“放任自由”的“不等式假设”，定理的证明完全一样，但后者更广的条件就将“李-约克定理关于周期-n点的存在性结论是沙可夫斯基定理的特例”这一非真判断扫进了垃圾堆。某些关于离散动力系统的教科书在讲到周期点时只提沙可夫斯基定理，不提李-约克定理，作者或许就中了这个论断的毒。

十一年前，当我撰写科普著作《智者的困惑——混沌分形漫谈》时，曾与李天岩教授通信请教几个历史事件的来龙去脉。他在给我的一封信件中这样比较李-约克定理和沙可夫斯基定理：

“我们定理的更一般假设和沙可夫斯基的序列有一个很大的不同，可是这在应用上却有极大的差距。好比说在种群动力学上，种群的第一代和第二代都是在增长，但是在第三代却突然大降，于是乎什么‘鬼现象’都可能发生，但是第三代的种群数要降到和第一代一模一样（意指周期三点存在）恐怕不大可能。从这个角度来看，沙可夫斯基序列也许比较适合放在象牙塔里。”

这里“象牙塔”的意思是为追求数学之美而研究数学，但罔顾其与自然界的深层关系。沙可夫斯基定理确实是离散动力系统这一门现代数学科目中的漂亮结果，但它也折射出一部分数学家的哲学理念。他们为了数学的光荣而做数学，以“数学无用”而自豪。他们当中最著名的代表人物就是上世纪英国杰出的纯粹数学家哈代 (Godfrey Harold Hardy，1877-1947)。他在经典随笔《一个数学家的辩白》(A Mathematician’s Apology) 中称那些在工程技术中应用广泛的微积分是“缺乏美学价值的数学”，在他眼里，最美的数学是没有用途的。然而，正是微积分学中的介值定理，敲出了自然界中“周期三”的外壳紧紧裹住的“拟随机硬核”。

这个表达确定性系统拟随机性的数学名词“混沌”首次被李-约克论文所创建。后人将在周期三的背景下产生的混沌特指为“李-约克混沌”，以别于从80年代起离散动力系统教科书中出现的更广泛并且更标准的“混沌”定义。一个常采用的定义如下：函数f: [a, b] → [a, b]被称为是混沌的，如果它在定义域上具有对初始条件的敏感依赖性，或它在所有的非最终周期点上都具有正的李雅普诺夫指数。这个著名的指数是关于对初始条件敏感依赖性的一个量化。也有一个“强混沌”定义：混沌函数f: [a, b] → [a, b]被称为是强混沌的，如果它是传递的，并且所有的周期点在定义域中是稠密的。说f是“传递的”，意思是任给定义域内的非空开区间U和V，其中U被f一次次搬运后的“像序列”f(U), f²(U), f³(U), f⁴(U), …不可能都不与V相交，换句话说，存在正整数n，使得fⁿ(U)和V有共同的元素。说周期点在定义域中是“稠密的”，意思是定义域中任一点x的任意小的一个“开邻域”(x-ε, x+ε)，都包含f的周期点。从这两个数学形容词的解释中就能窥见在强混沌中，迭代过程的有序性态与无序性态纠缠不清的一片混战状况。不过也应当指出，当今并没有“放之四海而皆准”的统一的混沌定义，就如同至今也缺乏“什么是数学”的完美回答一样。