本文讨论分数阶微积分、重整化群和机器学习之间的三元关系。重整化群表征系统在临界点附近的自相似性。分数阶微积分是对函数进行非整数阶积分和微分的定量分析,是解释自相似性或复杂性的另一种工具,两者的关键联系是逆幂律,这对研究复杂系统至关重要。结合分数阶微积分、重整化群,可以提高机器学习算法的泛化性能、增强训练数据多样性、推动最优随机性的研究。文章认为,机器学习的未来应该是物理启发式的,嵌入因果关系或发现因果关系,以及使用分数阶微积分和重整化群,使建模更接近真实本质。
本论文由张江老师推荐,全文翻译自“A New Triangle: Fractional Calculus, Renormalization Group, and Machine Learning”。
撰文 | Haoyu Niu, YangQuan Chen, Lihong Guo, Bruce J. West
翻译 | 宛舒
论文题目:
A New Triangle: Fractional Calculus, Renormalization Group, and Machine Learning
论文链接:
目录
一、分数阶微积分
二、重整化群
三、机器学习
四、分数阶微积分与重整化群
五、分数阶微积分与机器学习
六、重整化群与机器学习
七、新的分数阶微积分-重整化群-机器学习三元关系及新机遇
八、总结
摘要
随着对复杂性的系统化研究不断深入,科学界越来越认识到,牛顿物理学所依赖的基本假设在大部分科学领域中都并不成立,例如,时间不一定是沿着一个方向均匀流动的,空间也不一定是均匀的。本文讨论分数阶微积分(Fractional Calculus,FC)、重整化群(Renormalization Group,RG)理论和机器学习(Machine Learning, ML)如何在研究牛顿形式主义(formalism)的基本假设被违反的不同现象中各自独立发展。
分数阶微积分已经被证明可以帮助我们更好地理解复杂系统,提高复杂信号的处理能力,增强复杂网络的控制能力,提高优化性能,甚至扩大创造力的潜能。重整化群理论允许人们在不同尺度上研究动力系统的变化。例如,在量子场论中,计算的发散部分可能导致无意义的无穷大结果。然而,通过应用重整化群,发散部分可以被吸收到更少的可测量量中,从而得到有限结果。迄今为止,机器学习是一个热门的研究课题,可能在可预见的未来依然如此。如何让一个模型高效(最优)地学习始终是至关重要的。可学习性的关键在于设计高效的优化方法。尽管对这三个主题进行了大量研究,但很少有研究涉及分数阶微积分、重整化群和机器学习领域之间的三元关系。为了推动这三个领域之间相互关系的研究,在本文中作者讨论了它们之间的关键联系(图1)。
在分数阶微积分和重整化群中,标度律揭示了讨论的现象的复杂性。作者强调,分数阶微积分和重整化群之间的关键联系是逆幂律(inverse power laws)的形式,逆幂律指数提供了衡量复杂性水平的方法。对于分数阶微积分和机器学习,关键联系是大数据中的可变性、优化和非局部模型。作者介绍了无导数和基于梯度的优化方法,并解释了分数阶微积分如何为这些研究领域做出贡献。最后,也解释了重整化群和机器学习之间的关联。互信息、特征提取和局部性也被讨论。许多交叉研究表明,重整化群和机器学习之间存在联系。重整化群与深度神经网络(DNNs)结构有表层的相似性,即特征边缘化于隐藏自由度中。作者在结论中指出,分数阶微积分、重整化群和机器学习之间稳固的三元关系,为复杂科学未来的研究课题提供了一个坚实基础。
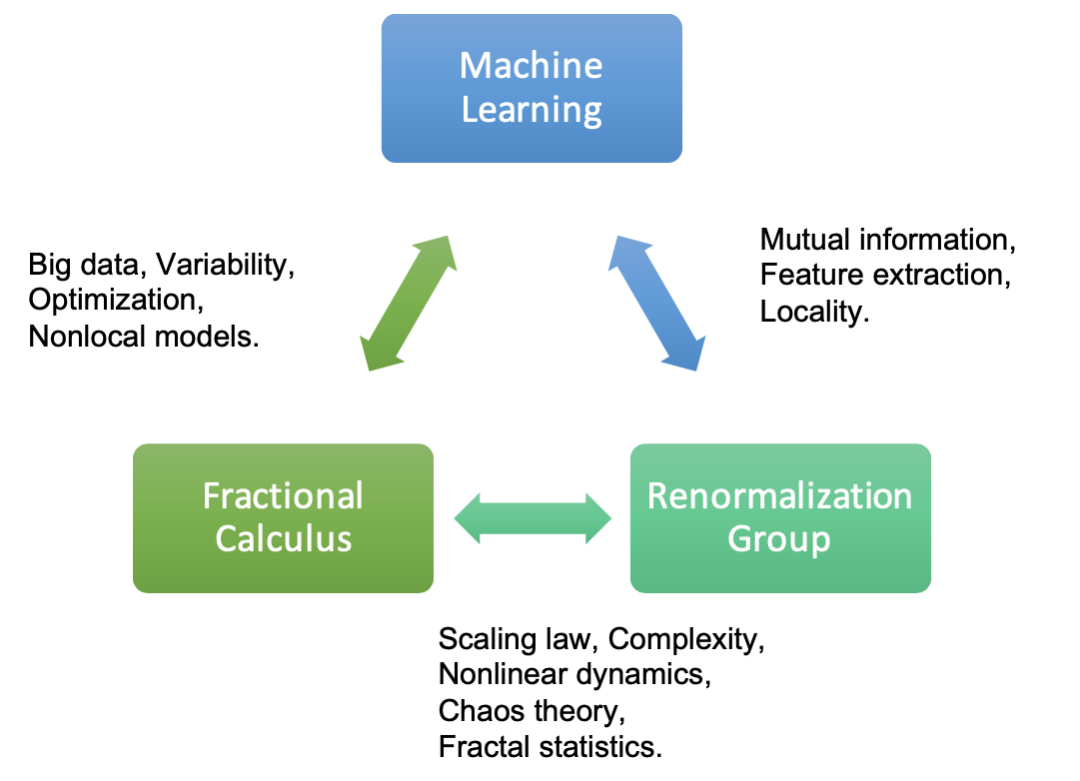
图1. 分数阶微积分、重整化群和机器学习的三元关系示意图。对于FC和RG,文中讨论了标度律和复杂性。作者指出FC和RG之间的核心联系是幂律。对于FC和ML,文中描述了大数据、可变性、优化和非局部模型中的关键联系。作者介绍了无导数和基于梯度的优化方法,并解释了FC如何为这些研究领域做出贡献。最后,解释了RG和ML之间的关联。随后讨论了互信息、特征提取和局部性。许多横向研究表明RG和ML之间存在联系。RG与DNNs结构有表面上的相似性,其中一个边缘化隐藏了自由度。
一、分数阶微积分
分数阶微积分是对函数进行非整数阶积分和微分的定量分析。阶数可以是实数、复数,甚至是变量的函数。关于非整数阶微分的意义的第一次记录出现在1695年洛必达(Guillaume de l'Hôpital)写给莱布尼茨(Gottfried Wilhelm Leibniz)的一封信中。莱布尼茨与牛顿是同时代人,并与他各自独立但共同发明了无穷小微积分[1]。从那时起,许多贡献者为分数阶导数和积分提供了定义[2],几个世纪以来,分数阶微积分的理论及其应用得到了很大的扩展[3, 4, 5]。
在近几十年里,分数阶动力学的概念在统计物理和化学物理领域得到了发展和关注[6, 7, 8]。例如,通过使用分数阶微分和分数阶偏微分方程,最优图像处理得到了改进,Chen 等人进行了总结[9, 10, 11]。异常扩散在[12,13]中使用分数阶扩散方程进行描述,Metzler 等人使用分数阶朗之万方程(Langevin equation)对粘弹性材料进行建模[14]。
分数阶思维(Fractional-order thinking,FOT),是使用分数阶微积分进行思考的一种方式。例如,在整数之间有非整数。在逻辑0和逻辑1之间,有模糊逻辑[15]。与整数阶样条(integer-order splines)相比,有分数阶样条[16]。在高阶整数矩之间,有非整数阶矩。许多研究领域都包含了分数阶思维,例如,自相似[17, 18]、无标度或标度不变性、幂律、长程相关(long-range dependence,LRD)[19, 20],以及1/fα噪声[21, 22]。
二、重整化群
重整化群(Renormalization group,RG)是一个概念框架,包含多种技术,如实空间重整化群[23],泛函重整化群[24],密度矩阵重整化群(DM重整化群)[25]。重整化群最初是在粒子物理学中被发明的。Stueckelbe等人[26]在量子场论中预见并首次从概念上提出了重整化群。他们指出,重整化群展示了一组从裸项到抵消项的变换。迄今为止,重整化群已经扩展到许多其他领域,如固体物理、流体力学和物理宇宙学。在理论物理中,重整化群是一种形式化的工具,允许研究者探讨物理系统在不同尺度上的变化。尺度上的变化通常定义为尺度变换(scale transformation)。
重整化群与自相似性密切相关。在量子场论中,计算中的发散部分可能导致非物理性的无穷大结果。使用重整化群,可以将发散部分重新定义为少量可测量的量,从而得到有限的结果。例如,量子场论用于计算量子水平上基本力的影响。在量子电动力学中,电子可以不断地发射和再吸收“虚拟”光子,这意味着其总能量和总质量可以是无穷大的。然而,使用重整化群理论可以解决发散问题,也就是将包含这些虚拟过程的“裸”电子的质量定义为测量质量。受量子电动力学理论成功的启发,其他一些量子场论也在蓬勃发展,如电弱理论和量子色动力学。然而,一个能够涵盖所有基本力(如引力)的可重整化理论(renormalizable theory)仍在研究中。
除了上述未提及的两个主要研究领域外,动力学系统的混沌行为和统计力学中临界点的普适性理论,尚且没有体现重整化群的必然性。较近期的研究是将重整化群应用于描述复杂动态网络的相变,在临界点处,物理可观测量变得不连续。社会和生物复杂动态网络尽管是有限维的,但它们都被证明是伊辛普适类的成员(Ising Universality class),因此在过去应用中不使用热力学极限。关于这个问题,可以参考 West 等人论文[27]进行的更详细讨论。利用这些思想,研究者[28]开发了一个认知的两级模型,并提供了洞见,说明线性逻辑思维如何被悖论破坏,只能用分数阶思维来解决。
三、机器学习
机器学习(Machine Learning,ML)是让计算机能够从数据中学习的科学(及“艺术”)[29]。1997年,Tom Mitchell 给出了机器学习一个更侧重于工程的定义[30]:“一个计算机程序可以从经验 E 中学习关于某个任务 T 和某个性能度量 P,如果它在任务 T 上的性能(通过 P 测量)随着经验 E 的提高而改善,那么它被认为从经验 E 中学习了。” 2006年,Hinton 等人[31]训练了一个深度神经网络来识别手写数字,准确率超过98%。从那时起,研究人员对深度学习(DL)的兴趣越来越浓厚,这种热情扩展到机器学习的许多领域,如图像处理[32,33]、自然语言处理[34],甚至精准农业[35, 36, 37]。
为什么我们需要机器学习?总的来说,机器学习算法通常可以简化解决方案,并比传统方法表现更好,而传统方法可能需要更多的手动调整规则。此外,传统方法可能无法为复杂现象找到正确的解决方案。机器学习技术可以帮助解释这种复杂性,并更好地适应新数据。机器学习算法可以获取关于复杂问题和大数据的可变性[38]。
机器学习算法的分类有许多不同的类型和方法(图2)。根据是否包含人类监督,机器学习可以分为有监督、无监督、半监督和强化学习(RL)。根据机器学习算法是否能够在线学习,它们可以分为在线学习和批量学习。根据机器学习算法是否检测训练数据模式并创建预测模型,机器学习可以分为基于实例的学习和基于模型的学习[29]。
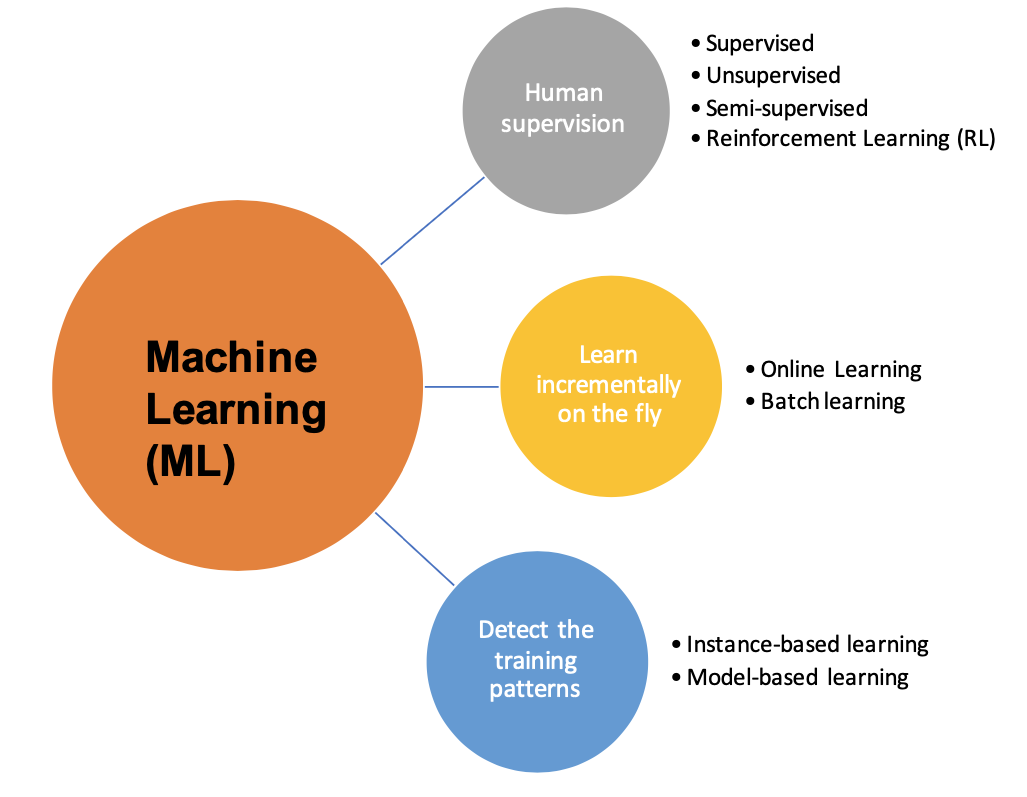
图2. 根据是否包含人类监督,机器学习可以分为监督学习、无监督学习、半监督学习和强化学习。根据机器学习算法是否能够实时增量学习,可以分为在线学习和批量学习。根据机器学习算法是否能检测训练数据模式并创建预测模型,机器学习可以分为基于实例的学习和基于模型的学习[29]。
大多数机器学习算法通过求解依赖于一阶导数(雅可比矩阵)的优化问题来进行训练,这些导数决定了权重是增加还是减少。为了获得巨大的速度提升,人们使用更快的优化器,代替传统的梯度下降(Gradient Descent,GD)优化器。例如,最受欢迎的优化器有动量优化[39]、Nesterov加速梯度[40]、AdaGrad[41]、RMSProp[42]和Adam优化[43]。二阶优化方法(海森矩阵)通常具有更快的收敛速度,但计算成本更高。因此,回答以下问题非常重要:什么是更优的机器学习算法?如果导数是分数阶而不是整数阶,会发生什么?
在这方面的研究仍然有待深入。分数阶导数可能在某些情况下为优化过程提供新的见解和更好的性能。使用分数阶导数的梯度优化方法可能会导致更有效的学习算法,特别是在处理具有复杂结构的数据时。然而,为了在机器学习中成功应用分数阶微积分,需要进一步研究和开发相关方法。这可能包括对现有算法的调整,以便适应分数阶导数,以及开发新的分数阶优化方法,以在机器学习任务中实现更高效的学习。
四、分数阶微积分与重整化群
在相变和临界现象的研究中,重整化群可以成功地表征临界点附近系统的自相似性[44]。由于分数阶微积分是解释自相似性或复杂性的另一种工具,因此分数阶微积分和重整化群之间可能存在强烈的联系。Guo 等人[45]通过讨论带有标度律(scaling law)和复杂现象的重整化群,从不同学科中涵盖了非线性动力学、混沌理论、分形统计和分数阶微积分,以更好地理解它们之间的关系。
幂律通常被描述为:
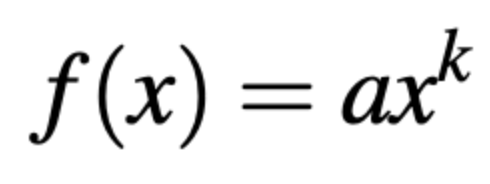
当k为负常数时, f(x)是一种逆幂律。这个幂律的一个重要特性是标度不变性[46],由以下公式确定:
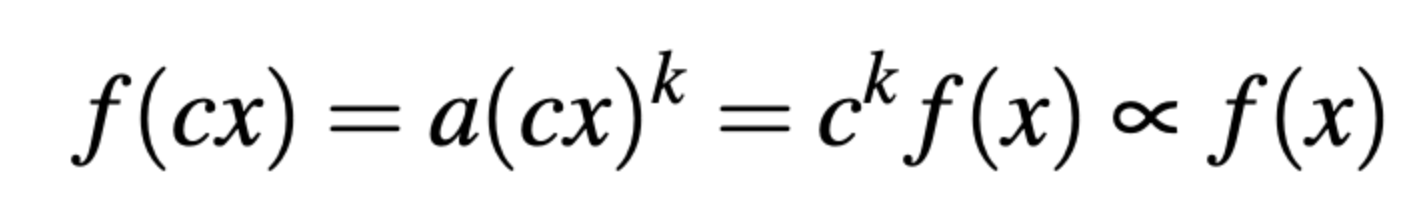
注意,当x是时间时,标度描述了系统动力学的性质。然而,当系统是随机的时候,标度是概率密度函数(probability density function,PDF,或相关结构)的性质,是系统整体性质的约束。
当研究复杂性时,我们会问它意味着什么?研究者在何时开始将系统、网络或现象视为“复杂”[47,48]?似乎我们还不知道一个清晰、统一的对“复杂性”的定义。分数阶微积分和重整化群的联合使用可能会回答以下两个问题[45]:
1.我们该如何描述复杂性?
2.为了更好地理解现实世界的复杂现象,应该使用什么方法来分析复杂性?
在科学界的很大一部分人中达成了共识,当与所研究过程相关的数据分布是逆幂律时,现象就是复杂的。在West和Grigolini的书中[49],有一个表格列出了过去两个世纪发现的经验幂律和逆幂律的样本。例如,在无标度网络中,连通性的度分布遵循逆幂律[50,51];在包含粉红噪声的信号处理中,功率谱是逆幂律[20]。对于其他例子,如概率密度函数、自相关函数(auto-correlation function,ACF)[52]、异速生长(Y=aXb)[53]、异常弛豫(随时间演变)[54]、异常扩散(均方耗散与时间的关系)[13]、自相似,它们都可以用逆幂律来描述。
Douglas[55]研究了表面相互作用聚合物模型,并使用分数阶微积分获得了配分函数的精确解。此外,Douglas首次解释了重整化群标度函数与精确标度函数之间的基本关联。Qian[56]解释了分数布朗运动(fractional Brownian motion,FBM)与统计物理中的重整化群之间的关系,并分析了复杂现象的统计、几何和分形性质。为了证明分数阶微积分与重整化群之间的联系是逆幂律,Guo 等人[45]举了一个维尔斯特拉斯随机游走(Weierstrass Random Walk,WRW)[57]的例子。然后,将重整化群方法应用于晶格结构函数,确定了维尔斯特拉斯随机游走的标度性质。Zaslavsky[58]使用非可积哈密顿量研究混沌粒子动力学。为了解释分形时空系统中随机游走的整体行为,导出了分数Fokker-Planck-Kolmogorov(FFPK)方程。通过使用重整化群方法求解FFPK方程。
五、分数阶微积分与机器学习
如前所述,机器学习是一个热门的研究课题,并可能会在未来一段时间内保持热门。机器如何高效(最优化)地学习始终很重要。学习过程的关键是优化方法。因此,设计一种高效的优化方法有助于回答以下三个问题:
1.最佳优化方式是什么?
2.有没有更优的优化方法?多个最优解?
3.我们能否要求“更优的机器学习”,例如,用最少/最小的标注数据进行深度学习?
在机器学习的过程中,我们关心过程的速度和准确性。算法很重要,否则,数据标注和其他劳动力可能会产生很高的成本。因此,机器学习的关键是所采用的优化方法。收敛速度和全局搜索是优化方法的两个重要部分。从理论上讲,有两大类优化方法,即无导数方法和基于梯度的方法。对于无导数方法,有直接搜索技术,包括粒子群优化(PSO)[59,60]等。对于基于梯度的方法,有梯度下降(GD)及其变种。如下所示,当使用分数阶微积分时,这两类方法都表现出更好的性能。
对于无导数方法(derivative-free methods),有单个代理搜索和基于群体的搜索方法。探索通常通过随机性或根据一些预定义的概率密度函数产生的随机数来实现。利用局部信息如梯度,在局部区域进行更密集的搜索,这种强化可以提高收敛速率。那么问题来了:什么是最优随机性?Wei 等人[61]研究了基于群体的搜索中的最优随机性。四种渐近重尾概率密度函数,即米塔格-累夫勒(Mittag-Leffler)分布、帕累托(Pareto)分布、韦伯(Weibull)分布和柯西(Cauchy)分布,已被用于样本路径分析。根据实验结果,随机性增强的布谷鸟搜索(cuckoo search)算法[62, 63, 64]能够更有效、更稳健地识别分数阶系统的未知特定参数。随机性增强的布谷鸟搜索算法可被视为解决实际复杂优化问题的有前途的工具。原因是在探索过程中,应用了分数阶噪声的最优随机性,这比改良的粒子群优化、布谷鸟搜索都更优。分数阶噪声是指稳定的概率密度函数[65]。换句话说,在讨论最优随机性时,我们在讨论分数阶微积分[66]!
梯度下降是一种非常常用的优化算法,它可以通过迭代调整参数以最小化代价函数来找到最优解。随机梯度下降在训练过程中随机选择时间。因此,代价函数会上下波动,平均而言是减少的,这有助于从局部最优解中逃脱。有时候噪声会被加入到梯度下降方法中,而通常这样的噪声遵循文献中的高斯概率密度函数。我们问:“为什么不是重尾概率密度函数?”这个问题的答案可能引领未来有趣的研究。
发展高效学习过程的关键是优化方法。因此,设计一种高效的优化方法非常重要。无导数方法以及基于梯度的方法,如 Nesterov 加速梯度下降(NAGD),都可以为这个研究领域作出贡献。对于Nesterov 加速梯度下降,Jordan 研究[67]的一个主要思想是在连续时间域中分析迭代算法。对于微分方程,可以使用 Lyapunov 或变分方法来分析其性质,例如收敛速率为 O(1/t²)。人们还可以使用变分方法来推导出优化方法的主微分方程,例如最小作用原理[68],哈密顿变分原理[69]和量子力学路径积分方法[70]。
Jordan 的工作揭示了可以将迭代(优化)算法转换为其连续时间极限情况,这可以简化分析(Lyapunov 方法)。可以直接设计一个运动微分方程(equation of motion ,EOM),然后将其离散化以导出迭代算法(变分方法)。关键是找到合适的 Lyapunov 泛函来分析稳定性和收敛速率。Jordan 揭示的新奇事实是,优化算法可以使用拉格朗日力学(欧拉-拉格朗日方程)、运动微分方程系统地合成。
受 M. Jordan 在频域的思想启发,研究者在[38]中设计了一个连续时间分数阶系统。此外,根据内部模型原则(internal model principle ,IMP),在 S 或 Z 变换域中设计和分析机器学习算法是可行的[38]。总的来说,M. Jordan 提出了这个问题:“有没有最优的优化方法?”我们的回答是肯定的,通过限制动力学分析、离散化和结合其他随机性的随机梯度下降,例如朗之万运动。这里提出的问题是:“有没有更优的优化方法?”答案仍然是肯定的,但需要使用分数阶微积分来优化随机梯度下降、随机搜索和内部模型原则中的随机性。沿着这个思路,还有更多的潜力可以进行进一步的研究。
非局部模型通常用于描述不能通过经典方法准确描述的物理系统和(或)过程[71]。例如,分数非局部麦克斯韦方程和相应的分数波动方程已经在研究[72]中应用于分数矢量微积分[73]。非局部微分算子[74],包括梯度/海森矩阵的非局部模拟,是这些非局部模型的关键,这可能在不久的将来与分数阶微积分一起成为非常有趣的研究。
六、重整化群与机器学习
机器学习研究的目标是从训练数据中学习并提取重要特征。作为机器学习的一个子领域,深度学习使用多层表征直接从训练数据中学习特征,这在许多研究主题中取得了成功,如精准农业[75, 76, 77]和目标检测[78, 79, 80]。尽管深度学习算法取得了成功,但关于为什么机器学习技术在特征学习上表现良好的证据仍然很少。
最近,一些横向交叉研究表明重整化群与机器学习之间存在关联[81,82,83]。Jefferson 指出,重整化群与机器学习之间的联系最初是在某些晶格模型(lattice models)的背景下建立的[84]。抽取重整化群,与抽取深度神经网络(深度神经网络)结构,表面上具有相似性,即结构特征被边缘化在隐藏自由度中。例如,Mehta 等人提出,机器学习算法可能使用类似于广义重整化群的方案从数据中学习特征[82]。在深度神经网络中,低级特征被输入到具有更抽象高级特征的更高层。在特征提取过程中,深度神经网络学会忽略无关特征,保留相关特征。这种连续粗粒化过程类似于重整化群,它通过整合短距离自由度来提取物理系统的相关特征,以描述大尺度现象。为了说明他们的观点,他们基于受限玻尔兹曼机构建了变分重整化群和深度学习架构之间的映射。
Lin 等人[83]探讨了如何将物理性质(如对称性、局部性、可组合性和多项式对数概率)转化为神经网络。他们认为,当统计过程属于物理和机器学习中常见的某种层次结构形式时,深度神经网络可以比浅层网络表现得更好。例如,物理学的一个原则是局部性,即事物只直接影响其紧邻区域。当在机器学习应用中考虑局部性时,一组局部随机变量的任意变换将导致非局部集合[83]。然而,局部性可以保留。例如,在简单的块自旋(block-spin)重整化群中,自旋被分组成块,然后被视为随机变量。根据高精度,这些块仅与其最近邻相互耦合。这种局部性通常被生物和人工视觉系统所利用。然而,较低层只执行较局部的操作。
在物理系统中,通用性质大多数时候可以决定物理特性,这可以通过重整化群程序揭示。然而,关键的自由度可能不容易找出。因此,Koch-Janusz 等人提出了一种基于模型无关的、信息论特征的人工神经网络,用于实空间重整化群过程[85]。基于机器学习算法,该模型可以识别空间区域内的物理相关自由度,并迭代地执行重整化群粗粒化步骤。输入数据遵循玻尔兹曼分布,并且不提供关于系统的微观细节的进一步知识。神经网络的参数通过基于评估空间分离区域之间的实空间互信息(real-space mutual information,RSMI)的训练算法来优化。二维经典统计物理中的伊辛模型和二聚体模型被用于方法验证。
七、新的分数阶微积分-重整化群-机器学习
三元关系及新机遇
总的来说,作者在本文中讨论了分数阶微积分、重整化群和机器学习之间的联系。证明了分数阶微积分、重整化群和机器学习之间存在一种新的三元关系。本节将展示关于把分数阶微积分与重整化群和物理知识联系起来的未来研究机会。
1. 泛化
通过分数阶微积分、重整化群和机器学习,可以提高泛化性能(generalization)。机器学习模型具有很大的潜力可以得到提升,尤其是将泛化部分与分数阶微积分和重整化群方法联系起来。例如,Mehta 等人提出,机器学习算法可能采用了一种类似于广义重整化群的方案来从数据中学习特征[82]。整个复杂系统通常有许多小组件,它们可以与附近的组件和环境相互作用,使得它们的行为难以预测。因此,集合概率密度函数动力学不能用相空间中的标准偏微分方程描述。概率密度函数方程被确定为传统相空间方程的分数阶泛化[45]。
2.训练数据集的可变性和多样性
可变性(variability)是训练机器学习算法过程中讨论的最关键的特征。可变性可以指训练数据集的几个属性。首先,需要使用异常和离群值检测方法了解数据中的不一致性数量。其次,可变性也可以指多样性(diversity)[86, 87],这是由于不同数据类型和来源产生的,例如健康或不健康[88, 89]。如前所述,对于重整化群方法,在量子场论中,计算的发散部分可能导致无意义的无穷大研究结果。通过应用重整化群,发散部分可以吸附到较少的可测量量中,产生有限的结果。重整化群和分数阶微积分技术可以增强机器学习算法的训练数据多样性。反过来,在相同性能要求下,我们可以期望“小数据”而不是“大数据”。
3.加速学习
在深度神经网络中,低级特征被输入到具有更抽象高级特征的更高层神经网络中。在特征提取过程中,深度神经网络可以学会忽略无关特征,保留相关特征,从而使学习过程更快、更高效。如前所述,这个过程类似于重整化群,它通过整合短距离自由度来提取物理系统的相关特征,以描述大尺度现象。为了说明这个想法,Mehta 等人[82]根据受限玻尔兹曼机构建了变分重整化群和深度学习架构之间的映射。机器学习算法可以从重整化群和分数阶微积分中受益。
4.最优随机性
随机性在探索和应用方面都起着重要作用。具有良好随机分配权重的神经网络架构可以轻松胜过具有精细调整权重的更糟糕的架构[90]。因此,使用重整化群和分数阶微积分方法讨论机器学习算法的最优随机性至关重要。对于分数阶微积分,随机性有丰富的形式[91],例如重尾性,它对应于分数阶主方程[92]。在概率论中,重尾分布(heavy-tailed distributions)是其尾部不呈指数衰减的分布[93]。因此,它们的尾部比指数分布的尾部有更高的权重。重尾分布广泛用于不同学科的建模,如金融[94]、保险[95]和医学[96]。
在[83]中,Lin 等人探讨了如何将物理性质与重整化群方法结合起来,在神经网络中进行转换。在[85]中,Koch-Janusz 等人提出了一种基于实空间重整化群过程的模型无关的、信息论特征的人工神经网络。基于机器学习算法,该模型可以识别空间区域中的物理相关自由度,并迭代地执行重整化群粗粒化步骤[85]。我们相信,这些示例可以为使用分数阶微积分、重整化群和机器学习一起研究最优随机性打开新的视野。
八、总结
分数阶微积分、重整化群和机器学习是三个最具生产力的研究领域,可能在不久的将来仍然如此。关于这三个主题的研究已经进行得相当广泛。然而,很少有研究探讨了分数阶微积分、重整化群和机器学习之间的三元关系。因此,作者在本文中阐述了三元关系中的关键联系。
在处理复杂系统时,揭示和解释了分数阶微积分和重整化群之间的联系。对于分数阶微积分和重整化群,讨论了标度律和复杂性,这里我们注意到解决分数扩散方程的概率密度函数的标度形式[43]。作者指出,分数阶微积分和重整化群之间的关键联系是逆幂律,这对研究复杂系统至关重要。
对于分数阶微积分和机器学习,描述了大数据、可变性、优化和非局部模型中的关键联系。作者介绍了无导数优化方法和基于梯度的优化方法,并解释了分数阶微积分如何为这些研究领域做出贡献。分数阶动力学响应了更高级的表征,以捕捉以前被平滑处理的过小或过大尺度的结构,进而应对我们所面对的更复杂的世界。假设一个希望获得比使用整数阶微积分方法可能达到的最佳结果还要好的结果,或者希望“更优化”,我们主张应用分数阶思维。在大数据时代,决策和控制需要分数阶微积分,例如分数阶信号、系统和控制。
最后,解释了重整化群和机器学习之间的关联。讨论了互信息、特征提取和局部性。许多交叉研究表明重整化群和机器学习之间存在联系。重整化群与深度神经网络结构相似,即特征边缘化于隐藏自由度中。机器学习的未来应该是物理启发式的、科学的(嵌入因果关系或发现因果关系)以及涉及使用分数阶微积分和重整化群,使建模更接近真实本质。
参考文献
Vinagre, B. M., and Chen, Y., 2002. “Lecture notes on fractional calculus applications in automatic control and robotics”. In Proceedings of the 41st IEEE CDC Tutorial Workshop, Vol. 2, pp. 1–310.
Vale ́rio, D., Machado, J., and Kiryakova, V., 2014. “Some pioneers of the applications of fractional calculus”. Frac- tional Calculus and Applied Analysis, 17(2), pp. 552–578.
Abel, N., 1823. “Solution of a couple of problems by means of definite integrals”. Magazin for Naturvidenskaberne, 2(55), p. 2.
Podlubny, I., Magin, R. L., and Trymorush, I., 2017. “Niels Henrik Abel and the birth of fractional calculus”. Frac- tional Calculus and Applied Analysis, 20(5), pp. 1068– 1075.
Ross, B., 1977. “The development of fractional calculus 1695–1900”. Historia Mathematica, 4(1), pp. 75–89.
Tarasov, V. E., 2011. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media.
Springer Science & Business Media. Klafter, J., Lim, S., and Metzler, R., 2012. Fractional Dy- namics: Recent Advances. World Scientific.
Pramukkul, P., Svenkeson, A., Grigolini, P., Bologna, M., and West, B., 2013. “Complexity and the fractional calcu- lus”. Advances in Mathematical Physics, 2013, pp. 1–7.
Chen, D., Xue, D., and Chen, Y., 2013. “More optimal im- age processing by fractional order differentiation and frac- tional order partial differential equations”. In Proceedings of the International Symposium on Fractional PDEs.
Chen, D., Sun, S., Zhang, C., Chen, Y., and Xue, D., 2013. “Fractional-order TV-L 2 model for image de- noising”. Central European Journal of Physics, 11(10), pp. 1414–1422.
Yang, Q., Chen, D., Zhao, T., and Chen, Y., 2016. “Frac- tional calculus in image processing: A review”. Fractional Calculus and Applied Analysis, 19(5), pp. 1222–1249.
Seshadri, V., and West, B. J., 1982. “Fractal dimen- sionality of Le ́vy processes”. In Proceedings of the Na- tional Academy of Sciences of the United States of America, 79(14), p. 4501.
Metzler, R., and Klafter, J., 2000. “The random walk’s guide to anomalous diffusion: A fractional dynamics ap- proach”. Physics Reports, 339(1), pp. 1–77.
Metzler, R., Glo ̈ckle, W. G., and Nonnenmacher, T. F., 1994. “Fractional model equation for anomalous diffu- sion”. Physica A: Statistical Mechanics and its Applica- tions, 211(1), pp. 13–24.
Metzler, R., Glo ̈ckle, W. G., and Nonnenmacher, T. F., 1994. “Fractional model equation for anomalous diffu- sion”. Physica A: Statistical Mechanics and its Applica- tions, 211(1), pp. 13–24.
Unser, M., and Blu, T., 2000. “Fractional splines and wavelets”. SIAM Review, 42(1), pp. 43–67.
Samoradnitsky, G., 2017. Stable non-Gaussian Random Processes: Stochastic Models with Infinite Variance. Rout- ledge.
Crovella, M. E., and Bestavros, A., 1997. “Self-similarity in World Wide Web traffic: Evidence and possible causes”. IEEE/ACM Transactions on Networking, 5(6), pp. 835–846.
Burnecki, K., and Weron, A., 2004. “L´evy stable processes. From stationary to self-similar dynamics and back. An application to finance”. Acta Physica Polonica Series B, 35(4), pp. 1343–1358.
Pesquet-Popescu, B., and Pesquet, J. C., 2002. “Synthesis of bidimensional a-stable models with long-range dependence”. Signal Processing, 82(12), pp. 1927–1940.
Hartley, T. T., and Lorenzo, C. F., 2003. “Fractionalorder system identification based on continuous orderdistributions”. Signal Processing, 83(11), pp. 2287–2300.
Wolpert, R. L., and Taqqu, M. S., 2005. “Fractional Ornstein–Uhlenbeck L´evy processes and the telecom process: Upstairs and downstairs”. Signal Processing, 85(8), pp. 1523–1545.
Kadanoff, L. P., 1966. “Scaling laws for Ising models near Tc”. Physics Physique Fizika, 2(6), pp. 263–272.
Wetterich, C., 1993. “Exact evolution equation for the effective potential”. Physics Letters B, 301(1), pp. 90–94.
White, S. R., 1992. “Density matrix formulation for quantum renormalization groups”. Physical Review Letters, 69(19), pp. 2863–2866.
Stuckelberg, E., 1953. “La normalisation des constantes dans la theorie des quanta”. Helvetica Physica Acta, 26, pp. 499–520.
West, B. J., Turalska, M., and Grigolini, P., 2014. “Complex networks: From social crises to neuronal avalanches”. Hoboken, NJ: Wiley-VCH Verlag GmbH, pp. 509–524.
West, B. J., 2019. “Paradox entails new kinds of medical knowledge”. Medical Research Archives, 7(8), pp. 1–16.
G´eron, A., 2019. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems. O’Reilly Media.
Mitchell, T. M., 1997. Machine Learning. McGraw-hill New York.
Hinton, G. E., Osindero, S., and Teh, Y. W., 2006. “A fast learning algorithm for deep belief nets”. Neural Computation, 18(7), pp. 1527–1554.
Zhao, T., Yang, Y., Niu, H., Wang, D., and Chen, Y., 2018. “Comparing U-net convolutional network with mask R-CNN in the performances of pomegranate tree canopy segmentation”. In Proceedings of the Multispectral, Hyperspectral, and Ultraspectral Remote Sensing Technology, Techniques and Applications VII, International Society for Optics and Photonics.
Zhao, T., Koumis, A., Niu, H., Wang, D., and Chen, Y., 2018. “Onion irrigation treatment inference using a lowcost hyperspectral scanner”. In Proceedings of the Multispectral, Hyperspectral, and Ultraspectral Remote Sensing Technology, Techniques and Applications VII, International Society for Optics and Photonics.
Hirschberg, J., and Manning, C. D., 2015. “Advances in natural language processing”. Science, 349(6245), pp. 261–266.
Zhao, T., Niu, H., de la Rosa, E., Doll, D., Wang, D., and Chen, Y., 2018. “Tree canopy differentiation using instance-aware semantic segmentation”. In Proceedings of the 2018 ASABE Annual International Meeting, American Society of Agricultural and Biological Engineers.
Niu, H., Zhao, T., Wang, D., and Chen, Y., 2019. “A UAV resolution and waveband aware path planning for onion irrigation treatments inference”. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), IEEE, pp. 808–812.
Niu, H., Wang, D., and Chen, Y., 2020. “Estimating crop coefficients using linear and deep stochastic configuration networks models and UAV-based normalized difference vegetation index (NDVI)”. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), IEEE.
Niu, H., Chen, Y., and West, B. J., 2021. “Why do big data and machine learning entail the fractional dynamics?”. Entropy, 23(3), p. 297.
Polyak, B. T., 1964. “Some methods of speeding up the convergence of iteration methods”. USSR Computational Mathematics and Mathematical Physics, 4(5), pp. 1–17.
Nesterov, Y., 1983. “A method for unconstrained con- vex minimization problem with the rate of convergence O(1/k2)”. Doklady Akademii Nauk, Russian Academy of Sciences, 269, pp. 543–547.
Duchi, J., Hazan, E., and Singer, Y., 2011. “Adaptive sub- gradient methods for online learning and stochastic opti- mization.”. Journal of Machine Learning Research, 12(7), pp. 2121–2159.
Hinton, G., and Tieleman, T. Slide 29 in lecture 6, 2012, rmsprop: “Divide the gradient by a running average of its recent magnitude”.
Kingma, D. P., and Ba, J., 2014. “Adam: A method for stochastic optimization”. arXiv preprint arXiv:1412.6980.
Wilson, K. G., 1983. “The renormalization group and crit- ical phenomena”. Reviews of Modern Physics, 55(3), pp. 583–600.
Guo, L., Chen, Y., Shi, S., and West, B. J., 2021. “Renor- malization group and fractional calculus methods in a com- plex world: A review”. Fractional Calculus and Applied Analysis, 24(1), pp. 5–53.
Kello, C. T., Brown, G. D., Ferrer Cancho, R., Holden, J. G., Linkenkaer Hansen, K., Rhodes, T., and Van Orden, G. C., 2010. “Scaling laws in cognitive sciences”. Trends in Cognitive Sciences, 14(5), pp. 223–232.
West, B. J., Geneston, E. L., and Grigolini, P., 2008. “Maxi- mizing information exchange between complex networks”. Physics Reports, 468(1-3), pp. 1–99.
West, B. J., 2020. “Sir Isaac Newton stranger in a strange land”. Entropy, 22(11), p. 1204.
West, B. J., and Grigolini, P., 2010. Complex Webs: Antici- pating the Improbable. Cambridge University Press.
Baraba ́si, A. L., and Albert, R., 1999. “Emergence of scal- ing in random networks”. Science, 286(5439), pp. 509– 512.
Sun, W., Li, Y., Li, C., and Chen, Y., 2011. “Conver- gence speed of a fractional order consensus algorithm over undirected scale-free networks”. Asian Journal of Control, 13(6), pp. 936–946.
Li, M., 2007. “Modeling autocorrelation functions of long- range dependent teletraffic series based on optimal approx- imation in Hilbert space—A further study”. Applied Math- ematical Modelling, 31(3), pp. 625–631.
Zhao, Z., Guo, Q., and Li, C., 2008. “A fractional model for the allometric scaling laws”. The Open Applied Mathe- matics Journal, 2(1), pp. 26–30.
Sun, H., Chen, Y., and Chen, W., 2011. “Random-order fractional differential equation models”. Signal Processing, 91(3), pp. 525–530.
Douglas, J. F., 1989. “Surface-interacting polymers: An integral-equation and fractional-calculus approach”. Macromolecules, 22(4), pp. 1786–1797.
Qian, H., 2003. “Fractional Brownian motion and fractional Gaussian noise”. In Processes with Long-Range Correlations. Springer, pp. 22–33.
Hughes, B., Montroll, E., and Shlesinger, M., 1982. “Fractal random walks”. Journal of Statistical Physics, 28(1), pp. 111–126.
Zaslavsky, G., 1994. “Renormalization group theory of anomalous transport in systems with Hamiltonian chaos”. Chaos: An Interdisciplinary Journal of Nonlinear Science, 4(1), pp. 25–33.
Wei, J., Yu, Y., and Wang, S., 2015. “Parameter estimation for noisy chaotic systems based on an improved particle swarm optimization algorithm”. The Journal of Applied Analysis and Computation, 5(2), pp. 232–242.
Wei, J., Yu, Y., and Cai, D., 2018. “Identification of uncertain incommensurate fractional-order chaotic systems using an improved quantum-behaved particle swarm optimization algorithm”. Journal of Computational and Nonlinear Dynamics, 13(5).
Wei, J., Chen, Y., Yu, Y., and Chen, Y., 2019. “Optimal randomness in swarm-based search”. Mathematics, 7(9), p. 828.
Wei, J., and Yu, Y., 2019. “A novel cuckoo search algorithm under adaptive parameter control for global numerical optimization”. Soft Computing, pp. 1–24.
Wei, J., Chen, Y., Yu, Y., and Chen, Y., 2019. “Improving cuckoo search algorithm with Mittag-Leffler distribution”. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, pp. 1–9.
Wei, J., and Yu, Y., 2018. “An adaptive cuckoo search algorithm with optional external archive for global numerical optimization”. In Proceedings of the International Conference on Fractional Differentiation and its Applications (ICFDA).
Gorenflo, R., and Mainardi, F., 1998. “Fractional calculus and stable probability distributions”. Archives of Mechanics, 50(3), pp. 377–388.
Niu, H., Wei, J., and Chen, Y., 2021. “Optimal randomness for stochastic configuration network (SCN) with heavytailed distributions”. Entropy, 23(1), p. 56.
Wilson, A. C., Recht, B., and Jordan, M. I., 2016. “A Lyapunov analysis of momentum methods in optimization”. arXiv preprint arXiv:1611.02635.
Feynman, R. P., 2005. “The principle of least action in quantum mechanics”. In Feynman’s Thesis—A New Approach to Quantum Theory. World Scientific, pp. 1–69.
Hamilton, S.W. R., 1834. On a General Method in Dynamics. Richard Taylor.
Hawking, S. W., 1979. “The path-integral approach to quantum gravity”. In General Relativity: An Einstein cen- tenary survey. pp. 746–789.
Nagaraj, S., 2020. “Optimization and learning with nonlo- cal calculus”. arXiv preprint arXiv:2012.07013.
Tarasov, V. E., 2008. “Fractional vector calculus and frac- tional Maxwell’s equations”. Annals of Physics, 323(11), pp. 2756–2778.
Ortigueira, M., and Machado, J., 2018. “On fractional vectorial calculus”. Bulletin of the Polish Academy of Sciences: Technical Sciences, 66(4), pp. 389–402.
Feliu Faba, J., Fan, Y., and Ying, L., 2020. “Meta-learning pseudo-differential operators with deep neural networks”. Journal of Computational Physics, 408, p. 109309.
Niu, H., Zhao, T., Westphal, A., and Chen, Y., 2020. “A low-cost proximate sensing method for early detection of nematodes in walnut using Walabot and scikit-learn classification algorithms”. In Proceedings of the Autonomous Air and Ground Sensing Systems for Agricultural Optimization and Phenotyping V, International Society for Optics and Photonics.
Niu, H., Zhao, T., Zuber, C., Vasquez-Mendoza, J., Doll, D., Arnold, K., and Chen, Y., 2020. “A low-cost stem water potential monitoring method using proximate sensor and scikit-learn classification algorithms”. In Proceedings of the ASABE Annual International Virtual Meeting, American Society of Agricultural and Biological Engineers, pp. 1–6.
Niu, H., Hollenbeck, D., Zhao, T., Wang, D., and Chen, Y., 2020. “Evapotranspiration estimation with small UAVs in precision agriculture”. Sensors, 20(22), p. 6427.
Niu, H., Zhao, T., and Chen, Y., 2019. “Intelligent bugs mapping and wiping (iBMW): An affordable robotdriven robot for farmers”. In Proceedings of the IEEE International Conference on Mechatronics and Automation (ICMA), IEEE, pp. 397–402.
Wang, Y., Niu, H., Zhao, T., Liao, X., Dong, L., and Chen, Y., 2019. “Contactless Li-Ion battery voltage detection by using Walabot and machine learning”. In Proceedings of the ASME 2019 International Design Engineering Technica Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers Digital Collection.
Wang, Y., Chen, Y., Liao, X., and Dong, L., 2019. “Lithium-ion battery face imaging with contactless Walabot and machine learning”. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), IEEE, pp. 1067–1072.
B´eny, C., 2013. “Deep learning and the renormalization group”. arXiv preprint arXiv:1301.3124.
Mehta, P., and Schwab, D. J., 2014. “An exact mapping between the variational renormalization group and deep learning”. arXiv preprint arXiv:1410.3831.
Lin, H. W., Tegmark, M., and Rolnick, D., 2017. “Why does deep and cheap learning work so well?”. Journal of Statistical Physics, 168(6), pp. 1223–1247.
Jefferson, R., 2019. Deep learning and the renormalization group. Available online at the website of: (Accessed: 4th August 2019).
Koch Janusz, M., and Ringel, Z., 2018. “Mutual information, neural networks and the renormalization group”. Nature Physics, 14(6), pp. 578–582.
Nakahira, Y., Liu, Q., Sejnowski, T. J., and Doyle, J. C., 2019. “Diversity-enabled sweet spots in layered architectures and speed-accuracy trade-offs in sensorimotor control”. arXiv preprint arXiv:1909.08601.
Arabas, J., and Opara, K., 2019. “Population diversity of non-elitist evolutionary algorithms in the exploration phase”. IEEE Transactions on Evolutionary Computation, 24(6), pp. 1050–1062.
Ko, M., Stark, B., Barbadillo, M., and Chen, Y., 2015. “An evaluation of three approaches using Hurst estimation to differentiate between normal and abnormal HRV”. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers.
Li, N., Cruz, J., Chien, C. S., Sojoudi, S., Recht, B., Stone, D., Csete, M., Bahmiller, D., and Doyle, J. C., 2014. “Robust efficiency and actuator saturation explain healthy heart rate control and variability”. Proceedings of the National Academy of Sciences, 111(33), pp. E3476–E3485.
Scardapane, S., and Wang, D., 2017. “Randomness in neural networks: An overview”. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, Volume 7(2).
Montroll, E. W., and West, B. J., 1979. “On an enriched collection of stochastic processes”. Fluctuation Phenomena, 66, p. 61.
Li, Z., Liu, L., Dehghan, S., Chen, Y., and Xue, D., 2017. “A review and evaluation of numerical tools for fractional calculus and fractional order controls”. International Journal of Control, 90(6), pp. 1165–1181.
Asmussen, S., 2003. “Steady-state properties of GI/G/1”. Applied Probability and Queues, pp. 266–301.
Bernardi, M., and Petrella, L., 2015. “Interconnected risk contributions: A heavy-tail approach to analyze US financial sectors”. Journal of Risk and Financial Management, 8(2), pp. 198–226.
Ahn, S., Kim, J. H., and Ramaswami, V., 2012. “A new class of models for heavy tailed distributions in finance and insurance risk”. Insurance: Mathematics and Economics, 51(1), pp. 43–52.
Resnick, S. I., 2007. Heavy-tail Phenomena: Probabilistic and Statistical Modeling. Springer Science & Business Media.
本文经授权转载自微信公众号“集智俱乐部”。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 