1979年,我国理论物理学家、相对论研究的资深专家张元仲先生出版了《狭义相对论实验基础》,这本经典著作曾广为中国物理学人研读。在张先生去世前几年,此书经他本人再次修订,目前得以再版。本书详细介绍了各种狭义相对论实验检验及结果,并在厘析历史事实方面做了精准解读,对正确理解物理学概念和理论发展起到关键性作用。在分析实验方面取材广泛,涉及光学、天文学实验、高能物理、原子物理等多个领域,可为不同背景的专业人士提供实验基础解释。该书附录中包含的几篇澄清狭义相对论基本概念的研究论文,也有利于读者更好地学习和更准确理解相对论。
撰文 | 张元仲
1.坐标系与同时性定义
狭义相对论和经典力学一样,是以惯性定律为基础的,就是说它只适用于惯性系。惯性系就是那些使惯性定律在其中有效的坐标系。惯性定律可以表述为:不受力的物体将保持静止或做匀速直线运动的状态。但是,何为“匀速”,并未给出严格的定义。因为我们只有对同时性给予明确无误的定义之后,才能描述物体的速度。事实上,“速度”并非直接测量量,它是空间的距离和时间间隔的比值。我们可以依靠标准尺应用欧几里得几何对空间任意两点的距离进行测量。空间中每一点的“当地时间”可以用置于该点的标准钟的读数给出。然而这还不够,因为定义速度所需要的时间间隔是位于不同地点(不管这两点相距多近)的两只时钟的读数之差。所以我们还得事先将这两只钟调得“同步”,即校准。这就需要不同地点时钟的同时性定义。说是“定义”,是因为我们并没有一种先验的校钟方法。这就是说,每一个惯性坐标系都必须用某种方法将其中各个空间点上放置的相互静止的标准时钟调节成”同步”. 经典力学中的”同步”(或说同时性)是瞬时的。狭义相对论用光信号校钟,并假定光速各向同性。因此,狭义相对论中的惯性系定义与经典力学中惯性系定义之间的唯一差别,在于同时性定义的不同。
2.理论预言与实验数据的比较
首先,我们已经知道这样一个事实,即迄今为止,实验室一般都是使用光信号校准时间的,并假定光速为常数,c≈3×108m/s。这就是说,文献中给出的两地时钟的读数之差或某物体的速度v的数值,都是相对于爱因斯坦同时性定义的。所以,这些数据与狭义相对论的预言比较是直截了当的。然而,我们却不能将这些数值直接同经典力学(以及其他检验理论)的预言进行比较,因为经典力学用的是瞬时同时性的定义。为了与实验数据比较,我们必须使用以下公式:
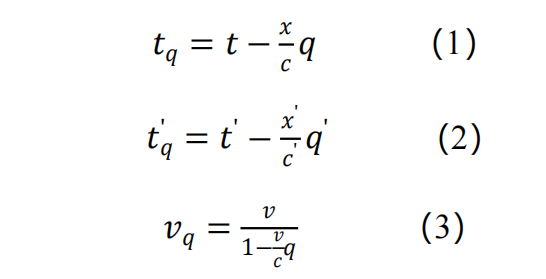
(取q=q'=1,相应于c=c'→∞,瞬时传播信号)
将伽利略变化式(x'=x-vt,t'=t)中的时间t和t'以及速度v转换成可以同实验数据直接进行比较的量:t0、t0'和v0。转换关系是
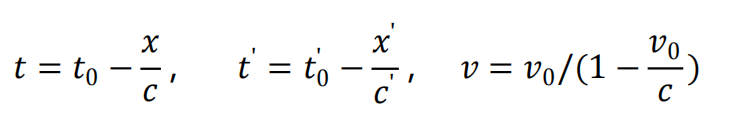
3.时间和空间的概念
狭义相对论虽然改变了经典力学中的时空观念的某些绝对性,但并未从根本上变更。从某些意义上说,狭义相对论的时空观也是一种绝对的时空观。首先,惯性系的建立就需要事先有一个空虚的空间和离开物质而独立存在的时间。说的绝对一点就是:如果物质消失了,还会剩下空间和时间作为表演物理事件的一种舞台。当我们考查一个物体在空虚空间中做匀加速运动时,我们同样会遇到经典力学中的概念问题:惯性运动和加速运动有着严格的区别;加速指的是“对于空间的加速度”,而惯性指的是对加速度的抵抗;这就是说,空间对物质发生作用,而物质对空间没有影响。这也就是牛顿所说的“空间是绝对的”。所以说,狭义相对论中的时间和空间虽然有了某种联系,但仍没有摆脱时空的绝对性(指不受物质影响)。广义相对论对这个问题给出了自己的回答:引力场由时空度规描写,时空度规的源是物质的能量——动量(张量),即物质决定时空;狭义相对论中的闵可夫斯基时空只不过是广义相对论中爱因斯坦方程的一种特殊的解,或者说它是由物质分布所决定的一种特殊形式的引力场,即系统的最低能态(真空态)。
4.狭义相对论的检验理论和单向光速的不可观测性
通过检验光速不变原理和同时性定义的各类实验的详细分析,说明这类实验所检验的不是单向光速而是往返平均光速的不变性。理解这一问题的关键是要认识到这样一个事实,即我们没有先验的同时性定义,而光速的定义又依赖于同时性定义。爱因斯坦从1905年第一篇论文开始,就对这一问题阐述得十分清楚了。后来爱德瓦兹(Edwards)的检验理论又进一步论证了这个问题。尽管如此,我们仍不时在各种文章和某些通俗读物上看到“光速各向同性已被实验证实”诸如此类的臆断[1-5]。其中,最值得一提的是,有些学者使用所谓的曼苏里-塞塞尔(Mansouri-Sexl,简称M-S)检验理论直接同实验数据进行了比较[5]。因此,仔细分析这类检验理论是十分必要的。为此,我同Nester教授进行了讨论,并总结发表了一篇论文 [9],对其主要结果简述如下:
狭义相对论的检验理论有三类:爱德瓦兹变换[6]、罗伯逊(Robertson)变换[7]、曼苏里-塞塞尔变换 [8]。同洛伦兹变换相比较,爱德瓦兹变换只是多了一个方向性参数q(q')。罗伯逊变换中的参数可以用三个新参数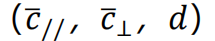 代替,其中参数
代替,其中参数![]() 和
和![]() 分别代表光信号平行和垂直于两惯性系相对运动方向的往返平均速度。M-S变换比罗伯逊变换也是多了一个方向性参数q(q')。所以我们可以知道:在洛伦兹变换中单向光速为各向同性;在爱德瓦兹检验理论中单向光速可变(由q和 q'的非零值表征),而平均往返光速不变
分别代表光信号平行和垂直于两惯性系相对运动方向的往返平均速度。M-S变换比罗伯逊变换也是多了一个方向性参数q(q')。所以我们可以知道:在洛伦兹变换中单向光速为各向同性;在爱德瓦兹检验理论中单向光速可变(由q和 q'的非零值表征),而平均往返光速不变![]() =
=![]() =c;在罗伯逊检验理论中,
=c;在罗伯逊检验理论中,![]() ≠
≠![]() ≠c,且单向光速等于平均光速;在M-S检验理论中,
≠c,且单向光速等于平均光速;在M-S检验理论中,![]() ≠
≠![]() ≠c,且单向光速不等于平均光速而与方向性参数q有关。所以M-S变换对罗伯逊变换的推广恰如爱德瓦兹变换对洛伦兹变换的推广。当把这些变换与物理实验比较时,必须考虑到检验理论中的同时性与实验室通常使用的爱因斯坦同时性定义不同,这种不同已用公式(1)~(3)表达了出来。因此,与实验数据的正确比较会使我们看到,方向性参数q不会在任何物理预言中出现,恰如爱德瓦兹变换在物理上不比洛伦兹变换多任何东西一样。罗伯逊变换(也就是M-S变换)所能检验的是
≠c,且单向光速不等于平均光速而与方向性参数q有关。所以M-S变换对罗伯逊变换的推广恰如爱德瓦兹变换对洛伦兹变换的推广。当把这些变换与物理实验比较时,必须考虑到检验理论中的同时性与实验室通常使用的爱因斯坦同时性定义不同,这种不同已用公式(1)~(3)表达了出来。因此,与实验数据的正确比较会使我们看到,方向性参数q不会在任何物理预言中出现,恰如爱德瓦兹变换在物理上不比洛伦兹变换多任何东西一样。罗伯逊变换(也就是M-S变换)所能检验的是![]() 和
和![]() 的差别,也就是双程平均光速的方向性(因为任意方向上的双程平均光速可以表达成
的差别,也就是双程平均光速的方向性(因为任意方向上的双程平均光速可以表达成![]() 和
和![]() 的函数)。
的函数)。
关于单向光速的方向性问题,我再补充几句。如果我们在自然界中发现大于光速的新信号存在,我们就可以在原则上用新信号校准时钟,从而对单向光速的方向性作出判断。但是新信号的单向光速却成为了一个不可观测的问题。除非我们发现瞬时传播的信号,否则,用于校准时钟的那种(速度最快的)信号的单向速度的问题总是一个无法检验的问题。
参考文献
[1] Aspden H. Proposed method of measuring first-order speed of light anisotropy. Physics Letters A, 1982, 92(4):165-166.
[2] Zhang Y Z the unidirectional speed of light observable?. Physics Letters A, 1983, 95( 5):225-225.
[3] MacArthur D W. Special relativity: understanding experimental tests and formulations. Physical review A, 1986, 33: 1.
[4] Haugan M P, Will C M. Modern tests of special relativity. Physics today, 1987, 40(5): 69.
[5] Will C M. Clock synchronization and isotropy of the one-way speed of light. Physical review D,1992, 45: 403.
[6] Edwards W F. Special relativity in anisotropic space. American journal of physics. Am. J. Phys., 1963, 31(7): 482-489.
[7] Robertson H P. Postulate versus observation in the special theory of relativity . Reviews of modern physics, 1949, 21: 378.
[8] Mansouri R, Sexl R U. A test theory of special relativity. General relativity & gravition, 1977, 8(7): 497-513, 515-524, 808-814.
[9] Zhang Y Z. Test throries of special relativity. General relativity and gravition, 1995, 27: 475-493.
作者简介

张元仲(1940-2022),1965年毕业于中国科学技术大学,1965-1980年在中国科学院物理研究所工作,1980年后在中国科学院理论物理研究所担任研究员、博导。主要研究领域是(广义和狭义)相对论、引力理论与实验、宇宙学、空间基础物理,在国内外学术刊物发表学术论文140余篇,曾获全国科学大会奖状、国家自然科学二等奖、国家教委三等奖、中国科学院科技进步二等奖。
文本出自张元仲著《狭义相对论实验基础》第一版重印说明,略有修改。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 