尼古拉·布尔巴基是20世纪最重要的数学家之“一”，编撰皇皇巨著数十卷《数学原本》（Éléments de mathématique），信奉公理体系与结构主义思想。他也是最神秘的数学家，只闻其声不见其人，在数学江湖中流传着许多关于他的传说。事实上，他是一个虚构的人物，其背后是布尔巴基学派——一群年轻的法国数学家最初为了编写新教材而聚集在一起成立的。创始人之一包括数学巨匠安德烈·韦伊，他在自己的回忆录《一个数学家的学徒生涯》中记下了布尔巴基诞生的时刻。

撰文 | 安德烈·韦伊（André Weil）

翻译 | 吕珊珊、许大昕

布尔巴基的诞生

回到斯特拉斯堡，我又回到了亨利·嘉当（Henri Cartan）和“微积分”课程身边，我们两个一起教这门课，让我得以摆脱“普通数学”的束缚。我们对微积分课程上使用的古尔萨（Édouard  Goursat）编写的教材越来越不满意。由于嘉当不断向我询问怎么教某一节课程更好，我给他起了个绰号叫“十万个为什么法官”（Iinterrogant bailli）。而我也没少向他求助。他当时关心的一点是，我们在教学中应在多大程度上推广斯托克斯（Stokes）公式。

这个公式写作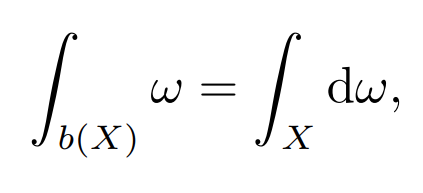

其中 ω 是一个微分形式，dω 是它的导数，X 是它的积分定义域而b(X)是 X 的边界。如果 X 是无穷次可微可定向的球面，ω 是无穷次可微的形式，这个公式并不困难。这个公式的特殊情况出现在经典的论著中，但我们并不满足于此。

埃利·嘉当（Elie Cartan）关于积分不变量（invariants intégraux）的书已经继庞加莱之后展现了这个等式的重要性，并提出要拓展它的应用范围。从数学上讲，这是一个庞大的问题，比我们所能想到的都要大。它在同调理论以及德拉姆（de Rham）的定理中明显都扮演了重要角色，但它不仅与它们相关。这个问题最终打开了分布与流的理论，乃至层论的大门。然而，眼前主要是为了嘉当和我在斯特拉斯堡教学的问题。那是 1934 年末的冬天的一天，我灵光一现，想到一个办法来解决我朋友源源不断的问题。我大概是这样和嘉当说的：“我们五六个朋友都在不同的学校开同样的课。我们一起来彻底把这个问题解决了吧，以后我就不用回答你的问题了。”我当时并不知道布尔巴基就在这一刻诞生了。

如果不是因为这是一个事后重构整合的记忆，如果这段对话就如同我记忆中的那样发生，那么这将会对布尔巴基的个人资料十分重要，因为这可以确定他的出生日期。然而我却不能确定。每个人都知道，哪怕是最明细的记忆，上面都没有刻着日子，而它们自己也不是按照时间顺序排列的。从多个角度来看，记忆都像是一个装满了老照片或一段段胶片的盒子，这些照片和胶片有的都已经半褪色了，我们很难再把它们以不同的形式裁裁剪剪，按时间排列，而就算我们这样做了，也会经常弄错。所以，和历史上的许多伟人一样，布尔巴基的身份资料永远都不能确定。而这再适合他不过了。

同样是在这样的对话里，或者是在一些类似的对话里，我、嘉当、德尔萨特（Jean Delsarte）、舍瓦莱（Claude Chevalley）、迪厄多内（Jean Dieudonné），还有其他的几个人，定时在巴黎会面。我们在圣米歇尔大街的一家餐馆里聚会，这家餐馆现在已经不在了。我上述提到的人都和布尔巴基一起走到了最后，也就是布尔巴基五十岁的时候。这是布尔巴基为自己定下的退休年龄。之后，人们将这些人称为“创始成员”。

布尔巴基也有档案，德尔萨特很早就负责这些了。长久以来，它们被保存在南锡（Nancy）大学的数学系里。现在，它们都在巴黎。然而，不幸的是，关于我所说的这个时期，它们并不是很齐全。于是，在下文我谈到布尔巴基时，主要依靠的还是我的记忆。

布尔巴基创始成员包括亨利·嘉当（后排左一）、安德烈·韦尔（后排右二）和索尔姆·曼德尔布罗伊特 （Szolem Mandelbrojt）（前排最右）。图片来源：Nicolas Bourbaki

揭开谜底

围绕着布尔巴基的名字积累了一系列传说，布尔巴基的合作者们没少在其中出力。是揭开谜底的时候了。在我们的计划变成了一部集体著作的时候，我们觉得不能在封面上写一大串名字。就在这时，我们想起了高师的一个恶作剧。

当德尔萨特、嘉当和我还是高师学生的时候，1923届新进入高师的理科生，都收到了一份抬头是学校官方的纸质通知，上面说某日某时，某个名字带着斯堪的纳维亚味道的教师会做一个讲座，建议大家参加。做讲座的人是一个高年级的学长，名叫拉乌尔·于森（Raoul Husson），爱搞恶作剧。他在成了统计学家后，在音系学和用科学方法研究歌唱的领域占据了一席之地，听说也做出了一些有价值的工作。在1923年，他来到“新生”（conscriti）【译者注：原意为“新兵”，指第一年入学的新生，为巴黎高师学生的黑话。】面前，带着一副假胡子，操着一口难以描述的口音，给他们做了一个报告。报告似乎由一类古典函数理论出发，上升到了夸张的高度，最后以“布尔巴基定理”结束，听众们都惊讶得说不出话来。至少，传说的版本就是这样的，据说还有一个在场的高师学生号称从头到尾都听懂了。

其实我们的学长命名这个定理的灵感来自记忆中拿破仑时代的一个将军。在印度，我给我的朋友科桑比（Kosambi）讲了这个故事。他用这个名字写了一个形式严肃，实则内容滑稽的结果概要（note），想要发表在外省学院的一些院刊（comptes-rendus）上。我们很快就达成共识，让一个布尔巴基来当我们未来作品的作者。之后，还要确定到底是哪个布尔巴基。这个问题在1935年年末被提了出来，大家便决定以一种无法辩驳的方式建立起布尔巴基的存在：以他的名义在科学院的院刊上发表一个结果概要。于是，布尔巴基就需要有一个名字。我未来的妻子艾弗琳（Eveline）在我们讨论的时候在场，她为布尔巴基取名为尼古拉（Nicolas），就这样成了布尔巴基的教母。我们还需要一位科学院的成员去呈交这个结果概要。我们毫不怀疑，如果这件事的风声走漏到科学院的常任秘书埃米尔·皮卡（Emile Picard）那里，他一定会被气得中风。我负责撰写这份结果概要，并附上了一封证明信，发给了埃利·嘉当。

埃利·嘉当对我们的活动和计划心知肚明。我还给他写了一份尼古拉·布尔巴基的小传，说他来自波黑。我特别强调说，科学院的成员在呈交一份结果概要时，应该确保其科研内容的严肃性，而非关注其作者生平的细节。一群科学院的成员通常在每周开会前一起吃午饭，人们一直将其称为“年轻成员的午饭”，其实，他们的青春在很久以前就已然一去不复返了。在喝利口酒的时候，埃利·嘉当向他的同事询问了他们对我的证明信的意见，并获得了他们的同意。至于结果概要的内容，其实并没有什么神奇之处，尽管之后别人和我说里面有个错误。这难道是布尔巴基的诅咒吗？

布尔巴基的祖国是波黑，这其实来自另一个高师学生的恶作剧。据传，大约是在1901年，一些高师的学生在蒙巴纳斯的一些咖啡馆里找来了一些来自不同国家的人。他们把这些人聚集起来，以一些食物作为交换，让他们假装成波黑的代表，他们为这些人写了一些信件，发给政界、文学界和大学领域的名人。信的开头是：“您不会对波黑的苦难一无所知……”人们开始对此表现出一些同情，而到了适当的时候，这些学生召开了公共集会，并为主讲人写了一篇感人至深的讲稿。开篇大概是“于是，我这个波黑议会主席，一个可怜的流亡者，生活在如此的苦痛之中，我连一条裤子都没有。”主讲人说着就爬上了桌子，他的确没有穿裤子。

为了结束这段有关布尔巴基的名字和祖国的插曲，让我讲一个之后发生的事情吧。大约在 1948年，妮可尔·嘉当（Nicole Cartan）在电话里和她的丈夫说：“布尔巴基要和你讲话。”在电话里，亨利·嘉当听到一个声音说：“我的名字是布尔巴基，我想见一下您。”“您是不是有一部大白胡子?”“不，我没有胡子，但我想见您。”嘉当感到十分困惑就同意和他见面。在约定的时间，来了一位衣冠楚楚的先生，一见到嘉当，他就立刻将一本外交护照放在桌子上：尼古拉依德斯·布尔巴基（Nicolaides-Bourbaki），希腊大使馆参赞。他解释道，布尔巴基家族十分出名，可以上溯到17世纪，当时有两兄弟，因为抵抗土耳其人而闻名。在远征埃及时，拿破仑的一个领航员就是一个布尔巴基。作为回报，拿破仑让他的儿子进了拉弗莱什（La Fleche）的普瑞塔尼国家军校（Prytanee）。这个儿子之后成了法国军官，而他的后代就是后来在历史上十分出名的拿破仑三世的将军。尼古拉依德斯·布尔巴基觉得自己对家谱上的人了如指掌，家里没有数学家。究竟为什么别人要用这个名字出版数学著作呢？嘉当向他解释了原因。在这之后的好几年里，他一直都会参加我们会后的聚餐。在1950 年，当我去希腊的时候，他给了我一封信，让我转交他在雅典的亲戚们。他们十分热情地款待了我。我当时没能到克里特岛，真的是太遗憾了。他们和我说，如果我去了的话，当地人一定会给我烤一只羊羔，来向尼古拉·布尔巴基致敬。

以布尔巴基的身份出版著作

为了维持一个作者的身份，这还不够，还需要给他找一个编辑。当时，法国数学出版业的市场由高蒂尔-维拉尔出版社（Gauthier-Villars）控制乃至垄断。但我们也完全没想去向他们求助；在我们看来，这个出版社太学院派了。还好我们也不是必须去找他们，因为一开始我们就找到了编辑，那就是恩里克·弗雷曼（Enrique Freymann）。

这是一个既有吸引力，又十分丰富多彩的人。在二战时，他拯救了我的藏书，把它们藏在了圣日耳曼大街的仓库里。在布尔巴基成型的时候，弗雷曼已经对我们十分熟悉了。或许在我去印度之前，就已经见过他了。在1931年，我和几个朋友都因为雅克·埃尔布朗（Jacques Herbrand）在山中遇难的事情极度悲伤，他的去世在我们之间产生了无法弥补的空洞。大家决定，为了最后再纪念他一次，一起为他写一部文章合集。艾米·诺特（Amalie Noether）、冯·诺伊曼（John von Neumann）和哈塞（Helmut Hasse）也十分愿意加入我们。弗雷曼立即就同意了出版这个集子。他坚持要放在他的《科学与工业时讯》（Actualités Scientifiques et Industrielles）从书中，不单是一册，而是一个系列。从我们和他讲起布尔巴基开始，他就没有过丝毫犹豫。他是我们认定了的编辑。他也信任我们，从一开始就一直鼓励我们，而他并没有为此感到后悔：在未来，布尔巴基成了赫尔曼出版社的财政支柱之一然而，在我所讲的那个年代，做到这一点并不简单。一直有不少索邦出身的“好心人”警告他，说这只是高师学生开的一个粗俗玩笑，他要是上当了，可就太笨了。或许，在很大程度上吸引他参与到我们的计划之中的，正是布尔巴基的名字和传说，他自己也满腔热忧地将它们完善并四处传播。

布尔巴基大会

至于我们的计划的实质到底是什么，其实在我们刚着手去做的时候，也不是很清楚。最开始，我们的目标在某种意义上是为了教学，主要是为本科水平的数学教学理出一些大的脉络来。很快我们就需要编写一本本科水平的分析教材，以便代替古尔萨的教材成为教学的基础。我们在巴黎聚会，主要做的是确定章节的标题并分配任务。布尔巴基会要求其合作者对许多主题进行报告，内容从集合理论一直到解析函数和偏微分方程。而我们也逐渐明白，如果要以合适的广度来讨论这些报告，我们在巴黎的聚会是不够的。大家一致决定，拿出我们暑假中的两周，找一个合适的地方一起度过。克莱蒙（Clermont）大学在贝斯昂尚戴斯（Besse-en-Chandesse）【译者注：今贝斯和圣阿纳斯泰斯（Besse-et-Saint-Anastaise）】有一些很舒服的房子，夏天正好空着。于是，在 1935 年 7月，布尔巴基开了第一次大会。

尽管这个想法在现在十分平常，但是在那个年代却不太常见不久之后，在德国，一些纳粹数学家设想组织一些“工作营”，模仿当时送失业者去劳作的劳动营（Arbeitslager）。之后，这种组织形式在全世界传播开来，无论是在资本主义社会还是在社会主义社会，并且成了将官方资助用于通常十分值得称赞的科研活动的常见方式之一。但从本质上说，这些讲座、会议、研讨会，无论名字是什么，都是一些互助教学小组，尽管之后这些活动的成果会被发表。这从来都不是布尔巴基的合作者们在会议中的目标。布尔巴基的合作者从前聚集在一起，现在也持续聚集在一起，是为了撰写并完善一个集体的工作。不过，这也不是说大家就没有机会从别人那里学到许多东西。毕竟这不是我们的主要目的。

至于大会的资助，在二战前都不成问题。我们是为了自己的兴趣才聚集在一起的，对我们而言，自己承担费用也是很自然的。在1948 年后，考虑到法国当时的状况，大家向洛克菲勒基金会申请了一笔援助。申请获得了批准，大家对此很满意。在此之后，布尔巴基的稿费就足够支付大家的花费了。

布尔巴基大会（1936 年于尚赛，Chançay ）。长椅上：克劳德·舍瓦莱的侄子，从左往右（坐着的）安德烈·韦伊、舍瓦莱的母亲、（站着的）妮奈特·埃雷斯曼（Ninette Ehresmann）、勒内·德波塞（R. de Possel）、克劳德·舍瓦莱、雅克琳娜·舍瓦莱、米尔莱斯（Mirles，外号“小白鼠”）、让·德尔萨特、夏尔·埃雷斯曼（Charles Ehresmann）。

在布尔巴基贝斯昂尚戴斯的大会之后，我需要去沙隆（Chalon）附近的穆尔默隆（Mourmelon）军营参加三周的军训（一“期”军训当时人们是这样说的）。我是后备中尉，在军营里又遇到了我在高师的伙伴们，他们对军旅生活的热情与我相似。如果说我从这段经历中学到了什么的话，那大概是军旅生活的时间主要用在等待上而且晚上睡得很少，白天却一直犯困。我获得了上校的许可，可以提前一两天离开军营，借口是和我一样受邀去莫斯科参加“第一届国际拓扑大会”的法国数学家们会合。上校只问了我一个简单的问题：“你们的小分队由谁指挥？”我急中生智，回答道：“当茹瓦先生，学院院士。”当茹瓦（Arnaud Denjoy）的确也是被邀请赴会的数学家之一。我获得批准，得以先坐飞机去华沙，然后从那里坐火车去莫斯科，也不用去管所谓的“小分队”，及时参加了预定于9月4日至10日召开的会议。多亏了苏联同事的慷慨，我和他们一直待到了 10 月，中间还去参观了一次列宁格勒。

在9月，布尔巴基的成员们聚在一起，开“埃斯科里亚尔大会”，因为这是我们本来打算去开会的地方，如果西班牙内战没有爆发的话。最后是舍瓦莱母亲在她位于图尔奈的尚赛的漂亮房产中接待了我们，这里离武夫赖（Vouvray） 不远。我们一开始想换掉的经典的大部头分析教材，比如若尔当（Camille Jordan）和古尔萨，都试图在很短的篇幅里解释一个数学学习者在钻研这一方向之前需要掌握的东西。在19 世纪末，这还并不是一个荒谬的要求，然而在现在却不行了。仅仅是初步了解群论和一些代数和拓扑的概念，要掌握的东西就远比简单的几章介绍多。在我们着手去做这项工作时，我们并不确定是否要为每个主题都写一部著作，而只是想以尽量大的广度来介绍它们，这样我们之后就不用一直回头重新解释了。然而很快，我们就不得不放弃编写大学教材的主意。无论如何，我们要做的是建立一个足够大、足够牢固的基础，以支撑现代数学所有最基础的东西在基础之上搭建什么建筑，人们尽可以畅想，然而这并不是最紧急的。

在这次和下一次大会，我们就立即制定了工作的方法。每一个主题都会在一个初步报告的基础上并在大会讨论后，指定一个作者。作者会给出一个草稿，在大会上重新宣读并讨论，草稿多多少少会被彻底修改，或是像不止一次发生过的那样，被全部否定。大会将指定另一个作者，根据收到的指示写第二篇稿子，然而很自然地，作者并不会一直遵从指示。之后就以此类推……

这样一来，无论是布尔巴基什么样的文章，署上我们之中任何个人的名字，都显然是不可能的。再说，大家也约定，任何决定都只有全体成员同意才能通过，而所有决定都可以被质疑。或许需要一个牢固的坚信礼（acte de foi），才能让人相信这个程序能够运行，但我们对布尔巴基是有信仰的。尽管如此，当我们第一次能够同意将一个文本送印的时候，我们自己都为此感到惊讶。那是有关集合论的“结果分卷”，在临近战争的时候被最终通过。有关这一主题，第一次是嘉当的一篇文章在“埃斯科里亚尔大会”上宣读。嘉当没有参会，他的文章被拒绝的消息是通过电报发给他的：“并交子集乘积被你肢解了，该死的布尔巴基。”（Union intersection partieproduit tu es démembré foutu Bourbaki.）我们很审慎地决定，不等待之后的详细报告，而是先出版有关集合论的分册：它将给出一些固定的记号（notations）。这些记号应当在一开始给出，之后就不用重提了。事实上，这些修改了许多既定的用法的记号是被相当普遍地认同了的。在很久之后，我在这些讨论中的参与令我赢得了我的女儿妮科莱特（Nicolette）在学习集合论时的尊敬：我告诉她说，我个人与代表空集的符号Ø大有关系。Ø属于挪威字母，而我是布尔巴基里唯一对此有所了解的。

同样是在“埃斯科里亚尔大会”，我们大致确定了之后写作的标准，其中甚至也包含了排版格式。我们的原则是，在每一章后面不仅有不同难度的练习，而且还有一个“历史小论”（laius historique）。它是之后“历史注释”的前身，在很大程度上是这些“历史注释”让我们的作品与众不同。大家采用了这一原则，让我十分满意（因为数学史，或者说对过去伟大数学作品的阅读，很久以来都让我十分心醉）。

在布尔巴基当时即将着手去进行的任务的名单中，结构这一概念以及与之相关的同构的概念的采用，获得了可观的进步。回头再看，这些概念显得平平无奇，在没有被加入态射和范畴的概念时，其数学的内容也十分微薄。在我们做出最初工作的年代，它们是一束新光线，照在了许多当时仍然十分混乱的主题上。“同构”这个词的意思在每个理论里甚至都不同。这里究竟是群的简单结构，还是拓扑空间，乃至于更复杂的结构，从环一直到实数域和拓扑向量空间，就我所知，在布尔巴基之前还没有被说明过，而这些是需要说明的。至于为什么要用结构这个词，我不太记得了。但我认为，在那个年代，这个词已经进入了语言学家的词汇之中，而我一直和这个群体有联系，尤其是和埃米尔·本维尼斯特（Emile Benveniste）。或许这仅仅只是一个巧合。

本文经授权节选自《一个数学家的学徒生涯》（高等教育出版社，2023年9月）第五章《斯特拉斯堡和布尔巴基》，小标题为编者所加。