1805年2月13日，狄利克雷出生在德国迪伦（当时属于法国）的一个普通家庭。狄利克雷的祖父安托万·狄利克雷（Antoine L. Dirichlet）是一位布料制造商，到迪伦发展事业并组建了家庭。狄利克雷的父亲约翰·狄利克雷（Johann A. L. Dirichlet）既是商人也是镇政府官员，先后担任过迪伦的初级议员、市政代表和邮政局长，是一个和蔼又正直的人。母亲安娜·伊丽莎白（Anna Elisabeth）同样出身布商家庭。^[1]狄利克雷是家中最小的孩子，排行第七。由于当时政局动荡，在狄利克雷出生后，全家由法国公民转变为普鲁士公民。

尽管并不富裕，但狄利克雷的父母对他们天赋极高的儿子给予了非常精心的教育。狄利克雷早年在迪伦的一所小学读书，当这所学校不再能满足他对知识的需求时，父母就将他转到了一所私立学校。在那里，他还学习了拉丁语，为进入高中做准备。狄利克雷很早就表现出对数学的喜爱，不到12岁时就已开始用零用钱买数学书了。当被告知他无法理解这些数学书时，他回答说“无论如何我都会读这些书，直到理解为止”。^[2]可见其对数学的热爱。

起初，父母希望他成为一名商人，不过因为狄利克雷更想学习而放弃这一想法，并在1817年送他到波恩高中学习。在波恩高中狄利克雷因勤奋、有礼，很快赢得了周围人的喜欢，并对数学和历史表现出特殊兴趣，历史方面尤其关注法国大革命后的近代历史。

两年后，狄利克雷转到科隆的耶稣会高中，并跟着欧姆（S. Ohm）学习数学，后来欧姆因发现以其名字命名的欧姆定律而闻名。1821年，狄利克雷离开科隆高中，同年8月20日，狄利克雷收到了学校相关负责人签署的证书，证明他是高年级学生，在学习古代语言、数学、历史、物理和德语方面很勤奋，在所有科目上都取得了显著进步，表现良好^[1]。

准备进入大学时，父母又希望狄利克雷学习法律以确保他有一个好的前途。然而，父母的想法由于狄利克雷对数学的喜爱再次夭折，因为狄利克雷表示他会在白天学习法律，在晚上学习数学，所以狄利克雷的父母明智地做了让步。

确定了学习方向后，去哪里学习是当时面临的主要问题。由于当时德国大学的数学水平不高，唯一闻名世界的数学家还是不喜普通教学的高斯，所以狄利克雷决定去巴黎学习，当时的巴黎是世界数学之都。此外，在被法国占领时期，狄利克雷家族的许多老熟人就定居在巴黎或经常访问巴黎，他们可以为16岁的狄利克雷提供必要的帮助，后来也确实帮了他很多。

1822年5月，狄利克雷动身前往巴黎，在当月最后一个星期日抵达后，写信告知父母他将在法兰西学院和巴黎理学院学习。在那里很多顶尖的数学家都成了他的老师，比如毕奥（B. Biot）、傅里叶（J. Fourier）、弗朗科尔（B. Francoeur）、阿谢特（P. Hachette)、拉普拉斯（S. Laplace）、拉克鲁瓦（S. Lacroix）、勒让德（A. Legendre）和泊松（S. Poisson），使狄利克雷获益良多。^[3]

除了学习课程之外，狄利克雷还自学高斯的杰作《算术研究》。来到巴黎后狄利克雷曾请求母亲给他寄几本数学书，其中就包括《算术研究》的副本。狄利克雷一生多次研究《算术研究》，是第一个完全理解它的人。狄利克雷从来不把它放到书架上而是经常放在桌子上，以便随时研究，睡前狄利克雷也会读一些难懂的段落，睡觉时就把书放在枕头下面，希望夜里醒来重读一下就清楚了这些段落^[4]。据说狄利克雷每次旅行时也都带着它，就像一些牧师总是带着自己的祈祷书一样^[2]。

 
《算术研究》

然而，巴黎的求学路并非一帆风顺。1822年秋天，狄利克雷刚到法国不久，巴黎就爆发了大规模流感，数千人感染了天花，狄利克雷也在其中。不过幸好他之前接种了疫苗，降低了病毒的危害，他的名字没有出现在有1000多人的死亡名单上，并且他很快恢复健康，回归课堂。

在巴黎，除了正常学习外，狄利克雷还有另外的机遇。1823年夏，狄利克雷家族的老熟人推荐他去福伊（S. Foy）将军家里教授孩子们德语和文学，这是一份高薪水的工作，使他在经济方面得以独立。福伊将军是拿破仑时代的战争英雄，1819年被选入众议院，担任反对派领袖。他的住所是巴黎许多名人的聚会场地，这使狄利克雷在社交方面获得自信并对他今后的生活产生了显著的影响。这份工作一直持续到1825年11月28日福伊因心脏病去世。福伊一家视他为家人，狄利克雷在这期间过得非常舒适。多年后，福伊的遗孀还记得那个身材瘦长的家教老师坐在狭窄的炉子边上，一边监督孩子们学习，一边继续自己的研究^[1]。

狄利克雷的家教工作结束后，当务之急便是寻找一份固定的工作。在傅里叶和泊松的建议下，狄利克雷开始接触洪堡（A. von Humboldt）。第一次拜访洪堡时，狄利克雷就表达了他想回普鲁士寻求职位的愿望，并得到了洪堡的支持和帮助。

亚历山大·冯·洪堡

1826年5月14日，狄利克雷在洪堡的帮助下，给洪堡的老朋友普鲁士文化和教育部长阿尔滕斯坦（F. von Altenstein）写了一封求职信，并附上他的研究成果和洪堡的推荐信。狄利克雷也将其研究成果的副本和对艾特魏因（A. Eytelwein）文章的译文以及洪堡的推荐信一起寄给了柏林科学院，希望得到艾特魏因院士和天文学家恩克（F. Encke）的支持，恩克是高斯的学生也是柏林科学院的干事。在1826年5月28日，狄利克雷又给高斯写了一封信，连同研究成果副本和洪堡的推荐信寄到了格丁根，信中狄利克雷说明了他的情况。^[2]

后来高斯写信给恩克，极力夸赞了狄利克雷表现出的卓越才能，这令恩克十分震惊，然后毫不犹豫地将此事告诉了教育和文化事务部的相关负责人。因为在恩克看来，高斯的这个评价有很高的价值，并且自从他认识高斯以来，从未见过高斯以如此热情的方式表达意见。恩克告诉高斯事情的进展之后，高斯在1826年给狄利克雷写了一封信，亲切地告诉他事情的进展并表达了他对狄利克雷的美好祝愿。等待结果期间狄利克雷回到了迪伦。

他的申请获得了回应，阿尔滕斯坦在布雷斯劳大学给狄利克雷提供了一个教师职位。由于狄利克雷还没有通过博士考试，在阿尔滕斯坦的帮助下，波恩大学在1827年授予狄利克雷荣誉博士学位。同年春天狄利克雷从迪伦搬到布雷斯劳任职，这期间狄利克雷曾绕道格丁根亲自拜访高斯。

到布雷斯劳后，狄利克雷先是获得了任职资格。1827年4月1日，他正式成为布雷斯劳大学的一名讲师，年薪400泰勒，1828年升为副教授^[1]。

后来狄利克雷有了去柏林工作的机会。又一次在洪堡的帮助下，狄利克雷得到了柏林军事学院的一个职位。因为阿尔滕斯坦允许狄利克雷在休假期间到军事学院任教，所以狄利克雷先是在布雷斯劳申请了10个月的带薪假期。1828年10月1日，狄利克雷开始在军事学院任职，年薪600泰勒。刚开始是做助教，一年后才正式教学。后来狄利克雷又延长了两次假期，后来再也没有回到过布雷斯劳。

当然，军事学院并不是吸引他的地方，吸引他的是能够同时在柏林大学任教^[3]。1828年，狄利克雷开始在柏林大学教书，1831年正式调到柏林大学哲学系，提升为副教授，同时也保留了在军事学院的工作，这使得狄利克雷的工作比他所希望的繁重很多。同年，狄利克雷入选柏林皇家科学院，经国王确认后，选举于1832年生效。当时27岁的狄利克雷是科学院中最年轻的成员。1839年，狄利克雷被提升为柏林大学正教授。

就这样，狄利克雷在军事学院和柏林大学一直工作到1855年。其实狄利克雷本可以继续在柏林大学任职，不过他却有了离开军事学院的想法，主要有两方面原因。其一是，多年来狄利克雷厌倦了军事学院每三年就重复的课程，加上他在柏林大学的课程，每周的教学工作量通常是18个小时左右，很繁重，令他没有足够的时间进行研究。其二是，1848年三月革命之后，当军事学院重新开放时，狄利克雷的自由主义信念和军官们的精神截然相反。这两个原因致使他想从军事学院辞职的愿望越来越强烈。但经济条件不容许他干脆利落地直接辞职，他需要一笔补偿以弥补他的收入损失，因为他在柏林大学的薪水相当微薄。1855年，高斯去世，格丁根大学向狄利克雷发出邀请，希望他能继任高斯的工作。狄利克雷当时并没有立即答应，而是利用它向普鲁士文化部提出请求，希望能辞去军事学院的职位并获得补偿，但并没有得到及时的答复，当普鲁士政府极不情愿地答应他的请求时，狄利克雷已经决定应邀前往格丁根。此后狄利克雷再也没有换过工作，直到去世。政府的态度仿佛是压死骆驼的最后一根稻草，让狄利克雷最终下定决心离开柏林，即便他依然喜欢柏林大学的工作。

狄利克雷1825年结束学业，耗时一年用来落实工作，1827年步入了教育行业，那一年他才22岁，而且终身从教。工作期间，狄利克雷因学识渊博而受尊敬，因谦虚而受欢迎。他的一生不仅影响和培养了一大批优秀的数学家，还提升了德国数学和教学水平。

在军事学院任教期间，狄利克雷开设的课程有方程论、级数论、体积测量、画法几何、三角学、二次曲线理论、解析几何、微分和积分、分析力学、流体力学、大地测量学等。起初微分和积分并不包括在课程内，狄利克雷通过把所谓的高等分析及其在力学问题上的应用引入课程，成功提高了教学水平。这也标志着一些微积分第一次被引入课程。

在柏林大学的最初几年里，狄利克雷的学生很少，一般是5到10人。有些讲座甚至因为学生太少而无法进行。但这并不奇怪，因为绝大多数学生只满足于通过期末考试，而狄利克雷课程的要求远不止于此。但很快，随着学生们数学水平的提升，再加上狄利克雷明智地选择了更适合的授课内容，增加了和学生们相处的时间，狄利克雷优秀教师的名声广为人知，学生也增加到了20到40人，这在当时是相当多的。

狄利克雷是德国第一个讲授数论以及分析技术在数论中的应用的大学教师，这也是他最喜欢的科目，他的讲座有23次是关于这些主题的。最重要的是，雅可比（C. Jacobi）在哥尼斯堡的讲座和狄利克雷在柏林的讲座推动了德国数学教学水平的普遍提高，从19世纪下半叶到1933年，德国大学数学基本上都达到了很高的水平。^[2] 

 
雅可比 

在那个时代，很多人都受到了狄利克雷的影响，或是通过他的讲座，或是通过和他交谈。无须细说他是如何影响的，只这一长串的名字就足以令人震惊。他们是巴赫曼（P. Bachmann）、鲍尔（G. Bauer）、博尔夏特（C. Borchardt）、康托尔（M. Cantor）、克里斯托费尔（E. Christoffel）、戴德金（R. Dedekind）、艾森斯坦（G. Eisenstein）、恩尼珀（A. Enneper）、海涅（E. Heine）、克罗内克（L. Kronecker）、库默尔(E. Kummer)、利普希茨（R. Lipschitz）、黎曼、舍林（E. Schering）、施罗特（H. Schröter）、赛德尔（P. Seidel）、魏因加滕（J. Weingarten）、戈佩尔（A. Goepel）、福尔辛（J. Foelsing）、穆勒（E. Müller）、格哈特（C. Gerhardt）、米凯利斯（G. Michaelis）和博伊曼（J. Boymann），其中大多数人后来都成为著名数学家，也有一部分是中学老师。除此之外，许多化学和物理专业的学生也听过狄利克雷的讲座，比如巴伦丁（F. Barentin）和维德曼（G. Wiedemann），他们是著名物理学家马格努斯（G. Magnus）和化学家米切尔利希（E. Mitscherlich）的学生。

狄利克雷的辉煌成就主要体现在数学和力学两方面。和很多著名数学家相比，狄利克雷发表文章不算多，但文章质量非常高。高斯曾评价道：“狄利克雷的作品是珠宝，珠宝不能用杂货店的秤来衡量。”^[5]

狄利克雷的第一部作品是对柏林皇家科学院成员艾特魏因关于流体动力学的一篇论文的法文翻译稿，它为狄利克雷赢得了赞誉。1825年，狄利克雷完成了他的第一篇数学论文“关于某些五次不定方程的不可解”，在文中狄利克雷讨论了费马大定理n=5的情况。狄利克雷向法国科学院提交这篇论文后获得给科学院成员进行讲座的许可。这次讲座在当时很轰动，狄利克雷也因此赢得了科学界的高度认可，因为他那时还只是一个默默无名的20岁德国学生。7年后，也就是1832年，狄利克雷又证明了n=14情况下的费马大定理。这次讲座也使狄利克雷与许多著名院士有了更密切的联系，特别是傅里叶和泊松，他们唤醒了狄利克雷对数学物理的兴趣。与傅里叶的熟悉以及对其热分析理论的研究为狄利克雷后来进行关于傅里叶级数的划时代研究做了铺垫。

由于高斯，狄利克雷对双二次剩余这个主题产生了兴趣。1825年4月，高斯首次发表了他关于双二次剩余的论文。我们知道，整数a是模p的双二次剩余，其中p为奇素数且p|a，当且仅当同余式x⁴≡a(mod p)有整数解。在这篇文章的最后高斯谈到了关于数±2的双二次特征的结果，这使狄利克雷对该主题产生了浓厚兴趣，后来狄利克雷不仅发现了这个结果的简单证明，还得出许多新的结果。自此双二次剩余这个主题一直留在狄利克雷的脑海中，直到他生命结束。

高斯

狄利克雷1829—1830年间的作品讨论的主题主要是分析问题。这期间狄利克雷对收敛理论做出了重大贡献，即在处理傅里叶级数和区分绝对收敛和条件收敛方面。实轴上“任意”以2π为周期的函数能否展开成三角级数（现称傅里叶级数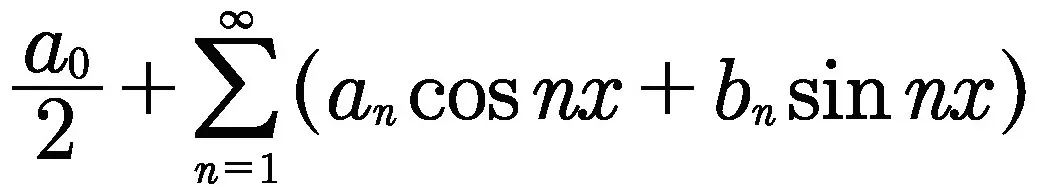），是18世纪伟大分析家们争论不休的话题，狄利克雷是第一个给出严谨证明的数学家，他在其1829年的论文“关于用于表示给定极限之间任意函数的三角级数的收敛性”中，讨论了任意函数展开成傅里叶级数及其收敛性。

狄利克雷工作的一个典型特点是用分析方法解决数论问题，他也因此成为解析数论的创始人。这一特点首次出现在其1835年的论文“关于定积分在有穷或无穷级数求和中的新应用”中。1837年，狄利克雷首次给出了算术级数中素数分布的证明，即任何首项与公差互素的算术级数中存在无穷多个素数，其中首项和公差为正整数，这可以说是他将分析应用于数论最令人印象深刻的体现。狄利克雷能够证明这一定理的关键的新工具是L级数，现以狄利克雷的名字命名。在发表这篇论文后不久，狄利克雷又分别于1838年和1839年发表了两篇关于解析数论的更深刻的论文。这些论文介绍了狄利克雷级数，确定了关于二次型的类数公式。1840年，狄利克雷在论文“关于二次型的性质”（Uber eine Eigenschaft der quadratischen Formen）中又将算术级数中素数分布的定理推广到了形如ax²+2bxy+cy²的二次型，其中a, 2b, c没有公因子。

1834年狄利克雷提出了一个简单而高效的原理——抽屉原理，即若将多于n个的物体放入n个抽屉，则至少有一个抽屉中有不止一个物体。后来人们也将其称之为鸽笼原理，该原理在现代数论中具有重要作用。1842年狄利克雷在论文“连分数理论中一个定理的推广及其在数论中的一些应用”中呈现了鸽笼原理的惊人应用。进一步地，鸽笼原理在狄利克雷后来证明单位定理时也发挥了重要作用。

1837年，狄利克雷提出了函数的现代定义，即如果变量y与变量x相关，使得根据某个规则，每个x值都对应唯一一个y值，那么y就是关于自变量x的函数。

从1840年开始，狄利克雷将由整系数方程xⁿ+ax^n-1+bx^n-2+…+p=0定义的量（所谓的代数整数）置于他研究的中心位置^[6]，发表了一系列相关论文，并在1846年给出并证明了一般情形的单位定理，后来这一定理逐步演变为著名的“狄利克雷单位定理”。不得不说的是，狄利克雷的类数公式和单位定理是建立代数数论的重要支柱，在代数数论的发展中占据重要地位。

《数论讲义》也是狄利克雷极其重要的贡献，这本书是由戴德金^[7]根据狄利克雷的讲座编辑出版的，是对高斯《算术研究》最好的诠释，其中也包含了不少狄利克雷自己的创见，是数论经典著作之一。

《数论讲义》

在力学方面，狄利克雷研究了系统的平衡和位势论。这些研究始于1839年发表的几篇论文，给出了多重积分的估值方法，并将其应用于确定椭球体对其内部或外部任意质点的引力。之后狄利克雷转向拉普拉斯证明太阳系稳定性的问题，这使他得到了关于给定边界条件下的调和函数的狄利克雷问题（也称第一边值问题）。1852年，狄利克雷研究了球在不可压缩流体中的运动问题，在这一研究过程中，他成为第一个精确解出流体力学方程的人。^[3]

狄利克雷的主要论文收录在《狄利克雷全集》（G. Lejeune Dirichlet's Werke）中，共两卷，第一卷由克罗内克编辑，出版于1889年，第二卷由富克斯（L. Fuchs）完成，并于1897年出版。

科赫（H. Koch）曾这样评价狄利克雷的贡献：数学的重要部分都受到狄利克雷的影响。他证明的惯常思路是从令人惊讶的简单观察开始，然后对剩下的问题进行极其敏锐的分析。随着狄利克雷的到来，柏林迎来了数学的黄金时代。^[3]

搬到柏林后，通过洪堡引荐，狄利克雷结识了亚伯拉罕·门德尔松·巴托尔迪（Abraham Mendelssohn Bartholdy）一家。亚伯拉罕是一位成功的银行家，其父亲是鼎鼎有名的哲学家摩西·门德尔松（Moses Mendelssohn）。亚伯拉罕还有4个优秀子女，分别是芬妮（Fanny）、费利克斯（Felix）、丽贝卡（Rebecca）和保罗（Paul）^[10]，其中芬妮和费利克斯都是著名钢琴家和作曲家，保罗是著名大提琴家和演奏家，丽贝卡虽然没有那样的音乐天赋，但她机敏、博览群书、魅力十足。^[1]

丽贝卡·门德尔松

门德尔松一家习惯定期举办宴会——著名的周末音乐会，就在他们家的大花园中。这也是柏林文化的一个独特聚会地，很多名人都会参加。聚会上兄弟姐妹四人会进行表演，人们也会谈论各种话题，比如政治、科学、音乐、艺术、历史、哲学等。结识亚伯拉罕后，狄利克雷也加入了这个社交圈。得益于此，狄利克雷和丽贝卡相遇、相识、相知。

狄利克雷一开始就喜欢上了丽贝卡，虽然丽贝卡追求者众多，但她还是选择了狄利克雷。他们在1831年11月订婚，1832年5月结婚。从此，丽贝卡深深影响其一生，狄利克雷和音乐也愈发紧密。

顺便提一下，在1832年，狄利克雷的生活本可以走上完全不同的道路。高斯原本计划推荐狄利克雷作为他已故同事——数学家蒂鲍特(B. Thibaut)的继任者，但当他听说狄利克雷已经结婚的消息后就打消了这个念头，因为他认为狄利克雷不会愿意离开柏林。

1833年7月2日，狄利克雷和丽贝卡迎来了他们的第一个孩子——沃尔特（Walter），后来他成为一位著名的政治家，并于1881—1887年成为德国国会的议员。

关于沃尔特的出生有一则趣事。狄利克雷是出了名的懒于写信，这一点和他的父亲很像，他更喜欢通过直接联系来解决问题。亚伯拉罕在伦敦的一次商业旅行中得到了沃尔特出生的消息，他在信中向丽贝卡表示祝贺，并愤愤不平地继续说：“我不祝贺狄利克雷，至少不在信中祝贺他，因为即使在这种情况下，他也不肯给我写一个字；至少他可以这样写：2+1=3。”^[2]

之后狄利克雷夫妇又有了三个孩子，分别是费利克斯（Felix）、恩斯特（Ernst）和女儿弗洛拉（Flora），不幸的是费利克斯在1岁的时候就去世了。

1843年，狄利克雷一家开始了意大利之旅。1843年初，狄利克雷的好朋友雅可比被诊断出患有糖尿病，医生建议他去气候温和的意大利疗养。后来狄利克雷也申请了18个月的假期，并于1843年秋季和雅可比一起动身前往意大利。与他们同行的还有施泰纳（J. Steiner）、雅可比的学生博尔夏特以及精通意大利语等多种语言的施莱弗利（L. Schläfli）。他们的女儿弗洛拉就是在这次旅行期间出生的。值得一提的是，意大利旅行期间，狄利克雷在西斯廷教堂听复活节音乐时突发灵感，发现了一般情形单位定理的证明思路。

1855年，狄利克雷一家搬到格丁根。格丁根的生活是舒适的，这里没有繁重的工作。下课后，狄利克雷会抽出时间在家里与丽贝卡和他妈妈一起喝茶，这是在柏林没有的，因为那里家和教室距离太远。格丁根的许多教师是业余音乐家，狄利克雷夫妇也经常听音乐，丽贝卡深受音乐爱好者的喜爱，不仅是因为她兄弟姐妹名字的光环，还因为她支持音乐活动，丽贝卡也会在家中举办音乐会。^[2]狄利克雷很满足，他在这里度过了一段轻松快乐的时光。特别是，她在格丁根大学协助狄利克雷和黎曼形成良好的音乐氛围，是格丁根大学历史上温馨浪漫的一笔^[9]。

然而，幸运之神并不是一直都在。1858年夏季学期结束后，狄利克雷去瑞士蒙特勒旅行。在蒙特勒，狄利克雷心脏病发作，回到格丁根时已是病危。通过精心照料，他似乎康复了。然而，谁都无法预料意外和明天哪个先到，同年11月29日，丽贝卡中风了，之后她一直处于昏迷状态，直到12月1日早上去世。丽贝卡的突然离世对狄利克雷的打击很大，使他的病情愈加严重，此后的五个月，他基本上卧床不起，似乎对生活失去了希望。这可能是狄利克雷一生中最痛苦的日子了，痛苦到不想去克服，悲伤到任由病魔肆虐侵蚀，最终，在1859年5月5日，狄利克雷与世长辞，享年54岁。

人的一生，或多或少，或大或小，总会遇到一些挫折，经历一些磨难。狄利克雷的一生是机遇和磨难相伴的一生，有喜悦也有悲伤，有挫折亦有幸运。纵观狄利克雷一生，是成功的、幸福的、辉煌的，是令人敬仰的。

[1]Merzbach Uta C. Dirichlet. Cham: Birkhäuser, 2018: 1-276.

[2]William D, Tschinkel Y. Analytic Number Theory—A Tribute to Gauss and Dirichlet. Providence: American Mathematical Society/ Cambridge: Clay Mathematics Institute, 2005: 1-38.

[3]O'Connor J J, Robertson E F. Johann Peter Gustav Lejeune Dirichlet. https://mathshistory.st-andrews.ac.uk/Biographies/ Dirichlet/

[4]李晓奇. 先驱者的足迹: 高等数学的形成. 沈阳: 东北大学出版社, 2004: 227-231.

[5]Gorkin P, Smith J H. Dirichlet: His Life, His Principle, and His Problem. Mathematics Magazine, 2005, 78(4): 283-296.

[6]Klein F. Development of Mathematics in the 19th Century. Brookline: Math Sci Press, 1979: 87-90.

[7]王淑红, 孙小淳. 心灵的创造：戴德金的数学思想. 自然辩证法通讯, 2019, 41(2): 115-122.

[8]Archibald R C. Mathematicians and Music. The American Mathematical Monthly, 1924, 31(1): 1-25.

[9]蒋迅, 王淑红. 数学都知道1. 北京: 北京师范大学出版社, 2016: 81-82.

[10]苏洋, 王淑红. 库尔特·亨泽尔的数学人生. 今日科苑, 2021, (8): 54-63.