编者按
玻色出生于1894年1月1日，是20世纪物理学最杰出的人物之一。这篇文章由玻色以前的学生Partha Ghose教授撰写，旨在向一位量子领域开拓者的一生致敬——他与爱因斯坦一起确立了量子力学的新方向。可以预见，他的名字将一直在科学发现的史册上回响。今年正值玻色诞辰130周年，也是玻色—爱因斯坦统计提出100周年，特刊登此文，以飨读者。
撰文 | Patha Ghose
翻译 | 1/137
玻色（Satyendra Nath Bose，1894.1.1-1974.2.4）
萨延德拉·纳特·玻色（Satyendra Nath Bose）有着一头浓密显眼的白发，一双大眼睛极具穿透力，脸上常常挂着灿烂的笑容，对科学、文学和艺术有着浓厚的兴趣，他的名字与爱因斯坦联系在一起——在其有生之年，他是一个传奇人物。1924年，他在达卡写了一篇精彩的论文，证实了爱因斯坦关于光子的有争议的观点[1]。达卡是孟加拉国的首都，但在科学的世界里它实际上岌岌无名。这篇论文表明光子不是普通的粒子，而是奇怪的实体，它们倾向于按照一种不同的粒子统计规律聚集在一起。爱因斯坦读了这篇论文，他对自己的想法得到出乎意料的支持而感到振奋，于是将玻色的方法应用于理想气体，奠定了气体的量子理论的基础。这种新的统计学被称为玻色—爱因斯坦统计（Bose–Einstein statistics）。事实上，玻色并没有意识到他的观察结果是真正独创性的。[2]物理学家、爱因斯坦的传记作者派斯（Abraham Pais）指出，“自从普朗克在1900年引入量子以来，还没有出现过如此成功的猜测（shot in the dark）。”[3]玻色的论文是完成旧量子论并导致新量子力学的四篇革命性论文中的最后一篇，其他三篇分别是1900年普朗克、1905年爱因斯坦和1913年玻尔的论文[4]。
玻色于1894年1月1日出生在英属印度的首都加尔各答。这里被视为大英帝国继伦敦之后第二个日不落之城。当时，正值孟加拉文艺复兴运动，民族自豪感的觉醒是显而易见的，该运动始于18世纪后期，由拉贾·拉姆·莫汉·罗伊（Raja Ram Mohan Roy）带头。一群才华横溢而叛逆的人登上历史舞台，从本质上讲，他们从印度的立场接受西方的知识和科学。玻色的家族也参与了这一运动，他的父亲苏伦德拉纳特（Surendranath）受到启发，建立了自己的化学和制药工业。它很快引发了随之而来的政治运动。这场动乱让英国人感到不安。1905年，当玻色只有11岁的时候，英国总督柯曾勋爵（Lord Curzon）把孟加拉一分为二。这一分治引发了广泛的抗议，触动了许多年轻人的生活。玻色的父亲教导他唯一的儿子不要参与政治运动，也不要参加任何音乐活动。他服从了第一个命令，但暗中没遵守第二个。
玻色的数学才能在他上高年级时开始显露出来。他的数学老师曾经在一次满分为100分的课堂测验中给了他110分。他正确地回答了所有问题，在某些题目上，他演示了不止一种得到答案的方法。这位老师预言玻色有一天会成为伟大的数学家。
玻色随后进入著名的总统学院（Presidency College），在那里教他的教授包括物理学家兼植物学家贾格迪什·玻色（Jagadish Chandra Bose），他是微波的发现者和植物电生理学的先驱；化学家普拉富拉·雷（Prafulla Chandra Ray），他以对亚硝酸汞的研究，以及作为一位伟大的教师、历史学家、实业家和慈善家而闻名。玻色的同学中有梅格纳德·萨哈（Meghnad Saha），他来自东孟加拉邦（现在的孟加拉国）的一个贫困家庭，后来在天体物理学方面做了开创性工作。萨哈是第一个应用玻尔原子理论，根据恒星表面附近原子的电离程度来计算恒星的温度、压强和化学成分的人。这项工作解释了为什么恒星似乎具有完全不同的化学成分，具体取决于它们的大小和温度。
玻色和萨哈成为了好朋友。他们一起学习数学，最终都被任命为加尔各答大学新成立的科技学院的物理学助理讲师，该学院成立于1914年。两人一起学习了德语、法语和英语，以便能够研究普朗克、爱因斯坦和其他欧洲科学家撰写的论文。
1919年5月29日的日全食之后，物理学界发生了一个重大事件，即爱丁顿（Arthur Eddington）观察到星光在太阳附近发生了偏转。他的观察结果证实了爱因斯坦对光的引力弯曲的预测。这之后，玻色和萨哈将爱因斯坦和闵可夫斯基（Hermann Minkowski）的所有论文从德语翻译成英语。加尔各答大学于1920年出版了一本名为《相对论原理》（The Principle of Relativity）的书，并由玻色和萨哈的朋友马哈拉诺比（Prasanta Chandra Mahalanobis）做了历史回顾，他后来成为印度统计学的先驱。这是爱因斯坦论文的首个英译本。
玻色和萨哈合作撰写了他们的第一篇关于真实气体状态方程的研究论文。[5]萨哈随后出国，在英国与福勒（Ralph Fowler）一起工作，在那里他进一步发展了他的热电离理论（theory of thermal ionization）。玻色则加入了新成立的达卡大学，担任物理学高级讲师（Reader in Physics）。在达卡教授量子理论时，他首先注意到普朗克黑体辐射定律的所有已知推导中存在的逻辑问题（编者注：参见《黑体辐射公式的多种推导及其在近代物理构建中的意义(四) 》）。当萨哈提请他注意泡利（Wolfgang Pauli）刚刚发表的关于黑体辐射定律的推导时，这个问题进一步凸显[6]。泡利提出了一个猜测性的电子—光子散射概率，它取决于始态和末态，这在当时看起来很疯狂。在1923年底到1924年初的某个时候，玻色在努力解决这个问题，然后突然想到了属于他的伟大想法。通过使用新的统计，他将黑体辐射视为光子气，从而成功地导出了普朗克公式，而没有之前那种逻辑上的困难。由于无法在《哲学杂志》（Philosophical Magazine）上发表，他把论文寄给了爱因斯坦，并谦恭地请求将其译成德语并发表在一家声誉卓著的德国期刊上。当然，爱因斯坦对他的光子思想得到意外证实感到高兴，尽管玻色为得出正确的统计而对其进行了调整。爱因斯坦亲自翻译了这篇论文，并在Zeitschrift für Physik上发表，还附上译者按：“在我看来，玻色的推导标志着一个重要的进展。这里使用的方法给出了理想气体的量子理论，我将另行解决。”[7]
爱因斯坦关于新的统计的开创性工作就这样开始了。在1924年7月10日、1925年1月8日和1925年1月29日与柏林普鲁士科学院（Prussian Academy）的通信中，他将玻色的方法推广到理想气体，并预言了玻色—爱因斯坦凝聚体（Bose–Einstein condensates），这是一种直到70年后才被观察到的超冷物质形态。[8]
这一发现值得更详细地介绍。
玻色统计的故事
1900年10月7日，星期日下午，鲁本斯（Heinrich Rubens）与普朗克一起喝茶，并告诉后者他和库尔鲍姆（Ferdinand Kurlbaum）获得的黑体谱的最新实验数据。鲁本斯离开后，普朗克开始寻找一个能够拟合黑体谱数据的数学公式。他的公式成功了，
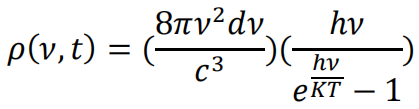
纳入了新的带有作用量量纲的基本常数h。它与经典的瑞利—金斯定律（Rayleigh–Jeans law）和经验建立的维恩定律（Wien’s law）一致，但仅限于低频和高频极限，而中间区域则不符。很明显，能准确拟合整个频谱数据的插值公式无法从经典理论中推导出来。这显然需要一些理论上的理由。普朗克非常努力地尝试，最后，作为“绝望的行为......无论如何，不惜一切代价获得预期的结果”，他为腔壁上的作用，而不是辐射本身，引入了能量不可约化波包（irreducible packet），或者说量子（quanta）的概念[9]。1900年12月中旬，他提出了一个统计推导，涉及假设的腔壁振子中能量量子的分布W。它没有更多的理由，只是给出了预期的结果。1907年，他写道：
我不是在寻求真空中作用量量子[光量子]的意义，而是在发生吸收和发射的地方，[我]假设真空中发生的事情可以用麦克斯韦方程组严格描述。[10]
爱因斯坦于1905年登上舞台。凭借他在热力学和统计力学方面的背景，并考虑到玻尔兹曼的熵的方程 S = k lnW，他意识到普朗克推导其定律的基础并不稳固。他怀疑该定律暗示了辐射本身的非经典的、微粒性的性质，于是他使用维恩（Wilhelm Wien）关于辐射熵的结果来计算热辐射熵的体积依赖性。爱因斯坦得出了革命性的结论，即低密度的单色（monochromatic）辐射（在维恩辐射公式的有效范围内）在热力学上表现得好像它由大小为Rßν / N等份的相互独立的能量量子组成。[11]因子Rßν/ N等于hν。于是光量子的概念诞生了，现在称为光子。爱因斯坦将这一原理应用于三个经验上已知的现象：光致发光（photoluminescence）中的斯托克斯定律（Stokes rule）、光电效应（photoelectric effect）和紫外线对气体的电离。其中，对光电效应的应用引起了公众最多的关注，因为它最终使爱因斯坦获得了诺贝尔奖。
但爱因斯坦关于相互独立的能量量子的想法有其自身的问题。纳坦森（Władysław Natanson），以及埃伦费斯特（Paul Ehrenfest）和昂内斯（Heike Kamerlingh Onnes）表明，它与普朗克定律相冲突，因此与普朗克分布W相冲突，后者需要不可区分和关联的（indistinguishable and correlated）量子，而不是相互独立的量子。[12]
大多数物理学家对光量子假说持怀疑态度，即使在密立根（Robert Millikan）对光电效应进行了细致的研究工作，验证了爱因斯坦的简单的方程之后。密立根本人在他1916年的论文中评论说：“然而，爱因斯坦得出这个方程式的半微粒理论目前似乎是完全站不住脚的。”[13]主要问题是如何用光量子来解释确立已久的辐射的波动特性。这种偏见是如此强烈，以至于即使是热衷于将爱因斯坦带到柏林的普朗克、鲁本斯、能斯特（Walther Nernst）和瓦尔伯格（Emil Warburg）也不得不写信给普鲁士教育部：
他的推测可能有时偏离了目标，例如在他的光量子理论中，这并不是他的缺点。因为在最精确的自然科学中，每一项创新都伴随着风险。[14]
玻尔也反对光量子的想法，并在他1913年关于原子模型的论文中避免使用这一术语[15]。紧随普朗克之后，他引入了原子定态之间的跃迁，从而产生经典辐射的吸收或发射，其频率由关系ν=(E1-E2)/h决定。与教科书中通常所说的相反，他根本没有提到光量子。
最终在1923年，康普顿效应（Compton effect）给出了支持光量子的强有力的实验证据。经典的辐射波动理论无法解释观察到的被散射的X射线波长的变化。观测清楚地指出了光量子和原子中电子之间能量转移的基本过程。
尽管支持光量子假说的经验证据越来越多，但其理论基础在三个方面仍然不令人满意。首先，爱因斯坦光量子的统计独立性与普朗克定律之间存在根本冲突。其次，即使包括普朗克本人以及爱因斯坦、埃伦费斯特、泡利和德拜（Peter Debye）在内的著名物理学家进行了多次尝试，但普朗克定律在逻辑上并没有令人满意的推导。[16]所有这些尝试虽然巧妙，但都有一个缺点。在所有推导中，普朗克定律的第一个因子，8πν2dν/c3，总是按经典电动力学取为单位体积内的辐射振动模数。这些作者通过为不同的基本过程假设特定（ad hoc）规则，以不同的方式导出第二个因子。第三，除了德拜的之外，所有这些尝试都使用了普朗克的假设，即量子化仅限于辐射和物质之间的能量交换，但康普顿效应表明辐射本身由能量量子组成。
1924年，玻色从量子理论中推导出包括第一因子的完整的普朗克定律，一举解决了所有这些问题。他通过将普朗克的物质振子量子化方法推广到辐射本身，从而实现了这一目标。除了一个2倍的因子之外，第一个因子最终表现为光子相空间中不可约相格的数量——即光子的量子态数，因此也是光子的可能排列数。所以，光子的量子态仅通过每种态中的光子数来区分。这一事实直接意味着光子，不仅仅是腔壁内假设的振子，而且是无法区分的。整个物理学由此变得通透。
1924年6月4日，玻色致信爱因斯坦：
我斗胆将我的论文寄给您，希望您能审阅并给出意见。我非常急切地想知道您对论文的看法。您会看到，我在没有使用经典电动力学的情况下推导出普朗克定律中的系数，仅假设相空间应该被分成很多小格，每格大小是h3 [17]。【译者注：玻色原始信件中紧接着表达了请求爱因斯坦帮助发表它的愿望，“我的德文不够好，无法将论文翻译成德文。如果您觉得这个文章值得发表，请您帮忙安排它在Zeitschrift für Physik发表。尽管对您来说，我是一个完全的陌生人，我还是毫不犹豫地向您致以请求。因为我们都是您的学生，尽管只能通过阅读您的论文而聆听教诲。”】
原文: I have ventured to send you the accompanying article for your perusal and opinion. I am anxious to know what you think of it. You will see that I have tried to deduce the coefficient () in Planck’s law independent of the classical electrodynamics, only assuming that the ultimate elementary regions in Phase space have the content h3.
爱因斯坦在同年7月12日致埃伦费斯特（P. Ehrenfest）的信中写道：“印度人玻色给出了包含常数8πν2/c3的普朗克定律一个漂亮的推导。”[18]
不过，由于光的两种偏振态并不完全是量子力学的，他对第一个因子的推导必须辅以因子2。爱因斯坦在7月2日给玻色的明信片中写到：
亲爱的同行，
我已经翻译了您的论文，并将其传达给Zeitschrift für Physik杂志发表。这标志着向前迈出了重要的一步，我非常喜欢它。事实上，我认为你对我的工作的反对是不正确的。因为维恩位移定律没有假设波动的（涨落）理论，并且玻尔的对应原理（correspondence principle）是完全不适用的。然而，这无关紧要。你是第一个从量子理论上推导出该因子的人，即便偏振因子2并不是完全严格的。这是向前迈出的漂亮一步。
此致
问候，
您的，
爱因斯坦[19]
在这次信件往来的多年以后，我同玻色就他推导中的因子2进行了交流。一天下午我去见他，发现他在沉思。他回忆起1925年在柏林与爱因斯坦的会面和谈话。突然他对我说，他想告诉我一件机密的事，我绝对不能透露给任何人。他起身关上门窗。我满腹狐疑。他坐下来给我讲了下面的故事。
“你知道，”他说，“我对普朗克定律的推导缺个因子2。所以我提出，它来自光子有自旋的事实，光子自旋可以与运动方向平行或反平行。这就得到了额外的因子2。但是老先生（指爱因斯坦）把它划掉了，说没有必要讨论自旋，因子2来自于光的两种偏振态。”
然后他调皮地笑了笑，用婉转的口吻对我说：“我能理解旋转的粒子，但粒子的偏振是什么意思呢？”
我十分震惊！立即对他说：
“先生，当光子自旋最终被发现时，你为什么不告诉爱因斯坦你早在1924年就发现了？毫无疑问，像爱因斯坦这样的人会支持你，你肯定会获得诺贝尔奖！ ”
他平静地看着我说：“谁发现它有什么关系？”然后带着一种胜利的喜悦说道：“总之它被发现了，不是吗！”
这就是玻色。
很久以后，大约是1993年，我们在为玻色百年诞辰纪念做准备，当我在印度科学培养协会（Indian Association for the Cultivation of Science）图书馆浏览过刊时，偶然发现了拉曼（Chandrasekhara Venkata Raman）和巴伽万塔（Suri Bhagavantam）1931年在《印度物理学杂志》（Indian Journal of Physics）上发表的一篇论文，题目是《光子自旋的实验证明》（Experimental Proof of the Spin of the Photon）。我很感兴趣，于是读了起来。我立即被里面的内容惊呆了:
在他著名的从量子统计推导普朗克辐射公式的过程中，玻色教授得到了辐射在相空间中占据的单元（相）格数的表达式，并且他发现必须将其乘以一个数值因子2，才能从中得出单位体积中量子可能排列的正确数量。公开发表的论文并没有详细讨论引入这一因子的必要性，但我们和他的私人通信中了解到，他曾设想量子除了具有能量hν和线性动量hν/c之外，还具有围绕平行于其运动方向的轴的内禀自旋（intrinsic spin）或角动量±h/2π的可能性。因此，权重因子2产生于量子自旋为右旋或左旋的可能性，对应于角动量的两个可选符号。这一观点与著名的经典电动力学结果有着根本的区别。经典电动力学中，众所周知的结果是由[约翰·亨利]·坡印廷（John Henry Poynting）得出，并由[马克斯]·亚伯拉罕（Max Abraham）更充分地发展，即光束在特定情况下可能具有角动量……因此，根据经典场论，与能量量子相关的角动量并不是唯一定义的，而根据我们在本文中所关注的观点，光子的角动量总是具有一个玻尔单位的确定数值，取两个可能的互不相容的符号中的一个或另一个。[20]
【译者注：目前一般认为，关于光子“自旋因子2”的严格证明基于构建庞加莱群的幺正表示，细节请参见S. 温伯格《量子场论》卷一第五章。物理直观的简单解释：对于无质量粒子（如光子），纵向极化是不可能的。】
他们的实验最终决定性地证明了玻色的观点是正确的，并提供了光子自旋的第一个实验测量。科学家和科学史家几乎并不知道这个事实。
我欣喜若狂！但与此同时，我也对玻色吐露这一故事的讳莫如深感到困惑。毕竟，拉曼早在1931年就已经发表了它。难道玻色忘记了拉曼的论文吗？当然不可能——谁会忘记为自己的革命性思想作这样引人注目的证明呢？并且玻色具有惊人的记忆力。是拉曼没有告诉玻色他的结果吗？这似乎也不太可能。无论如何，从那时起，我打破了不泄露这个故事的承诺。我并没有感到内疚，对于科学史来说，广为人知是很重要的。
顺便说，我曾很努力地想弄到一份玻色寄给爱因斯坦的英文原版论文的副本。我想确证一下因子2那里到底是怎么写的。爱因斯坦档案（Einstein archives）中无此论文，尽管说明信（cover letter）和爱因斯坦提到这个谜题的回复都在。而玻色本人也从来没有留过一份副本。
尽管如此，当时很难预见到，一篇只有四页左右，没有任何参考文献的短论文，最终会在广泛的物理学领域产生深远的影响。
粒子物理中的玻色子
玻色论文发表后的首批影响之一是，英国物理学家狄拉克（Paul Dirac）创造了玻色子（Boson）这个词，用来指代遵循玻色—爱因斯坦统计的量子粒子。除了玻色子，只有另一类量子粒子：费米子（Fermion），它是狄拉克独立于费米（Enrico Fermi）发现的。玻色子和费米子遵循两种类型的量子统计：分别是玻色—爱因斯坦统计和费米—狄拉克统计（Fermi–Dirac statistics）。由于量子统计的最初想法来自于玻色，狄拉克选择将遵循前者统计的粒子命名为玻色子；出于谦虚，他将另一种类型命名为费米子。这些名称第一次出现在狄拉克的经典专著《量子力学原理》（The Principles of Quantum Mechanics）中。[21]
事实证明玻色子的内禀自旋是nℏ, n = 0, 1, 2, …；费米子的自旋是(n+1/2) ℏ，这被称为自旋统计定理（spin-statistics theorem）。玻色子和费米子之间的一个关键区别是，任意数量的相同玻色子可以占据相同的量子态，而两个或两个以上相同的费米子不能占据相同的量子态。玻色子的抱团行为导致了玻色—爱因斯坦凝聚；而费米子的冷漠行为，通过泡利不相容原理表达出来（Pauli exclusion principle）——这就是我们不能用一个手指穿过另一个手指的原因，即物质的刚性。
宇宙的基本组成部分只能是玻色子和费米子。根据粒子物理学的标准模型，轻子（lepton）——包括电子、缪子（muon，μ）、陶子（tauon，τ）、中微子和它们的反粒子，以及夸克和它们的反粒子都是费米子。传递它们之间相互作用的场的量子激发都是玻色子，包括光子，它传递电磁相互作用；W±和Z传递弱相互作用，如放射性；还有胶子，它结合夸克形成强子（hadron），比如中子、质子和π介子（pion）。
标准模型还需要一种基本粒子来产生轻子的质量，否则轻子就会像光子一样没有质量，以光速飞走，原子便不可能在宇宙中形成。这个粒子就是自旋为0的玻色子。它以爱丁堡大学的彼得·希格斯（Peter Higgs）的名字命名，称为希格斯玻色子，尽管其他几位物理学家在1964年几乎与希格斯同时提出了这种粒子。欧洲核子研究中心（CERN）耗资数十亿美元的粒子加速器——大型强子对撞机（Large Hadron Collider）花了近半个世纪的时间才找到了它。
这个被大肆宣传的结果最终在2012年7月4日，由欧洲核子研究中心主任休尔（Rolf-Dieter Heuer）宣布。一大群观众聚集在希格斯和恩格勒特（François Englert）所在的大厅，很多人整晚都在排队，而他只是简单地对观众说：“我想我们找到了。”希格斯和恩格勒特因此共同获得了2013年诺贝尔奖。
宇宙学中的玻色子
希格斯玻色子是理解宇宙大爆炸中轻子质量如何产生的内在因素。1964年，阿诺·彭齐亚斯（Arno Penzias）和罗伯特·威尔逊（Robert Wilson）在普林斯顿贝尔实验室（Bell Labs）使用霍姆德尔·霍恩天线（Holmdel Horn Antenna）时，意外发现了宇宙微波背景辐射（cosmic microwave background radiation），这是支持大爆炸理论所暗示的早期热宇宙的有力证据，违背与之竞争的稳恒态（steady-state）理论。由于这一具有里程碑意义的发现，彭齐亚斯和威尔逊被授予1978年诺贝尔物理学奖。事实证明，根据1994年宇宙背景探测卫星（Cosmic Background Explorer satellite）上的远红外绝对分光光度计（Far Infrared Absolute Spectrophotometer）进行的精确观测，宇宙微波背景辐射具有纯普朗克光谱，表明它是2.7K温度下热平衡的黑体辐射。
正是19世纪最后几年实验测量的黑体辐射光谱，使普朗克在1900年发现了量子理论。正是这一普朗克谱让玻色在1924年发现了新的统计。
玻色—爱因斯坦凝聚体
起初，每个人都觉得这个新的统计很奇怪，除了爱因斯坦，他立刻明白了它的重要性。玻色计算辐射量子态的方法表明，给定频率的光子是无法区分的。这意味着光子不能被连续地跟踪，这暗示了一种弥散的类波（wavelike）特征。爱因斯坦马上意识到，这样一个基本特征不可能仅限于辐射，通常的物质也一定是这样。他计算了极小体积的玻色气体中粒子数密度的涨落。他发现有两项：一项来自物质的粒子性质，而另一项令人惊讶——暗示了物质的类波特性。他立刻想起曾见过一位名叫路易斯·德·布罗意（Louis de Broglie）的年轻法国学者撰写的博士论文，其中提出物质波的可能性与辐射的对偶性【译者注：原文为dual nature，传统上一般译为二象性】类似。爱因斯坦最初似乎对德·布罗意的想法持保留态度，但是现在，通过他自己基于玻色气体的计算，他意识到该气体的类波特性不仅仅是类比。[22]然后，他开始撰写一系列的论文，在这些论文中，他解释了玻色的计数方法及其对物质气体的含义。爱因斯坦使用物质波波长的公式λ=h/mv，描述了将德布罗意波与物质气体联系起来的重要性，并提出了分子束实验来测试物质的类波性质。他还得出结论，在低于临界点的极低温度下，所有粒子都将在没有任何吸引作用的情况下，仅凭借其统计特性，凝结在系统的基态上[23]。由于温度非常低，它们的波长会增大（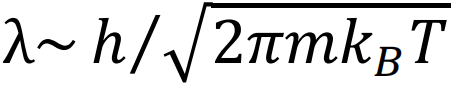
）。这些波长会相互重叠到一定程度，以至于它们会失去单独的“身份”，形成一个巨大的、与当时已知的任何东西都不同的类波实体——一种奇异的物质量子态，后来被称为玻色—爱因斯坦凝聚体。
直到70年后，人们才在实验室中制造出了玻色—爱因斯坦凝聚体。物理学家不得不等待极其精密的激光冷却（laser cooling）和蒸发冷却（evaporative cooling）技术的发展，才能制造出接近绝对零度的冷原子。最终，在1995年6月5日，科罗拉多大学博尔德分校的埃里克·康奈尔（Eric Cornell）和卡尔·维曼（Carl Wieman）在NIST-JILA实验室【译者注：美国标准局下属的JILA实验室】中制备出了第一个气态凝聚体。它是在冷却到170纳开【译者注：nanokelvin，1 nK=10-9K】的铷原子气体中产生的，仅仅比绝对零度稍高一点。稍后不久，沃尔夫冈·凯特勒（Wolfgang Ketterle）和他在MIT的团队在钠原子气体中也制备出了玻色—爱因斯坦凝聚体。这三位研究人员都因他们的发现获得了2001年诺贝尔物理学奖。根据诺贝尔委员会的说法，这三位科学家“使原子‘齐声歌唱’”。[24]
关于玻色—爱因斯坦凝聚体的最新论文【译者注：此处指截至本文的写作时间】发表在2020年6月的《自然》杂志上。它的题目是“在地球轨道研究实验室中对爱因斯坦凝聚体的观测”（Observation of Bose–Einstein Condensates in an Earth-Orbiting Research Lab）[25]。这项研究的目的是通过将大量原子置于微重力环境中来克服重力对它们的影响。这种情况可在自由落体的绕地卫星上实现。这延长了原子从“陷阱”中释放出来的自由落体时间，克服了地面上的限制。
超流和超导
尽管玻色—爱因斯坦凝聚在1995年才首次被直接观测到，但自发现超流动性和超导性以来，关于它们的间接证据就一直在积累。超流体是一种粘度为零的流体，它可以流过狭窄的管道而不损失任何动能。1938年，卡皮查（Pyotr Kapitsa）和艾伦（John Allen）发现了这一现象：当氦的两种同位素——氦-3和氦-4，被冷却到接近绝对零度时，它们发生液化，并显示出超流性。超流性可以产生各种奇异的物质状态，这些状态被认为发生在天体物理学、高能物理学和一些量子引力理论中。
超流性是玻色—爱因斯坦凝聚的一种表现。它发生在氦-4中，其原子具有整数自旋，因此是玻色子，可以在低于临界温度时凝聚。氦-3超流发生的温度比氦-4低得多，因为氦-3原子是费米子，必须有两个氦-3原子配对形成复合玻色子后才能产生凝聚。大卫·李（David Lee）、道格拉斯·奥舍罗夫（Douglas Osheroff）和罗伯特·理查森（Robert Richardson）因发现氦-3超流而获得1996年诺贝尔奖。2003年，安东尼·莱格特（Anthony Leggett）基于配对后的玻色子特性，提出了氦-3超流的量子力学理论，他也因此获得了诺贝尔奖。
某些物质在低于临界温度时发生超导现象。在此温度下，它们突然失去了所有的电阻，并排出磁通量，这就是所谓的迈斯纳效应（Meissner effect）。正如昂尼斯在1911年发现的那样，电流可以在没有电源的情况下无休止地流过超导线圈。它不是人们可能认为的完美导电性，而且无法用经典物理学解释。超导电性的第一个微观量子力学理论是由约翰·巴丁（John Bardeen）、利昂·库珀（Leon Cooper）和罗伯特·施里弗（Robert Schrieffer）在1957年提出的。在这一被称为BCS（Bardeen-Cooper-Schrieffer）的理论中，超导性是通过一对相反动量的电子通过交换声子相互作用，形成整数自旋的复合玻色子的凝聚而发生的。这个过程类似于氦-3中的超流动性。1972年，巴丁、库珀和施里弗因这项工作被授予诺贝尔物理学奖。[26]
玻色子、费米子和超对称
粒子存在玻色子和费米子这两类基本类型，而不是一类，这一事实促使物理学家寻找粒子的统一理论，提出两者之间的关系——这就是所谓的超对称（supersymmetry）。如果这种对称存在，它将把冷漠的费米子和抱团的玻色子聚集在一个单一大家庭中，并意味着存在许多未被发现的粒子。后者可以为标准模型中的许多疑难领域提供优雅的解决方案。在超对称中，每个玻色子和费米子都有一个与其相对类型的关联的粒子，称为超对称伙伴（superpartner）。例如，电子是费米子，它会有一个叫超电子（selectron）的超对称伙伴，它是玻色子。在完全超对称理论中，除了自旋不同，每一对超对称伙伴都有相同的质量和内部量子数。
但如果存在这样的“超级伴星”，它们应该早就被发现了。因此，人们推测，也许超对称是软破缺的（softly broken），从而允许超对称伙伴在质量上有所不同。如果这种理论是正确的，它将会解决一些重要的问题，诸如为希格斯玻色子的质量设定一个上限，并缓解因理论中不同尺度的巨大差异而产生的等级问题。物理学家抱有希望，他们之所以在标准模型中仍然面临这些问题，也许是因为迄今为止，他们只看到了图景的一半。
到目前为止，还没有实验证据表明超对称存在，也没有证据表明当前模型的其他扩展也许更为适用。研究超出标准模型物理（beyond the Standard Model），需要专门设计粒子加速器。升级后的大型强子对撞机的最新发展趋势让某些超对称研究阵营感到相当沮丧。[27]
玻色在欧洲
援用爱因斯坦1924年7月2日寄来的致谢明信片，玻色向达卡大学申请了两年的学习假期，去考察欧洲的实验室。他的请求立即得到了批准。他的第一站是巴黎，于10月18日抵达那里。他暂住在拉丁区的索梅拉街（rue du Sommerard）17号，那里是印度学者的天堂。他的主要兴趣是访问欧洲顶尖的实验室，亲身学习最新技术，特别是放射化学和X射线晶体学，这些实验工作与他在量子理论方面的理论研究相去甚远。他在到巴黎之前就已出名，所以访问从来都不是问题。但他与居里夫人第一次见面时发生的事情多少有些出人意料。带着熟悉他的工作的朗之万（Paul Langevin）的推荐信，他去见了居里，打算学习放射性方面的工作。用他自己的话来说，
我被允许进入她的小房间。那位伟大的老妇人坐在那里，一袭黑衣。我能从她的照片上认出她来。我把推荐信递给她。她亲切地跟我打招呼，说她不可能无视这样一个人的推荐信。她说，你肯定会有机会和我一起工作，但不是现在，而是三四个月后。要学会法语，否则你会发现在实验室工作很困难。我想你不着急吧。
她用纯正的英语从容地讲了大约十分钟。我没有机会告诉她我已经懂一点法语了。在过去的十年里，我一直在家里学法语。我告辞时表示会遵照她的指示去做。[28]
接下来的六个月里，玻色在路易斯·德·布罗意的哥哥莫里斯·德·布罗意（Maurice de Broglie）的实验室里学习X射线晶体学和光谱学。然后他回到居里的镭研究所，在那里工作了几个月。
他的下一个目的地是柏林，于1925年10月抵达。10月8日，他给爱因斯坦发了一封邮件，希望能约见他，但爱因斯坦当时不在柏林，所以直到他回来后他们才见面。此后，两人经常见面，就物理学和其他当时感兴趣的问题进行了广泛的讨论。他们对物质和辐射之间相互作用的概率有不同的看法，爱因斯坦认为自发辐射（spontaneous emission of radiation）是原子的内在属性，而玻色则认为这是新的统计的结果。
爱因斯坦给了玻色一封介绍信，这封信帮助他获得了从大学图书馆借书和参加物理报告会的必要特权。他也有机会见到重要的科学人物，如弗里茨·哈伯（Fritz Haber）、奥托·哈恩（Otto Hahn）、赫尔曼·马克（Herman Mark）、莉泽·迈特纳（Lise Meitner）、迈克尔·波兰尼（Michael Polanyi）、理查德·冯·米塞斯（Richard von Mises）和尤金·维格纳（Eugene Wigner）等。
玻色描述了当时在柏林令人激动的事。在给巴黎的一位物理学家扎多克-卡恩（Jacqueline Zadoc-Kahn）的信中，他写道:
柏林的每个人（每个物理学家）似乎都对物理学的进展感到非常兴奋，首先是去年（ [10月]28日），海森堡在研讨会上讲了他的理论，然后在最后一次研讨会上，有一个关于最近的自旋电子假设的长篇讲座（也许你听说过）。每个人都很困惑，很快就会有关于薛定谔论文的讨论。爱因斯坦似乎对此很兴奋。前几天，我们从讨论会回来，突然发现他跳了起来，就在我们坐的那个车厢里，爱因斯坦激动地谈起我们刚才听到的报告。他不得不承认，考虑到这些新理论所关联和解释的许多事情，这似乎是一件了不起的事情，但他对这一切的不合理性感到非常困扰。我们都沉默了，但他几乎一直在说，没有意识到他在其他乘客心中引起的兴趣和疑惑。[29]
回到达卡
回到达卡大学后不久，玻色被任命为教授、物理系主任和理学院院长。他开始利用他在欧洲获得的实验科学知识来改善国家的高等教育和科学研究，重新设计实验室，并开始在X射线晶体学、光谱学和晶体磁学方面进行研究。他还在化学领域做了大量工作，并指导他的朋友高什（Jnan Chandra Ghosh）的博士生。高什研究强电解质，经常不在学校。他并没有投身于理论化学，而是更喜欢亲自动手，合成和分析在当时具有实际意义的化学物质。这种理念可能来自他父亲的小型化工厂和他的老师，印度化学工业的奠基人普拉富拉·雷。玻色建立了一个小型化学实验室，鼓励学生合成吐根碱（emetine，艾美汀）、磺胺类药物（sulfa drugs）和其他药品。他的这些成果大部分从未发表，少数发表的论文也几乎没有他的名字。[30]
玻色博学多才，他在达卡大学的办公室变成了一个自由交流讨论的中心，话题从物理、化学、数学、统计学到文学、历史、语言学等等。在业余时间，他会解决困难的数学问题。克里什南（Kariamanikkam Srinivasa Krishnan）曾与拉曼一起发现了拉曼效应（Raman effect），后来加入了达卡大学，他说：“玻色博士能从复杂的问题中找到乐趣。一旦他解决了问题，他的热情就会消失。他把校样扔进废纸篓，根本懒得把它们寄给任何杂志。”[31]传说，博士生们会趁玻色不在的时候来收集这些被丢弃的证明，用在自己的博士论文中。
返回加尔各答
20世纪40年代印度独立运动风潮正盛。孟加拉的分治迫在眉睫，它被划分为西孟加拉邦和东孟加拉邦，达卡为首都。1945年，玻色带着沉重的心情离开达卡，成为加尔各答大学科学学院的凯拉（Khaira）物理学教授。他在那里一直工作到1956年退休。
在加尔各答，玻色也把他的工作时间花在实验科学，而不是理论物理上。他建立了一个X射线实验室，鼓励有机化学家通过X射线分析来确定分子结构。他还从事热致发光（thermoluminescence）研究，并开发了一种新的快速扫描技术来研究热致发光光谱的变化。这为快速连续扫描的研究开辟了新的途径。1954年，他在巴黎举行的第三届国际晶体学联合会大会（General Assembly of the International Union of Crystallography）上报告了这些研究结果。
玻色还设计了一种特殊的粉末相机和差热分析仪（differential thermal analyzer），用于分析从印度不同地区收集的粘土矿物的结构。他的学生A. K. 玻色和森古普塔（Purnima Sengupta）于1954年在《自然》杂志上发表了这些成果 [32]。这些努力可能不能打上他天才的印记，但是表明了他致力于为国家建立健全的科学文化。
他的同胞们一直在哀叹，像他这样天才的人本可以为科学做出更大的贡献；还有一些因为他未获得诺贝尔奖而残存的不满情绪——许多人仅仅因为证明了玻色是正确的而获得了诺贝尔奖。杰出的苏联物理学家、诺贝尔奖得主朗道（Lev Landau）提出了一个天才量表，对20世纪截至1968年最聪明的物理学家进行排名：按对数尺度划分，共五个等级。据他估计，一流（0.5级）物理学家的贡献是二流的10倍；他把爱因斯坦理所当然地放在了一流的首位，那些发展了量子力学的人在同一级，玻色也位列其中。朗道把自己安排在了下一级。[33]
在20世纪50年代初，玻色突然带着极大的热情回到了理论物理，特别是爱因斯坦的统一场论。他在不到两年的时间里写了五篇论文，其中四篇是用法语写的，解决了一些困难的数学问题[34]。这些是他最后的科学论文。虽然他们都发表在国际知名期刊上，但这些文章都没有出现在2014年的一篇统一场论综述中[35]。1955年，玻色期待在伯尔尼举行的庆祝相对论诞生50周年的国际会议上再次见到爱因斯坦，并与他讨论一些新的想法。会议原定于7月举行，但爱因斯坦于4月去世。爱因斯坦去世的消息传来时，他正在写一篇新的论文。据目击者说，他沉默了一会儿，然后把纸撕了，扔进了废纸篓。
1913年，泰戈尔成为第一位获得诺贝尔奖的非欧洲人。受到泰戈尔的启发，他花了相当多的时间用母语推广科学。1948年，他成立了一个名为Bangiya Bijnan Parishad（孟加拉科学委员会）的科学知识普及机构。
1956年从理学院退休后，玻色被任命为维斯瓦·巴拉蒂大学（Visva-Bharati University）的副校长，该大学是泰戈尔于1921年创建的。他在那里只工作了三年，之后在1959年被任命为国家物理学教授。1954年，他还被授予印度政府第二高平民奖——帕德玛·维布尚（Padma Vibhushan）奖，并宣誓就职为上院（Rajya Sabha）的国会提名议员。
1954年，狄拉克碰巧访问加尔各答，发现玻色尚未当选皇家学会（Royal Society）的会员，狄拉克回到英国，继续促成此事。直到1958年，国外的学术机构才正式承认了他对量子理论的贡献。
关于狄拉克访问加尔各答有一个有趣的故事。他和妻子一起来到这里，玻色和他的一些学生去火车站接他们。下了火车后，他们被带上玻色的小轿车，并被安排到后排座位上，而玻色和他的学生们则挤在前排座位。当费米—狄拉克统计的创建者之一的狄拉克礼貌地邀请一些学生坐到后排座位上时，玻色诙谐地说：“我们相信玻色统计。”
1974年2月4日玻色去世了。为了永久地纪念他，印度政府于1986年在加尔各答建立了玻色国家基础科学中心（S. N. Bose National Centre for Basic Sciences）。中心的资深物理学家马尔卡（Binay Malkar）曾经说：“只要宇宙中有光，玻色子就会无处不在。”[36]
参考文献
[1] Satyendra Nath Bose, “Plancks Gesetz und Lichtquantenhypothese,” Zeitschrift für Physik 26 (1924): 178–81, doi:10.1007/BF01327326. The article was translated into English in Satyendranath Bose, “Planck’s Law and the Light Quantum Hypothesis,” Journal of Astrophysics and Astronomy 15 (1924): 3–7, doi:10.1007/BF03010400.
[2] Bose is quoted to this effect in Giuseppe Bruzzaniti, Enrico Fermi: The Obedient Genius (New York: Springer, 2010), 82.
[3] Abraham Pais, Subtle Is the Lord: The Science and the Life of Albert Einstein (Oxford: Oxford University Press, 2005), 428.
[4] Max Planck, “Zur Theorie des Gesetzes der Energieverteilung im Normalspectrum,” Verhandlungen der Deutschen Physikalischen Gesellschaft 2 (1900): 146–151, doi:10.1002/phbl.19480040404; Niels Bohr, “On the Constitution of Atoms and Molecules, Part I,” Philosophical Magazine 26, no. 151 (1913): 1–24, doi:10.1080/14786441308634955; Niels Bohr, “On the Constitution of Atoms and Molecules, Part II,” Philosophical Magazine 26, no. 153 (1913): 476–502, doi:10.1080/14786441308634993; Niels Bohr, “On the Constitution of Atoms and Molecules, Part III,” Philosophical Magazine 26, no. 155 (1913): 857–75, doi:10.1080/14786441308635031.
[5] Meghnad Saha and Satyendra Nath Basu, “On the Influence of the Finite Volume of Molecules on the Equation of State (with S. N. Bose),” Philosophical Magazine Sr. VI, 36, no. 212 (1918): 199–202, doi:10.1080/14786440808635814.
[6] Wolfgang Pauli, “Über das thermische Gleichgewicht zwischen Strahlung und freien Elektronen,” Zeitschrift für Physik 18 (1923): 272–86, doi:10.1007/BF01327708.
[7] Bose, “Plancks Gesetz und Lichtquantenhypothese”; “Planck’s Law and Light Quantum Hypothesis,” Observations on Quantum Computing & Physics, June 10, 2012.
[8] Albert Einstein, “Quantentheorie des einatomigen idealen Gases [Quantum Theory of the Monatomic Ideal Gas],” Königliche Preußische Akademie der Wissenschaften: Sitzungsberichte (1924): 261–67; Albert Einstein, “Quantentheorie des einatomigen idealen Gases. Zweite Ab-handlung, Sitzungsberichte der Preußischen Akademie der Wissenschaften (Berlin),” Physikalisch-mathematische Klasse (1925): 3–14; Albert Einstein, “Zur Quantentheorie des idealen Gases [On the Quantum Theory of the Ideal Gas], Sitzungsberichte der Preußischen Akademie der Wissenschaften (Berlin),” Physikalisch-mathematische Klasse (1925): 18–25.
[9] Planck quoted in Abraham Pais, Niels Bohr’s Times: In Physics, Philosophy, and Polity (Oxford: Clarendon Press, 1991), 86.
[10] Planck quoted in Pais, Subtle Is the Lord, 384.
[11] Albert Einstein, Doc. 14, “On a Heuristic Point of View Concerning the Production and Transmission of Light (Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gisichtspunkt), Annalen der Physik 17 (1905),” in The Collected Papers of Albert Einstein: Vol. 2 The Swiss Years: Writings, 1900–1909, trans. Anna Beck (Princeton: Princeton University Press, 1989), 97.
[12] Władysław Natanson, “Über die statistische Theorie der Strahlung [About the Statistical Theory of Radiation],” Physikalische Zeitschrift 12 (1911): 659–66; Paul Ehrenfest and Heike Kamerlingh Onnes, “Simplified Deduction of the Formula from the Theory of Combinations which Planck Uses as the Basis of his Radiation Theory,” Proceedings of the Royal Netherlands Academy of Arts and Sciences 17 (1914): 870–73.
[13] Robert Millikan, “A Direct Photoelectric Determination of Planck’s ‘h’,” Physical Review 7, no. 3 (1916): 383, doi:10.1103/physrev.7.355.
[14] Quoted in Kameshwar Wali, ed., Satyendra Nath Bose—His Life and Times: Selected Works (With Commentary) (Singapore: World Scientific Publishing, 2009), 303.
[15] Bohr, “On the Constitution of Atoms and Molecules, Part I.”
[16] Max Planck, “Zür Theorie des Gesetzes der Energieverteilung im Normalspectrum [On the Theory of the Energy Distribution Law of the Normal Spectrum],” Verhandlungen der Deutschen Physikalischen Gesellschaft 2 (1900): 237–45; Max Planck, “Zur Theorie der Wärmestrahlung [On the Theory of Thermal Radiation],” Annalen der Physik 4, no. 31 (1910): 758–68, doi:10.1002/andp.19103360406; Peter Debye, “Der Wahrscheinlichkeitsbegriff in der Theorie der Strahlung [The Concept of Probability in the Theory of Radiation],” Annalen der Physik 338, no. 16 (1910): 1,427–34, doi:10.1002/andp.19103381617; Peter Debye, “Zerstreuung von Röntgenstrahlen und Quantentheorie [Scattering of X-rays and Quantum Theory],” Physikalische Zeitschrift 24 (1923): 161–66; Albert Einstein, “Zur Quantentheorie der Strahlung [On the Quantum Theory of Radiation],” Physikalische Zeitschrift 18 (1917): 121–28; Wolfgang Pauli, “Über das thermische Gleichgewicht zwischen Strahlung und freien Elektronen [About the Thermal Equilibrium between Radiation and Free Electrons],” Zeitschrift für Physik 18 (1923): 272–86, doi:10.1007/bf01327708; Albert Einstein and Paul Ehrenfest, “Zur Quantentheorie des Strahlungsgleichgewichts [On the Quantum Theory of Radiation Equilibrium],” Zeitschrift für Physik 19 (1923): 301–306, doi:10.1007/bf01327565.
[17] A facsimile of the letter is available in Somaditya Banerjee, “Bhadralok Physics and the Making of Modern Science in Colonial India” (PhD thesis, University of British Columbia, 2018), Appendix C.
[18] Banerjee, “Bhadralok Physics,” 93.
[19] A facsimile of the German original is available in Banerjee, “Bhadralok Physics,” Appendix D.
[20] Chandrasekhara Venkata Raman and Suri Bhagavantam, “Experimental Proof of the Spin of the Photon,” Indian Journal of Physics 6 (1931): 353.
[21] Paul Dirac, The Principles of Quantum Mechanics, 3rd edn. (Oxford: Clarendon Press, 1947).
[22] See Pais, Subtle Is the Lord, 436–37.
[23] He presented his results at the Königliche Preußische Akademie der Wissenschaften meetings on July 10, 1924; January 8, 1925; and January 29, 1925.
[24] “Press Release: The Nobel Prize in Physics 2001,” NobelPrize.org.
[25] David Aveline et al., “Observation of 玻色–Einstein Condensates in an Earth-Orbiting Research Lab,” Nature 582, no. 7,811 (2020): 193–97, doi:10.1038/s41586-020-2346-1.
[26] Bardeen, Cooper, and Schrieffer were awarded the Nobel Prize in Physics for this work in 1972.
[27] Paul Sutter, “From Squarks to Gluinos: It’s Not Looking Good for Supersymmetry,” Space.com, January 7, 2021; and Scott Hershberger, “The Status of Supersymmetry,” Supersymmetry: Dimensions of Particle Physics, January 12, 2021.
[28] Wali, Satyendra Nath Bose, 279–80.
[29] Wali, Satyendra Nath Bose, 453.
[30] This fact can be gleaned from memoirs by chemists who worked under Bose’s guidance such as Pratul Chandra Rakshit, Periye Elam (1995), and Asima Chatterjee, “Contributions of Professor S N Bose, FRS in Chemistry,” Science and Culture 40, no. 7 (1974): 295–97. See also A. K. Bose and Purnima Sengupta, “X-Ray and Differential Thermal Studies of Some Indian Montmorillonites,” Nature 174 (1954): 40–41, doi:10.1038/174040a0.
[31] Chanchal Kumar Majumdar et al., eds., S. N. Bose: The Man and His Work, Part II: Life, Lectures and Addresses, Miscellaneous Pieces (Calcutta: S. N. Bose National Centre for Basic Sciences, 1994), 63.
[32] Bose and Sengupta, “X-Ray and Differential Thermal Studies of Some Indian Montmorillonites.”
[33] See Paul Ratner, “Landau Genius Scale Ranking of the Smartest Physicists Ever,” Big Think: Hard Science, September 28, 2020. ↩
[34] See Santimay Chatterjee and Chanchal Kumar Majumdar, eds., S. N. Bose: The Man and His Work, Part I: Collected Scientific Papers (Calcutta: S. N. Bose National Centre for Basic Sciences, 1994), 274–95. ↩
[35] Hubert Goenner, “On the History of Unified Field Theories,” Living Reviews in Relativity 7, no. 2 (2004): 1–153, doi:10.12942/lrr-2004-2. ↩
[36] Binay Malkar, “The Forgotten Quantum Indian,” The Statesman, December 19, 2018. For further reading, see Chatterjee and Majumdar, eds., S. N. Bose: The Man and His Work, Parts I and II; the Prof. S. N. Bose Archive at the S. N. Bose National Centre for Basic Sciences; Jagdish Mehra, “Satyendra Nath Bose,” Biographical Memoirs of Fellows of the Royal Society 21 (1975): 116–54, doi:10.1098/rsbm.1975.0002; Wali, Satyendra Nath Bose.
作者简介：Patha Ghose是加尔各答泰戈尔自然科学与哲学中心的杰出研究员，也是印度国家科学院和西孟加拉邦科学技术学院的研究员。他于1999年退休，担任加尔各答玻色国家国家基础科学中心的教授和学术项目协调员。他在玻色的指导下完成了博士论文，专门研究量子力学和经典偏振光学的基础。
本文经作者授权翻译发表于《返朴》，译自Partha Ghose, Satyendra Nath Bose: Counting in the Dark, 原文链接：
https://inference-review.com/article/counting-in-the-dark#footnote-17。
出品：科普中国
0
推荐
京公网安备 11010502034662号 