根据一张湖上落日的照片，普林斯频大学范德北教授（Robert J. Vanderbei）证明了地球是圆的，并且给出了地球的半径。

撰文 | 姬扬（中国科学院半导体研究所）、高国强（哈尔滨工业大学（威海））

知道某件东西可以做出来，就是最大的提示。只要知道某件东西可以做出来，即使不知道它到底是怎么做的，很多人就可以把它做出来。在科学发展的历史上，这样的事情屡见不鲜。

比如，伽利略发明望远镜。其实，伽利略并不是发明望远镜的第一人。1609年5月， 伽利略偶然听说，荷兰有人发明了一种“幻镜”，能够看到远处的风景。他没有参观或购买这种“幻镜”，而是自己动手，用了不到 3 个月的时间，仿造了两架仪器，并用它仰视星空。他观测到了月球的高地和环形山投下的阴影，发现了太阳黑子，还发现了木星的4个最大的卫星。借助于望远镜，伽利略还先后发现了土星光环、太阳的自转、金星和水星的盈亏现象、月球的周日和周月天平动，以及银河是由无数恒星组成，等等。

下面这个例子发生在现代。

2008年7月5日，在密执安湖湖边，普林斯顿大学的范德北教授（Robert J. Vanderbei）拍摄了一张夕阳照片，太阳即将落入地平线以下，在湖面上留下了倒影。范德北教授认识到，利用这张照片，再加上一些中学的物理和数学知识，就可以证明地球是圆的，还可以得到地球的半径。

图1 美国密执安湖上的夕阳。普林斯顿大学的范德北教授在2008年7月5日拍摄。

01基本知识

这里需要的物理知识是：光沿直线传播；光被镜子反射的时候，入射角等于反射角。

这里需要的数学知识是：勾股定理，两个直角边的平方和等于斜边的平方；三角形的正弦定理，即三角形的边长与对角的正弦成正比。

要点在这里：水面就像镜子一样是平的，可以反射太阳光。但是，镜子或者水面的“平”是局部的平，而地球表面是弯曲的，你和我站在两个不同的地方，你的“平”在我这里就是“斜”了。对于平行入射的太阳光来说，不同地方的水面相对于太阳光的倾角是不同的。

这个分析很直接，但是有些繁琐。下面我们把分析过程详细地写出来，让《中学生数理化（初中版）》的读者也能懂。我们建议读者先试着自己推导，如果遇到困难，再回来看我们的解释。我们当初也是只知道结论，就自己推导出来了。这个问题的难度不在于推导，而在于认识到，这张图片包含了结论所需的全部信息。

02模型和推导

我们分析的示意图（图2）跟范德北教授的类似，只是为了详细说明，用一些新的符号做了标注，分析的过程也略有不同。具体说明如下:

• 对应于地球的球心，弧线对应于地球表面（假设是完美的球面），是地球的半径；
• 是照相机的位置，照相机相对于水面的高度，也就是的长度；
• 是照相机看到的地平线的位置；是和两个点相对于地球中心的张角；
• 是太阳的上沿在水面的倒影位置；是该处太阳光与水面的夹角；
• 是残阳相对于照相机的张角，也就是太阳最上沿和地平线相对于照相机的夹角；
• 是残阳在水面上的倒影相对于照相机的张角，太阳最上沿的水面倒影和地平线相对于照相机的夹角；
• 是Q和R两点相对于照相机的夹角。

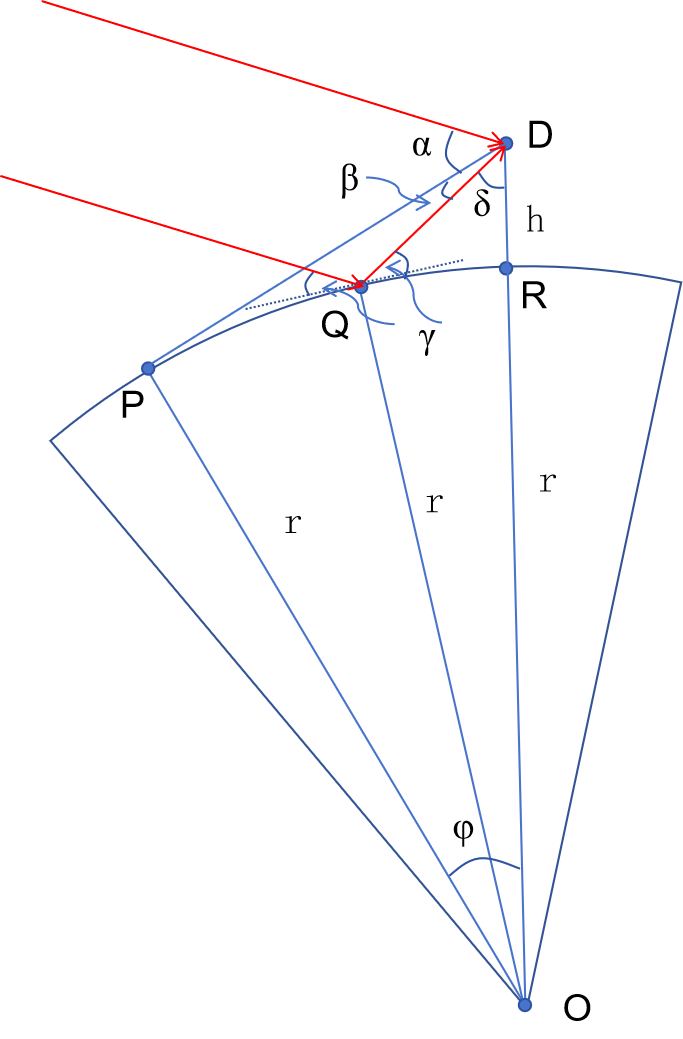
图2 湖上落日照片的分析示意图。

因为太阳离地球很远，可以认为来自太阳上沿的光是平行的，也就是图2中从左上方入射的两条红色光线，一条光线直接照射到照相机，另一条在水面点处反射后进入照相机（点处的虚线表示该处的水平线）。根据反射定律和平行线内角和定律，可以知道因为是直角三角形（点是看到的地平线，意味着垂直于半径），所以其中，弧度制的 等于 90° 。另外，所以，对三角形应用正弦定理，我们有也就是说在直角三角形中，我们有根据上述两个公式与三角形诱导公式，就可以得到所以最后得到这里用到了三角函数的和差化积公式。因为所以，我们有请注意，()和()都是精确的公式，没有任何近似。在 的情况下，我们有近似公式

03数据分析

范德北教授对照片进行了数据分析（图3）：太阳的直径是317个像素，地平线上的太阳高度是个像素，地平线以下的（也就是水面上的）太阳影像的高度是个像素。因为阳的视张角是，这样就可以得到和的值, 也就得到了的值。而就是照相机三脚架的高度，大约是米。把这些数据带入公式()，就有米（这个值不确定）图3  范德北教授对湖面夕阳的数据分析。可以得到地球的半径为公里与实际值公里相差不远。如果用地球半径倒推的值，可以得到大约是 米，似乎比米更符合三脚架上的相机高度了。但是，这有些过于精确了，这个简单的模型没必要这么精确吧？

04讨论

简而言之，地球很大，要想知道它是不是圆的，甚至测量它的半径，需要跑得很远才行。

但是，普林斯顿大学的范德北教授认识到，只需要在海边（或者很大的湖也可以）拍一张日出或日落的照片，就可以证明地球是圆的，还可以得到地球的半径。而且这里的道理很简单，中学生也可以理解一一困难在于，你首先要认识到，根据这张照片就可以得到所有这些信息。

事后看来，这个分析很简单，但是第一个认识到真相的人，还是很了不起的，关键他认真想了。可能以前也有人想过了，甚至写出来了。重要的事情总是会被发现很多次的。

一方面，太阳底下没有新鲜事；另一方面，新概念、新方法和新的测量仪器带来了新的认识，深入思考天天看到“理所当然”的现象，有时候也会有收获。人们很早就应该能认识到地球是圆的，但总是差了一点儿。

比如说，在春秋战国时代，我们就知道: “孔子登东山而小鲁，登泰山而小天下” (《孟子・尽心上》) ; “吾尝跂而望矣，不如登高之博见也” (《荀子・劝学》)。现在看起来，这后面的是显然的：登高则视野广阔，因为地平线后退了。

当然，这只是定性的认识，而孟子和荀子也没有推断出地球是圆的。定量的也有。在《论衡・说日》篇里，东汉时期的王充说：“试使一人把大炬火夜行于道，平易无险，去人十里，火光灭矣。”在平原上，一个人拿着火把在夜里行走，他走出大概十里之外，你就看不到火把了。这里有了“十里”这个定量的数据，而火把离地面的高度大概也就一两米，由此推算出地球的直径大约是几万里。

可惜的是，王充却认识不到这一点，而是把这个作为“盖天说”的证据，反驳（我们现在看起来更有道理的）“浑天说”。

当然，很早就有人猜地球是圆的，比如中国古代的慎子和张衡，古希腊的毕达哥拉斯和亚里士多德。

据说，在公元前 3 世纪，古希腊天文学家埃拉托色尼根据正午射向地球的太阳光和两观测地的距离，首次算出地球的周长。公元726年，唐代天文学家一行禅师主持了全国天文大地测量，利用北极高度和夏天的日长，计算出了子午线一度之长和地球的周长。这篇文章也许还可以回答一个常见的问题：教科书为什么不能写得详细一些? 答案是, 可以写得更详细，但是书就变得太厚了。

关于湖边落日的分析，还有很多因素和细节没有考虑。请思考一下，它们会怎样影响分析的结果呢?比如说，如果在同一天，在世界各地拍这样的照片，得到的结果会不一样；即使在同一个地方，在不同的日子拍这样的照片，结果也会不一样。因为地球绕着太阳转（在黄道面上），而且地球的自转轴并不垂直于黄道面。所以，如果在同一个地方拍很多天的照片，或者在同一天在很多地方拍照片，都能得到很多信息，包括而不限于：地球是圆的，地球的半径，自转轴相对于黄道面的央角，照片拍掫地的纬度，等等。

当然，你可能还会认识到，这跟日晷也有相似之处啊。坚个杆子看日影，同一个地方观察一年，或者同一天记录很多地方，也能得到这样的信息。古代人没有照相机，但是他们也会观察，也会思考。

05打油诗一首

这回书，有分教：

傍晚湖边散步，忽然灵光闪现，天上有个太阳，水面反射影像。由此可以知道，大地是个圆球，

利用几何知识，得到地球半径。

参考文献

[1] Robert J. Vanderbei, The earth is not flat: An analysis of a sunset photo, Optics & Photonics News (OPN), 34-39, November 2008.[2] https://vanderbei.princeton.edu/FRS_131/lectures/lec3.pdf

本文受科普中国·星空计划项目扶持

出品：中国科协科普部

监制：中国科学技术出版社有限公司、北京中科星河文化传媒有限公司