编译 | 王庆法

两位研究人员证明了彭罗斯密铺（Penrose Tilings），这种永不重复的著名图案，在数学上相当于一种量子纠错方法。

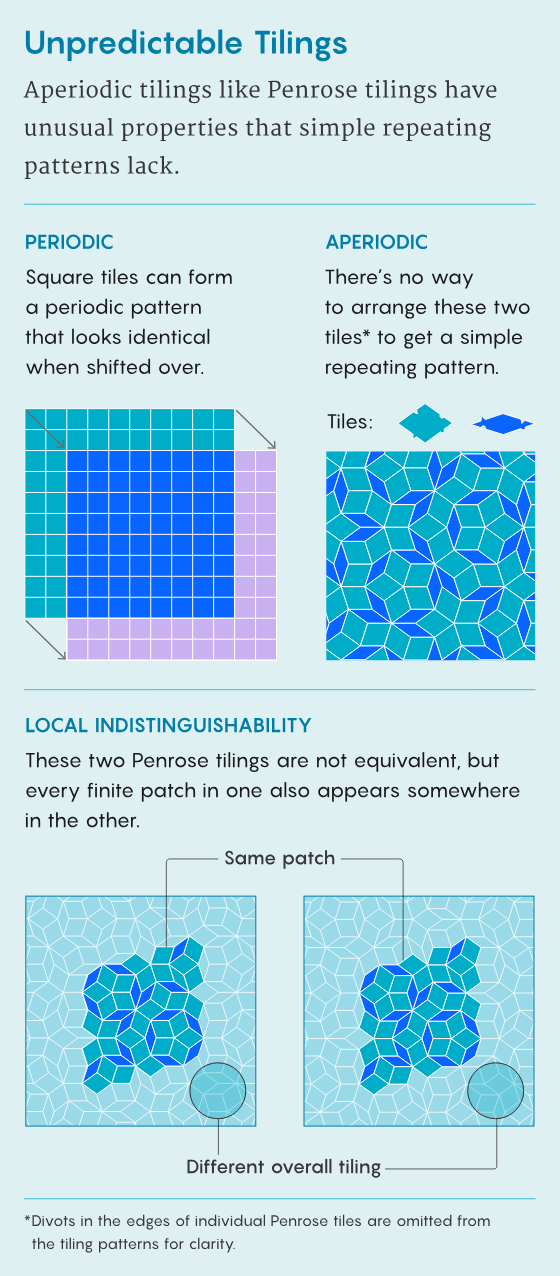
如果你想给浴室地板铺瓷砖，正方形瓷砖是最简单的选择——它们能够以网格模式无缝拼接，并且可以无限延伸。这种正方形网格具有许多密铺共同的特性：将整个网格按固定量移动，结果产生的图案与原始图案无法区分。但是对许多数学家来说，这样的“周期性”密铺是无聊的。如果你见过一个小块区域，就等于已经见过全部。

在20世纪60年代，数学家们开始研究具有更丰富行为的“非周期性”密铺集。也许最著名的是在20世纪70年代由多才多艺的物理学家、未来诺贝尔奖得主罗杰·彭罗斯发现的一对菱形密铺。这两块密铺的副本可以形成无限多不同的图案，可以永远持续下去，称为彭罗斯密铺。然而，无论你如何排列密铺，你都不会得到周期性重复的图案。

“这些是本不应该存在的图形，”布里斯托大学的物理学家尼古拉斯·布鲁克曼说道。

半个多世纪以来，非周期性密铺一直吸引着数学家、业余爱好者以及许多其他领域的研究人员。现在，两个物理学家发现了非周期性密铺与计算机科学中看似不相关的一个分支之间的联系：研究未来量子计算机如何编码信息以保护其免于错误。2023年11月发布在预印本服务器arxiv.org上的一篇论文^[1]中，研究人员展示了如何将彭罗斯密铺转化为一种全新的量子纠错码。他们还基于其他两种非周期性密铺构建了类似的纠错码。

这两者之间的对应关系的核心是一个简单的观察：在非周期性密铺和量子纠错码中，了解大型系统的一小部分对整个系统的了解毫无帮助。（译者注：类比思维的力量 ）  

“这似乎是事后看起来显而易见的美妙之处，”伦敦大学学院的量子信息研究员托比·库比特说道。“你会想，‘为什么我没想到呢？’”     

普通计算机使用具有两种不同状态的比特表示信息，标记为0和1。量子比特或量子位也有两种状态，但它们还可以被引导进入所谓的叠加态，其中0和1状态共存。通过利用涉及多个量子位的更复杂的叠加态，量子计算机可以比任何传统机器更快地执行某些计算。

然而，量子叠加态是敏感的怪物。测量叠加态中的量子位，它将塌缩到0或1，抹除任何正在进行的计算。更糟糕的是，由于量子位与其环境之间微弱的相互作用而产生的错误，可能产生对测量的破坏性影响。任何以错误方式与触碰量子位的事物，无论是好奇的研究人员还是离群的光子，都可能破坏计算。

彭罗斯脚下的瓷砖

这种极度脆弱性可能使量子计算听起来没有希望。但在1995年，应用数学家彼得·肖尔发现了一种巧妙的方法来存储量子信息。他的编码具有两个关键属性。首先，它可以容忍只影响单个量子位的错误。其次，它附带了一种纠正错误的程式，防止它们堆积并使计算脱轨。肖尔的发现是第一个量子纠错码的例子，它的两个关键属性是所有此类代码的决定性特征。

第一个特性源自一个简单的原则：秘密信息在被分割后会更不易受影响。间谍网络采用了类似的策略。每个间谍对整个网络的了解都很少，因此即使任何个体被捕，组织仍然安全。量子纠错码将这种逻辑发挥到极致。在一个量子间谍网络中，没有单个间谍会知道任何东西，但它们在一起会知道很多。

每个量子纠错码都是一种特定的方案，将量子信息分布在许多量子位中，形成一个集体叠加态。这种程序有效地将一组物理量子位转化为单个虚拟量子位。多次重复这个过程，使用大量量子位，你会得到许多虚拟量子位，可以用于执行计算。

组成每个虚拟量子位的物理量子位就像那些不知情的量子间谍。测量其中任何一个，你都不会了解它所属的虚拟量子位的状态——这是一种被称为局部不可区分性（local indistinguishability）的属性。由于每个物理量子位都不编码任何信息，单个量子位的错误不会破坏计算。重要的信息以某种方式无处不在，但又不在任何特定地方。

“你不能将它归结到任何一个单独的量子位，”库比特说道。

所有量子纠错码都可以吸收至少一个错误，而不会对编码的信息产生任何影响，但它们最终会随着错误的积累而沦陷。这就是量子纠错码的第二个特性——实际的错误纠正发挥作用的地方。这与局部不可区分性密切相关：由于单个量子位中的错误不会破坏任何信息，总是可以使用每个纠错码特定的既定程式来逆转任何错误。

加拿大滑铁卢大学的理论物理学Perimeter研究所的博士后李智对量子纠错理论十分精通。但当他与同事博伊尔（Latham Boyle）交谈时，这个主题离他的思考还很远。那是2022年秋天，两位物理学家在从滑铁卢到多伦多的夜间穿梭巴士上交谈。博伊尔是一位擅长非周期性密铺的专家，当时住在多伦多，现在在爱丁堡大学。在这些穿梭巴士行程中，他是一个熟悉的面孔，这些巴士常常会陷入交通堵塞。

“通常情况下，拥堵可能非常难熬，”博伊尔说道，“这一次是所有时间中最棒的一次。”  

在那个决定性的夜晚之前，李智和博伊尔彼此了解对方的工作，但他们的研究领域并不直接重叠，他们从未进行过一对一的对话。但与无数其他领域的研究人员一样，李智对非周期性密铺感到好奇。“很难不对它感兴趣，”他说。

当博伊尔提到非周期性密铺的一个特殊属性——局部不可区分性时，兴趣变成了迷恋。在这个背景下，这个术语意味着不同的东西。同一套密铺可以形成无数个看起来完全不同的密铺，但通过检查任何局部区域，不可能区分任何两个密铺。这是因为任何密铺的有限的小块区域，无论多大，都会在其他密铺中某处出现。

“如果我让你在一个密铺中或另一个密铺中停下来，并让你用一生的时间去探索，你永远也不会知道我让你停在哪个密铺，”博伊尔说道。

对李智来说，这看起来和量子纠错中的局部不可区分性的定义非常相似。他提到了这个连接，博伊尔立刻被吸引了。两者之间的数学基础是非常不同的，但这种相似之处令人着迷，不容忽视。

李智和博伊尔想知道他们是否可以通过基于一类非周期性密铺构建量子纠错码，来在这两个局部不可区分性的定义之间建立更精确的联系。他们在整个两个小时的穿梭巴士旅程中继续讨论，到了多伦多，他们确定这样的代码是可能的——只需构建一个正式的证明。（译者注：这就是大模型学习了各种范畴关系之后的可怕之处，毕竟范畴就是关系，关系的关系，关系的关系的关系。）

李智和博伊尔决定从彭罗斯密铺开始，这种密铺简单且熟悉。要将它们转化为量子纠错码，他们首先需要定义在这个不寻常的系统中量子态和错误会是什么样子。这部分很容易。用彭罗斯密铺覆盖的无限二维平面，如同量子位网格，可以使用量子物理学的数学框架进行描述：量子态是特定的密铺而不是0和1。一个错误简单地删除了密铺模式的一块区域，就像量子位阵列中的某些错误会抹去小集群中每个量子位的状态。

下一步是识别不会受到局部错误影响的密铺配置，就像普通量子纠错码中的虚拟量子位状态一样。解决方法与普通纠错码中的方法一样，是使用叠加态。精心选择的彭罗斯密铺叠加态类似于世界上最优柔寡断的室内设计师提出的浴室瓷砖排列。即使那种混乱蓝图的一部分缺失了，也不会泄露任何关于整个平面布局的信息。

为了让这种方法奏效，李智和博伊尔首先必须区分不同彭罗斯密铺之间的两种定性不同的关系。给定任何一个密铺，你可以通过在任意方向上平移或旋转它来生成无限数量的新密铺。通过这种方式生成的所有密铺的集合被称为等价类。

但并不是所有的彭罗斯密铺都属于同一等价类。一个等价类中的密铺无法通过任何组合的旋转和平移转化为另一个类中的密铺——这两个无限的模式在定性上是不同的，但仍然在局部上不可区分。 

通过建立这一区别，李智和博伊尔终于可以构建一个纠错码了。回顾一下，在普通量子纠错码中，一个虚拟量子位是以物理量子位的叠加态编码的。在他们基于密铺的纠错码中，类似的状态是单个等价类内所有密铺的叠加态。如果平面以这种叠加态铺设，可以在不暴露整体量子态信息的情况下填补空隙。

“彭罗斯密铺在量子计算机发明之前就不知何故了解了量子纠错，”博伊尔说道。

李智和博伊尔在巴士旅程中的直觉是正确的。在深层次上，这两个局部不可区分性的定义本身是不可区分的。

尽管在数学上定义明确，李智和博伊尔的新纠错码几乎不可行。彭罗斯密铺中的密铺边缘不是以规则的间隔出现的，因此指定它们的分布需要连续的实数而不是离散的整数。而另一方面，量子计算机通常使用离散系统，如量子位网格。更糟糕的是，彭罗斯密铺在无限平面上局部不可区分，这在有限的现实世界中并不适用。

博伊尔与李智一起基于非周期性密铺构建了量子纠错码   

“这是一种非常奇妙的联系，”代尔夫特理工大学的量子计算研究员芭芭拉·特哈尔说道。“但实际一点也是好的。”

李智和博伊尔已经在这方面迈出了一步，通过构建另外两种基于密铺的纠错码，其中一种量子系统在一个案例中是有限的，另一个案例中是离散的。离散纠错码也可以变得有限，但其他挑战依然存在。这两种有限纠错码只能纠正聚集在一起的错误，而最流行的量子纠错码可以处理随机分布的错误。尚不清楚这是基于密铺的代码的固有限制，还是可以通过更巧妙的设计来规避。

“还有许多后续工作可以进行，”布里斯托大学的物理学家费利克斯·弗利克说道。“所有好的论文都应该这样。”

需要更深入理解的不仅仅是技术细节——新的发现也引发了更多基本问题。一个明显的下一步是确定其他哪些密铺也可以用作纠错码。就在去年，数学家们发现了一族的非周期性密铺，每一个都只使用一种密铺。“看看这些最新的发展可能如何与量子纠错问题相联系，将会非常有趣，”彭罗斯在一封电子邮件中写道。

另一个方向是探索量子纠错码与某些量子引力模型之间的联系。在2020年的一篇论文中，博伊尔、弗利克和已故的马德琳·迪更斯展示了非周期性密铺在这些模型的时空几何中出现。但这种联系源自密铺的一个在李智和博伊尔的工作中不起作用的属性。似乎量子引力、量子纠错和非周期性密铺是一个谜题的不同部分，研究人员刚刚开始理解它们的轮廓。与非周期性密铺本身一样，弄清这些部分如何组合在一起可能非常微妙。

“这些不同事物之间有深厚的根基，”弗利克说道。“这一系列诱人的联系正等待被弄清楚。”