莫比乌斯带最有趣的特性之一是它的不可定向性,这意味着它没有明显的“上”或“下”面。它是拓扑学中一个引人入胜的研究课题,为复杂而迷人的数学形状和形式世界提供了巨大的见解。
编译 | B座17楼

莫比乌斯带是一种具有一条边界和一个表面的空间结构。
它可以通过取一条矩形纸条,将其扭转一半,然后将两端粘在一起来制成。
它有一个特性,如果你沿着带子的中间画一条线,你最终会回到你开始的地方,但在带子的另一边。

如果沿着中线切割莫比乌斯带,您将得到一个带有两次扭曲的单个环,而不是两个单独的环。
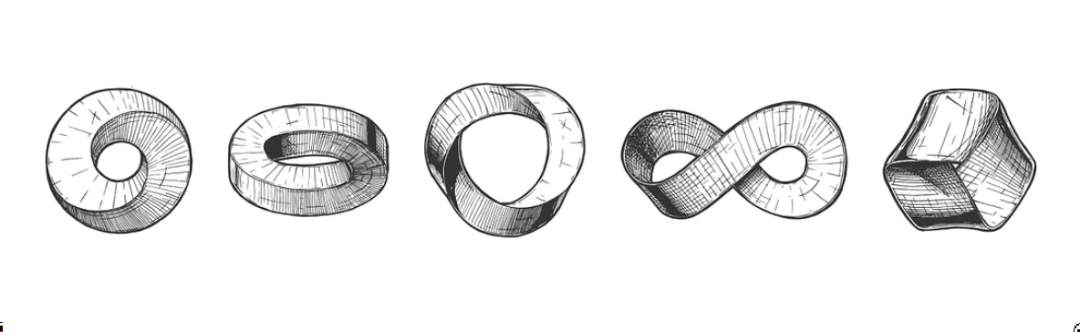
Infinity in a Twist: Understanding the Möbius Strip
莫比乌斯带最有趣的特性之一是它的不可定向性。这意味着它没有明显的“上”或“下”面。
如果你把一只蚂蚁放在条带上,它可以探索整个表面,而不会到达边缘或遇到边界。
除了理论上的魅力之外,莫比乌斯带还具有很多实际应用。例如,在材料科学中,莫比乌斯形分子,称为莫比乌斯芳烃,具有独特的电子特性,使其在有机半导体和导电聚合物的开发中发挥重要作用。
转折中的无限:了解莫比乌斯带
想想我们的日常生活中有多少与数学有关,这真是令人着迷,数学是一门只存在于我们脑海中的学科。
从平衡支票簿到计算前往月球等新目的地所需的时间,我们依靠数学原理做出明智的决定。
即使是最简单的任务,比如在烹饪美味的意大利面条阿尔弗雷多时测量成分,也涉及在某种程度上使用数学。
它证明了该主题的无处不在,以及人类思维创造并将其应用于我们日常生活各个方面的力量。

即使是无限的概念,一个几千年来一直吸引人类智力的概念,也可以被看作是从我们意识深处诞生的数学结构。
几千年来,各种哲学家和数学家一直在努力概括和定义无穷的真正含义,但这个难以捉摸的概念似乎总是从他们的智力掌握中溜走。
然而,这一切都在大约一个世纪前发生了变化,因为数学领域的杰出人物乔治·康托尔(Georg Cantor)的开创性工作改变了这一切。
康托尔经常被誉为现代数学之父,他毕生致力于对无穷的理解和阐释。他的开创性工作最终提出了一种在数理逻辑范围内理解无穷大概念的方法,为以前抽象的、无形的想法提供了一个有形的结构。
康托尔几乎一生都在思考和发现,这使他成为现代数学之父。
事实上,在康托尔之前,另一位数学家也设法用他设计的数学对象以具体的方式表达了无穷大。
德国数学家和天文学家奥古斯特·费迪南德·莫比乌斯(August Ferdinand Möbius)于1858年向世界介绍了这个有趣的物体。

奥古斯特·费迪南德·莫比乌斯的肖像丨来源:Wikimedia
虽然当时莫比乌斯没有以自己的名字命名这个物体,但它后来被称为“莫比乌斯带”。
这个独特的、片面的物体将成为无限的有力象征,为一个长期无法具体表现的概念提供有形的例证。
在其最基本的形式中,莫比乌斯带可以被描述为一个没有正面或背面的表面,而是一个连续的面。
这样的描述最初可能看起来令人困惑,甚至可能难以置信。
然而,一个简单的实验可以帮助阐明这个概念。拿一张纸条,在将两端连接在一起之前,先把一端扭转180度——瞧,你已经创造了一个莫比乌斯带。

如何制作莫比乌斯带的说明 |来源:Comsol
现在,在不抬起铅笔的情况下,拿笔沿着表面中间画一条线。在看似不同的两边画画,令人惊讶的是,你最终会回到你的起点。

然而,你从来没有真正翻转过条带或将铅笔移到另一边。这就是莫比乌斯带的魔力,一个以有形形式真正体现无限抽象概念的物体。
莫比乌斯带确实是无限的深刻类比。
想象一下,在这条带上放一些蚂蚁;蚂蚁可以无限期地行走,而不需要停下来或改变方向。

这种永恒的循环反映了无限的概念,其中结束和开始是无法区分的。
应用这个概念,我们可以欣赏到回收符号设计背后的原因,其灵感来自莫比乌斯带。三个追逐的箭头形成一个没有开始或结束的循环,代表了循环的连续循环。
它表明,产品一旦使用,不仅不会在自然界中消失,而是被回收并转世为新的形式,准备再次使用。
这种循环过程反映了莫比乌斯带的无限循环,使人们认识到可持续实践和资源保护的重要性。
在拓扑学领域——数学的一个分支,莫比乌斯带占有重要地位。拓扑学从根本上研究在拉伸和弯曲等连续变换下保留的空间特性,而不是撕裂或粘合。
根据这种推理,咖啡杯和甜甜圈被认为是相同的,或者说是“拓扑等价的”,因为一个可以通过拉伸和弯曲变成另一个。
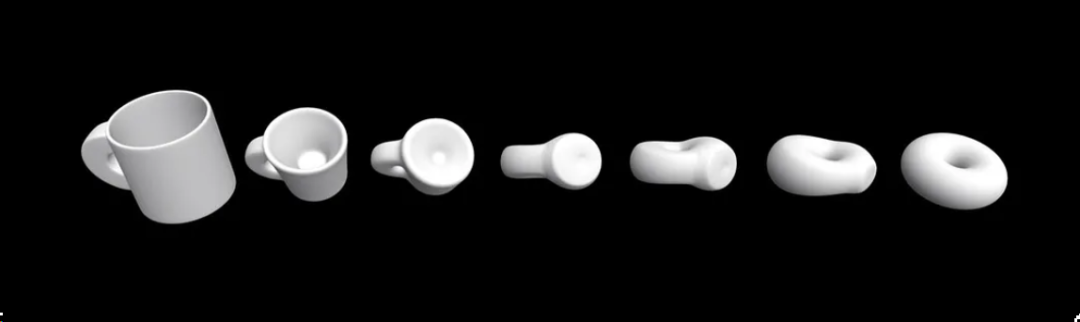
咖啡杯变形成甜甜圈丨来源:Sketchfab
拓扑学中的关键概念之一是“拓扑不变”的概念,即在这些连续变换下保持不变的属性或特征。这就是莫比乌斯带变得极其重要的地方。
它只有一侧的独特性质是拓扑不变量。无论您如何拉伸或弯曲莫比乌斯带,它始终具有一条连续的边。
这使得莫比乌斯带成为拓扑学中一个引人入胜的研究课题,为复杂而迷人的数学形状和形式世界提供了巨大的见解。
莫比乌斯带在现实生活中的应用
莫比乌斯带不仅是一个有趣的数学模型,也是一种实用的设计,可以提高日常物品的效率。
一个典型的例子可以在机场的喧嚣中找到,在那里,运送我们行李的传送带被设计成莫比乌斯条。
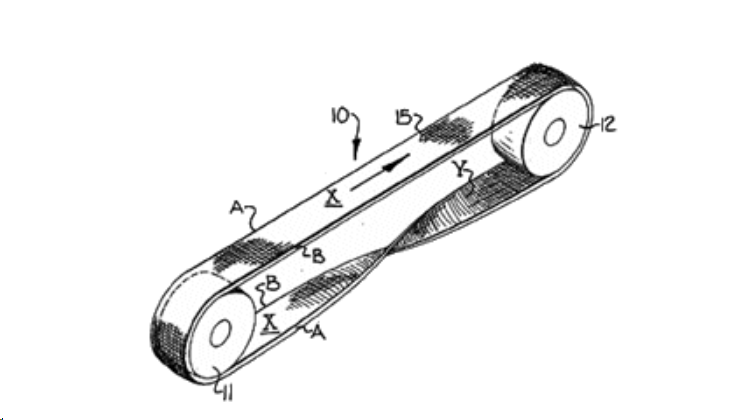
这种巧妙的设计确保了皮带表面的均匀磨损,从而延长了其使用寿命。同样,汽车中的风扇皮带也是按照相同的原理设计的。
通过采用莫比乌斯带的单面设计,风扇皮带的整个表面积都投入使用,导致均匀磨损。
这不仅延长了皮带的使用寿命,还提高了车辆的整体效率和性能。这种实际应用强调了莫比乌斯带对改善我们日常生活的重大影响,将无限的抽象概念转化为有形的现实。
莫比乌斯带式输送带的使用寿命更长!
在音频技术领域,莫比乌斯带已显著应用于盒式磁带录音,特别是无限循环盒式磁带。
这些磁带在答录机和车载播放器中特别受欢迎,其设计允许连续播放,而无需手动翻转。这是通过将莫比乌斯条概念应用于胶带设计来实现的。
在连接两端之前,磁带被扭曲了180度,从而形成了莫比乌斯带。这样一来,磁带就可以在两面读取,有效播放时间延长了一倍,
同时确保了无缝、不间断的音频体验。在这里,莫比乌斯带的无穷大原理再次被证明有助于增强技术设计。
艺术形式的莫比乌斯带
然而,莫比乌斯带不仅限于复杂数学和可持续实践领域;它也进入了艺术世界。
这个数学对象的有趣表现首次出现在荷兰图形艺术家莫里茨·科内利斯·埃舍尔(Maurits Cornelis Escher)的画作中,他以数学风格的作品而闻名。

埃舍尔的艺术经常玩弄无限和悖论的概念,而莫比乌斯带被证明是他探索的完美主题。
在他最著名的作品之一“莫比乌斯大道II(红蚂蚁)”中,描绘了一群蚂蚁穿越大道上永无止境的表面。
这种抽象数学概念的视觉表现不仅展示了数学与艺术之间的交叉,也挑战了我们的感知,揭示了艺术与科学交织在一起时出现的迷人和令人费解的可能性。
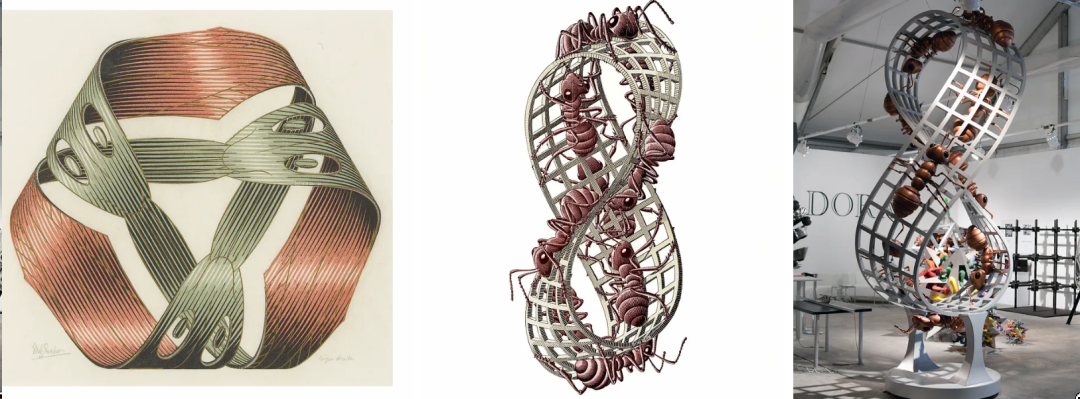
左:埃舍尔的莫比乌斯带 |M. C. Escher 的 Moebius Strip II |右:扎多拉的莫比乌斯大道二号
在2006年,一位名叫蒂姆·霍金森(Tim Hawkinson)的艺术家深受莫比乌斯带的启发,创作了一件名为“莫比乌斯船”的非凡木制雕塑。
这座非凡的雕塑呈无限循环,完美地反映了其同名的独特属性。霍金森用大多数人会忽略的普通物品——扎带和包装材料——建造了这个10米宽的杰作。
这些不起眼的元素汇集在一起,形成了一件复杂而错综复杂的艺术作品,突出了霍金森的创新思维和创造力的变革力量。
这艘迷人的莫比乌斯船在印第安纳波利斯艺术博物馆展出,是该地区任何人的必游之地。
它令人信服地证明了数学和艺术之间有趣的相互作用,以及如何以最意想不到的方式将抽象概念带入生活。

莫比乌斯船 by Tim Hawkinson丨印第安纳波利斯艺术博物馆
莫比乌斯带的影响也延伸到建筑领域,最著名的例子之一是阿斯塔纳的哈萨克斯坦国家图书馆。
图书馆由著名的丹麦建筑事务所BIG(Bjarke Ingels Group)设计,其结构灵感来自莫比乌斯带,创造了一个连续的内部和外部空间循环,无缝地相互流动。
这座建筑奇迹象征着知识的无限性,是收藏大量国家文学作品的图书馆的合适体现。
该设计非常出色,在国际竞赛中获得了一等奖,进一步强调了莫比乌斯带从艺术、数学到建筑领域的普遍影响。

哈萨克斯坦阿斯塔纳的国家图书馆 | 来源:ArchDaily
自然界中的莫比乌斯带
除了在艺术、数学和建筑方面的影响外,莫比乌斯带在自然界中也令人惊叹。
莫比乌斯拱门是在加利福尼亚州因约县的阿拉巴马山发现的一种非凡的自然形态,是莫比乌斯带在自然界中反映的另一个迷人例子。
这个壮观的岩石露头是一个主要的旅游景点,体现了莫比乌斯带的标志性扭曲,似乎无视传统几何学的规范。

莫比乌斯拱门 :加州阿拉巴马山丨尼尔·格罗斯科普夫
它最引人入胜的特征之一是其窗口状的光圈,巧妙地勾勒出美国本土最高的山峰惠特尼山的远景。
这种令人叹为观止的排列方式为全景景观增添了独特的维度,创造了数学奇迹与自然之美的和谐融合。
这个地理奇迹证明了莫比乌斯带无处不在的影响,不仅在数学和艺术的抽象世界中,而且在我们周围的有形世界中都展示了它的宏伟。
本文经授权转载自微信公众号“数学大院”,来源于Brilliant和维基百科
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 