数学是纯粹理性的象征。科学的很大一部分是以数学和逻辑为基础的。在某种意义上，数学就是理性的语言，它是所有人类发明中最成功的。然而正如我们即将看到的那样，就连数学也有自己的局限。
 

本文节选自《理性的边界》 第九章  数学面临的障碍

撰文 | [美] 诺桑·亚诺夫斯基

译者 | 王晨

1、写完这封信，就去捍卫爱情了

巴黎，1832 年 5 月 29 日。一名年轻的男子正在奋笔疾书。他必须快速写下这封长信，因为需要写的内容很多，而他知道自己第二天就会死于非命。

这封信是对他的数学研究的总结，他想在为时太晚之前将这些内容全部写在纸上。他在信的最后恳求他的朋友：“向（闻名世界的数学家）雅可比或高斯征求他们的公开意见，不是让他们判断这些定理的真实性，而是评价它们的重要性。我希望将来有人能够解开这团乱麻。”

第二天，他为了捍卫对一名女子的爱情而参加了一场决斗，结果正如他所料，他受了致命的重伤。被带到当地医院之后，他只活了一天。据说他最后的遗言是说给他哥哥的：“别哭，阿尔弗雷德！我需要我所有的勇气才能在 20 岁死去。”这个年轻人的名字是埃瓦里斯特·伽罗瓦（Évariste Galois，1811—1832），而他的工作将永远是现代数学的重要组成部分。

这封信里有什么？20 世纪最伟大的数学家和物理学家之一赫尔曼·外尔写道：“如果按照它所含信息的新颖性和深刻性来看，这封信或许是人类所有文献中最重要的著作。” 或许外尔在做这个评价时有些浮夸了，不过伽罗瓦的研究成果的确包含对现代数学和物理学至关重要的思想。一个 20 岁的年轻人能够说出什么重要的理论呢？

伽罗瓦出生于 1811 年，当时法国大革命之后的狂热气氛还没有散去，这让伽罗瓦度过了短暂而悲剧的一生。他的父亲曾经是巴黎郊外一个小城市的市长，后来因为一场激烈的政治争端而自杀。伽罗瓦是一个满怀激情且心思复杂的年轻人，他的成长过程很不容易。他很年轻的时候就痴迷于数学，以至于荒废了其他方面的学习。他没有考上法国最负盛名的巴黎综合理工学院（École Polytechnique），最终进入了一所第二梯队的大学，但老师并没有真正地发现他的聪明才智。伽罗瓦提交了两篇用来发表的论文，结果都被编辑弄丢了。后来他参与了激进的政治团体，导致自己被学校开除。目前还不清楚这次致命决斗的另一方是谁，引起决斗的女子的身份也未知。如果这位年轻的天才没有以这么悲惨的方式英年早逝，他还能完成什么样的工作呢？这个问题的答案只能靠猜测了。

伽罗瓦的工作和多项式方程的求解有关。在理解他的贡献之前，我们必须先研究一些历史。思考下面这个简单的方程：

ax + b = 0

此类方程称为“线性”方程，大多数中学生知道如何求 x：

x = –b/a 

更复杂的“二次”方程是下面的形式：

ax2 + bx + c = 0

古典时代的人们就已经知道了这种方程的求解方法，而且一直到现在，高中学生还在学习使用“二次公式”求二次方程的解。二次方程实际上有两个解：

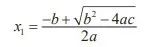
及
 

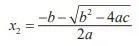
注意这些公式使用了加法、减法、乘法、除法、求平方和平方根等运算。那么“三次”方程呢？如下所示：

ax3 + bx2 + cx + d = 0

这种方程的求解存在标准公式吗？16 世纪，杰罗拉莫·卡尔达诺指出这个方程有三个解，而且给出了相当复杂的公式。这些公式使用了普通的运算方式，包括求平方根和立方根。继续下去，我们可以试着求解“四次”方程：

ax4 + bx3 + cx2 + dx + e = 0

洛多维科·费拉里（Lodovico Ferrari，1522-1565）和尼科洛·丰塔纳·塔尔塔利亚（Niccolò Fontana Tartaglia，1499-1557）发现了四次方程的解。你一定很想知道我们是否会写下这四个可能的解对应的四个公式。与其将它们写下来，不如说这些“四次公式”使用了普通的运算，包括求平方根、立方根和四次方根。那么“五次”方程呢？如下如示：

ax5 + bx4 + cx3 + dx2 + ex + f = 0

事情在这里变得更有趣了。也许有人会觉得存在由加减乘除和从平方根到五次方根组成的“五次公式”。这是不对的！不存在这样的公式。19 世纪初，保罗·鲁菲尼（Paolo Ruffini，1765-1822）和尼尔斯·亨利克·阿贝尔（Niels Henrik Abel，1802-1829）证明了不存在这种使用普通运算和求方根的普适公式。这意味着对于每个由a、b、c、d、e、f组成的五次方程，永远都不会存在简单的求解公式。这是数学局限性的又一个清晰的例子。一般而言，这个问题是不可解的。然而某些五次方程存在很容易找到的解。例如，x5 – 1 = 0 有一个解为 x = 1。

这就是伽罗瓦的工作重心。他能够使用某个给定五次方程的系数确定该方程能否用普通运算求解。为此，伽罗瓦引入了群（group）的概念。群是一种以对称概念为模型的数学结构。伽罗瓦指出了如何将一个群与每个方程关联起来。在这些对称性的帮助下，他能够判断某给定五次方程能否用普通运算求解。当他对五次方程求解的工作得到理解之后，就立即被用在数学和科学的许多其他领域。

这种描述对称性的概念涉及现代数学、化学和物理学的一次重大革命。现代数学和科学的很大一部分研究的是不同形式的对称性，因此也就是不同类型的群。从这个角度，我们终于可以理解外尔对伽罗瓦书信内容重要性的判断：现代数学和科学广泛地使用了伽罗瓦引入的观念。

如果要一五一十地介绍伽罗瓦理论（Galois theory）究竟是如何发挥作用的，我们一定会晕头转向。简要地介绍一下就足够了，这个理论首先描述了数学或物理系统的对称性。建立了这种对称性之后，研究人员就要确保这种对称性在不同运算或物理法则下得到保持。一个系统不能违反自身的对称性，这个事实可以看作对该系统的限制。

我们在 9.1 节见到的不可解决的古典尺规作图问题都可以使用伽罗瓦理论证明其不可解决。我们还没有讨论的另外一个问题是某些正多边形（regular polygon）是否可以用尺规作图构造。等边三角形和正方形是可构造的。正五边形呢？任意的正 n 边形呢？伽罗瓦理论告诉我们哪些正 n 边形可以使用尺规作图构造出来。所以如果

 n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, …, 257, … , 65 537, … 

那么与之相应的正 n 边形就是可构造的。相比之下，如果

 n = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, … 

那么这样的正 n 边形就是不可构造的。

伽罗瓦理论描述的这种限制性体现在一个很有趣的例子上，那就是经典的儿童游戏十五子棋。这个著名的益智游戏有 15 个小方块安装在一个 4×4 的网格里。每次可以移动一个方块，目标是让这些方块按顺序排列，如图 9-6 的右半部分所示。然而某些开局排列方式无法得到按顺序的排列方式。只要简单地交换一下编号为 14 和 15 的方块的位置，就无法得到按顺序的排列方式，也无法从按顺序的排列方式恢复到最初的排列方式。

实际上这些方块可能的排列方式一共有 15 的阶乘（15!）种。这些方式中正好有一半称为“偶排列”（even permutation），而另一半称为“奇排列”（odd permutation）。方块普通形式的移动有一种对称性，只能从偶排列变成偶排列，或从奇排列变成奇排列。这些现象体现了该系统的对称性。在图 9-6 中，一种排列方式是偶排列，而另一种是奇排列。

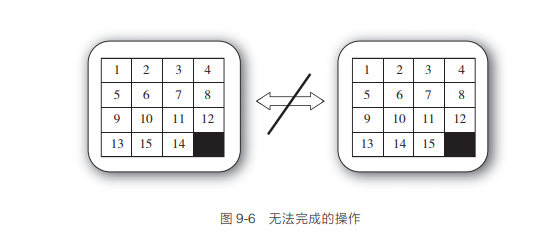
正是因为这个事实，所以无论我们进行多少次规则范围内的移动，都无法将一种排列方式变成另一种。

还可以在魔方上看出与伽罗瓦理论有关的不可能性。拿出一个完全拼好的魔方，然后只扭动它的一个角（尽管这违反规则）。将它打乱，然后让一个观察力不佳的朋友（没看过本书的朋友）试着拼回原状。这是不可能完成的。一次扭动就让它无法恢复原状，无论用多少步骤也不行。

总之，伽罗瓦的方程理论指出了乘法、除法、乘方和求方根等普通运算在方程求解中固有的局限性。多年以来，数学家开发出了使用微积分和无穷方法的其他技术，解决了这些问题的一部分。所以伽罗瓦理论证明了某些问题无法用特定方式解决。与之类似，如果允许使用直尺测量确切的长度，那么所有正 n 边形都可以构造出来。对于十五子棋游戏，只要将所有棋子都拿出来，再按照正确的顺序摆回去就很容易解决问题。通过作弊的方式总能解决魔方问题，也就是将它一块块拆开，再按顺序拼装起来。这些都是绕过伽罗瓦描述的数学局限的简单招式。

2

计算机永远无法解决的判定问题

假设你找到了一份工作，是在某个建筑承包商手下打工，帮助客户设计他们梦想中的厨房。本来一切顺利，直到某个百万富翁的妻子走进来，想更换厨房的地板。她不想要样式普通的方砖，而想别出心裁地使用圆形的砖。你向她指出圆形的砖没法用，因为会留下无法填充的缝隙，如图 9-7 所示。

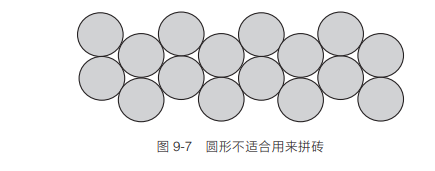
正五边形适合吗（见图 9-8）？

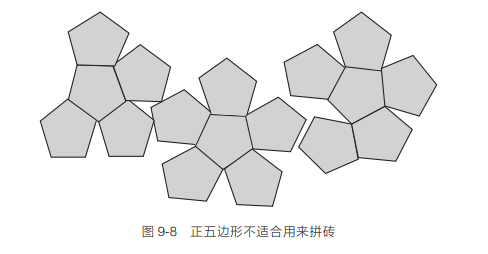
正五边形也不适合，但你没有放弃，又向她提议使用正六边形，如图9-9 所示。
 

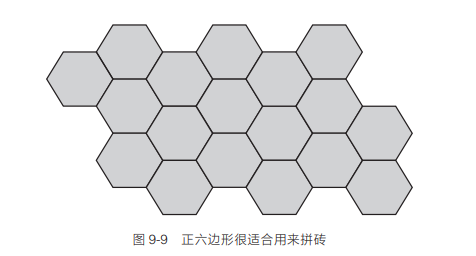
这次没有空隙了。正六边形可以用来给地板拼砖。可以看出，有些形状适合无缝拼接，有些形状不适合。图 9-10 展示了其他两种只使用一种形状的拼接方法。
 

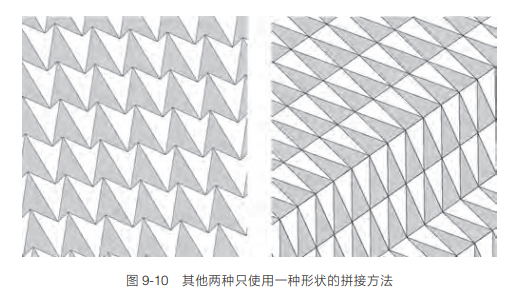
很显然还有许多其他形状可以严丝合缝地拼接起来。闻名世界的荷兰画家M. C. 埃舍尔（M. C. Escher，1898-1972）制作了一些精彩的蚀刻版画，他将这些奇怪的形状彼此拼接在一起，不留一丁点儿缝隙。

思考图 9-11 中称为迈尔斯图形（Myers shape）的怪异形状。

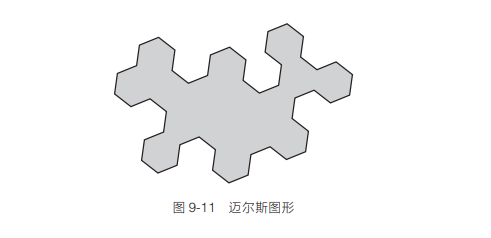
有人也许会觉得形状如此奇怪的拼块不可能不留缝隙地覆盖地板。但是它完全可以做到这一点。如图 9-12 所示，一点儿问题也没有。

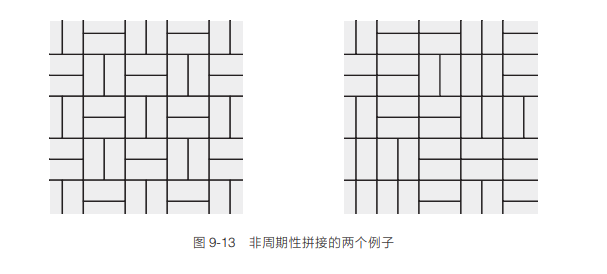
我们见到的大多数形状在拼接时使用的方法会让拼接出来的图案自我重复。这种拼接方式被称为具有周期性。在周期性拼接中，同样的图案一次又一次地出现。然而某些形状拥有不存在重复图案的拼接方式。这种拼接方式被称为具有非周期性。思考长宽比为 2×1 的矩形。这个形状很容易创造周期性拼接。

然而我们也可以用这种矩形创造非周期性拼接。将两个这样的矩形拼在一起就得到了一个正方形，这种正方形可以垂直或水平放置，如图 9-13 所示。由于任何图案都可以像这样创造出来，因此创造非周期性拼接很容易。

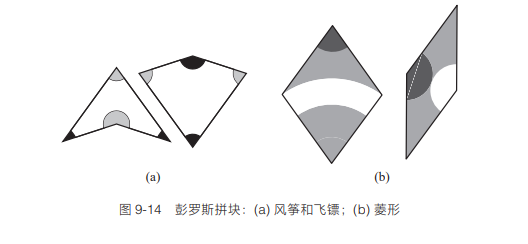
我们还可以在非周期性图案的问题上向前再走一步。存在某些形状的组合，当你用它们来拼接时，它们形成的图案永远不会是周期性的。换句话说，这些形状只能拼接出非周期性图案。因此，这些形状被称为非周期性拼块。罗杰·彭罗斯（Roger Penrose）发现了两组这样的形状，其中一组是“风筝”和“飞镖”，另一组叫作菱形（见图 9-14）。

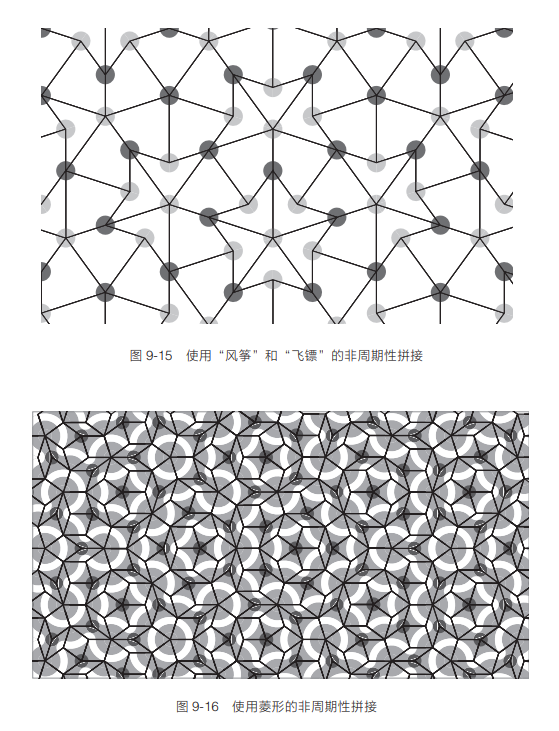
这些形状有不同的颜色。当这些形状的拼接方式令相同的颜色对接在一起时，形成的图案就不会是周期性的。图 9-15 和图 9-16 就是这种非周期性拼接的例子。
 

我们回到帮别人拼厨房地板砖的工作上。如果存在某种方式能将不同形状的组合输入一台计算机，让它告诉我们这些形状能否拼接成一块没有缝隙的大地板（不用考虑边缘问题），那就太妙了。我们将这个接受形状并判断它们是否适合拼接的任务称为拼接问题（tiling problem）。能够解决拼接问题的计算机会对圆形和正五边形回答“否”，对正方形、等边三角形、正六边形、迈尔斯图形、彭罗斯的“风筝”和“飞镖”以及彭罗斯的菱形回答“是”。这样的计算机程序对你的工作会有巨大的帮助。

可惜的是，这样的计算机程序不可能存在。20 世纪 60 年代中期，罗伯特·伯杰（Robert Berger）证明了不存在能够解决拼接问题的计算机程序。

他证明这一点的方法是指出这个问题比我们在第 6 章见到的停机问题还难。停机问题问的是某个计算机程序是最终停机还是陷入死循环。如我们所见，任何计算机都不可能解决停机问题。既然拼接问题更难，那么它也不能被任何计算机解决。

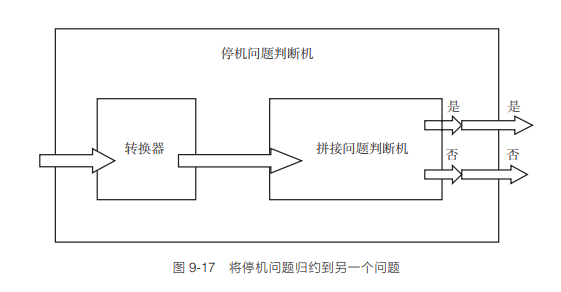
具体地说，可以将任何计算过程转换为一组形状，并使得当且仅当这些计算过程永不停机的时候，这些形状才能拼接出一个平面。也就是说这些形状能够拼接地板被等同于计算过程进入死循环。（我们在 6.3 节中见过这种转换过程。）可以用图 9-17 形象化地表示这种一个问题转换（或归约）为另一个问题的过程。

在这幅示意图中，一个程序从左侧进入，然后转换成一组形状。假设（错误地）存在一台计算机可以判断一组形状能否形成无缝拼接。那么我们就拥有一种方法可以判断某个程序是陷入死循环还是停机。由于我们已经知道没有任何方法能解决停机问题，因此我们就知道没有任何方法能解决拼接问题。

像拼接问题这样计算机永远无法解决的判定问题叫作不可判定问题（undecidable problem）。虽然这些问题有清晰的定义和客观存在的答案，但任何计算机永远都无法解决它们。

值得强调的是，我们证明拼接问题不可判定的方法是基于停机问题不可判定这个事实的。

停机问题可判定矛盾。

图 9-17 指出：

拼接问题可判定停机问题可判定。

将这两个蕴涵推导结合起来，我们得到拼接问题可判定矛盾。因此拼接问题不可判定。判断一组特定的形状能否用来拼接地板，这只是比停机问题难因而不可判定的众多问题之一，这样的问题还有很多很多。

本文经授权转载自微信公众号“图灵新知”。