时间晶体,这一曾有争议的理论如今正逐渐走向现实,而且在量子人工智能领域展现出巨大的应用潜力。它究竟如何与量子人工智能相结合,又能为我们带来什么新知?
撰文 | 尹璋琦
“时间晶体”是美国麻省理工学院物理系教授、诺贝尔物理奖获得者弗朗克·维尔切克(Frank Wilczek)于2012年提出的一个新颖的物态概念:一种物质,当其处于基态附近时,在时间维度上会自发出现周期性变化,就像空间晶体在空间维度上自发出现周期性重复一样。维尔切克写出这个定义后不久,在接受记者采访时大胆地发扬了想象力:未来有一天,随着技术的高度发展,我们可以对时空晶体进行编程,设计出复杂的周期运动回路,代表不同的比特,以及比特间的运算,然后把我们的人脑意识上传到这个时空晶体中。这种携带了人脑意识的时间晶体可以称之为时光胶囊。

图1:美国麻省理工学院物理系教授、诺贝尔物理奖获得者弗朗克·维尔切克(Frank Wilczek)
我读了报道后,也写下了浪漫的构想:“拥有了这样的时光胶囊,即使地老天荒,即使宇宙热寂,我们那些美妙的情感仍旧永存。把爱保留到宇宙尽头之后,也许会是我们研究制造时间晶体最浪漫的动机。”
当时,不论是维尔切克还是我,都觉得用时间晶体做计算机的设想遥不可及。没想到,这个浪漫的构想真有可能变为现实:我们最近发现时间晶体可以辅助实现高效量子机器学习算法,加速量子人工智能落地。时间晶体是如何跟量子人工智能结合起来的,请让我从头说起。
时间晶体构想:从备受争议到实验验证
2012年时间晶体构想提出后不久,很快引发巨大争议。转机出现在2016年,美国的Norman Yao等人提出离散时间晶体的概念:在周期性驱动的系统中存在时间平移自发对称性破缺,系统展现的周期与驱动周期之比为大于1的整数。比如外加驱动周期是T,而系统展现出的运动周期是2T。通常来说,量子多体系统受外加驱动时,很快就会吸收能量变为热平衡态,从而丢失初始状态所包含的信息,这个过程也被称为热化。而处于多体局域化的量子多体系统,由于多体局域化机制的保护,并不会吸收外加驱动的能量热化,而会长时间携带初态信息。这突破了时间晶体必须在系统基态中实现的原始定义,避免了理论上的争议。同时,由于对系统的初态也没有太多限制,多体局域化离散时间晶体很适合实验验证。
2017年,来自美国马里兰大学Christopher Monroe团队和哈佛大学的Mikhail Lukin团队各自独立的验证了离散时间晶体理论。但是实验的实现并不是争议的结束,而是新一轮争议的开始。人们开始讨论这些实验是不是真的能够避免热化,实验中是不是掺入了其它机制,比如说“预热化”:由于存在一些对称性和准守恒可观测量,其热化过程将会被抑制,从而为离散时间晶体行为的观测提供了时间窗口。预热化只能保护接近系统基态附近的低温动力学,与可以保护任意初态,近乎永远不热化的多体局域化量子时间晶体相比,仍显平庸。

图2:时间晶体概念图。
当学术界为此争论不休时,量子计算机从天而降,近乎完美的实现了多体局域化量子时间晶体。2021年,谷歌公司宣布,基于超导量子处理器实现了多体局域化量子时间晶体。如下图所示,谷歌团队使用链状的20个超导比特实现时间晶体,尺度变大后,尺寸效应与边界效应都可以忽略。他们使用数字化量子模拟来实现离散时间晶体哈密顿量,这比起以前的实验来说在参数上具有更大的可操控性。通过对各种初态进行实验,不仅展示了离散时间晶体的“倍周期”动力学,也验证了多体局域化不依赖于初态的特性。不仅如此,谷歌公司的工作还验证了离散时间晶体对系统哈密顿量参数和外加控制参数误差的鲁棒性:在很宽广的范围内,离散时间晶体物态都能稳定存在。
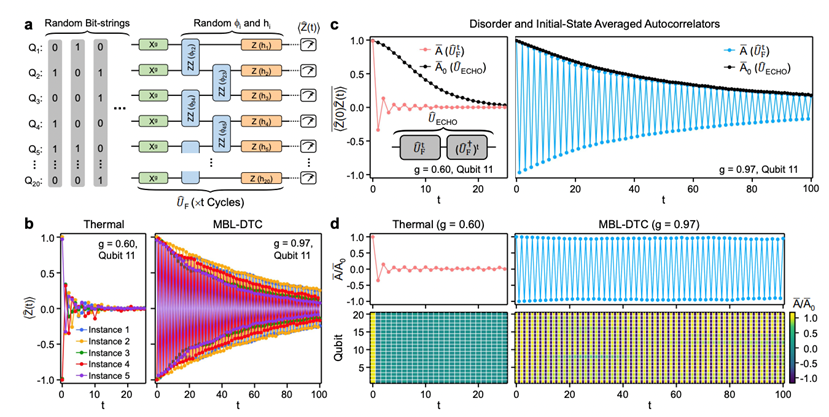
图3,谷歌公司离散时间晶体示意图(a)制造离散量子时间晶体的量子线路图;(b)热化与多体局域化离散时间晶体动力学比较;(c)对不同初态与失序参量取平均的离散时间晶体动力学;(d)利用自旋回波线路降噪之后获得的无消相干影响近乎完美的离散时间晶体。
时间晶体中的量子人工智能:从一个有趣想法开始
在谷歌公司验证离散量子时间晶体的同时,我们也跟中国科大量子计算团队合作尝试验证离散时间晶体。但由于实验条件的限制,这个工作并未达到最初的设计目标,只实现了衍生U(1)对称性保护的预热化相,没有验证离散时间晶体。谷歌公司离散量子时间晶体论文发表后,我马上让博士生李鑫跟进。他加入我组里已经三年多了,对数字量子模拟多体系统演化,以及用变分量子求解器来计算多体基态等方法都很熟悉。仔细研读谷歌公司论文后,他产生了一个很有趣的想法:既然离散时间晶体对控制参数具有很好的鲁棒性, 那么基于离散时间晶体的量子线路,是不是可以设计一个能调参的变分量子本征值求解器(VQE)。与机器学习类似,VQE一般是先定义一个代价函数E,然后调整随机量子线路的参数,使得代价函数E趋近于最小。但随着量子比特数增加,以及线路深度增大,调参时VQE代价函数的梯度迅速下降到趋近于零,出现所谓“贫瘠高原”现象,导致基于VQE的量子算法难以走向实用。基于离散时间晶体的量子线路进行调参,也许可以避免代价函数E的梯度迅速下降的问题。
李鑫跟我讨论这个想法之后,我也觉得很有前途,鼓励他尽快设计线路进行模拟验证。很快他就发现基于时间晶体线路的VQE调参,梯度不再下降,阻碍VQE算法实际应用的贫瘠高原现象也就消失了。离散时间晶体线路中的OTOC等指标与随机线路VQE中的OTOC也不一样。实际上,在离散时间晶体线路中,量子比特之间的量子纠缠增长相比随机线路方案较慢,这可能是避免“贫瘠高原”背后的原理。我们用海森堡模型作为例子,测试了用新的参数化线路计算基态能量的效率,发现相对随机线路的效率也有极大提升。我建议李鑫试试其它类型的离散时间晶体线路方案,关键是要弄清楚VQE算法效率的提升,到底是多体局域化带来的,还是离散时间平移对称性破缺带来的。
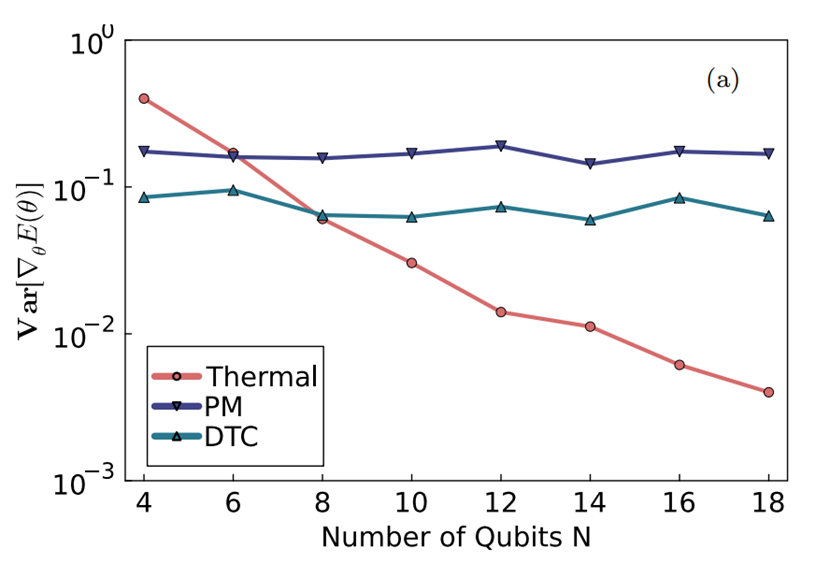
图4:多体局域化中存在的离散时间晶体(DTC)和顺磁相(PM)都可以避免梯度下降,而系统处于热化区时,VQE代价函数梯度随量子比特数指数下降。
如上图所示,我们确认,算法效率的提升主要是由于多体局域化,时间平移对称性的破缺不是最基本的,多体局域化才是算法有效的根源。如果把量子线路参数调整到热化区域,VQE代价函数的梯度下降就又会出现。这暗示我们说,多体局域化所具有的避免热化的特性使得我们设计的VQE算法代价函数避免了“贫瘠高原”。如果考虑量子线路中噪声的影响,利用多体局域化的离散时间晶体参数化线路仍会更稳定一些。不论如何,我们可参照离散时间晶体,构建更稳定高效的量子参数化线路。在这个线路中实现的量子机器学习算法,可谓是时间晶体中的量子人工智能。这个工作最近已通过审稿在线发表(Front. Phys. 20, 023202 (2025))。
量子机器学习:量子计算未来新方向?
通过这个工作,我对机器学习与量子计算有一些不成熟的思考。2024年诺贝尔物理奖给了人工智能,准确的说是Hopfield和Hinton,他们的工作都与经典统计物理密切相关。Hopfield网络源自统计物理Ising模型,而Hinton提出的玻尔兹曼机也与统计物理深度联系,在此基础上人们发展出今天的深度学习。

图5,2024年诺贝尔物理学奖授予John J.Hopfield和Geoffrey E.Hinton,以表彰他们“为利用人工神经网络进行机器学习做出的基础性发现和发明”。
把经典机器学习推广到量子机器学习,可能得把神经网络的底层逻辑从经典统计物理推广到量子统计和量子多体物理,从那里去找灵感,设计相应的量子神经网络和量子线路,供量子计算机发挥威力。我们把量子时间晶体模型用于VQE算法,取得了很好的效果,也许就是无意中找到了个例子。沿着此思路做下去,我们能把离散量子时间晶体理论用于更多的机器学习任务中,如图像识别、随机时序数据分析预测等。
本文经授权转载自微信公众号“墨子沙龙”。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 