阅读:0
听报道
创造⼒的来源是天真。你还记得自己在幼儿园时,将一个苹果和数字“1”联系起来,然后数着苹果计算“1+1=2”时遭遇的困惑吗?这种困惑或许并非偶然,我们接受的数学教育常常是抽象出概念而忽略具体差异的过程,但我们的思考方式却天⽣是范畴学的,它关注一个苹果和另一个苹果的不同,关注事物之间的相互关系。
在还原论和演⽣论角逐的今天,范畴学正变得越来越重要。可以说,微积分对还原论的物理有多重要,范畴学对演⽣论的物理就有多重要。范畴学带来了超乎数学家想象的波澜壮阔,它在概念上统⼀了分析和代数,统⼀了离散和连续。今天我们就带着曾经对 1+1=2 抱有的好奇⼼,进入范畴学的奇妙世界吧!
撰文 | 孔良(深圳量子科学与工程研究院,南方科技大学)
引 言
这篇⽂章真的是讲你在幼⼉园学的1+1=2,不需要任何数学背景也可以读,只需要你有对1+1=2的好奇⼼。但是我们的动机却是要介绍数学⾥⾯的范畴学的基本精神,所以有必要先简单提⼀下范畴学,不关⼼的读者可以直接跳过引⾔。
范畴学起源于代数拓扑,由Samuel Eilenberg(1913-1998)和Saunders Mac Lane(1909-2005)于上个世纪40年代提出。⾃从六⼗年代Alexander Grothendieck (1928-2014)⽤范畴学的语⾔重建了代数⼏何基础以来,数学中就出现了⽤范畴学替代集合论作为数学的新基础的潮流。这个潮流不但在数学⾥⾯愈演愈烈,还在90年代被注⼊了新的强⼤动⼒:物理。
⼈们发现描述二维有理共形量⼦场论和任意维拓扑序的数学语⾔也是范畴学。当然这也没有什么奇怪的,了解范畴学的⼈都不会惊讶。因为范畴学带来的变⾰是如此底层,它从根本上改变了我们看待数学(甚⾄是其他学科)的基本范式。⽽不了解范畴学的⼈可能会对这句话有很⼤的抵触。这个也是正常的,没有真正了解范畴学,会很难想象范畴学是可能的,也许看完此⽂,你的抵触会稍稍减少⼀些。
我认为范畴学是继⽜顿的微积分⾰命之后,⼜⼀次语⾔的⾰命,其实范畴学本身就是⼀个新的微积分。她的⼒量体现在许多⽅⾯,⽐如:⼀个简单的范畴学的公式就可以完成⼀个复杂的量⼦场论的构造,或同时计算⽆穷多量⼦场论的融合 (fusion) ;很多复杂的物理和数学结构⾃然⽽然就是范畴学的;更重要的是,很多超越集合论的数学或物理事实只能在范畴学的意义下陈述和理解。仅仅是最后⼀条就告诉我们,有⼀个集合论之外的数学新⼤陆等我们去发现、去探索。现在还有更疯狂的猜测,那就是范畴学是多体量⼦纠缠和量⼦引⼒的基础。
范畴学的变⾰是如此底层,它会毫⽆疑问地在⼏乎所有科学领域发挥作⽤,包括逻辑学、数学、物理、计算机科学、语⾔学、社会学、经济学等等。所以让更多数学以外的⼈了解它是有意义的。本⽂就抛砖引⽟地讲讲,这个变⾰是如何的底层,底层到需要我们不断地回归,直到每⼀个⼈开始数学启蒙的那⼀刻。
一 1 + 1 = 2 ?
我相信我们每⼀个⼈的数学教育都是从1+1=2开始的,从那⼀刻开始,我们就开启了⼀场“去范畴化”的抽象数学之旅,⽽范畴学则是⼀场回归。
创造⼒的来源是天真。
-- Alexander Grothendieck
我希望⼤家和我⼀起回到学龄前⼉童的状态。只有这样你才能看清问题的本质。
1+1=2 是很难理解的。我们真正理解了吗?也许你觉得没有什么困难,但是只有当你给⼀个从来没有听过 1+1=2 的学龄前⼉童解释的时候,你才能明⽩这个问题有多么困难。
第⼀个难点是:什么是“1”?
第⼆个难点是:什么是“+”?
第三个难点是:什么是“=”?
第四个难点是:什么是“2”?
什么是“1”?你确定自己知道什么是“1”吗?你⻅过1吗?⼩朋友不知道什么是“1” 。为了让小朋友理解数字,通常情况下,⽼师的教法是⽤实物,⽐如⽤带磁铁的⼩猪、⼩鸭、苹果、⾹蕉等等,把它们吸到带⾦属的⿊板上。真实可⻅的东⻄才是我们对存在的基本体验,其他都不太可靠。
让我⽤符号 O 来表示苹果,J 来表示⾹蕉。我们再把⼏个苹果放到⼀起,于是⿊板上出现了如下公式:
O+O=OO, (1)
好吧。我们⻅过苹果,所以O没什么问题。但什么是“+”?什么是“=”呢?
其实⼩朋友⼀般还可以接受(1),接受的办法就是忽略“+”。(1)不就是 “OO=OO”吗?理解“+”是很难的。我先跳过,先来谈谈“=”,其实这个更难!
“=”(等于)是⼀个很难理解的东⻄。在现实世界⾥我们基本没有⻅过两个完全⼀样的东⻄。“OO=OO” 两边的苹果其实是不⼀样的。真实情况往往是,也许它们的颜⾊有些区别,或者磁铁的吸⼒有些差别,等等。那么“=” 就很难理解了。在⽣活⾥说中⽂时,我们不说等于,我们说“⼀样”。那么左边的“OO” 和右边的“OO”在什么意义下是“⼀样”的呢?
请让讲⼀个让我震惊的故事。我第⼀次在深圳中学做报告的时候,我说我不知道什么是“⼀样”,请中学⽣为我这样⼀个“学龄前⼉童”解释。然后有⼀位勇敢的同学上来,他分别从左边的OO和右边的OO ⾥⾯各拿出⼀个苹果,然后把这两个苹果放在⼀起,再把剩下的两个苹果放在⼀起,他说这个就是“⼀样”。事实上他给出了左边OO和右边OO的⼀个⼀⼀对应,可以⽤⼀个图来代表他的这个⼀⼀对应:
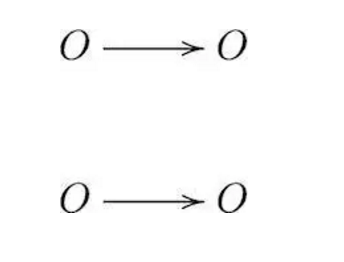
这个已经⾜够精彩了吧,但是精彩的还在后⾯。问题是你为什么要这么做?我们在学习⽣涯中就遇到很多的困惑,常常不清楚有些选择到底是有背后原理指导的,还是偶然的、随机的。其实孩⼦们是敏锐的。⼀定有看上去很“笨”的孩⼦会纳闷,为什么要这样?当时,这个同学解释完,我就问⼤家对这个“⼀样”的定义有何意⻅?然后就有很多学⽣对此发出质疑。⾸先,这样定义是不是⾃然的,合理的?其次,这样定义也不是唯⼀的,⽐如你还可以选择下⾯这个来定义“⼀样”:
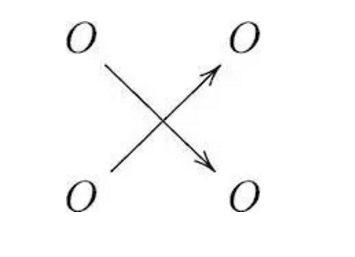
说句⽼实话,我当时震惊了,我藏在后⾯的东⻄全被中学⽣⾃⼰发现了。⼤家看出来问题是什么了吗?
真实世界里可能没有两个东⻄是完全⼀样的(请让我忽略量⼦⼒学⾥的全同粒⼦,我们现在在幼⼉园,没有听说量⼦⼒学)。⼀般⼤家要看两个东⻄⼀样不⼀样,就把这两个东⻄⽐较⼀下。但是这两个东⻄不可能完全⼀样,所以⽐较的时候要忽略⼀些属性,一个极端的情况是,我们忽略一个苹果的所有内部结构和属性,把它看成一个既没有内部结构也没有附加属性的东西(就是集合论里面的元素)。这种情况下,一一对应就是一个很好的“一样”的定义。如果我们接受了这样定义“⼀样”是可⾏的, 即⽤“⼀⼀对应”来定义“⼀样”。那么问题来了:
有两种不⼀样的“⼀样”还是⼀样吗?
现代数学或范畴学就是对这样⼀个基础的问题做了深刻的思考。现代数学或范畴学的观点是:有两种不⼀样的“⼀样”就是不⼀样,除⾮有⼀个⽐另⼀个更⾃然。⽐如:左边的苹果⼀个是红的,⼀个是绿的;右边也是⼀个红的,⼀个绿的。⼀个⾃然的“⼀样”是保持颜⾊的“⼀样”。但是在没有颜⾊这个附加“结构”之前,我们有两种不⼀样的“⼀样”,其实就是不⼀样。
为那些有线性代数基础的读者加⼀段:
这个问题看似简单,但是却是⼀个核⼼问题,在数学⾥⾯⼴泛出现,造成很多初学者的困惑。⽐如中国的不少教科书把线性代数教成了矩阵代数。很多学⽣⼀想到⼀个线性空间,就⾃动给它装上⼀个向量基。事实上,(线性空间+给定的基)是和线性空间完全不⼀样的数学结构!不明⽩这个就⽆法明⽩⼀个线性空间和它的对偶空间的区别,到了微分⼏何,也会困惑切空间和余切空间的区别。⼀个有限维线性空间和它的对偶空间有⽆数线性同构,但是没有⼀个是⾃然的!但是⼀个有限维线性空间到它的对偶空间的对偶空间有⼀个⾃然的同构。
我们注意到上⽂反复出现了“⾃然”这个词。⽽范畴学的起源,就是Ellenberg-Mac Lane试图定义什么是“⾃然”,由此引发了“⾃然变换” (natural transformation) 这个概念,为了定义“⾃然变换”,需要引⼊“函⼦“(functor)的概念,为了定义函⼦,⼜需要引⼊“范畴”(category)这个概念。
本⽂不想⾛进这些概念细节,但是我们希望能够展示⼀下范畴学的基本精神。粗略地说:所有苹果可以看成⼀个“范畴”,⽽所有⾹蕉是另⼀个“范畴”,它们都可以放到⼀个更⼤的叫“⽔果”的范畴⾥⾯。
我们想说,从OO抽象出来⼀个“2”的概念其实是⾮常困难的,⽽且往往需要很暴⼒的做法。⽼师在引⼊“2”之前,为了加深理解,还会再放两个⾹蕉。我们姑且⽤J来代表⾹蕉。于是⿊板上⼜出现了如下公式:
J + J = JJ, (2)
但是同样的问题仍然会令我们烦恼。更加令⼈困惑的是⽼师有的时候还要在⾛向“2”的路上做更多让我们困惑的事情,⽐如为了硬说这些都是“2”,还可能有这样的公式出现:
OO=JJ.
这样不在⼀个“范畴”能“⼀样”吗?甚⾄⼀不留神,⽐如苹果不够⽤了,可能临时还会出现下⾯的公式:
O + J = J + J.
疯掉了,苹果和⾹蕉能加吗?苹果和⾹蕉不在⼀个“范畴”怎么能加呢?事实上,我们可以说⼀个苹果是“1”,⼀个⾹蕉也是“1”,它们都是“1”的代表,但是从这些可以作为“1”的代表中抽象出来“1”这样的概念是⾮常困难的。也许那些连1+1=2都听不懂的孩⼦不是笨,⽽是把握住了⼀些深刻和本源的东⻄。
我们来看看范畴学怎么解读1+1。
二 范畴学的观点:万有性质
范畴学的观点就和我们最天真的看法⼀样,⼀个苹果是“1”,⼀个⾹蕉也是“1”。它们都是“1”的代表。既然只是代表,是不是说它们都还不是“1”?那么到底什么是“1”呢?
“1”应该反映出来所有这些“1”的不同代表所具有的“共有性质”。数学家给这个“共有性质”起了⼀个正式的名字叫“万有性质” (universal property) 。如何写下这些“1”的不同代表的共有性质呢?
范畴学提供了⼀种全新的视⻆。不要⽤“⼀个研究对象”⾥⾯“有什么东⻄”这样⾮常集合论或还原论的⽅式去看问题,⽽要以对象和其他对象的相互关系的⽅式来了解⼀个对象。这个⽅式其实是我们理解世界更根本的⽅法,⽐如你想了解⼀个未知的“存在”(如粒⼦、材料等),你怎么办?你会⽤你熟悉的东⻄打进去去看看会测量出来什么。物理学家会测⼀个新材料的发光谱和吸收谱,打X光进去看看X射线衍射;数学家会把球⾯扔进⼀个未知空间来测量,或看看能不能让⼀个群作⽤上去,等等。⾼能加速器的云室⾥⾯测的不是粒⼦的轨迹,⽽是粒⼦和其他东⻄相互作⽤的轨迹。没有相互作⽤,测量也⽆从谈起。可以⼗分安全地说:
这个世界上没有⽐相互关系或相互作⽤更基本的存在。
既然如此,我们可以尝试⽤相互关系来定义什么是“1”。
我们先回顾⼀个概念:集合之间的映射 (a map) 。集合就是⼀堆元素的“集合”,呵呵。不过值得指出的是,空集也是⼀个集合,就是⼀个没有元素的集合。那么什么是两个集合A和B之间的映射呢?⽐如考虑两个集合X={a,b}, Y={1,2,3}, ⼀个从X到Y的映射,记成
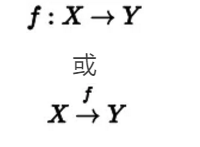
这其实就是⼀个分配规则:给X中的每⼀个元素分配唯⼀⼀个Y中的元素。⽐如,f(a)=1, f(b)=1 就是⼀个合理的映射, g(a)=2, g(b)=3 也是⼀个映射。但是不能给a分配两个Y中的元素!如果集合X⾥⾯没有元素(空集),等于分配规则⾃动定义好了,这个什么都不需要分配的分配规则就叫空映射。
有了这些准备,我们可以给出⼀下定义。

⼤家看到没有,这个定义⾥⾯⽤到了“1”和所有集合的关系,这件事相当重要。不过第⼀次看到这个读者可能更关⼼的是,为什么这是“1”的⼀个合理的定义呢?我们来看看,⼀个苹果的集合满不满⾜这个定义?⼀个⾹蕉的集合呢?或者,零个或三个⾹蕉呢,⼜或者所有中国⼈的集合?
如果你愿意尝试,你很快会发现,零个⾹蕉是不⾏的,因为它破坏了定义中映射“存在性”条件。“三个⾹蕉”也是不⾏的,因为它破坏了映射的“唯⼀性”。什么集合可以呢?就是那些只有⼀个元素的集合,⽐如⼀个苹果的集合、⼀个⾹蕉的集合、⼀个鸡蛋的集合、⼀个⼈的集合,等等,它们可以同时保证存在性和唯⼀性。
所以这样定义的“1”不唯⼀,这个好像是⼀个缺陷,但是妙的地⽅是,所有可能的“1”都有且仅有⼀种⽅式互相对应起来,这是由“存在性”和“唯⼀性”决定的,和“1”的具体内容⽆关。就像教⼩朋友时,可以⽤⼀个苹果代表1,也可以⽤⼀个⾹蕉代表1,⽽且我们知道如何把它们等同起来! 你能相信吗,幼⼉园虽然很努⼒地教“去范畴化”的数学,但教的⽅法是⽆法回避的范畴学!因为这就是它的本来⾯⽬。
⽽这个定义也被称为“1”的“万有性质”。也就是说,我们⽤“1”的性质来定义“1”,⽽不是⽤“1”⾥⾯有什么东⻄来定义“1”。所有的数学概念都可以⽤它的“万有性质”来定义,我说的是“所有”,是的,你没有听错!
好极了,如果你还能跟上我,我们就再来⼀个。
定义:0就是这样⼀个集合,它到任何⼀个集合都存在且有唯⼀⼀个映射。即对任意集合X,我们有:
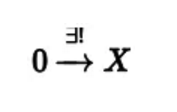
这个留给⼤家做练习吧。——科普还要留作业?没听说过,呵呵。不过想明⽩了这个习题,⻢上就福利了,可以⽴⻢去摧残⼩朋友和她们的⽗⺟啊。哈哈。
三 范畴学怎么解读 1+1 ?
好了,真正的挑战或摧残来了,我们终于可以看看什么是1+1了。和“1”⼀样,“1+1”也会有很多不同的代表,⽐如,2个苹果或2个⾹蕉,等等。那么“1+1”应该是什么呢?应该是所有这些代表所拥有的共性,即万有性质。下⾯我们就来揭示“1+1”的万有性质。我先擦擦汗。


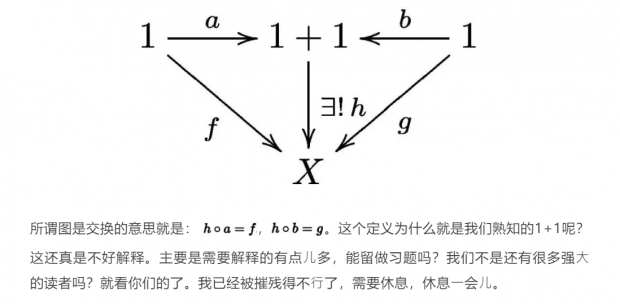

我想指出的是:
(1)虽然我们没有规定a和b必须是什么,但是万有性质导致了a和b不能任意选。不同的a 和 b且满⾜万有性质的选择将被视为不同的1+1的代表!也就是说定义1+1需要有三个东⻄:(1+1, a, b)。
(2)满⾜1+1的定义的集合是不唯⼀的(都是代表),但是存在性和唯⼀性使得,它们任意两个代表之间都有唯⼀的⼀种⽅式⼀⼀对应起来。这⼀点相当的重要,但是我不是很想展开来说,可能也需要读者中的达⼈来解读。
(3)万有性质的另⼀奇妙的地⽅是,它不但定义了概念,还告诉你它是怎么⽤的,就是⽤来构造那个存在唯一的箭头!⽽且这是唯⼀的⽤法!这⼀点⼤概没有⽤过的⼈是很难体会的。这个集定义与应⽤于⼀身的特点也强烈证明了这是⼀个好的定义。
作业1: 我们到底是定义了2还是定义了“+”?
作业2:1 + 1 + 1 咋定义?
作业3:1 x 1咋定义?(提示:把定义1+1的那个图的箭头都反过来)。
作业3相当有意思,箭头都反过来就可以了?其实这也就是在说,乘法是加法的对偶概念。范畴学⽜逼的地⽅是说,数学⾥的所有概念都是这样的!数学⾥的所有概念只有两种:⼀种叫做“极限”(⽐如1 x 1),⼀种叫“余极限”(⽐如1+1)。其他没了。呵呵。所以范畴学把数学中的所有概念都放在了⼀个统⼀的框架⾥⾯来看。
众位看官可能要纳闷,这个怎么能叫“极限”呢?极限不是⼀个⽆限的(逼近)过程吗?事实上,⼤家熟悉的所谓“极限”不过是⽤⼀个有⽆限节点的交换图,并以和1+1 或1 x 1同样的⽅式来定义的概念⽽已。⽐如,对任意构成如下图的实数X,我们有:
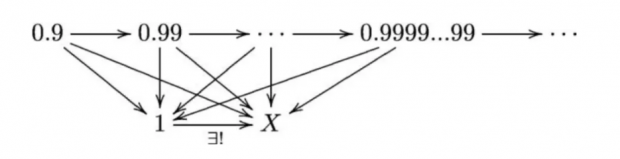
其中“1”是通常意义下的⼀个实数(不要理解成集合),箭头的意思就是“≤ ” (⼩于等于)(不是集合之间的映射!)。这个图说的是,⼀个序列:0.9, 0.99, 0.999, ... 的极限是1。⽤范畴学的语⾔说就是1是图表 0.9→0.99→0.999→... 的余极限。
怎么看呢?X是这样的⼀个实数,序列 0.9, 0.99, 0.999, ...中的每⼀个数到X都有⼀个箭头,意思是说,序列 0.9, 0.99, 0.999, ...中的每⼀个都 ≤ X 。⽽1就是这样的⼀个数,⽽且是最⼩的那⼀个,对吧?
所以范畴学是⾃动包含你熟悉的微积分的,但是她能做更多!事实上范畴学在概念上统⼀了分析和代数,统⼀了离散和连续,1+1和传统意义上的极限没有本质的区别,不过是涉及的交换图有⼤有⼩⽽已。
作业4: 如果箭头的意思改成“ ≥ ”,相当于上图的箭头都反过来。则在范畴学的意义下,我们得到“1”是⼀个图表的极限。
另外你应该还注意到,范畴学中的箭头可以不是映射,可以是任意可能的关系。⽐如“≤ ”,再⽐如,在所有中国⼈构成的范畴⾥⾯,我和你本没有关系,但是如果我们都追同⼀个⼥孩⼦,这样我们就有了情敌的关系,这也可以是范畴学中所研究的相互关系。这个例⼦还可以想象,可很多时候,在范畴学中出现的所谓“相互关系”是千奇百怪的,甚⾄是超越想象⼒的。
四 范畴学、物理和计算
我想⼀定有⼈觉得快发疯了,1+1搞的这么复杂。我想强调的是,这个故事并不是“复杂”,⽽是1+1的本来⾯⽬。不过读者也可以反对说,“去范畴化”才是真的有⽤,1+1搞的这么复杂的话,没法⼦⽅便地计算了。所以这样理解1+1,就算是本来⾯⽬,怎么可能有⽤呢?
这样定义的1+1确实有些复杂,并不实⽤,但这是⽤⽜⼑去杀鸡,当然就看不到它的⼒量了,⽜⼑⽜在可以通杀⼀切众⽣。其实范畴学是研究⽆穷维数学结构的强⼤⼯具,在那⾥她的⼒量就能够真正地显露出来。⽐如在研究量⼦多体系统的时候,有能隙的量⼦多体系统的边界和内部的关系可以由下⾯这个万有性质来定义[2]。
这图啥意思?啥意思不重要。重要的是,你发现没有,⼀个具有⽆穷⾃由度的复杂物理系统,边界和内部的关系竟然没有⽐1+1和1的关系更复杂!这是因为范畴学有能⼒把有限维的数学和⽆限维的数学统⼀在同⼀个框架下处理。值得⼀提的是,上⾯图表揭示的关系也同时刻画了弦论⾥⾯开弦和闭弦的对偶!这些都是⽆穷维数学结构之间的对偶。如果真的把对偶两边的数学结构⽤⽣成元和它们的关系写下来,会复杂得吓死⼈的。呵呵。
在演⽣论 PK 还原论的今天,范畴学越来越重要。这是因为范畴学就是为演⽣论准备的。你看看“1+1”难道不是从所有集合中演⽣的概念吗?同理,所有数学概念都是在包含⼀定意义下的“所有”对象的图表中演⽣的对象。甚⾄范畴学强调要放弃还原论的观点,不要问⼀个集合⾥⾯的元素,⽽要去看映射,后者更加丰富。⽐如,⼀个集合X ⾥⾯的⼀个元素其实就是1到X的⼀个映射!
这样的观点难道不就是加速器的原理吗?想知道粒⼦⾥⾯有什么东⻄,就拿其他东⻄,甚⾄是“它”⾃⼰,去轰“它”。我想微积分对还原论的物理有多重要,范畴学对演⽣论的物理就有多重要。范畴学和物理学家理解⼤⾃然的基本⽅法和原理是完全相合的,她们都强调:
没有⽐相互关系或相互作⽤更基本的存在,其他都是演⽣的。
范畴学和物理的关系当然值得⼤书特书,很多最前沿的论⽂都在不断地讲述这个关系。这⾥我们点到为⽌,虽意犹未尽,只盼能抛砖引⽟,诱发⼤家的兴趣。
如果说范畴学在数学⾥很基本,那么在物理或其他学科⾥⾯是不是也应该很基本?现实是,在物理中⽤的上范畴学的可能只是很少的⼏个⾮常小众的课题。这是为什么呢?这是暂时的还是⻓久的?范畴学会带来描述物理学的新的微积分吗?范畴学对未来的计算机科学会有何影响?希望将来我们有机会来解读这些问题。
你们喜欢范畴学吗?欢迎⼤家来到范畴学的奇妙世界。
附录
⽂章结尾我们来谈谈学习范畴学的过程中常⻅的困惑和误解。
很多⼈(包括部分数学家)都抱怨范畴学抽象。我希望前⾯的讨论能够帮助⼤家意识到,我们的思考天⽣就是范畴学的,⽽引⼊“1”和“2”这样的抽象概念反⽽是“去范畴化”了。我们的数学教育从⼀开始就是“去范畴化”,⽽通常的微积分可以看作是“去范畴化”的经典之作。最终的结果是,我们⼤多数⼈第⼀次学“范畴学”都会觉得好“抽象”,呵呵。有可能是因为 “去范畴化”的数学教育让我们变得失去童真了。
我记得有⼀次在做数学报告,有听众抱怨范畴学太抽象了。我说,抽象是⼀个没有意义的概念,不过你所谓的不抽象的东⻄是啥?他回答说⽐如上同调。我的天,上同调不抽象?好吧,我耐⼼地问,为什么你觉得上同调不抽象?他说,因为可以算啊。我说,原来可以算就是不抽象啊,这样的话,范畴学也不抽象,因为它也可以算。但是这也不重要,因为这个说法本身很荒唐,如果上同调是可以算的话,总没有1+1=2更好算吧?那么请问什么是“1”?平时我们嘴上说的所谓“不抽象”或“抽象”,其实就是“熟悉”或“不熟悉”。范畴学之所以显得“抽象”,就是因为我们在“去范畴化”的路上⾛了很远了,想要回归也没有那么容易,放下包袱是很难的。
我记得有⼀次和物理学家Michael Levin吃午饭,他说他花不少时间看范畴学,但是总觉得范畴学空泛的好像什么都没有。他的感觉没错,当然也不只他⼀个⼈这样抱怨。事实上,范畴学是和集合论⼀样底层的东⻄。就象你去看集合论⼀样,除了⼀些形式的定义,仿佛什么都没有。
对物理学家来讲,看集合论⼏乎没有任何⽤处,真正有⽤的是微积分和线性代数。所以也只有当你看到了范畴学⾃⼰的“微积分”和“线性代数”的时候,你才能理解它的强⼤。我认为,Grothendieck的代数⼏何就可以粗略地看成是⼀个新的“微积分”,⽽张量范畴理论 (tensor category theory) 可以看成是⼀个新的“线性代数”。范畴学⾥⾯的“微积分”(或“线性代数”)都不是唯⼀的,⽽是千变万化的。对物理学最有⽤的“微积分”和“线性代数”可能还没有诞⽣。
与集合论不同的是,对物理学家来说,集合论可以完全地忽略,直接跳到微积分和线性代数上,因为集合论的语⾔和基础被函数论的语⾔覆盖了。但是对范畴学来讲,想要跳过她的基础语⾔:范畴、函⼦、⾃然变换、Yoneda引理,直接学习她的“微积分”和“线性代数”是不可能的。遗憾的是,到⽬前为⽌,还没有⼀个适合物理学家读的范畴学的书。
还有⼀种误解是,范畴学已经建⽴好了,学好了⼀本范畴学的数学书,在物理上的应⽤可能就够了。如果你抱着这样的⼼态,那你注定要失望了。⾸先,把任何(不论她有多么优美)数学套⽤到物理上的想法都是缘⽊求⻥的做法。只有从物理实验或物理图像出发⽽发现的数学才是对物理有意义的,如果碰巧这个数学已经被数学家发现,那也只是偶然情况⽽已。通向未知之⻔⼤多是没有现成的钥匙的。
物理学真正需要的范畴学绝⼤多数还不存在,需要我们去⼀边发展物理,⼀边发展数学。在这种情况⾥⾯,新的物理和新的数学没有区别,它们都是⼤⾃然的隐藏结构。现在的范畴学还在发展的初级阶段,微积分可以发展⼏百年的话,范畴学⼤概也需要⼏百年。⽽我这些年的实践告诉我,物理能给我们带来的新的、超越数学家想象⼒的范畴学才是真的波澜壮阔。
致谢
感谢德国哥廷根⼤学的朱晨畅⽼师、清华⼤学⾼等研究院的汪忠⽼师和丘成桐数学中⼼的⽥垠⽼师、南科⼤量⼦科学与⼯程研究院的吴咏时⽼师和郑浩⽼师、麻省理⼯学院的⽂⼩刚⽼师、中科院物理所的曹则贤⽼师和斯坦福⼤学的祁晓亮⽼师提出的很多宝贵意⻅。
注释
[1] 这⾥⾯我们还是⽤到了“唯⼀”这个概念,好像是循环定义“1”的意思。其实我们可以从技术上回避它,⽐如:我们可以说万有性质中的(让图表交换的)映射构成的集合存在到集合{O}的双射。
我们这⾥并不是想探讨数学的基础,⽽是展现⼀种对1和1+1的全新解读。不过从万有性质⾥⾯不断地⽤“存在”和“唯⼀”可以看出,在⾃然哲学的意义下,“唯⼀”有可能是和“存在”同等基本的概念。
[2] Boundary-bulk relation in topological orders, Liang Kong, Xiao-Gang Wen, Hao Zheng, Nucl. Phys. B 922 (2017), 62-76 [arXiv:1702.00673]
版权说明:欢迎个人转发,任何形式的媒体或机构未经授权,不得转载和摘编。转载授权请在「返朴」微信公众号内联系后台。
话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 