撰文 | 孟子杨

来源 | 本文选自《物理》2021年第7期

 

十四行诗，英文叫Sonnet，老一辈翻译家还曾根据音译翻成商籁体，很好听。其实是欧洲的格律诗，最初是小诗、小歌谣，也不一定十四行，随着历史的演进十四行诗句的格式逐渐被定型下来，而且押韵结构也有了严格的限制。在文艺复兴时的意大利，有了彼特拉克体 (Petrarchan Sonnet)，音韵优美，以歌颂爱情为主。一般分为两部分，前一部分由两段四行诗组成，韵脚为a-b-b-a，a-b-b-a；后一部分由两段三行诗组成，韵脚为c-d-e，c-d-e。后来流传到英国，莎士比亚创作了大量的十四行诗 (其十四行诗集收录154首，是莎翁全部作品中的重要一部分)，内容也从描写爱情扩展到更加广泛的领域，结构变成了三段四句加最后两句，一般的韵脚为a-b-a-b，c-d-c-d，e-f-e-f，g-g，是为莎士比亚体 (Shakespearean Sonnet)。我们来举一个实际的例子，下面是著名的莎翁十四行诗第18篇 (Sonnet 18)：Shall I compare thee to a summer′s day? (我能否将你比作夏天？)。

 

Shall I compare thee to a summer′s day?

 

Shall I compare thee to a summer′s day?  (a)

Thou art more lovely and more temperate：(b)

Rough winds do shake the darling buds of May，(a)

And summer′s lease hath all too short a date；(b)

 

Sometime too hot the eye of heaven shines，(c)

And often is his gold complexion dimmed；(d)

And every fair from fair sometime declines，(c)

By chance, or nature′s changing course untrimmed：(d)

 

But thy eternal summer shall not fade，(e)

Nor lose possession of that fair thou ow′st；(f)

Nor shall Death brag thou wander′st in his shade，(e)

When in eternal lines to time thou grow′st：(f)

 

So long as men can breathe, or eyes can see，(g)

So long lives this, and this gives life to thee. (g)

 

我能否将你比作夏天？

 

我能否将你比作夏天？

你比夏天更加美丽温婉。

狂风将五月的蓓蕾凋残，

夏日的勾留何其短暂？

 

休恋那丽日当空，

转眼会云雾迷蒙。

休叹那百花凋零，

摧折于无常的天命。

 

唯有你永恒的夏日常新，

你的美亦将毫发无损。

死神也无缘将你幽闭，

你在我永恒的诗中长存。

 

只要一天有人类，或人有眼睛，

这诗将长存，并赐给你生命。

 

韵脚在每句后标明，大家可以反复咀嚼体会，其实和中国的格律诗还有点模糊的相似。下面的中文翻译是笔者从市面上几家中凑出来的，尽量兼顾信和达，但还不够雅，仅供参考。

 

虽然字面上还是写爱情，如诗人将爱人比作夏天，寓意美丽和生命力的茂盛，但是也说出了夏天的不完美，也有狂风、骄阳、阴暗和结束的时候。任何美丽都会时过境迁，然而只要诗歌可以流传，诗中的美——人类的精神创造，就可以在时间的长河里不朽。这就超出了原本十四行诗只是情歌的范畴，讨论起人的价值和人类创造的意义，从卿卿我我鸳鸯蝴蝶走向了人文主义的命题，是现代人的觉醒。

 

莎翁身后，十四行诗大行其道，一如老杜开创的律诗道路对中国后世诗人的影响。弥尔顿、华兹华斯、雪莱、济慈、勃朗宁夫人，还有俄国的普希金、莱蒙托夫都创作出优秀的十四行诗，以至于普希金的诗体小说《叶甫盖尼·奥涅金》就是用十四行的格律写成，小说由四百多个十四行诗的单元组成，人称“奥涅金诗节”，前无古人后无来者，一如战斗民族在其他领域 (比如物理学) 中的做事风格。

 

到了近代、现代，作为格律诗的十四行诗就像中国的律诗绝句一样，慢慢被白话的自由体诗歌替代。但是还是有人创作不懈，如德语诗人里尔克和俄国的阿赫玛托娃都有传世之作，而且他们描写的也是更加深沉和广阔的主题，如前者的《致奥尔甫斯的十四行诗》(前后两部共55首) 与后者的《海滨的十四行诗》。而正是里尔克的作品，对中国新诗人产生了极大的影响，这也就让我们散漫的叙述又落到了中国，落到现代诗人、德国文学研究学者冯至身上。

 

1940—1941年间，诗人冯至经过了德国留学、回国工作，于抗战中辗转到昆明西南联大教书。他从1920年代新文化运动时期的浅草社、晨钟社，“我的寂寞是一条蛇”这样略显稚嫩的苦闷象征中蜕化出来。在经历了动荡年代的洗涤和近十年的沉默和思考之后，人到中年的诗人突然间被深沉的情感所唤起，爆发般地写出了27首十四行诗，就是有名的《十四行集》。除了具有同时期宣传爱国、痛诉苦难的作品 (如艾青、何其芳等人的) 的内容之外，冯至写出一些更高的、更普遍也因此更动人的感受，所以就算撇开时代背景，在今天仍会触动到我们内心深处的情感。这是诗人诗歌创作的巅峰之作，甚至可以说是“二十世纪上半叶中国诗歌创作的顶峰”。《十四行集》是冯至对生命的解答，而他给出的解答归根结底是两个字：孤独。他用雕塑般的语言，用沉静质朴的时空感受，完成了从幼嫩的白话诗到明晰的现代汉语诗的过渡。他的语言是适当欧化的白话，表现出具有现代性的感受力。不再啰嗦，还是抄一首做例子吧 (好在不用翻译了)：

 

鼠尾草

我常常想到人的一生，

便不由得要向你祈祷。

你一丛白茸茸的小草

不曾辜负了一个名称

 

但你躲避着一切名称，

过一个渺小的生活，

不辜负高贵和洁白，

默默地成就你的死生。

 

一切的形容、一切喧嚣

到你身边，有的就凋落，

有的化成了你的静默：

 

这是你伟大的骄傲

却在你的否定里完成。

我向你祈祷，为了人生。

 

这确实是现代汉语诗的高峰，不是古代的、也不是西洋的，而是新的、成熟的，描写着现代人的情感和困惑的中文。

 

其实拉拉杂杂写到此处，还没有触到这篇散漫文章的主题。也许这篇本来就没有主题，就像冯至的十四行诗，“但愿这些诗象一面风旗，把住一些把不住的事体”，只是在描述感受。那么就让我们按着如此的路数，接着描述笔者最近一段时间在量子多体纠缠中类似的感受吧。

 

诸君也许记得，我们在前文中讨论过纠缠熵的秋裤量法 (参见：量子多体中的呐喊与彷徨之八：我爱纠缠如秋裤. 物理，2021，50(3)：199) 。但量子多体晶格模型纠缠的定量测量，还是一个新的领域。其背后的内容牵涉到量子纠缠应该用怎样的数学语言来描述，怎样在晶格模型中有效地进行计算，既关乎数学物理理论的进步也涉及量子多体计算技术的发展，需要两相配合，才能达到有效探测量子多体纠缠这种与数学、物理学和信息科学都有关的新问题。

 

 

其中的一个主要想法，就是把量子多体系统放到有各种不同拓扑性质的流形上，然后把问题的配分函数和物理量在不同的时空流形上计算出来 (比如秋裤流形就是为了计算2阶Renyi纠缠熵所设计的)，然后分析计算所得到系统的物理性质，比如纠缠熵随着系统边界面积的变化形式，从而得到纠缠熵的面积律和更加重要的——面积率后面的对数修正项和常数项。对数修正项的系数，或者常数项的数值，就反映了我们关心的量子多体系统的一些隐秘的但更加本质的性质。

 

如我们在前文中介绍的，在具有自旋旋转对称性自发破缺的反铁磁奈尔态中，纠缠熵对数修正项前面的系数，就是系统中无能隙的戈德斯通 (Goldstone) 模式 (此处就是自旋波) 的数目 (图1)；而在量子临界点上的纠缠熵对数修正项的系数，就是如此相变共形场论描述中的中心荷 (central charge) 的值……纠缠熵的测量结果抓住了这些基本性质，就是抓住了如是量子多体系统的本质，超越了不同模型、不同量子材料繁复的化学、物理性质的表象。也正是因为能够让人们穿透量子多体系统指数增长的复杂性迷雾直抵问题的本质，纠缠熵——还有前文提到的无序算符等非局域测量——才吸引大家展开不懈的追寻。人们渴望能够建立量子多体纠缠的内部结构——也就是大家经常看到的拓扑序这一个名称——和流形的拓扑结构之间更加明确的关系，然后再通过切实可行的解析、数值计算方法，希望在量子多体晶格模型和更加复杂的实际材料中，把握纠缠，“把住一些把不住的事体”。

 

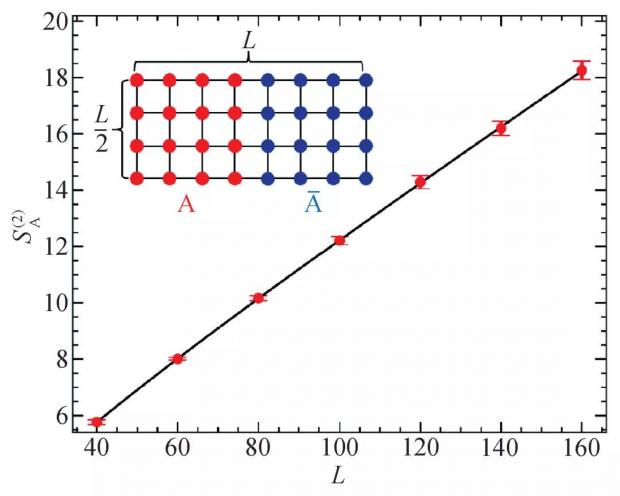
图1 二维正方晶格反铁磁海森伯模型2阶Renyi纠缠熵的量子蒙特卡洛秋裤计算结果。系统的几何结构如插图所示，子系统A与其补集之间的边界长度就是L。拟合计算所得的结果，可得纠缠熵对数修正项的系数收敛到Ng=2(拟合结果为2.0(1)，括号中为拟合误差)，这正是反铁磁的奈尔态中应该具有的 Goldstone modes 数目。此图为赵家瑞同学完善纠缠熵秋裤算法的成果之一，感兴趣的读者可以和前文“量子多体中的呐喊与彷徨之八：我爱纠缠如秋裤”中图3的数据相对照，数据质量、晶格尺寸都有显著提高

 

 

既然说到了拓扑序，那么我们就接着讲讲秋裤算法 (就是把量子多体模型的配分函数放到如秋裤一样的流形上进行计算的方法) 测量拓扑序的例子吧。其实我们早已知道，从实际的量子多体晶格模型出发 (不是严格可解模型)，是可以构造具有最简单Z2拓扑序的系统的，这样的晶格模型系统具有Z2量子自旋液体基态。如图2中插图里面的笼目 (kagomé) 晶格，人们其实早就写下了在如此晶格上自旋1/2的阻挫磁体模型，然后通过大规模的量子蒙特卡洛计算，给出了这样的模型在不同磁性相互作用强度、磁场和温度下的基态相图和低能自旋激发谱 (可以参考笔者的旧作：寂静春天里的动力学. 物理，2019，48(2)：104)，已经看到了这样的Z2量子自旋液体中的分数化任意子激发(spinon和vison) 在谱学和量子相变上的迹象。

 

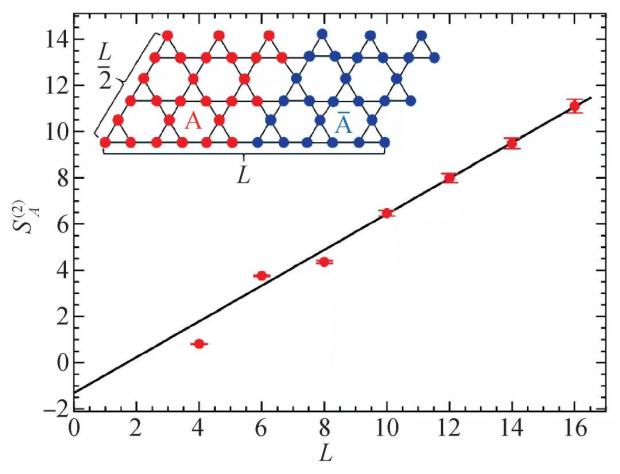
图2 kagomé晶格Z2量子自旋液体模型，二阶Renyi纠缠熵的蒙特卡洛秋裤算法结果。晶格中子系统的划分如插图所示，两个子系统之间的边界(就是纠缠熵面积律中的面积)就是L。随着模拟晶格尺寸的增大，纠缠熵满足“面积律(正比于L)+常数”的标度行为，那么当L足够大时，纠缠熵收敛到一根随着L增长的直线，就是图中黑线，收敛后的直线反推回在y轴上的截距，就是那个ln(4)=2ln(2)~1.4(2)的常数(括号中为拟合误差)。这个常数就反映了Z2拓扑序在二维周期性边界条件晶格流形下的4重基态拓扑简并度。拜秋裤算法所赐，这样的结果是第一次被准确得到。此图为赵家瑞同学完善纠缠熵秋裤算法的成果之二

 

那么如果问一下，描述这个简单的拓扑序系统的纠缠熵，或者更直接的，纠缠熵中的那个常数项，也就是描述Z2拓扑序在二维周期性晶格模型中的四重基态拓扑简并那个ln(4)=2ln(2)的常数项，有没有被看到过呢？此事说起来就不那么容易了，之前人们的确进行了十分努力的尝试，奈何纠缠熵的计算本身是一个十分困难的事情，之前最好的结果，也没有能够看到这个2ln(2)，至多看到了比ln(2)大一点的常数，再往下算 (就是增大晶格尺寸和降低温度)，彼时的算法还不完善，数据就被误差所淹没了。

 

也只是在最近，事情才有了进展，笔者和合作者完善了纠缠熵的非平衡秋裤算法，通过引入非平衡做功的介观物理概念和并行计算的程序实现 (细节此处从略了，解释以待来日吧)，终于可以在有限的计算资源下比较可靠地得到2阶Renyi在复杂的2维量子多体模型中的有限尺度标度关系，这是具有通用性的数值计算方法。

 

我们把如此的方法运用到kagomé晶格Z2量子自旋液体模型的蒙特卡洛计算中，得到了如图2所示的结果。我们把晶格划分为两个子系统，两个子系统之间的边界 (就是纠缠熵面积律中的面积) 就是L。随着模拟晶格尺寸的增大，纠缠熵满足“面积律(正比于L)+常数”的标度行为。当L足够大时，纠缠熵收敛到一根随着L增长的直线，收敛后的直线反推回在y轴上的截距，就是此处那个ln(4) = 2ln(2)~1.4的常数。之前的类似工作，只能勉强算到L=8 (也就是有3×8×8=192个自旋的kagomé模型)，而且误差已经很大。我们这里通过秋裤算法，可以准确、快速地把计算推到L=16，而且误差很小。这样就真切地看到了纠缠熵的收敛 (也回答了为什么之前L=8的计算无法给出确定性结果，因为如图2所示，L=8的时候，纠缠熵刚刚开始进入收敛区)，而通过收敛的纠缠熵再做线性拟合 (即图中的黑色直线)，直线在y轴上的截距就是准确的 ln(4) = 2ln(2)~1.4(2)，括号中为拟合误差，这个常数就反映了Z2拓扑序量子自旋液体态在二维周期性边界条件晶格流形下的4重基态拓扑简并度。拜秋裤算法所赐，这样的结果还是第一次被准确得到。

 

写到此处，请允许笔者在本文中做最后一次跑题，跑回到十四行诗。冯至的《十四行集》中的最后一首“从一片泛滥无形的水里” (不再抄了，感兴趣的读者可以自行查阅) 中有这样的话，“但愿这些诗象一面风旗，把住一些把不住的事体”。现代人的生活、我们面对的周边和世界，纷繁芜杂，又每每对我们施以略显荒谬的挫折和羁绊，让孤独的个体常常感到苦闷、迷惑和看不懂生活的本质，一如孤独的物理学者面对着现代的量子多体系统。但话说回来，我们这些渺小的个体仍想尽一己之力抓住一些生命中本质性的东西，能够把自己的思、想安排在一个暂且稳定的流形之上，就是哲人们所说的——在存在与时间中诗意地栖居。从这个意义上讲，从纠缠熵中看到对数修正的普适系数，看到拓扑序的普适简并度，就和冯至的十四行诗一样，让我们从泛滥无形的水里得到一个定形，用文字、用数学、用物理学、用计算，把住了一些把不住的事体。

 

 

本文经授权转载自微信公众号“中国物理学会期刊网”。