数世纪以来，不管对科学家还是对工程师，对数表都是非常实用的工具。现在，因与指数函数的密切联系，对数仍充满了极强的数学吸引力。

撰文 | 理查德·埃尔威斯（Richard Elwes）

翻译 | 齐瑞红、房超、于幻

在过去的很多年中，很多人习惯地把对数表放在手边用来帮助自己进行乘法和除法运算。在20世纪后半叶，便携计算器最终将对数表推入历史。但是，在级数和微积分的深层数学领域中，那引人入胜的发现确保了对数本身永不过时。

在16世纪后期，约翰·纳皮尔（John Napier）开始研究他最初称为“人造数”的数。他发现了一种方法，可以将复杂的乘法运算转化为相当简单的加法运算。为了求两个数的乘积，如4587和1962，他首先计算这两个数的人造数并求它们的和。然后将这两个人造数的和进行反人造数运算，即计算原数使得它的人造数就是这个和。虽然这个过程没有涉及乘法运算，但所得的结果确实是原来那两个数的乘积——8 999 694。

地震仪用来测量地震的强度。衡量地震强度的、国际上通用的里氏震级表正是对数运算：测定为3 级的地震强度是测定为2级的地震强度的10倍。

纳皮尔的对数

不久后，纳皮尔给他的人造数起了一个新的、更好的名字——对数。今天，我们明白对数只是幂运算的逆运算。幂运算指某数与它本身重复相乘，所以，“2的3次方”指3个2相乘，即2×2×2=8，也可写作23=8。相应地，我们说“以2为底，8的对数是3”，记作log28=3 。可以以任何数为底数来取对数，例如：以10为底，1000的对数是3（因为10×10×10=103）。对于纳皮尔的乘法，整个计算过程需要确定一个底数。所以，计算8乘以64的积，先以2为底取对数，分别得到3和6，对这两个对数求和：3+6=9。最后一步是对数的计算过程的逆运算，即计算29=512（可以核查8×64=512）。

布里格斯的对数表

在约翰·纳皮尔发明对数后不久，亨利·布里格斯（Henry Briggs）开始把它转变成一个有用的工具。因为我们应用十进制数制来表示数，布里格斯选择以10为底计算对数是比较方便的，并开始着手制作一个“对数表” ——从1到1000 的所有整数的对数。在几年时间里，布里格斯和其他数学家将这个表推广到一个更大的数集上。
 

当然，对于大部分整数来说，它们的对数都不是整数，所以研究者不得不给出他们求得的对数的精确程度。在18世纪后期，加斯帕德·德普罗尼（Gaspard de Prony）监督制作了一个特殊的数学用表，这个数学用表多达17大本双开卷，包括最大到200 000的正整数的对数，精确到小数点后第19位（对于较大的数，精确到第24位）。

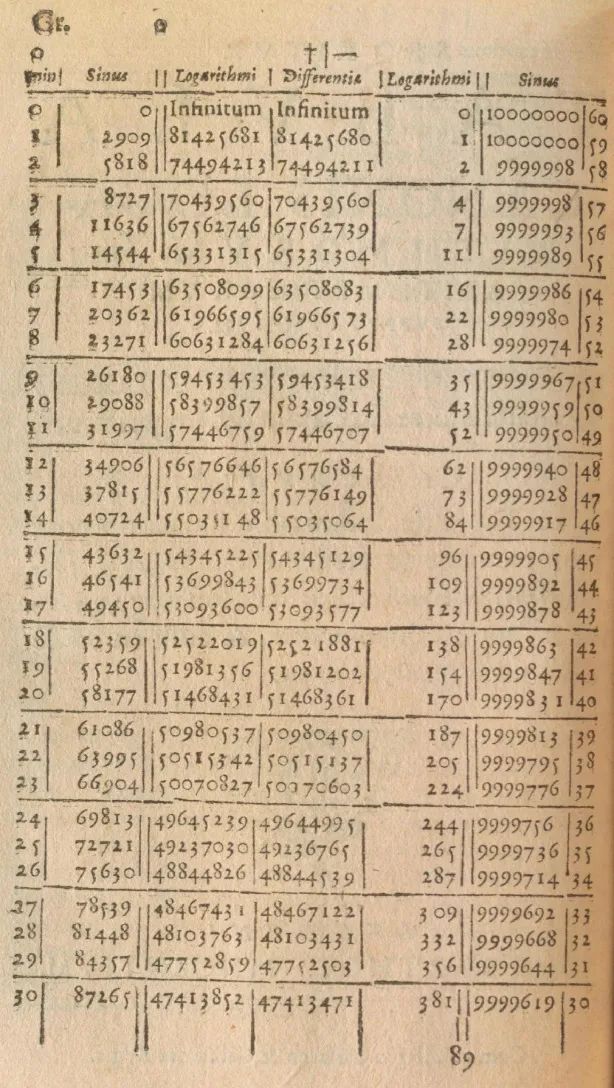
取自约翰·纳皮尔 1614 年的专著《奇妙的对数表的描述》里用的一张最早的对数表。约翰·纳皮尔研究的是后来被称为“自然对数”的对数，而亨利·布里格斯研究的是以10为底的对数——后来被称为“常用对数” 。

自然对数

自从纳皮尔发现对数以来，对数学家来说对数非常有用。就像杰出的科学家皮埃尔-西蒙·拉普拉斯（Pierre-Simon Laplace）所说的：“对数的发现通过节省劳动使天文学家的寿命翻倍。”但是，对数的数学意义比它作为计算工具的意义更为重要和深远。在1650年，皮耶特罗·曼戈里（Pietro Mengoli）首次意识到这一点。他的有关级数的研究与他在对数方面的兴趣出乎意料地结合在一起。
 

调和级数的表达式是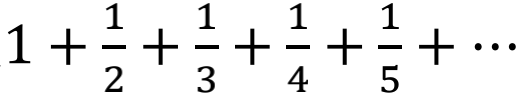。曼戈里有些吃惊地注意到这个表达式不趋近任何一个有限数，而是没有上限地不断增大。可是，若对它稍做修改，得到的另一个表达式1-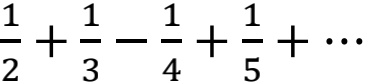收敛于一个固定的有限数。

这个交错级数有一个确定的极限，约等于0.693147。曼戈里证明了这个极限数就是 2 的自然对数（通常记作In2，虽然读成log2）。自然对数像其他的任何对数一样，只是对底数有一个特殊选择，以e为底数，e约等于 2.71828。确实，正是通过自然对数和曼戈里的结论，数学中最重要的函数之一——指数函数，开始崭露头角。

的确，对更准确的对数表的寻找有力地推动了抽象级数理论的发展。在1668年，尼古拉斯·墨卡托（Nikolaus Mercator）出版了名为《对数技术》的著作， 在此著作中，他发现了自然对数的级数公式：

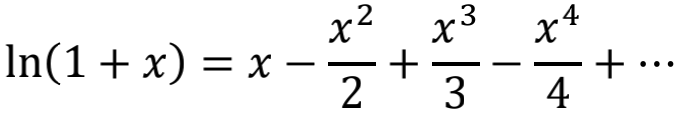这个美丽的定理正是曼戈里结果的推广，曼戈里的结果对应于x=1的特殊情形。

微积分和对数

墨卡托的定理暗示了自然对数的“自然”，但是一个更完整的故事需要用牛顿和莱布尼茨的微积分理论来诉说。

方程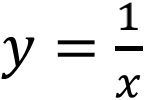描述了一个被称为“倒数”的重要概念。正是这个方程把2和½、4和¼ 、一百万和一百万分之一等联系起来。从几何图形上看，它是一条被称为“双曲线”的曲线。出乎意料的是，“自然对数作为这条曲线下方的面积”的说法出现了。这也是对数函数是指数函数的逆函数的这一事实的一个结论。由此可得自然对数y=Inx的导数只能是函数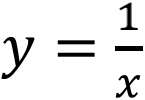。虽然现在对数表已被计算机所取代，但是这一深刻的事实确保了对数仍在数学中扮演着一个重要角色。

本文经授权摘自《图解数学简史：数学世界中不可不知的100个重大突破》第26篇《对数》。