用数学和物理学从本质上描述我们的大脑构造可能是一项不可能完成的任务,那么我们真的无法了解大脑吗?在神经科学方面,曾经轰动全球的“蓝脑计划”虽然至今未能复制大脑,但科学家重建了部分大鼠的模型,而数学家发现,拓扑学在了解神经元组成的网络方面,起到了神奇的作用。
撰文 | Rachel Thomas
翻译 | 张和持
2021年6月,欧洲数学大会(ECM)在斯洛文尼亚召开。在开幕第一天的最后,Betül Tanbay(土耳其著名数学家)向大家介绍了洛桑联邦理工学院 (EPFL) Kathryn Hess 教授的讲座:“通向复杂大脑的神秘数学之旅”。而当天的第一场演讲则是关于心脏的数学模型。这真可谓是用数学的方式紧紧抓住了听众们的“心灵”。Hess的旅程精彩非凡,这篇文章便是来分享她的奇思妙想的。
降 维
我们的大脑是由数百亿个神经元,以及用来连接神经元的数万亿个突触组成的网络,其复杂程度我们根本无法想象。如果再考虑神经元的形状、大小、朝向和一些其他因素,如大脑中的各层血管,情况还会更加复杂。Kathryn Hess 谈道,“为了避免直接处理如此复杂的对象,我们使用了一种数学家们都很熟悉的技巧。”
这个技巧叫作降维(dimension reduction),也就是说,选取具有代表性的简化信息。Hess解释说,其实我们每个人都会下意识地进行这样的操作。假如你到斯洛文尼亚参加这场大会,要从酒店前往大会会场,你想知道如何在这两点间的导航。并不需要知道周围的建筑是什么颜色,或者这些屋子里住的人都叫什么名字。你只需要知道什么时候左转,什么时候右转,以及每次转向之间间隔的距离。你可以想象是从导航地图的卫星视图(显示各种细节)切换成街道视图(只显示与交通有关的信息)。

Hess通过降维的方法,把大脑中如一团乱麻的神经元,表示为一幅网络图。每个神经元,暂且不论其形状与大小,全都表示为一个节点。节点之间的边则表示连接神经元的突触,不过即便两点之间有很多突触,也只表示为一条边(在真实的大脑中,这种冗余的突触数量被认为很重要)。由于信息沿突触传递的方向是一定的(从一个神经元的轴突到另一个神经元的树突),所以这些边都是有向的——由箭头表示信息传递的方向。两节点间有两条相反的边也是有可能存在的,就是指有相反方向的两个突触连接两个神经元。这个有向网络提供了大脑功能的简化结构。
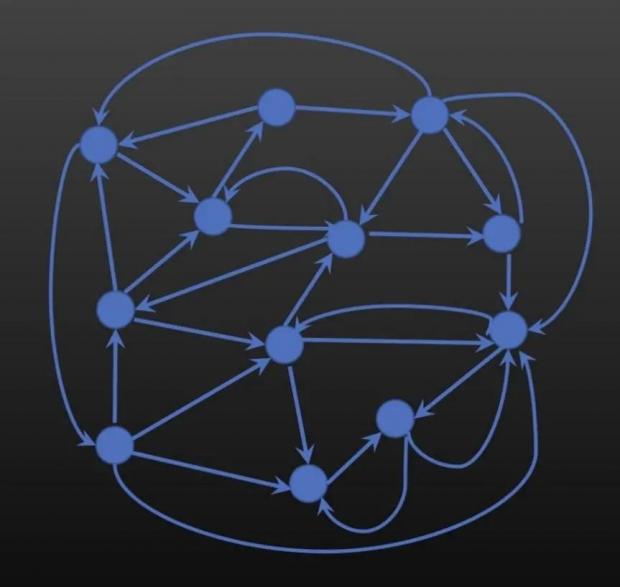
神经元网络可以用有向图来表示丨图片来源:Kathryn Hess
重建大脑
Hess与“蓝脑计划(Blue Brain Project)”进行合作。“(仿真)人脑模型的规模远远超过了我们力所能及,”Hess说道,“毕竟有数百亿个神经元,数据量是无法想象的庞大。”所以为了重建大脑的数学模型,“蓝脑计划”研究了比人类小得多的大鼠的大脑。不过Hess表示,即便鼠脑已经很小了,他们面对的仍然是“神经元网络的狂野纠缠”。
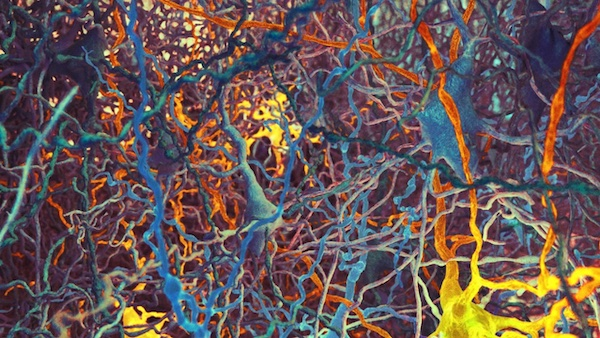
大鼠新皮层中不同类型的神经元缠结的数据可视化图像丨图片来源:Nicolas Antille, EPFL.
在过去的十年中,“蓝脑计划”重建了鼠脑中的躯体感觉新皮质(somatosensory neocortex)——这就像是从鼠脑表面深入到灰质提取出来一份岩心样本。大脑中负责触觉的部分组成一个微型电路,这里包括了大约30000个神经元以及它们之间的800万个连接。重建的过程,首先是在微型电路的柱状区域中安放不同的“神经元”,来模拟实验室中观察到的种类和数量。接下来这些神经元将按照邻近关系以及我们对鼠脑已有的信息来连接。
用来重建微型电路的算法包含了随机性(stochastic)。也就是说,算法中的某些分支是依照概率来选择的,所以算法每运行一次,重建的结果都会不同。“蓝脑计划”最开始使用的数据来自五块不同鼠脑,和一个汇集了各个大脑数据的“平均”脑。接着他们对每个数据集运行了7次重建(7次之间的差别其实不是很大),这样就有了总共42个微型电路。
之后,研究人员将突触的电性质编码到微型电路里,如此神经元电路就被真正连接起来,这样部分鼠脑的重建就完成了。“蓝脑计划”的最终目标是用重建的大脑来研究神经系统的失调,比如帕金森氏症,以及减少药物研发过程中的动物实验。
揭示结构
拓扑学是数学中研究形状分类的学科。如果某个图形可以通过弯曲或拉伸变成另一个图形,只要变化过程中没有切断或撕裂,我们就认为两个图形相同。最著名的例子就是甜甜圈和咖啡杯,它们从拓扑意义上来说是一样的。如果有一个橡皮泥做的咖啡杯,那么你只要把杯身一点点地往杯把的那边挤,就可以把它连续地变成甜甜圈。在这个变换过程中,咖啡杯把手的那个洞始终没有变,只是变成了甜甜圈的那个洞——洞是不可能消失的。拓扑学对于像洞一样,在连续变换下不变的量,非常感兴趣。
拓扑学提供了形状和连接性质的数学语言,它还可以用局部约束来描述整体结构。“拓扑学是绝妙的数学过滤器,”Hess讲解道,拓扑可以用来检测重建电路的结构以及连接性质,帮助人们理清各部分在大脑功能中扮演的角色。
对于如何将拓扑这个过滤器应用于重建的微型电路及其31000个节点,800万个连接上,Hess介绍了多种方法。她与同事所采用的方法是考虑能反映原网络显著特征的子网络。信息的流向在神经回路中至关重要,所以他们着重研究前馈子网络,这是指网络中的信息只沿一条路径传递。
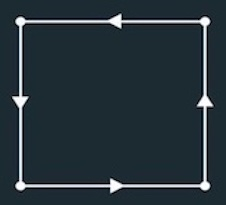
从拓扑的角度来说,这种结构可以用有向单纯形(Directed simplex)来表示。单纯形是三角形在任意维度下的推广:0-单纯形是一个点(节点);1-单纯形是一条线(节点之间的边);2-单纯形是我们熟悉的三角形(三个节点和三条边);4-单纯形是四面体(四个节点和六条边),等等。如果只考虑边有向的单纯形,那么一个前馈网络就可以由一个单纯形表示,而且这个单纯形中,方向指向完全向外的节点(网络的输入端),以及指向全向内的节点(网络的输出端)都只有一个。

不同维度的有向单纯形丨图片来源:Kathryn Hess
拓扑学的强大之处在于,即便只给出局部信息(例如这些神经元的连接方式),也能告诉你网络整体的重要特征。Hess和她的同事计算了神经元电路中每个维度中有向单纯形的个数,并将其与其他可比较类型的的网络进行了局部结构对应数量的比较。
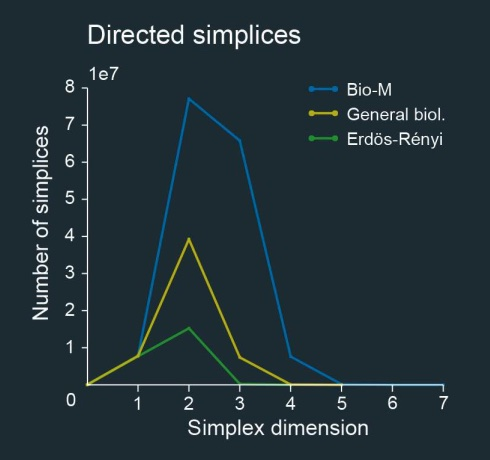
不同维度下的单纯形数量,蓝色代表“蓝脑计划”的微型电路;绿色代表随机网络;黄色代表更为一般的生物网络。图片来源:Kathryn Hess
他们构造了一种随机网络(图中的绿线),从任何一组数量相近的结点开始,随机地往外连线,使网络中边的数量保持一定,连接每个节点的边数也保持一定,这与神经微电路相似。在这种网络中,有向单纯形的数量非常少,而且没有维数在4以上的单纯形。他们发现,在更为一般的生物网络中(不考虑神经元的形状大小),也存在这种现象。
重建出的神经元微型电路中,有向单纯形的数量却比其他网络中高得多,而且还包括高维有向单纯形。Hess表示,“蓝脑计划”中的微型电路有更多(数量),该电路与随机网络相去甚远。”他们的研究结果表示,为了使神经元必要的传导行为能够协调……这些神经元必须得属于一个更大的结构(例如这些高维单纯形)。
数数有多少个洞
让我们回到上面说的甜甜圈和咖啡杯,它们的共通之处在于都有一个洞。球面则不然,它没有洞,所以没办法平滑地(指不撕开或不切割。译者注:数学上平滑/光滑(smoothness)指的是任意阶可导,而拓扑中的变换应该说连续)变换成甜甜圈,所以球面和甜甜圈从拓扑意义上来说是不同的。而物体中洞的数量——称为亏格(genus)——是拓扑中非常重要的一个概念,因为它在平滑变换下是不变的。洞的形状和大小有可能会变,不过数量不会。
而与此相对应的是,网络中也有一个概念,叫作腔(cavity)。这是指多个单纯形,互相的节点重合在一起,形成的一个封闭对象。比如说你可以把一个由1-单纯形组成的腔(即2-腔)想象成一扇窗户(窗户的边就是1-单纯形),而2-单纯形组成的腔(即3-腔)想象成一个房间(墙壁就是2-单纯形)。
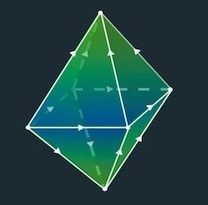
由8个2-单纯形构成的一个房间,或称3-腔。丨图片来源:Nicolas Antille, EPFL)
Hess解释说,“网络中的腔,是高度有序的,它们的存在揭示了网络的结构。” Hess和她的同事们计算了“蓝脑计划”的那42个不同微型电路中,不同维度的腔的数量。计算结果表明,这项拓扑参数忠实地反映了生物学事实。
下图展示了42个重建电路中,2-腔和3-腔的数量对比。不同颜色对应不同的大鼠(或者共用数据的平均鼠)。可以明显看出,同一只鼠的数据聚集在一起。对于不同鼠而言,上述拓扑参数显然是不同的,而对于同一只而言,又基本保持吻合。
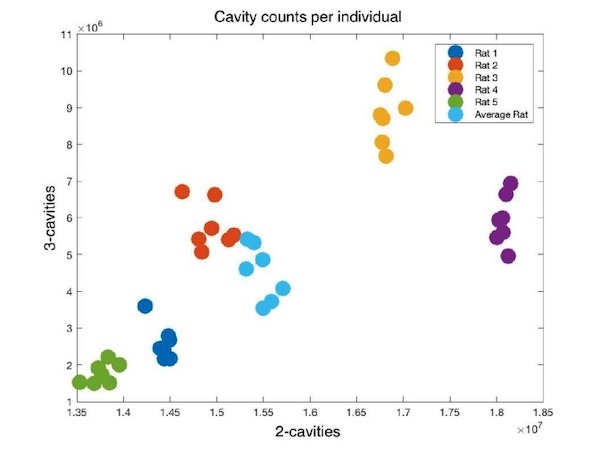
生物样本中拓扑参数的聚类分析丨图片来源::Kathryn Hess
有向单纯形和腔这两个数量参数,还可以用来分析神经网络中传递的电活动的波动。如果一条边对应的一个神经元正在触发另一个,则我们称这条边是激活的。研究者们可以用有生物学意义的时间步长,对每个步长内激活的单纯形和腔的数量进行计数,以此来观察活动的变化。下面这张图表——Hess和同事们称其为“嗖嗖(swoosh)”——展示了活动时数据沿曲线逆时针方向移动。
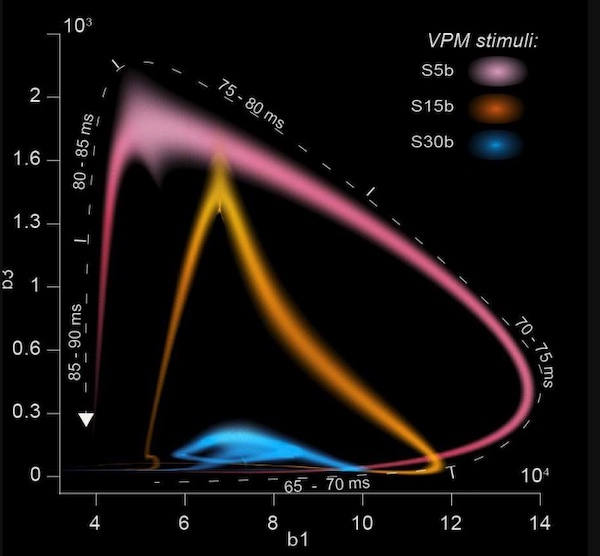
“嗖嗖”图展示了激活的3-腔(纵轴)与激活的1-腔(横轴)的数量丨图片来源: Kathryn Hess
Hess在她的演讲开头时说道,她职业生涯的前十年都致力于最纯粹的数学——拓扑、同调论和范畴论。现在她正在用同样纯粹的数学来研究大脑——正是大脑让我们有能力创造数学的奇思妙想。这又一次证明了数学在描述我们内在世界和外部世界方面都同样有效。
本文译自Rachel Thomas, The mathematical shapes in your brain
原文链接:https://plus.maths.org/content/mathematical-shapes-your-brain
0
推荐



 京公网安备 11010502034662号
京公网安备 11010502034662号 