机器学习工具已被用于辅助数学研究中通常依赖人类直觉和创造力的部分，并在两个不同的数学领域中各产生了重要结果。

撰文 | Christian Stump

自古以来，数学家会通过研究个例来提出新的理论。例如，观察过立方体和棱锥之后，人们会发现顶点数、边数和面数是相关联的。数学家辨认出这种规律后，将其推广到更普遍的形状，然后开始思考这种关系为什么可能成立。这个过程部分涉及计算，自从1960年代数学软件出现之后就在这方面派上了用场。但数学家得以直觉性地理解去哪里找规律是拜人类创造性所赐。在本期《自然》中，Davies等人描述了一种方法，使用人工智能（AI）技术辅助数学研究过程中的创造性核心[1]。

人们早在好几个世纪前就研究出凸多面体（表面为平面，棱为直线，顶点都向外凸出的三维形状）各个性质之间的关系了，描述这一关系的公式则得名于瑞士数学家莱昂哈德·欧拉。无论是哪种形状，顶点的数量（V）减去边的数量（E）再加面的数量（F）等于2：V-E+F=2（参见图1）。利用纸笔，你能通过几个不同的多面体个例得到这个公式吗？具体在这个定理上是可能的；但更复杂的数学思想就需要更大量的计算——而计算机在此极为有用。

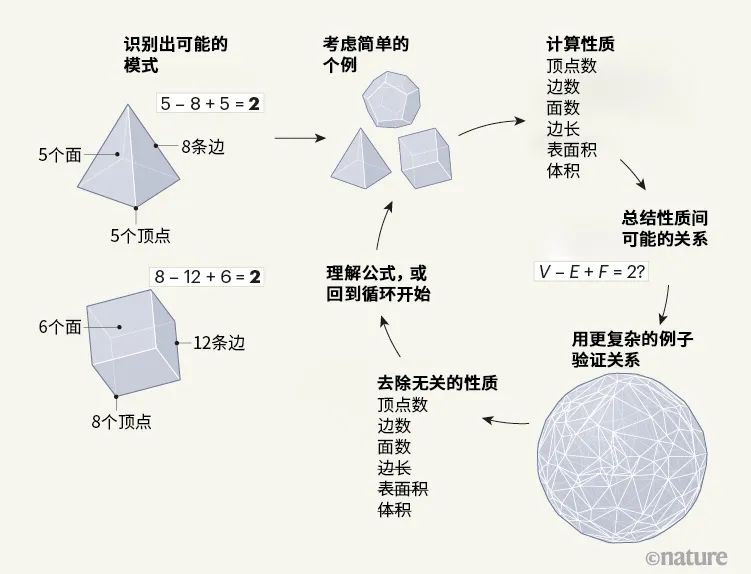
图1. 通过研究个例提出数学理论的循环。在识别出数学对象——例如凸多面体（表面为平面，棱为直线，顶点都向外凸出的三维形状）——性质中的一个可能模式之后，数学家一般会通过一个循环流程来理解这一模式。他们首先会计算一些简单个例的性质，并分析出这些性质之间可能的关系。研究者们接下来会总结这些关系。例如，他们总结出的可能是欧拉定理，凸多面体顶点数（V）减去边数（E）加上面数（F）等于2：V-E+F=2。然后他们会用更复杂的例子验证这一关系，去掉无关的性质，再试着理解该关系为什么成立。如果还是不清楚的话，数学家接下来会考虑不同的例子，从头开始循环。Davies等人[1]的文章说明了机器学习技术可以帮助研究者进行总结的步骤，而这一步通常极其依赖人类的直觉。

通过寻找和研究个例而进行的数学研究一般会遵循一种循环流程（参见图1）。首先，研究者找出几个相关的个例（立方体，棱锥，可能再加上十二面体），然后计算出一些性质，分析其间可能的关系。接下来就要总结这些关系，直到某种规律出现。研究者们的下一步是用更复杂的例子验证这些关系（从二十面体到更大的随机凸多面体），并去掉无关的性质。如果验证出关系不能成立，或是如果关系成立的理由尚不清楚，那么研究者们就要重新定义寻找个例的标准。然后从头开始循环。

这一流程中，除了一个例外，其他步骤都既需要人类的创造力，又需要计算力。例如，想要分析所选取的个例的性质，就需要利用创造力来识别哪些性质可能相关，然后对这些性质进行计算。唯一没有计算要求的是总结那步，而它可以被认为是创造性流程的核心。这一步要求研究者从具体的个例中提取出一般现象——主要基于直觉。对于多面体来说，这一步骤可能是要将上文中纸笔做的计算扩展到不同维度：同样的模式对二维图形仍然成立吗？对更高维度呢？

虽然AI方法在数学研究中尚未普及，但在之前的几年里已经有多个研究组发表过成果，证明机器学习工具在理论上可以用来从大数据集里面找出相关的个例[2,3]。还有的研究组为了更好地理解这些数据集，使用相关工具估算数学对象的性质，并且准确率很高[4]。Davies和同事则表明，机器学习可以用来辅助研究者进行研究循环中“总结”的步骤，而这一步之前一直被认为主要基于人类的直觉。他们的方法理论上可以应用在数学的许多不同领域。

他们的想法是从一类数学对象的性质出发，先找出两组结构——可能是数字列表或是网络。随后就能假设两组结构间存在某种相关性，其中一个结构可以提供关于另一结构的信息。使用机器学习对大数据集进行这项工作十分理想，因为它可以使用一个结构去猜测另一个结构的细节，其结果点准确性比基于概率要高。

Davies和同事们的方法可以用欧拉定理做一个简单示范。在这个例子里，第一个结构是一组四个数，表示多面体的顶点数、边数、表面积和体积。第二个结构是面数。欧拉公式可以写成这两个结构之间简单的线性关系。在得出和欧拉公式相同结论的过程中，也清楚表明体积和表面积是两个无关的量。使用这一做法来研究欧拉公式很简单，但如果关系式不像这么一目了然的话，情况会复杂得多。这时，机器学习技术就能帮上忙。

作者们成功将他们的技术应用在两个不同的数学领域中，足以证明其成果的进展。他们使用这项技术识别出了纽结理论和组合表示论中此前未知的关系。两个结论对各自领域中的研究者来说并非遥不可及，但它们确实有着领域专家们此前尚未发现的洞见。因此，该成果并不仅仅是抽象的框架。虽然它是否能更为广泛地应用尚不确定，但Davies等人已经给出了一份前途光明的演示，告诉我们能如何使用机器学习工具辅助数学研究中的创造性过程。

参考文献

[1] Davies, A. et al. Nature 600, 70–74 (2021).

[2] Peifer, D., Stillman, M. & Halpern-Leistner, D. Proc. Mach. Learn. Res. 119, 7575–7585 (2020).

[3] Lample, G. & Charton, F. Preprint at https://arxiv.org/abs/1912.01412 (2019).

[4] He, Y.-H. The Calabi–Yau Landscape: From Geometry, to Physics, to Machine Learning (Springer, 2021).

本文经授权转载自微信公众号“Nature Portfolio”。原文以Artificial intelligence aids intuition in mathematical discovery为标题发表在2021年12月1日《自然》的新闻与观点版块上。原文：https://www.nature.com/articles/d41586-021-03512-4?utm_source=Wechat&utm_medium=socials&utm_campaign=d41586-021-03512-4