量子计算机能够以远超传统超级计算机的速度处理一些计算任务。然而，要实现通用的量子计算机，一个巨大的挑战是，如何保护编码信息的量子比特免受噪声干扰？

物理学家发现，一些奇异的量子物相具有长程纠缠模式，可用于量子纠错，保护量子信息，让量子计算更稳健。在 Science 杂志12月2日发表的两篇论文中，研究人员用可编程量子处理器模拟量子物相，并测量其中的长程量子纠缠模式。以下是 Science 介绍这两项工作的评论文章。 

撰文 | Stephen D. Bartlett

译者 | 黄泽豪

审校 | 梁金 

https://www.science.org/doi/10.1126/science.abi8378

https://www.science.org/doi/10.1126/science.abi8794

在非常低的温度下，一些材料可能会凝聚成奇异的物相，其中量子纠缠会成为支配它们行为的主要特征。这些量子物相不同于普通的固体、液体、气体和等离子体，会表现出奇异的性质，例如以不同寻常的方式相互干涉的准粒子激发。从应用角度来看，这些量子物相可能在提高量子存储设备（量子计算机的关键组件）的鲁棒性方面发挥关键作用。 

然而，尽管理论物理学家已经预测这些量子物相在各种条件下的存在，但是在实验上实现具有长程纠缠的量子物相却极为困难。近期，Satzinger 等人[1]和Semeghini等人[2]分别通过使用耦合超导电路和原子阵列，对这些量子物相及其关键特征进行了直接观察。 

1. 奇异的拓扑量子物相

量子物相有很多种类型，其中两个最广为人知的例子是超导体和玻色-爱因斯坦凝聚。由于自旋之间的长程纠缠模式是凝聚态物理学中的基本问题，并且在量子信息系统中具有潜在应用，研究人员一直专注于相关研究。自旋之间的量子关联可以是长程和“拓扑”的，这意味着在连续局部变形下，这种关联不会改变，因此，这种奇异的量子物相被认为具有“拓扑序”。 

在具有拓扑序的量子物相中，研究最多的是那些打破时间反演对称性的相——这意味着如果时间倒流，它们的行为会有所不同。非时间反演对称拓扑相的一个关键实验特征，是它们有鲁棒的边缘模，即沿材料外边缘运行的持续电流。分数量子霍尔效应就是这样一个例子，它引导物理学家发现了拓扑绝缘体和超导体。相反，量子计算机设计者们对时间反演对称的拓扑相更感兴趣，因为这些物相可用于量子纠错，保护量子信息免受噪声、扰动和其他有害影响。 

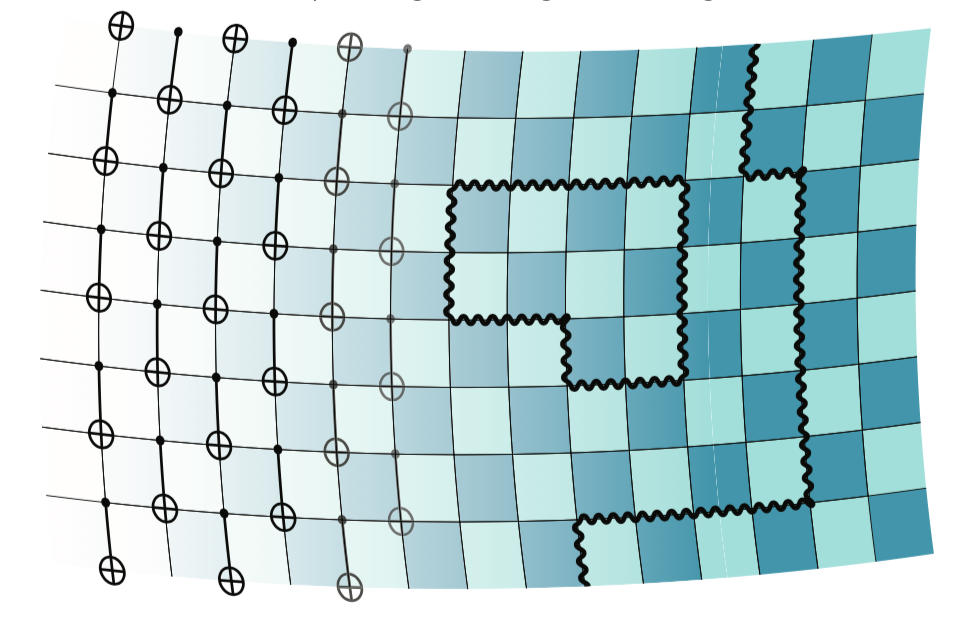
图1. 编织量子拓扑。

图中展示了使用量子处理器构造拓扑相的艺术构想图。左边表示量子电路，可以控制它以形成特定的长程纠缠模式。长程纠缠模式是拓扑量子物相的标志，由右侧的波浪线表示，其中一些形成闭环，一些具有延伸到边缘的开放弦。| 来源：V. ALTOUNIAN/SCIENCE

然而，由于时间对称的拓扑相没有边缘模，其长程纠缠特性不能用传统方法探测，而长程纠缠特性对于其发挥量子纠错的潜力是必要的。由于长程纠缠的基本特性，我们无法通过检查局部区域来了解材料的性质，而必须探测贯穿整个体积的量子关联。观察系统的这种非局域特性需要通过纠缠相互作用和精密测量来对单个量子组分进行精确控制。得益于最先进（但仍处于初级阶段）的量子计算设备，对复杂的多组分量子系统中单个组分的这种控制水平直到最近才成为可能。 

2. 两个实验：量子处理器编程量子物相

Satzinger 等人使用一个由31个耦合超导量子器件二维阵列组成的原型量子处理器。这个量子处理器名为“悬铃木”（Sycamore），2019年因 Google 声称“量子霸权”，即量子处理器能够比传统超级计算机更快地执行某些计算任务，而成为头条新闻[3]。 通过执行一段简短的量子程序，Satzinger 等人使用悬铃木将 toric 编码（toric code）的最低能量态拼接在一起[4]。toric 编码是可用于量子纠错的拓扑有序量子物相的典型例子。这与另一段简短的量子程序一起，使得测量长程量子纠缠成为可能。 他们还开发了其他程序来模拟准粒子的产生，并进行量子干涉实验验证准粒子是否会表现出预期行为。

作者还证明，量子信息可以编码到 toric 编码中以防止出错，并在随后再次读出。这些特性说明，在扩展量子架构时，toric 编码可能成为提升量子纠错能力的关键。 

图2. “悬铃木”（Sycamore）量子处理器。| 来源：Erik Lucero, Research Scientist and Lead Production Quantum Hardware

Semeghini 等人报告了一个不同的实验，目标同样是创建和探索与 toric 编码相关的拓扑有序相的性质。实验中使用光镊将219个原子排列在二维晶格上，组成量子模拟器。通过控制相邻原子间的相互作用，晶格被诱导成拓扑有序相。与悬铃木处理器一样，这个原子量子模拟器也是可编程的。 

研究人员在量子处理器上运行程序，监测处理器的219个原子之间的长程纠缠性质。具体来说，就是测量这些自旋之间如何通过量子关联，沿着一条蜿蜒的路径产生长程纠缠模式，从中我们可以得到直接反映量子物相的拓扑序的数据。Semeghini 等人同样是通过展示编码的信息可以再次读出，演示了如何将量子信息编码到系统中，并为创建量子存储器建立了一条路径。 

图3. 量子自旋液体是一种具有拓扑序的奇异量子物相，具有长程量子纠缠特性，可用于实现稳健的量子计算。Semeghini 等人用可编程的量子模拟器来探测量子自旋液体，第一次实现了对量子自旋液体拓扑序的直接测量。| 来源：Olena Shmahalo for Quanta Magazine

3. 量子计算技术作为工具，探索量子多体系统

这两个实验首次展现了具有时间反演对称性的拓扑有序相的明确证据。它们都不是像往常一样通过新材料实现，而是通过量子处理器虚拟实现。尽管量子处理器提供了一种创建长程纠缠量子态的机制，它们最关键的贡献其实是提供了一种方法来测量表征拓扑序的长程纠缠模式，从而展现了量子计算技术可以成为探索量子多体系统的工具。 

为了在计算过程中保护量子信息，还需要初始化、操纵和测量这些编码中的量子信息，这需要通过使用容错电路来实现。要达到实际应用的目标，量子计算的错误率必须进一步降低到远低于这两个实验所达到的水平。

关键问题是，量子纠错需要对校验算符进行重复测量以发现错误，并通过解码这些测量来更新逻辑信息。这不仅需要一个强大的量子处理器，还需要一个高度集成的经典处理器和控制器[5]。 要实现实用的量子处理设备仍然面临着许多挑战，但这两个实验通过展示利用拓扑量子物相进行纠错，标志着量子计算领域的关键进步。 

参考文献

[1] K. J. Satzinger et al., Science 374, 1237 (2021).

[2] G. Semeghini et al., Science 374, 1242 (2021).

[3] F. Arute et al., Nature 574, 505 (2019).

[4] A. Kitaev, Ann. Phys. 303, 2 (2003).

[5] S. J. Pauka et al., Nat. Electron. 4, 64 (2021).

本文经授权转载自微信公众号“集智俱乐部”。原文链接：Programming a quantum phase of matter. https://www.science.org/doi/10.1126/science.abl8910