在经典力学的图景中，时间是可逆的，发生在过去与未来的事件没有根本区别。但在近50年前，诺贝尔化学奖得主、物理化学家普里高津将不可逆性和时间之箭引入经典热力学，拓展了我们对热力学的理解：不可逆过程不仅可以破坏秩序，增加宇宙的熵，也可以创造高度有序的复杂结构和生命本身。

2017年，在普里高津诞辰100周年之际，美国物理学会（AIP）旗下的非线性科学跨学科期刊 Chaos 发表纪念文章，回顾了普里高津不同时期的学术贡献，以及这位“热力学诗人”与其他科学家的交谊。

撰文 | Dilip Kondepudi，Tomio Petrosky，John A. Pojman

翻译 | 张澳

审校 | 梁金

原文链接：https://aip.scitation.org/doi/full/10.1063/1.5008858

1. 热力学诗人

熟悉伊利亚·普里高津（ Ilya Prigogine）的朋友和同事称他为“热力学诗人”，这是一个恰当的描述。当普里高津谈论热力学和不可逆过程时，人们感觉他理解的内容比他的语言传达的内容更多。我们周围的自然过程是不可逆的，这是事实。不可逆过程不仅增加了宇宙的熵，破坏了秩序，也可以完成与此相反的事情：创造高度有序的复杂结构和生命本身。

普里高津认为这是热力学对自然揭示出的一个深刻方面。当他看到著名的南印度雕塑 Nataraja （跳舞的湿婆，刻画了一支完美平衡创造与毁灭的宇宙之舞）时，他确保在自己的艺术收藏中有一尊艺术价值极高的 Nataraja 青铜雕像。这个雕像的照片成为了他与 Paul Glansdorff 合著的 Thermodynamic Theory of Structure Stability and Fluctuations[1]（《结构稳定性与涨落的热力学理论》）一书的封面。它是热力学的诗篇，是从同一源头涌现出的创造和毁灭，是完美平衡的宇宙之舞。人们可以从普里高津关于热力学的论述中推测出这一切。

图1. Thermodynamic Theory of Structure Stability and Fluctuations（《结构稳定性与涨落的热力学理论》）封面上跳舞的湿婆

耗散结构是近50年前普里高津为不可逆过程所产生的复杂结构而命名的。正如这篇庆祝他诞辰一百周年（普里高津出生于1917年1月25日）的文章所表述的那样 ，耗散结构的研究仍然是一个非常活跃的课题，不断向新领域推进。如果继续研究下去，我们可能会获得更深刻的见解，甚至可能发现新的法则或定理，以更好地理解复杂结构是如何自发形成的，及其对物理参数变化的响应和集体行为。这些在其它领域中的进步，也是我们对生物过程，甚至是那些创造生命的过程的热力学理解的探寻。

普里高津深信不可逆过程在自然界的中心地位和时间之箭的真实性，但他不得不面对令人烦恼的物理学的二元性。从时间可逆的经典力学观点来看，发生在未来或过去的运动（及物质的所有转变）没有根本区别。因此许多人认为不可逆过程和时间之箭不可能是真实的，仅是一个幻觉，是我们因能力有限而创造出来的幻觉。普里高津极其反对关于不可逆过程和时间之箭的这种观点。很多时候，我们看到他在演讲和咖啡馆的谈话中充满激情和确定性地说：“不可逆过程创造了我们，但我们没有创造它们。”有时，他的表述更加文学化：“我们是时间之箭、演化之箭的孩子，而不是其祖先。”

为了适应不可逆过程和时间之箭的现实，必须对经典力学进行修正，或者扩展其表述。为此，他推动了非幺正变换（non-unitary transformation）理论的发展。他在1977年诺贝尔演讲[2]的总结发言中指出：“通过非幺正变换理论引入热力学不可逆性，深刻改变了动力学结构。我们从群到半群，从轨迹到过程。这种演变与本世纪我们对物质世界描述的一些主要变化是一致的。”这个理论至今还在继续发展。

普里高津的科学贡献可以大致分为三个时期：（i）早期，他将热力学重新表述为不可逆过程的科学，改变了热力学在19世纪是关于状态的理论这一状况，（ii）在布鲁塞尔-奥斯汀（Brussels-Austin）小组时期，构建了耗散结构理论，并对不同系统进行了广泛研究，（iii）后期，他的小组专注于扩大经典力学的表述，使不可逆性成为物理学的基础。

2. 关于过程的热力学理论

在工作的第一阶段，普里高津综合了他的导师 Theophile DeDonder 以及 Duhem、Natanson、Jaumann、Onsager等人发展的概念，从根本上改变了热力学的表述，使它成为一个关于过程的理论，而不是一个关于状态的理论。

正如它在19世纪被阐述的那样，热力学确定了两个基本的态函数*（ functions of state ）——能量和熵，前者与热力学第一定律有关，后者与热力学第二定律有关。在这个经典热力学理论中，只有对一个理想的、无限缓慢的可逆过程才能计算熵的变化，即 dS = dQ/T；没有公式能够将熵的变化与自然界中不可逆且以非零速率进行的实际过程联系起来。对于不可逆过程，该理论仅指出 dS > dQ/T，这将不可逆过程排除在外。但该理论仍然非常强大，因为我们可以用可逆过程的概念来计算两个状态之间熵的差异。此外，由于对熵变化的计算局限于无限缓慢的可逆过程，经典热力学无法计算熵的变化率（dS/dt），也无法将熵的变化率与不可逆过程联系起来。

*态函数是描述热力学系统所处状态的宏观物理量（如温度、熵、压强、体积、能量等）的函数。处于平衡态的热力学系统，各宏观物理量具有确定的值，且仅由系统所处的状态决定，与达到平衡态的过程无关。

Bridgman 在他1943年的专著 The Nature of Thermodynamics（《热力学的本质》）中这样描述19世纪经典热力学的状态[3]：“人们几乎总是强调，热力学关注的是可逆过程和平衡状态，它与不可逆过程或远离平衡态的系统无关，在这些系统中，变化是以有限的速度进行。考虑到温度本身就是用平衡态来定义的，平衡态的重要性显而易见。但是，在不可逆过程面前承认热力学的无能为力，似乎是一件令人惊讶的事情。物理学家通常不会采取这种失败主义的态度。”

紧随着 Lars Onsager 在1930年代的进展，普里高津引入了不可逆过程的热力学理论[4-6]。这个理论的关键概念是局部平衡（local equilibrium），它假设每个位置的单位体积内，系统都处于平衡态。因此，温度和其他状态变量成为位置的函数，系统作为一个整体是不均匀的。局部平衡的概念得到了统计物理的支持。统计物理学表明，局部范围内，粒子速度很快就达到了Maxwell 速率分布，从而在每个位置都可以明确定义温度的概念。普里高津的热力学理论定义了系统在时间间隔 dt 内熵的变化 dS遵循

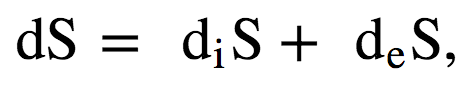
其中 diS 是不可逆过程产生的熵，deS 是由于系统与外部进行能量和物质交换而引起的熵的变化。其中diS与不可逆过程的显式关系通过热力学力 Fk 和热力学流 Jk 建立

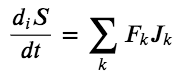
如果用这个表达式来定义每个单位体积内熵的变化率，就可以直接写出整个非均匀体系所有热力学量的正确密度和积分。这就是热力学的现代表述，它让我们对热力学有了更广泛的理解。现在人们可以用化学反应和热传导等不可逆过程的速率来计算熵产生速率。在现代的理论中，热力学第二定律被表述为：diS ≥0。

本文大致介绍了普里高津分别在三个时期的主要贡献。以下内容与第一个时期的贡献有关。普里高津和 De Decker 的文章 “Stochastic approach to irreversible thermodynamics”（不可逆热力学的随机方法）[7]，展示了热力学公式如何扩展至显式包含宏观可观测量的涨落。在这篇综述中，作者们提出了一个数学表述，将涨落、不可逆性以及涨落对熵产生的贡献相联系。

在一篇名为“The underdamped Brownian duet and stochastic linear irreversible thermodynamics” （ 欠阻尼布朗二重态与随机线性不可逆热力学 ）的文章中[8]，Proesmans 和 Van den Broeck 讨论了随机热力学的关键特征，如涨落定理、涨落-耗散关系和涨落时的效率。文章对一个由周期力驱动的布朗粒子的具体例子进行了讨论。

Malek-Mansour 和 Baras 通过一篇名为“Fluctuation theorem：A critical review”（涨落定理: 一篇批评性评论）的文章[9]，对涨落定理进行了批判性的评论。该定理有许多微妙的特征，不幸导致了一些声称可以违反热力学第二定律文章的产生。引用普朗克（Max Planck）的话，作者正确地提醒读者，热力学第二定律是一个宏观定律，表明了第二类永动机的不可能性，它要么在所有系统中有效，要么在所有系统中无效，没有第三种可能性。这篇文章指出了在应用涨落定理时需要仔细考虑的几个方面。

3. 广泛存在的耗散结构

在普里高津的领导下，活跃的热力学和统计力学的布鲁塞尔学派蓬勃发展，出版了高度成功的专著[10-12]，并被翻译为多种语言。如今，在纳米和其他技术的刺激下，热力学正在产生新的发展。
 

在20世纪50年代末和60年代初，随着人们认识到非平衡条件可能产生化学振荡，一个新的活跃阶段开始了。它起源于这样一种认识，不可逆过程可以在系统远离热力学平衡时，驱动系统进入有组织的状态；自组织（self-organization）现象开始被人们认识。不可逆过程产生被认为代表无序的熵，然而，同样的不可逆过程也产生了自组织，耗散结构的研究由此产生。这是理解秩序的起源以及我们在自然界中看到多样形式和功能的关键。这也引起了有关非平衡态稳定性的新问题，对描述远离热力学平衡的系统方程存在非线性的发现，以及许多自组织系统的发现。

1967年，当普里高津接受了德州大学奥斯汀分校（University of Texas in Austin）统计力学和热力学研究中心的主任职位时，他的团队扩大成了布鲁塞尔-奥斯汀团队。耗散结构的研究进入了一个新阶段，吸引了世界各国的研究人员。因此，诺贝尔化学奖于1977年授予普里高津，以表彰他对热力学的贡献。他与 Grégoire Nicolis 合著的书总结了当时有关耗散结构的许多工作，也在同年出版[13]。几年后，普里高津在新书《从混沌到有序》（Order out of Chaos）中[14]，对时间、复杂性以及不可逆过程有了更广泛的描述 。这本书被翻译成18种语言，广为流传。随后，普里高津为普通读者写了几本关于时间之箭和复杂性的书。耗散结构研究仍然是一个蓬勃发展的研究领域。

关于耗散结构的文章是本文介绍的主要部分。Albert Goldbete 对生物化学振荡领域的贡献是众所周知的，他在 “Dissipative structures and biological rhythms”（耗散结构与生物节律）一文中[15]，提出了一个令人兴奋的绝妙评论。该文中的一张表格（见表1）展现了周期性在细胞和超细胞水平的惊人存在。

表1. 发生在生物组织各个层面的主要生物节律，自上而下节律周期递增，其周期长短的差异超过10个数量级 | 来源：Goldbeter, Albert. “Dissipative structures and biological rhythms.” Chaos (Woodbury, N.Y.) vol. 27,10 (2017): 104612. doi:10.1063/1.4990783

在同一领域，Amemiya 等人一篇名为“Primordial oscillations in life：Direct observation of glycolytic oscillations in individual HeLa cervical cancer cells”（ 生命中的原始振荡：对海拉宫颈癌细胞中糖酵解振荡的直接观察）的文章[16]，发现并概述了糖酵解振荡在细胞节律和癌细胞中的作用。作者还讨论了自组装及其与耗散结构的关系：耗散结构和自组装互相辅助。

Kondepudi、Kay 和 Dixon 等人在 “Dissipative structures, machines and organisms：A perspective”（耗散结构、机器和有机体：一种观点）一文中[17]，讨论了耗散结构在理解生物体中的相关性。作者提出了一个电压驱动的系统，能够惊人地展现类似于我们在有机体中看到的行为。他们表明，在该系统中观察到的几乎所有复杂行为的不同方面，都可以被描述为一种向更高的熵产生速率状态的演化。也可以在这篇文章中找到关于机器和有机体之间根本区别的观点。

耗散结构最著名的一个方面是解释斑图如何在远离平衡的化学系统中形成。Burdoni 和 De Wit 在他们题为“Dissipative structures：from reaction-diffusion to chemo-hydrodynamic patterns”（耗散结构：从反应-扩散到化学流体动力学斑图）的文章中[18]，讨论了反应和扩散之间的相互作用如何在不同的反应物相互接触时产生局部的时空斑图。他们使用布鲁塞尔振子模型（Brusselator model，见图2），发现了局部波、图灵斑图和反应-扩散斑图。

图2. 布鲁塞尔振子模型最初由普里高津和他的同事们提出，是模拟自催化反应的一组非线性微分方程。图中是二维空间中反应-扩散系统的布鲁塞尔振子模拟。| 来源：维基百科

在文章“Chlorine dioxide-induced and Congo red-inhibited Marangoni effect on the chlorite- trithionate reaction front”（亚氯酸盐-连三硫酸盐反应界面的二氧化氯诱导和刚果红抑制马伦哥尼效应*）中[19]，Liu 等人研究了马伦哥尼对流对亚氯酸盐-三硫酸盐反应界面的影响。反应过程中产生的二氧化氯改变了表面张力，导致液体流动。然而，刚果红的加入产生了一个振荡界面，溴酚蓝产生了多个涡旋。

*马伦哥尼效应是指在存在表面张力梯度地流体界面上，表面张力强的液体比表面张力弱的液体对周围液体的拉力更大，导致表面张力弱的液体向强的方面渗透。意大利物理学家马伦哥尼（Carlo Marangoni）在1865年的论文中首次研究了这一现象。

Biria 等人回顾了光反应系统中的光波，他们的文章“Coupling nonlinear optical waves to photoreactive and phase-separating soft matter：Current status and perspectives”（耦合非线性光波到光反应和相分离软物质：现状和前景）[20]，讨论了非线性光学动力学如何与相分离耦合，以创造具有实际用途的斑图形成。

Viner 等人在文章“Effect of pseudo-gravitational acceleration on the dissolution rate of miscible drops”（赝重力加速对混相液滴溶解速率的影响）[21]，研究了旋转液滴张力计中的旋转加速度对混相液滴溶解的影响，张力计中的高旋转速率创造了一个赝重力场，进而产生了一个阻碍溶解的作用力（气压扩散），但也创造了一个浮力驱动的流以促进溶解。

Bunton 等人的文章“The effect of a crosslinking chemical reaction on pattern formation in viscous fingering of miscible fluids in a Hele–Shaw cell*”（交联化学反应对 Hele-Shaw 盒中混相流体粘性指进斑图形成的影响）[22]，研究了硫醇与丙烯酸酯的交联反应对 Hele-Shaw 盒混相流体粘性指进斑图形成的调节作用，他们发现可以通过调整反应速率来改变斑图。

图3. Hele-Shaw 盒由中间存在一个微小间隙的一对平行板组成，以1898年研究该问题的 Henry Selby Hele-Shaw 的名字命名。其重要性体现在Hele-Shaw 流可很好地近似流体力学中的各种问题。| 来源：维基百科

普里高津在60岁获得诺贝尔化学奖的时候，已经开始思考如何修改力学，以纳入不可逆性和时间之箭，从而开始了他研究的第三阶段。但是这个问题困扰着他之前的许多人，包括像庞加莱（Henri Poincaré）这样的人，而且它涉及到动力系统的核心。

庞加莱将动力系统划分为可积和不可积系统，这是普里高津思想的重要来源。庞加莱证明在不可积系统中，不可能通过作用于相应的未扰动不变量，来构造一个正则或幺正变换，产生新的运动不变量。普里高津看到了这个结果和不可逆性之间的联系。此外，“混沌系统”表明动力学不是一门能让我们无限预测未来行为的科学，普里高津从中看到了经典力学的局限性，也发觉必须以概率和不可逆性作为拓展经典力学的根基。为此，他和他的合作者开始构建一个非幺正变换理论，在这个理论中，概率的出现不是因为我们无法确定微观状态，而是不可积系统中共振奇点（resonance singularities）的动力学结果。直到2003年去世前都，他都在研究这一理论。如今该理论也在继续发展。

4. 超越动力学

普里高津科学贡献的第三个阶段分析了有无穷多自由度的开放动力系统的哈密顿系统的不可逆过程，并分析了混沌系统和量子光学中的非线性过程。
 

Petrosky 等人的“Microscopic description of irreversibility in quantum Lorentz gas by complex spectral analysis of the Liouvillian outside the Hilbert space”（希尔伯特空间外刘维尔函数的复合光谱分析对量子洛伦兹气体不可逆性的微观描述）[23]，讨论了刘维尔函数的复合光谱分析的应用。普里高津和他的布鲁塞尔-奥斯汀小组发展了该类分析。对于量子洛伦兹气体，他们证明了哈密顿系统的不可逆过程是在所有空间和时间尺度上纯粹的动力学基础上获得的，包括微观原子相互作用范围在内，而不依赖于任何唯象操作。

Ordonez 和 Hatano 的文章 “Irreversibility and the breaking of resonance-antiresonance symmetry”（共振-反共振的不可逆性和对称性破缺）[24]，使用一个单位点耦合到格点中两个引线的简单模型作为例子，提出了一个有趣的时间反转对称的单位分解，来描述开放量子系统的不可逆过程。结果表明，这种单位分解既包含将在未来衰减的共振态，也包含将在过去衰减的反共振态；一个时间反转不变状态同时包含等权重的共振分量和反共振分量，然而随着系统的演化，这种对称性将自动破坏。

Fathi 等人的文章“A wave-function model for the CP-violation in mesons” （介子 CP 不守恒的波函数模型）[25]，利用二能级 Friedrichs 哈密顿模型讨论介子中的 CP 对称破缺。Friedrichs 模型一直是普里高津和他的同事分析的原型模型之一。该模型描述了不可逆性的动力学根源，这里的不可逆性来自与时间方向对称的基本运动方程解中出现的共振奇异性。

Hasegawa 等人的“Generalized second law for a simple chaotic system”（简单混沌系统的广义热力学第二定律）一文[26]，讨论了热力学第二定律（非平衡最大功表述，nonequilibrium maximum work formulation）在一个简单混沌系统中的推广。他们表明，即使对于一个吉布斯-香农熵守恒的系统，热力学熵也会增加。

Barr 等人的文章“Signatures of chaos in the Brillouin zone”（布里渊区混沌的信号）[27]还讨论了铺设在无限平面上的量子台球的混沌行为。他们表明，当台球的经典动力学行为从有序变为混沌时，布里渊区的能带开始混合。

最后，Vanbever 等人的文章“Semiconductor surface emitting lasers for photon pairs generation”（半导体表面发射激光器用于产生光子对）[28]讨论了量子光学中的非线性过程。这种非线性过程一直是普里高津最喜欢研究的课题之一。他们研究了通过三阶非线性及四波混频相互作用在共振垂直腔表面发射激光器（Vertical-Cavity Surface-Emitting Laser，VCSEL）中产生光子对的可行性。

我们纪念普里高津不仅仅因为他是一个充满活力并鼓舞人心的同事，也因为他是一个非常善良且慷慨的人。他喜欢与人交往，经常与同事共进晚餐。他一生都一直欢迎来访者，并给予他们慷慨的支持。他是一个热心的艺术收藏家，收藏有博物馆级别的前哥伦布时期的艺术品。他在年轻的时候，也是一个有成就的键盘音乐家。他的墓志铭上写道：

L'ÉTONNEMENT EST SOURCE DE CRÉATIVITÉ

（惊奇是创造力的源泉 ）

纪念回顾

普里高津是Dilip Kondepudi的博士导师。Kondepudi 在获得博士学位后继续与普里高津合作了多年，他们一起发表了许多文章。1998年，他们合著了一本题为 Modern Thermodynamics：From Heat Engines to Dissipative Structures（《现代热力学：从热机到耗散结构》）的教科书，该教科书以六种语言在25个国家出版使用。Kondepudi 与我们分享了一段与 普里高津 有关的珍贵回忆：

我在University of Texas in Austin 的时候，有好几次普里高津来到我的办公室，习惯性地用左手轻拍他的胸部说道：“ Dilip，让我们去喝点咖啡吧……如果可以的话。”我认为这意味着他想离开办公室，理清头脑中的一些想法。我喜欢与他进行的那些非正式讨论。我有机会目睹他通过讨论形成一个想法的过程，了解他对我正在思考的一个想法的意见，并请他解释一些他在最近的演讲中说过的我不理解的东西。我们经常去大学附近的一家小面包店，店名很长，叫“ aptain Quackenbush's Intergalactic Dessert Company and Espresso Café（船长的星际甜点公司和咖啡店）”。我们坐在那里，喝着一杯上好的欧洲咖啡，他经常谈及物理学需要有所改变，将不可逆性纳入基础原理中。我仍然能在脑海中听到他的声音：“太神奇了，人们竟然坚信时间是可逆的。”我特意带上本子和笔，去咖啡室聊天。有一天，他写了一篇结合广义相对论和热力学而使不可逆性成为基本原理的论文。我在里面看到了一个宏伟的计划，于是留下了那张纸，现在它被保存在普里高津的纪念册里。

Tomio Petrosky 在1980年遇到了普里高津，并与他密切合作。在普里高津生命的最后阶段，Tomio Petrosky 是他最亲密的同事之一。他们一起撰写了许多论文，还经常去 Kondepudi 在上文提到的面包店，在那和 普里高津 谈论各种话题。他回忆道：

我们偶尔会听到普里高津的至理名言。他说：“我生命中有两件最重要的事情。一个是与人相遇。另一个是和我的同事讨论。如果你不讨论，你只能得到你预料中的结果。”一次在日本的新闻发布会上，普里高津被问及他科学工作的动力和动机是什么。他回答说：“是不满！在我看来，许多科学家对目前物理学基本定律的解释感到满意，尤其是那些有关时间的解释。我觉得有些事不能令人满意。消除这种不满是我继续科学研究的强大动力。”

John Pojman 在1984年至1988年间是德州大学奥斯汀分校的一名研究生。他回忆起普里高津是如何影响他的职业生涯的：

我在乔治城大学（Georgetown University）的大四学年时，开始对化学自组织感兴趣。我拜访了 Joseph Earley 教授，他三年前在我的普通化学课上演示了 Belousov-Zhabotinsky 反应*，他说我应该去德州大学奥斯汀分校的研究生院，和 普里高津 教授一起工作。1984年春天，我申请了德州大学并访问了奥斯汀分校。我给普里高津教授写了一封信，与他进行了一次会面。他穿着拖鞋在公寓楼的大厅等我，并邀请我去他的公寓。他非常亲切地说：“我有半个小时的时间，你想谈些什么?”我不记得我回答了什么，但他接着就时间之箭以及帝国如何衰落、崛起发表了演说。我被他的思路迷住了，并最终进入了德州大学，在那里我与普里高津教授和 James Whitesell 教授共同研究化学。在普里高津访问德州大的期间，我每年会见他两次，他会持续激发我对自组织的兴趣。虽然我的导师实际上是 Dilip Kondepudi，他当时是一个博士后，但普里高津教授一直在支持我研究聚合物交换反应的 Maxwell-Boltzmann 气体。

Belousov-Zhabotinsky 反应的计算机模拟。Belousov-Zhabotinsky 反应，又被称为BZ反应，由苏联化学家和生物物理学家 Belousov 于1951年首次发现，开创了现代非线性化学动力学的领域。该反应是一类远离平衡态的化学振荡反应，其产生机制与图灵斑图类似，可以通过反应-扩散方程定性解释。

参考文献

[1]P. Glansdorff and I. Prigogine, Thermodynamic Theory of Structure, Stability and Fluctuations ( John Wiley Sons, New York, 1971), Translations in French, Russian and Japanese.[2] “Ilya Prigogine - Nobel Lecture: Time, Structure and Fluctuations,” Nobelprize.org. Nobel Media AB 2014.[3]P. W. Bridgman, The Nature of Thermodynamics ( Harvard University Press, Cambridge, MA, 1943), p. 133.[4]I. Prigogine, Etude thermodynamique des ph énomènes irr éversibles ( Dunod, Paris et Desoer, Li`ege, 1947).[5]I. Prigogine, Introduction to Thermodynamics of Irreversible Processes ( Charles C. Thomas Publisher, Springfield, Illinois, 1955).[6]I. Prigogine, Introduction to Thermodynamics of Irreversible Processes, 3rd ed. ( John Wiley & Sons, New York, 1967).[7]G. Nicolis and Y. De Decker, Chaos 27, 104615 (2017).[8]K. Proesmans and C. Van den Broeck, Chaos 27, 104601 (2017).[9]M. Malek Mansour and F. Baras, Chaos 27, 104609 (2017).[10]I. Prigogine, V. Mathot, and A. Bellemans, The Molecular Theory of Solutions ( North Holland, Amsterdam, 1957).[11]I. Prigogine and R. Defay, Chemical Thermodynamics ( Jarrold & Sons, Norwich, 1958).[12]I. Prigogine, Nonequilibrium Statistical Mechanics ( John Wiley & Sons, New York, 1962).[13]G. Nicolis and I. Prigogine, Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations ( John Wiley, New York, 1977).[14]I. Prigogine and I. Stengers, Order out of Chaos ( Bantam, New York, 1984) [French version: La Nouvelle Alliance - Les Métamorphoses de la Science (Gallimard, Paris)].[15]A. Goldbeter, Chaos 27, 104612 (2017).[16]T. Amemiya, K. Shibata, Y. Itoh, K. Itoh, M. Watanabe, and T. Yamaguchi, Chaos 27(10), 104602 (2017)[17]D. Kondepudi, B. Kay, and J. Dixon, Chaos 27(10), 104607 (2017).[18]M. A. Budroni and A. D. Wit, Chaos 27(10), 104617 (2017).[19]Y. Liu, X. Ren, C. Pan, T. Zheng, L. Yuan, J. Zheng, and Q. Gao, Chaos 27(10), 104610 (2017).[20]S. Biria, D. R. Morim, F. A. Tsao, K. Saravanamuttu, and I. D. Hosein, Chaos 27(10), 104611 (2017).[21]G. Viner, T. La Monica, R. Lombardo, and J. A. Pojman, Chaos 27, 104603 (2017).[22]P. H. Bunton, M. P. Tullier, E. Meiburg, and J. A. Pojman, Chaos 27, 104614 (2017).[23]T. Petrosky, K. Hashimoto, K. Kanki, and S. Tanaka, Chaos 27, 104616 (2017).[24]G. Ordonez and N. Hatano, Chaos 27, 104608 (2017).[25]S. M. S. Fathi, M. Courbage, and T. Durt, Chaos 27, 104605 (2017).[26]H. H. Hasegawa, T. Nakamura, and D. J. Driebe, Chaos 27, 104606 (2017).[27]A. Barr, A. Barr, M. D. Porter, and L. E. Reichl, Chaos 27, 104604 (2017).[28]L. R. Vanbever, E. Karpov, and K. Panajotov, Chaos 27, 104613 (2017).

本文经授权转载自微信公众号“集智俱乐部”。