撰文 | Anna Ned

翻译 | zhenni

审校 | Dannis

来源：https://commons.wikimedia.org/wiki/File:Dan_Shechtman_in_1985.jpg

科学界的八卦一般不会特别流通，但通常你在科学界待的时间越久，就越会容易听到一些令人惊讶的智力论战，收获职业生涯里一两个亦敌亦友的伙伴。

其中一段有趣的科学争论在一位敢于拿职业生涯来打赌的自信工程师和一位二十世纪最伟大的科学家之一——鲍林（Linus Pauling）之间展开。在鲍林于十年后去世的时候——显然到这一刻他也没有完全接受这个理论——鲍林的对手收获到了所有陷入过科学论战中的人都会梦寐以求的结果。学界在几年内慢慢接受了他的说法，这位工程师也凭借他突破性的想法获得了诺贝尔奖。

晶体学理论

这个故事要从一个理论讲起。在进入正题前，我们需要介绍一下人们以往一直用于研究的经验和工具，由此我们才能理解这个突破有多么“叛逆”，以至于动摇了人们所熟知的晶体学基础。
如何将一个或多个几何形状铺满表面——或者我们称之为“镶嵌”问题，是数学领域一个古老而有趣的课题。很长一段时间以来，人们都认为欧几里得平面不能被一些几何面（比如正五边形）平铺。科学学科中，晶体学限制理论（crystallographic restriction theorem）指出，只有某些周期性方法才能平铺空间。用材料科学的方式来表述的话，晶体中的原子只能按某几种周期性进行排列，现代晶体学理论就是以数学中的离散群论作为基础的。

来源：https://en.wikipedia.org/wiki/Wallpaper_group#/media/File:SymBlend_p4.svg
 

晶体学限制定理（原始版本）：

一个晶体的旋转对称性（二维或三维空间中）只存在2重、3重、4重和6重旋转对称性。

这个定理数学上有更严格的证明，但这里我挑选了一个更简单、方便理解的：

将相邻的原子连接成一个正多边形，其内角和为180°×(n-2)，除以边数n必须为360°的除数：

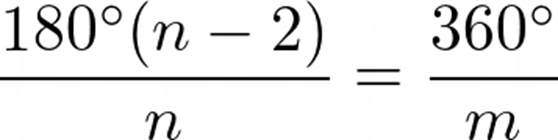
那么：

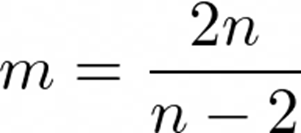
m需要为整数，为了满足等式，则n = 2, 3, 4, 6. 这意味着无限大晶体的对称性必须满足2、3、4、6重对称性。
 

推 论

从晶体学限制定理可以得出在二维空间中有五种周期性的排列方式，我们称之为五种晶格，如下图中所示。这些可以由一组平移操作得到的无限点阵的最小重复单元被称为布拉菲格子（Bravais lattice）；类似的，三维空间存在14种可能的布拉菲格子，隶属于七种晶系（三斜、单斜、正交、四方、立方、三方以及六方晶系）。

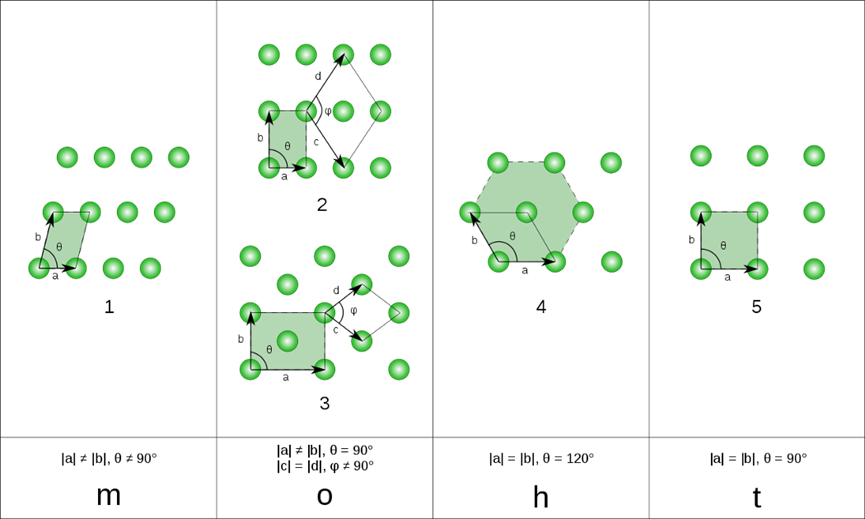
二维空间中五种可能的布拉菲格子，属于四种晶系——单斜（2重旋转对称性）、正交（2重旋转对称性）、六方（6重旋转对称性）和四方（4重旋转对称性）晶系。来源：https://upload.wikimedia.org/wikipedia/commons/e/ee/2d-bravais.svg

虽然点群的数量是无限的（保持固定原点的保距同构），但有了晶体学限制定理约束，只有有限数量的点群对称性操作（对映、旋转、或旋转对映）能存在于上述晶格中。周期性宏观晶体的对称性可以由以下因素产生：

· 晶格对称性

· 点群对称操作（可以伴随平移操作——也就是有螺旋轴或者滑移面）

这意味着所有周期性晶体属于一个有限集合当中的某一种。对于二维平面，所有周期性晶体都有可以按17种二维空间群（墙纸群）归类；而所有三维的周期性结构则归类进230个空间群当中。

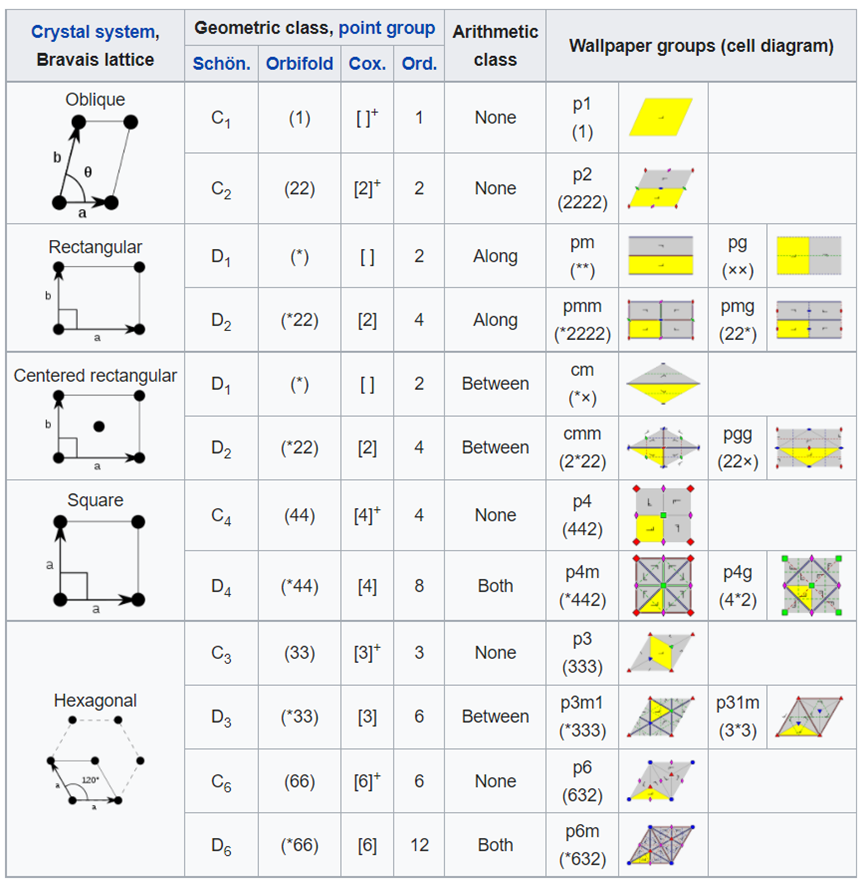
17种可能的墙纸群（wallpaper group）由所有可能的点群对称性操作（可以伴随平移操作）获得。来源：https://en.wikipedia.org/wiki/Space_group

复杂的现实

但自然界中发现的大多数晶体都是以多晶形式（polycrystalline）存在的，它们由许多单一晶相组成的小区域组成。多晶材料的对称性通常难以表现出来。

长在木头上的石岩（岩盐矿）以多晶的形式结晶，表现出立方对称性。岩盐矿（氯化钠）结构属于立方晶系，空间群为Fm-3m。来源：https://commons.wikimedia.org/wiki/File:Halite_on_wood_MNHN_Min%C3%A9ralogie.jpg纯的单晶具有三维230种空间群中的一种，通常是在实验室以特定条件生长的（需要特定的温度、压强、组分浓度等等参数）。几十年来，专攻晶体生长和晶体学的科学家在晶体制备及探索，还有晶体性质研究等许多方面发展出了大量高精尖技术。

教科书定理之例外

我回顾的这些基本内容在过去的数十年已为人所熟知，这些内容对理解当时晶体学家的观点和经验很重要。尽管已经发展出了一系列的相关技术以及用数学语言写就的晶体学理论，许多有关晶体生长鉴定的挑战和挫折仍然广为人知。熟悉了当时的背景后，当听到有人声称发现了一种具有不可能的五重对称性的晶体时，你会作何反应呢？

这件事就发生在1984年。在NIST（美国国家标准与技术研究院）研究与收集了两年的数据后，谢赫特曼（Dan Shechtman）和同事发表了自己的结论，声称发现了一种具有二十面体对称性的晶体，这种晶体具有六个禁止的五重对称轴。[1]他们观察到的这种缺乏平移对称性的晶体并不能按现有的对称性体系进行分类，尽管这种基于14种三维布拉菲格子的体系在过去的几十年间已经被广为认可。同年，另一个团队发表了一篇理论分析来支持这一意外的发现。他们提出了一种只有一个旋转中心的非周期性平铺方式，并给这种此前未发现的结构起了名字——准晶体（quasicrystal）。[2]准晶体不具有局域的周期性，但是仍能表现出长程有序。

这个发现吸引了一大批关注，但是负面的。第一个反对的声音：准晶体之前未在晶体学研究中发现，说明自然界中这样的结构不能稳定存在。此前科学家们一直都在研究原子可能的排列，但好像是更专注于几何学的活动，而非对现实材料的研究。很多人认为一些时候能观察到的所谓禁止的十重对称性衍射图案是孪晶产生的结果，而非真正的被禁止的对称性。孪晶是两个分离的晶体共用一个界面相对生长的产物，在晶体学中是一个普通的问题，会造成复杂的衍射图样。

属于四方晶系的金红石孪晶（二氧化钛），其空间群为P42/mnm。来源：https://commons.wikimedia.org/wiki/File:Rutile-41432.jpg

和大人物之间的冲突

莱纳斯·鲍林（左）和达尼埃尔·谢赫特曼（右）来源：https://commons.wikimedia.org/wiki/File:Dan_Shechtman_in_1985.jpg当谢赫特曼首次在所在NIST的研究团队公布了自己的数据和结论时，他团队的领导，同时也是一位在以色列理工学院担任教授的40岁的科学家说：“你还是回去好好看看课本吧。”几天后，这位领导以“给团队带来污点”为由，让谢赫特曼离开了NIST。从已有的资料我们很难看出，谢赫特曼究竟是在发表数据时被开除的还是被迫休假的。两次诺贝尔奖得主（一次化学奖一次和平奖）、在化学和医药领域有超过350篇出版物的作者、量子化学创始人之一、被誉为“分子生物学之父”、“化学圣经”的作者 [3]鲍林（Linus Pauling），也是众多不相信这一发现的人之一。鲍林立马私下写了一封信件，试图说服作者重新分析这些数据，甚至还申请了一份数据的副本用来自己分析。[4]谢赫特曼立刻回应并发送了数据，还提供了许多支持最初发现的附加数据。即使是这样一个友好语气下的辩论，他们俩也没说服对方。鲍林告诉谢赫特曼自己会写一篇对于这个数据的不同解释。于是在初始发现的一年后，鲍林的不同解释以论文形式发表在《自然》上——这是一个期刊排名远高于原始工作发表的期刊。这篇文章也将是关于从谢赫特曼和同事那里获得的数据的另外解释的系列文章的第一篇。鲍林以这句话给文章结尾 [5]：
“晶体学家们现在可以不用担心别人质疑自己学科基础的有效性了。”一年后，鲍林在与谢赫特曼的深入的私人交流中说，他在自己的数据分析中发现了一个错误。鲍林写道 [4]：
“这个错误让我几个月的努力打了水漂。”谢赫特曼说服鲍林这里并没有错误。意识到自己的问题后，鲍林开始解决这个数据分析的其它“漏洞”，决心解决这个“准晶体问题”。根据已有的信件，两人的对话在鲍林一方的亲切和粗鲁之间反复横跳。由于谢赫特曼并不放弃在会议上大方展示自己的发现，鲍林在几百个科学家面前喊出了下面这段话——他本人也因此而闻名 [6]：
“根本就没有准晶体这种东西！有的只是‘准科学家’。”在1987年后，也就是有关于准晶体最开始的论文发表的三年后，二人的对话就没有记载了。两人仍然向对方表达了谢意，鲍林这样写道：
“你的发现也令我很开心……两年来我一直致力于这个问题，并在过程中享受许多。我估计已经在上面花费了近1000个小时来思考整个问题，并花费了1000多小时计算和写论文。”然而，鲍林好像一直处于坚持解决“准晶体问题”的工作中，许多其他的科学家也在支持和鼓励他进行这项工作，其中就包括保罗·斯坦哈特（Paul Steinhardt），一开始进行理论计算支持准晶体存在的共同作者之一。在1989的论文中，鲍林抱怨自最初发现的五年来这个课题已经发表了1500余篇理论和实验的论文。他写道 [7]：
“已提出的简单的准晶体理论需要被修改。”在最初发现的六年后，鲍林建立了一个包含超过1000个原子的多重孪晶元胞模型来解释数据 [8]——虽然他又错了，但值得赞赏的是，在这篇反对的论文于1984年发表时，他已经83岁了。我在1990年后就未在找到他所作的关于准晶问题的文章了，尽管这个问题仍出现在他90岁，也就是1991年的私人笔记里 [9]。1992年，国际晶体学联盟改写了对晶体的定义。1994年，鲍林去世，享年93岁。

从冒着丢掉工作的风险反叛到获得诺奖

80岁的谢赫特曼教授如今已经是广受敬重的科学家了，他在以色列理工学院和爱荷华州立大学任职材料科学教授。尽管他最初的发现颇具争议，但仅在成果发表三年后，另一个团队就报告发现了另一种更纯、更稳定的准晶体材料 [10]。从数学的观点来看，我们也可以理解最初以平移对称假设为基础的理论。非周期性的平铺早在1960年代就被艺术界和数学界所熟知了，最具名气的非周期性平铺的例子莫过于二维的彭罗斯平铺（Penrose tiling）。其三维结构可以类比为二十面体平铺（icosahedral tiling），和谢赫特曼教授和同事当初观察的晶系一致。

一些可能的彭罗斯平铺。来源：https://en.wikipedia.org/wiki/Aperiodic_tiling#/media/File:Penrose_LI_classes.svg获得非周期性平铺的方式有许多，但不像只允许平移对称性存在的对称性分类的点群晶系，可能的非周期性平铺的数目是无穷多的。

所有三维的周期性晶体都可以被归类至230种空间群当中。而准晶可能的数目是无穷的。来源：https://unsplash.com/photos/g95sf8-fEQg

如今谢赫特曼教授已经无惧于分享与鲍林冲突的观点了，他这样说道 [11]：“有很长一段时间我都在反对全世界，我成了一个荒诞的代名词，是晶体学基础课程会提到的教材。而与我的发现相对抗的，是以两度获得诺奖、美国化学学会的偶像以及世界上最著名的科学家之一的莱纳斯·鲍林为首的人们。多年来，直到鲍林临终前，都在和晶体的准周期性作斗争。他错了，而我在之后的一段时间里都在享受这个知道他错了的美妙的科学争论的过程。”谢赫特曼的先锋工作被认可了，他因发现准晶体而独享了2011年的诺贝尔化学奖。而当我们重看晶体学限制定理，只能严谨地将其改成编辑后的版本：

晶体学限制定理（改编版）：如果平面中一组离散位移具有多个旋转中心，那么可能的旋转只有2、3、4、6重旋转。

本文经授权转载自微信公众号“中科院物理所”，原标题为《成为准诺奖得主的条件竟是让另一位诺奖得主讨厌……？》。

原文链接：NobelPrize to Guy Who Another Laureate Said is Not a Real Scientist | by Anna Ned |Cantor’s Paradise (cantorsparadise.com)