如果有人对你说，把一个苹果切成有限份，通过平移和旋转将其重新组合起来，可以得到两个和原来体积完全相同的苹果，这样反直觉的结果你会相信吗？尽管这种操作在现实中不可能，但在数学上是可以能的——这就是Banach–Tarski定理。本文将详细介绍这一定理的证明，特别是其依赖的选择公理，并详细谈谈如何理解这一定理背后所折射出的不同数学思想。

撰文 | 叶凌远

‍‍‍引言

当你饥肠辘辘身处绝境，手中只有一个苹果，你会怎么办？如果这时数学家告诉你，她可以把这个苹果切开分成有限份，再重新组合起来，你就能得到两个和原来苹果一样大小的新苹果——你是否为了活命，愿意重拾久违的数学，开始虔诚地学习？

这听起来匪夷所思，违背常理。的确，在现实生活中，我们没有办法真的把一个苹果切开再重组，得到两个和原来一模一样的苹果。但在数学上，真的有一个定理说的就是这样一种现象，这就是著名的 Banach-Tarski 悖论（中文中有时也称作分球悖论）：对于三维空间中的一个球（更一般地对于任意 维空间中的球），我们可以找到一种方式把这个球切分成有限份（例如5份即可），将得到的每一小份通过旋转和平移重新组合起来，就能够拼凑出两个和原来大小一模一样的两个球。

严格来说这并不是一个“悖论”，而是一个定理，因此之后我们都将会称其为 Banach-Tarski 定理，该定理最早的证明是Stefan Banach和Alfred Tarski在一篇1924年的文章中给出的。之所以将其称为“悖论”，是因为这个定理的结论与我们的常识和对几何的直观有些冲突，正如前文说数学家能凭空变出来一个新苹果时，你所感到的怀疑一样。

此时，如何认识这样一个“悖论”就变成了更为重要的事情。我们应该无条件地相信这个定理所阐述的内容，重新构建我们对几何物体的直觉吗？还是我们应该更相信直觉，从而反过来重新审视我们描述这个定理时所做的一些更基本的假设？现在，我们就来仔细探讨这个问题。

Banach-Tarski 定理的证明

为了更加深入地探讨这个定理，我们还需简单地了解一下这个定理所涉及的一些概念和思想，同时也会讲讲这个定理的证明。对于人类而言，数学证明的要素并不仅仅在于保证一个命题的正确性，更在于让我们从证明当中体会什么是对一个命题而言最核心的要素，掌握了这些，我们才能进行后面更加深入的探讨。

无穷

若暂时跳出我们对三维球体的几何直观，从更为抽象的角度来考虑，似乎这件事情没有预想的那样违背直觉，因为这涉及到无穷对象。在数学上，可以说是在 Cantor 创立现代集合论之后，我们才真正有足够的数学工具来对无穷本身进行研究，同时也发现了无穷非常有趣的性质。

在观念上，对无穷最重要的认识是，比较两个无穷的大小是通过寻找两者之间的一一对应来完成的。例如，所有偶数 0, 2, 4, ... 和所有自然数 0, 1, 2, 3, ... 的“个数”，或这两个无穷的大小，是一样的，因为我们只需把每个自然数都乘以2，就找到了其与所有偶数之间的一个一一对应。同样地，如果我们把三维空间中的球记为 ，其是如下的一个集合，

作为集合， 和 （即两个球所构成的集合）是同构的，即在数学上我们能够找到这两个集合之间的一个一一对应。所以，至少从抽象集合的角度，其并没有排除 Banach-Tarski 定理存在的可能性。

几何

但 Banach-Tarski 定理所说的并不仅仅是能够找到 和 之间的一个同构——这件事情很容易做到。更为重要的是，定理中叙述的对 进行切分再重组的过程需要保持其几何性质，即我们只能通过平移和旋转来移动切分后的部分，而不能进行任何拉伸或撕扯。例如，前文所述所有自然数和所有偶数之间的同构从某种意义上便改变了其几何性质，因为我们将自然数轴进行了拉伸。这样找到的同构是不满足Banach-Tarski定理的要求的。

现代数学的发展也时刻挑战着我们从古典几何中获得的直觉，Banach-Tarski 定理并不是特例。一个同样具有“悖论”性质的结论是，可以用一根直线填满一个平面。这就是著名的 Peano 曲线，也被称为空间填充曲线（space-filling curves）。Giuseppe Peano 是第一位找到这种曲线的数学家，因此也以他的名字统称所有满足这样性质的曲线。

Peano 曲线的存在似乎也不符合我们的几何直观：怎么能用直线这样没有“宽度”的几何物体，填满一个平面这样有“宽度”的几何物体呢？当然，若仅仅是找到实数轴 与平面 的一个同构，这是简单的， 与 也是同构的。但“用一个直线填满一个平面”还包含着直线与平面的一些几何信息：我们并不能先将直线拆成点，再把它们撒在平面上；我们需要一根真正的线蔓延在平面中，占满其上的任何一寸空间——换言之，需要找到的同构是连续的。一种构造 Peano 曲线的方式是通过迭代，下图展现了迭代的前几步：

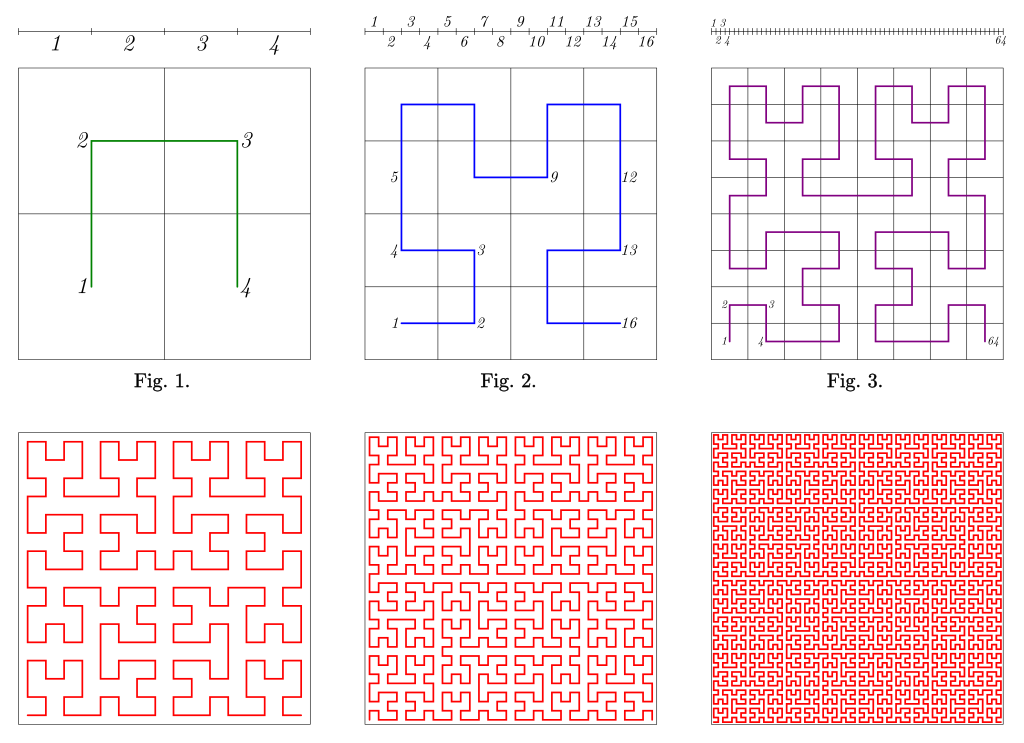如图所示的迭代是 Hilbert 给出的版本，与 Peano 最早找到的构造不完全一致，但方法是类似的。

简单但不太严谨地来说，当将上面的曲线迭代无穷次后，我们便能够得到一个填满整个正方形的曲线；若更加小心地叙述，整个过程可以用严格的数学语言表达出来。这样曲线的存在似乎挑战着我们对于几何物体“维数”的直观。

而在 Banach-Tarski 定理中，为何把一个球分解成有限份后再重组，其体积能够变成原来的两倍呢？其中一个原因便是，我们切分后的一些部分是三维欧式空间中的不可测集。尽管所有的操作，例如平移、旋转都在直观上保持几何对象体积的不变性，但我们切分的方式使得一些得到的子集并不能有效地被赋予体积（更严格地，勒贝格测度），因此“保持体积”这一说法也就无从谈起了。

事实上，当选择公理成立时，欧氏空间中就会有许许多多的勒贝格不可测集。即使是数学专业的人也不一定对选择公理的内涵十分了解，暂时我们可以将其理解为数学家们假设集合所具有的一种性质。我们将在下一个小节中更具体地谈谈选择公理以及它的推论。

反过来看，Banach-Tarski 定理的成立也表明，当选择公理成立时，我们不可能在在三维欧式空间中找到一个具有有限加性质的测度（即不相交的两个集合的测度是两个集合测度的和）使得其所有子集都是可测的——因为我们找到了一种有限分解单位球再重组使其体积加倍的方法，若其中涉及的所有子集都是可测的，这便会与有限加性质矛盾。

回过头来看，从黎曼开始走出欧式平直空间的范畴研究弯曲几何之后，人们对于“空间”或“几何”的认识都不断发生着改变。人们曾经认为几何对象所必须具有的性质，在现代数学中并不一定成立。想要真正理解 Banach-Tarski 定理，并化解其与我们脑中对几何物体直观的矛盾，我们似乎必须对”空间“和”几何“这些概念有更加深入的反思——我们将在最后回到这一点上。

现在，让我们来更加仔细地谈谈什么是选择公理。

选择公理

我们在一开始叙述 Banach-Tarski 定理时就提到，即使数学上 Banach-Tarski 定理是成立的，在现实生活中我们永远没有办法把一个苹果分成有限份再重组，得到两个和原来一模一样的苹果。这不是受目前人类的技术所限，也不是因为我们没有足够的计算能力；即使整个宇宙的能量和计算能力都为我们所用，Banach-Tarski定理所描述的现象也无法真正实现——这一限制是根本性的。这不禁让人感到更加神秘，为什么现实生活中永远无法做到的事情数学家就能声称它们存在呢？想要理解这一点，我们还得暂时跳出几何的世界，再次回到更为抽象的集合层次上来。

公理集合论的发展很大程度上是为了研究无穷的性质。想要得到一个针对无穷的严格数学理论，仅仅凭借我们脑中对集合直观的认识是远远不够的，甚至无法保持逻辑的一致性，容易导致矛盾。这之中最著名的例子便是罗素悖论。这是一个真正意义上的悖论，即它会导致自相矛盾的结论。罗素悖论挑战的是我们脑中“任何一个性质都能定义一个集合”这一朴素的观念。这也是为何在20世纪，许多数学家要花费大量的精力，利用公理化的方法尝试描述出一个严格的、一致的形式系统来刻画无穷的性质，最终才发展出了公理集合论这一数学分支。可以说，绝大部分现代数学分支都是建立在严格的集合论体系之上的。

尽管大部分公理集合论的内容非常技术化，与我们理解 Banach-Tarski 定理没有那么相关，但其中有一条公理非常重要，即为著名的选择公理。Banach-Tarski 定理的证明严格地依赖于选择公理（更确切地说，其依赖于比选择公理稍弱的一个版本）。换言之，若没有选择公理，Banach-Tarski 定理的结论也不可能成立。对选择公理严格的依赖性是我们没有办法在现实生活中实现 Banach-Tarski 定理的主要原因。

选择公理看起来是一条非常自然的公理，其内容如下：假设有一个非空集合 ，对于集合中的任意一个元素 都有另一个非空集合 ，即存在以 中的元素为角标的一族非空集合 ，则必定能够同时对所有 都选出 之中的一个元素；换言之，我们能够找到定义在 上的一个函数 ，使得对于任意 ，都有 。我们把这样的函数 称为这族集合上的一个选择函数，选择公理即是说当有一族非空集合时，其上一定存在一个选择函数。

选择公理尽管被称为一条公理，但事实上它是集合论当中的一条假设。它看起来非常自然：既然每个集合 都非空，我们自然能够在所有的这些集合中都选出一个元素，构成一个函数。但事实上，如果这族集合 不具备任何其他的信息，则当 是一个无穷集合时，我们几乎没有任何具体地写下这样一个函数，因为我们无法真正地完成无穷多次选择，只能假设它们存在。

为了说明这一点，我们考虑一个具体的例子：令集合 是自然数集合 ，而对于任何的自然数 ，我们都有同一个集合 。显然，这一族集合 上的一个选择函数就等价于一个函数 。即使不依赖于选择公理，我们也能直接地写下很多个这样的选择函数。例如对于任意 ，我们都有一个常函数 把每一个自然数 映射到 。

更直观地来说，我们可以把这样的一个选择函数 和 区间上的一个实数等价起来，把 理解为这一实数小数点后第 位上的值。因此，对于这一族集合，其上选择函数的个数应该与 区间内实数的个数是一样的，是不可数的。但事实上，我们真正能写下的选择函数的个数只有可数个。

我们可以从信息的角度来理解这一点。要描述一个从 到 的函数 ，本质上需要无穷多的信息，这是因为我们要对所有的自然数 都描述其函数值 是多少。但显然，没有无穷多的信息资源供我们使用。因此，在现实生活中能够写下的任何一个实数必定依赖一个有限的算法来告诉我们其每一位的值是多少。比如之前提到的常函数，就可以用下面这一段简单的代码来表示它：

throw input;
return i.
 

这段程序对于任何输入，其都输出 ，这就是常函数 的一个有限表示。其他我们熟知的实数，例如 ，其尽管不如 一样具有非常简单的规律，但我们仍可以写下一段很简单的代码来计算 任意一位的值。事实上，有一个专门的数学分支，称为 Kolmogorov 复杂性，专门通过描述一个物体的难易程度来研究数学对象的复杂性。例如，如果计算 的程序比我们上面写下的两行代码要长，那么 的 Kolmogorov 复杂度就比 要大。不过这不是本文的重点。

借助这种信息的视角想说明的是，对于绝大部分实数，其没有这样有限的算法来表示它，一个简单的大小比较就可以认识到这一点： 中所有的实数是不可数的，但所有程序的集合是可数的（这是由于任何一段代码必须是有限长的）。这一点表明， 区间中具有有限表示实数的数量远远低于其他实数的数量——前者在 区间中仅仅为一零测集。尽管任何接触数学的人都在使用 区间，觉得它的性质很平凡，但若仔细来看， 区间真的就像一个黑洞一般，对于里面包含的绝大多数实数，我们穷尽宇宙的资源也无法对它们真正了解——如果我们认同宇宙中原子的数量是有限的话。尽管使用选择公理我们能够保证其他这些实数存在，但我们能够真正写下的，只是其中很少的一部分。

这种在使用选择公理时数学假设的存在性，与我们在现实生活中能够实实在在构造出的对象之间的不一致，便是我们觉得 Banach-Tarski 定理违背常识背后的一个很重要的因素。前面我们提到，Banach-Tarski 定理的证明严格地依赖于选择公理。更为具体的，把一个球分解成有限份再重组成两个一模一样的球，若要完成这件事，这个分割的构造必须依赖选择公理，而没有办法直接地写出。这种分解的方式只在数学上假设了其存在，但在现实生活中是无法完成的。这是我们说尽管 Banach-Tarski 定理成立，你也无法真正把一个苹果切成有限份再拼凑成两个一模一样苹果的原因。因此，当你真的身临绝境，还是不要钻研数学了，好好学习农业，精通果树种植技术才是务实的选择！

自由群

Banach-Tarski 定理能够“凭空捏造”出多一倍体积背后的原因竟来自于一个特殊的代数结构：，由两个元素生成的自由群。从代数的角度， 的每个元素可以被认为是由 , , 和 构成的有限序列（允许长度为0的序列存在，这就是 的单位元），同时要求这些序列必须处于最简形式，即我们必须用空序列替换掉序列中出现的所有 , 或 , 。例如， 或 便是 中的两个元素。下面展示了 的 Cayley 图：

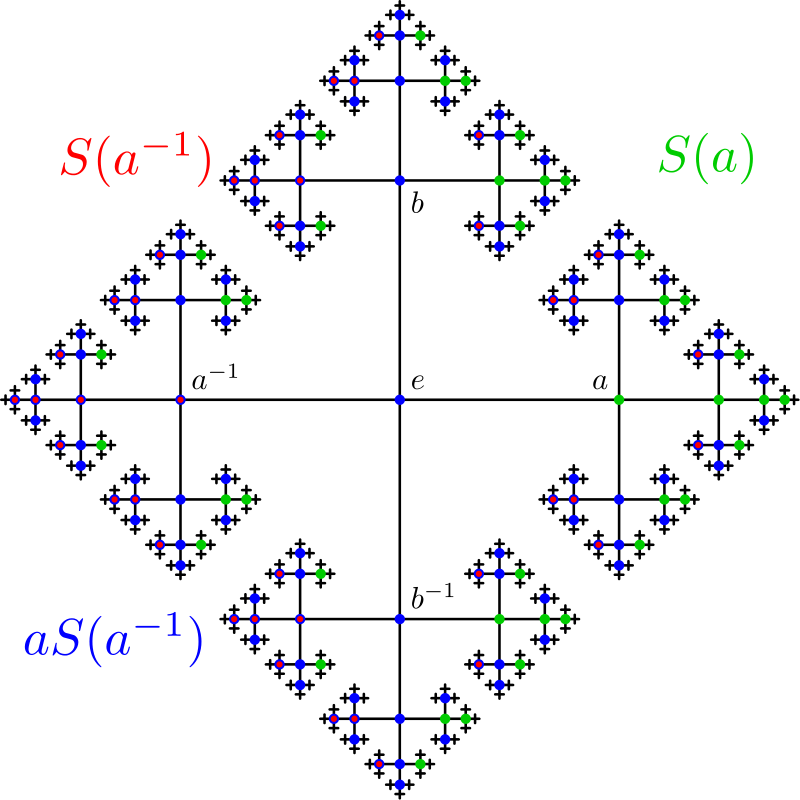
若令 表示 中那些以 开头的元素，同理定义 , 和 ，则显然根据定义，

在上图中，则可直观地看到 是由一个中心点和四个枝叶构成的。但若考虑 的一个变换 ，即把 中的每一个元素都在左边乘上 得到的集合，稍加思考我们便知

这是因为，根据我们对 和 的定义， 后紧跟的元素可以为 , 或 中的任何一个，只是不能为 ；当在它左边乘上 后，其与开始的第一个 相互抵消，剩下后面的部分。在上图中我们也可以直观地看到这一点：左侧的那一叶若等比放大后事实上与上、左、下这三叶合起来是同构的。因此，我们只用四叶中的两叶便能够还原出 ：

同理，我们用剩下的两叶也能够还原出整个 ，

这一点听起来就和 Banach-Tarski 定理所表述的非常接近了： 被 分解为了4叶，两两组合，再通过变换拼凑成了两个 。事实上，Banach-Tarski 定理的证明，在代数结构上就需在三维空间的刚性变换群中找到一个与 同构的子群，再依据上述 的切分和重构来把三维空间中的球分成有限份。同时，Banach-Tarski 定理要求空间的维数大于等于3也是基于此：在一维和二维空间中，由于它们的刚性变换群较小，并不包含与 同构的子群，因此 Banach-Tarski 定理的构造并不适用于这些情况。

具体构造

终于，讲完上述的所有要素，我们可以来叙述 Banach-Tarski 定理的证明了。需要做如下几步：

第一步 首先我们需要在三维空间的刚性变换群中找到一个与 同构的子群。构造这个子群的方式很简单，可以利用绕两个相互垂直的轴的旋转变换获得。分别考虑绕 -轴和 -轴旋转一个 -角度的变换，也记这两个变换为 和 ；要求 是一个无理数，这样能够保证旋转任意多次不会回到原点，即对于任意 , 和 不会是单位元。再加上 -轴和 -轴是相互独立的，这样能够保证由 和 生成的群是自由的，即其与 同构。我们记这个群为 。

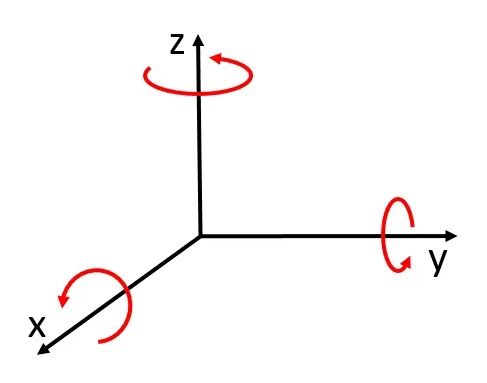
第二步 下面我们就可以来着手构造所需的有限划分。为了简单起见，我们可以先考虑球的表面 。显然， 中的任意一个元素作用在 上会是其自己到自己的一个旋转变换，而我们考虑 在 作用下的所有轨道（orbit）。对于 上的任意一个点 ，其所在的轨道是由如下这些点构成的集合，

即 所在的轨道是所有那些在 作用下 能够“到达”的点的集合。在 的作用下，整个 便被划分成了许许多多互不相交的轨道。由于每个轨道中包含的点的个数都是可数的，而整个球面中包含的点的个数是不可数的，因此所有轨道的数目也必定是不可数的。利用选择公理，我们能够在所有轨道中都选出一个代表元，构成一个集合 。值得注意的是，如前所述，集合 的构造严格地依赖于选择公理，且在球面上的分布是极其不规则的，因为我们没有办法用任何一段有限的算法给出 在球面上的分布——不然就可以不用选择公理来构造 了。对 Banach-Tarski 定理证明最重要的是，集合 具有这样的性质：对于球面上的任意一点，存在集合 中唯一的一个元素 ，使得 在 中一个变换的作用下能够到达这一点。这个命题成立是由于球面上任意一点都属于且仅属于一个唯一的轨道。

第三步 当构造好 后，我们便可以利用前面对 所做的划分来构造球面 的一个划分。由于 和 是同构的，我们仍然使用 等记号来表示对应的 的子集。定义如下这些集合：

其中 代表在 中的变换作用后 中的点到达的所有点构成的集合，

的定义如下：。这里 和 并没有直接的定义为 和 仅仅是因为那样定义后，这四部分重组后还会多出来一个 。其实在了解了 的分解后，上面具体划分的定义没有那样重要，读者也能很方便地找到其他划分的方式。但最终，最重要的性质是，当我们旋转其中一个划分后，和 类似，它能够变成另外三个部分的并：

因此，这使得我们有 , 。即我们把 分解成4份，把其中两份进行一个旋转变换再和另外两份拼起来，就能得到两个 球面。

第四步 要把 3 中的构造推广到实心球体上是简单的，只需挖去中心点，3 中的构造便对任意半径的球面都成立。因此，我们只需把 中的点看作是从原点（不包含原点）到其自身的一根半开半闭的线段，3 中的构造就可以覆盖单位球中除原点以外的所有点了！因此，我们最终得到的单位球的5个划分便是 上的 , , 和 “拉长”后的四个集合和原点 构成的集合。把原点留在原地不动，按照 3 中的方式重组其他四个集合，我们便得到了 Banach-Tarski 定理中所求的构造！

证明之后

回到主题 Banach-Tarski 定理，给出了它的证明后数学的工作就完成了吗？并不如此。我们知道了它的证明，但仍不能完全解决我们最开始听到这个命题后所产生的怀疑。现在，就让我们回过头来重新想想它被称为“悖论”的原因。

如我们一直强调的那样，Banach-Tarski 的结论是一个定理，之所以在很多情况下称其为悖论，是因为它的结论与我们的几何直观并不相符。在这种情况下，我们至少有两种可能的选择：接受现有描述几何对象的框架，调整我们的几何直观；或者寻找一个新的描述几何对象的框架，使得 Banach-Tarski 定理或类似的现象能够得到一个更加直观地解释。

在大多数情况下，人们都会采取第一种策略，因为第二种路径涉及研究范式的转变，是一个更加浩大的工程。但这并不表示第一种进路就是最自然的处理方式。在 Banach-Tarski 定理中，我们得到的球面 的划分是非常复杂的，其中 , , , 这四个子集都无法被直接的描述，因为它们的存在性严格地依赖于选择公理。直观地来看，这些集合就像是在球面上随机地点了四种不同颜色的点，毫无规则可言。从何种意义上我们能够将这些子集看作几何对象呢？

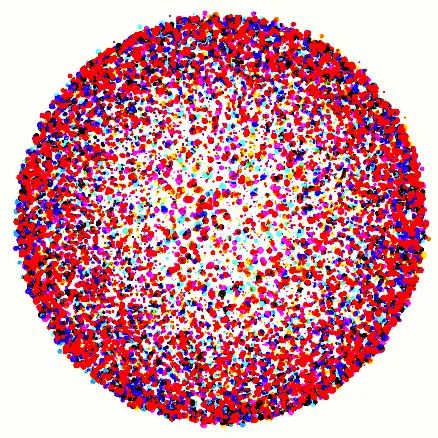
这就涉及到我们对几何的理解。现代数学对几何空间采取了一种“还原”的理解方式：几何对象都是由点构成的，其几何信息反映在这些点“粘合”起来的方式，例如其上的拓扑或测度。在这样的看法下，上面提到的这四个集合 , , , 都可以看作是欧氏空间的子集被赋予子集拓扑，它们均为 的稠密子集。但如之前所述，这些集合作为欧式空间的子集都是不可测的。

但几何空间的性质真的可以完全被还原成它所包含的点的性质吗？我们能不能直接地描述一个几何空间的性质而不借助构成它的点呢？若回到古希腊时代，对这个问题的答案应该是肯定的，且我们对几何对象的理解也定与现在不尽相同。那时，尽管直线和平面中都包含很多个点，但古希腊的数学家们并不倾向于把直线或平面理解成由许多点构造而成，而是将其自身看待为一个独立的几何对象来理解。

现代数学便有一个分支，以此为出发点来研究几何物体。为了突出“点”在这个进路中所具有的次要地位，在英文中它被称为 point-less topology（拓扑学大家 Peter Johnstone 在1983年写过一篇有名的文章 The Point of Point-less Topology），在中文世界对这一数学分支的翻译和资料都较少，或许可直译为无点拓扑或意译为直接拓扑（当然，这样的译法不具有权威性）。顾名思义，在直接拓扑中，定义几何对象的方式是直接从其拓扑所具有的几何信息出发，而一个空间中点的概念则是随后根据其几何信息构造而成的。特别的，直接拓扑扩充了现有几何空间的概念，因为其内存在没有任何点的非平凡几何对象。

若采取直接拓扑的进路，则欧氏空间中任何一个子集都会是可测的，且对于那些在经典测度论中的可测集，两种方式所定义的测度是一样的。从这个角度来看，直接拓扑或许更符合我们对几何对象直观的理解。

那又怎样解释 Banach-Tarski “悖论”呢？前面提到，根据直接拓扑的哲学，空间的点并不能完全包含空间所有的几何信息。在直接拓扑中的四个子集尽管没有相交的点，但并不代表它们作为几何对象并不相交！根据前面的图我们也可看出，这四个子集在球面上水乳交融，难以区分彼此——事实上，由于它们是用选择公理构造而成的，我们也的确没有一个有效的办法来区分球面上的一个点到底是在哪个子集中。这个事实是这四个子集的交在直接拓扑中具有非零测度的重要原因！由于在直接拓扑中，这四个点的交本身就具有非零的体积，因此把它们拆开后再重组成两个和原来一模一样的球也就不足为奇啦！Banach-Tarski 定理也就不再具有“悖论”的性质了。

结语

事实上，直接拓扑的进路能够极大地降低我们对选择公理的依赖，使得我们不再使用那些选择公理假设其存在却永远无法直接判定的数学对象。因此，直接拓扑和构造主义数学（constructive mathematics）也有很深的联系。不过碍于篇幅，没有办法在这篇文章中向大家介绍更多有关直接拓扑的内容了，就留到下次吧！

在本文的最后为大家介绍直接拓扑的内容，并不是想说明直接拓扑的进路就构成了我们对 Banach-Tarski 定理或是对几何空间最终的理解。而只是想强调，数学并不是一件非黑即白的事业，其远远不局限于对一个命题的证明，或者解决一个具体的问题。更为重要的，是要找到更为合适的数学语言，使得我们看待问题的方式更加自然更符合直观。当我们找到一个好的数学框架，许多问题往往就迎刃而解了。在两种不同的框架下对 Banach-Tarski 定理的理解便是一个很好的例子。

数学的使命从来不仅仅是言说真理——真的命题其实随处可见，但我们不会见到将形如“如果 1+1 = 2 那么 3 + 3 = 6”或“如果 1+1 = 3 那么 2+2 = 3” 这样逻辑上为真但毫无意义的命题收集成册的数学书。数学对真理是有选择的，它总是以或审美或应用的角度来阐述那些它认为“重要”的真理。在数学中，言说哪些真理、如何言说真理或从什么角度言说真理才是更长远的问题——数学是人类的创造，是一门艺术，和人类的审美息息相关，而不仅仅是对真理的发现。‍

‍本文原文发表于“水木逻辑”公众号，经作者重新修订发表于返朴。