译者按

从1911年的首届会议开始，索尔维物理学会议就一直对量子物理的发展起着推动作用。
 

今年5月，第28届索尔维会议在布鲁塞尔召开，会议主题为“量子信息的物理”。量子计算先驱彼得·肖尔出席会议并做了报告。这是肖尔的报告文稿，将收入会议文集中。

蒙索尔维国际物理学化学研究会慷慨允诺，我们得以把这篇文章翻译刊载出来。
 

这是文章的上半段，讲述了上世纪80、90年代期间，量子计算起步阶段学界的一些趣事：比如费曼对是否应该“探讨自然成因”前后不同的看法、他在“负概率”一文中未提及作为动机的贝尔定律；肖尔受“西蒙问题”的启发解决了离散对数问题，而他之后关于离散对数问题的讲座被“以讹传讹”为解决了因数分解问题，以及物理学家知道他这一工作的始末......

撰文 | 彼得·肖尔（美国麻省理工学院应用数学系教授，Shor算法提出者）

翻译 | 左芬（博士，上海微观纪元数字科技有限公司）

彼得·肖尔丨来源：麻省理工大学

这个演讲最初是为了纪念1981年在恩迪科特大楼举办的物理与计算会议的40周年而准备的，所以我觉得我应该从1981年说起。

我那时是加州理工的大四学生，所以当费曼为恩迪科特大楼会议准备主题发言时我已经在那儿了，而那次发言成为了最早仔细审视量子计算的几次尝试之一。

我在加州理工的时候什么消息也没听到，事实上我很久以后才读到费曼的文章。不过我倒是想提一下我听他在加州理工的另一个讲座，因为那个讲座表明他那时正在思考物理学基础方面的问题。

费曼的报告是关于负概率的。

在报告开头，他解释说他一直在思考贝尔定理，因为它说明量子物理不可能是一种局域的、实在的隐变量理论。
这就意味着，量子力学的任何解释要么要求非局域性，要么要求非实在性（这里局域性意味着信息不能超光速传播，而实在性意味着你能测量的东西对应着粒子的具体性质）。

费曼解释说他所做的就是仔细审查证明贝尔定理用到的前提，看里面是否存在隐藏的假设。

他确实找到了一个——那就是所有概率都必须在0和1之间。

这并不像初听起来那么古怪——简谐振子的维格纳函数的行为就恰好这样，而且费曼也提到了这一点。

他接着展示了他发现的关于负概率的一些结果；报告的这部分内容我记得不是很清楚了。

更早的时候，在1964年的系列讲座上，费曼曾说：

“我来告诉你大自然到底是怎样的。如果你直接接受她表现出来的样子，你会发现她是迷人的、令人愉快的。如果你能忍住，就不要老是问自己，‘它怎么会是那样子的呢？’，因为你会‘深陷泥潭’，进入到一个没人能逃脱的死胡同中。没人知道它为何那样。”

但是这时，15年后，他却在探讨自然为何会是这样的一个可能的原由。从这里你可以看出来费曼并没有采纳他自己的建议。

当然，也许他的建议不是给终身教授，而是给研究生们的；对他们来说，那可能是很好的建议——在量子力学的基础上得出新的、重大的结果是相当难的，所以它对研究生来说不是一个好的课题。

几年后的1983年，费曼把报告中的一些想法写了下来，写成了一篇叫做“负概率”的文章，但文章在那好多年后才得以发表。

那篇文章有趣的地方在于，它并没有提到作为动机的贝尔定理。

他的文章首先讨论了维格纳函数，这些函数确实给出了负值的概率。费曼接着将维格纳函数推广到自旋系统的量子比特。

而费曼在他的报告中讲述的原始动机已经被消除量子场论中的无穷大所取代。因此想必费曼的原始想法并不奏效——他没能利用负概率解决爱因斯坦-波多尔斯基-罗森（EPR）悖论。

我不知道究竟是什么导致了动机的改变。难道他觉得试图找出一种更好的方式来理解贝尔定理这个动机太丢人了，因为这牵涉到量子力学的基础，所以他想出了一个更加体面的？或者是还有别的什么原因？

我还想说说那个年代另一篇有趣的文章。

1985年，大卫·多伊奇写了一篇关于量子图灵机、量子计算以及量子邱奇-图灵论题的文章。

多伊奇的动机部分源自于量子力学的基础——他宣称有了量子计算机，就有可能检验量子力学的埃弗里特（多世界）解释。
他在文章中说：

对这些性质的直观说明给埃弗里特之外的所有量子理论解释带来了无法承受的压力。

我想表明在这一点上我并不认同他，尽管他一直没有改变观念。

1985年，费曼写了他1982年文章的续篇，其中给出了如何建造量子计算机的详尽得多的提议。不过这一提议仍然不太切实可行，因为它在构建初态和跃迁振幅上要求极其高的精度。
作为一个有趣的旁注，我想指出当大卫·多伊奇和理查德·费曼在考虑量子计算时，他们都在思考着量子基础。我的直觉是这很重要。
如果你认同了大卫·梅尔曼版本的哥本哈根解释——“闭上嘴去算吧”——那么你就不会去思考量子的古怪性，这样你可能也就不会去思考量子古怪性的可能用途。

在加州理工，我学了一些物理课程，但主修数学。

我接着去了麻省理工的应用数学研究生院，在那里研究数学与计算机科学的交叉部分，并最终在贝尔实验室找了一份数学和计算机科学方面的工作。

我第一次听说量子信息是在查理·本内特在贝尔实验室做的一次报告上，他在报告里讲述了BB84量子密钥分发协议（译注：该协议由Bennett与Brassard于1984年提出，故名）。我不记得那是哪一年了，不过肯定是在80年代末期。

我记得我对他的报告非常着迷，还思考过一阵查理提出的一个未解难题。这个难题就是你能否严格证明BB84协议是安全的。

在思考过程中，我完全不清楚如何将量子力学表述成某种数学形式，以便严格证明该协议是安全的。所以我放弃了那个问题。

说起来有点好笑，到了2000年，在我熟知了量子计算、量子信息和量子纠错码之后，约翰·普雷斯基尔和我倒是想到了BB84安全的一种简单证明方式。

这已经是BB84安全性的第三种证明，不过前两种证明，分别由迈耶斯和比哈姆等人完成，相当复杂。

我仔细读了迈耶斯的证明并意识到CSS编码（译注：即Calderbank-Shor-Steane编码，后文有详细介绍）隐含在其中，而如果使用这些编码，你可以得到一种简单得多的证明。

在本内特在贝尔实验室的报告之后，我再也没想起过量子计算，直到1992年优曼许·沃兹内尼到贝尔实验室来做报告，讲述他和伊桑·伯恩斯坦关于量子图灵机的文章。

这篇文章后来发表在1993年6月的计算理论研讨会（STOC）上，最负盛名的两个理论计算机科学会议之一。

我对那个报告极为着迷，而且我可能比其他计算机科学家理解得都深一些，因为我在大学时学过一些物理。

伯恩斯坦和沃兹内尼给出了一个精心设计的问题使得量子计算机看起来可以做得更好，但我对那个问题不是太满意。

于是我开始思考是否可以用量子计算机更有效地解决一个实际问题。

我并没能真正取得进展，直到我读到丹·西蒙的文章。

他在文章里用量子计算机算法解决了一个人为问题，“西蒙问题”，并且比最好的经典算法还要好得多。

我会读到这篇文章是因为我在1994年STOC会议的项目委员会里，而委员会拒收了那篇文章（尽管我已争取了）。

我听说丹·西蒙的出发点是想证明数字计算机不再比量子计算机强大，但他最终找到一个问题显示了相反的结果。

西蒙用到了一个二进制矢量空间上的傅里叶变换来找出该矢量空间上一个函数的周期。

我知道傅里叶变换对寻找周期有帮助，而且我知道离散对数问题跟周期性有关，所以我开始寻求在量子计算机上解决离散对数问题的方法。

离散对数问题是一个有名的难题，如果你解决了它，就可以破解一些公钥加密系统。

西蒙算法和离散对数问题中的周期寻找的差异在于，对于西蒙问题，你需要在n-维超立方体上找到一个函数的周期，而对于离散对数问题，你需要在P-1×P-1环面上寻找周期。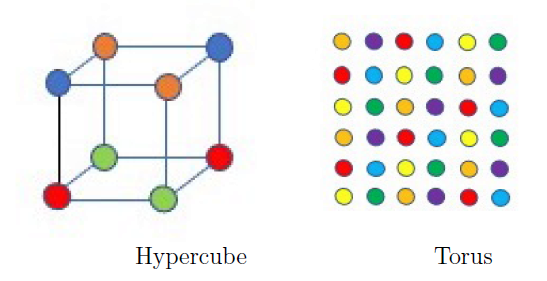

左图，超立方体顶点上周期寻找的例子。这里的周期是（1,1,0）。右图，2-维环面上周期寻找的例子。这里的周期是（2,1）。

如何从一个高维超立方体上的周期寻找转到一个大的环面上的周期寻找，这是完全不清楚的。对这些你需要不同的量子傅里叶变换。
我最先做到的是在一种特殊情况下解决了离散对数问题，而这种情况已经被经典计算机在多项式时间内解决了。
尽管这并没有真正给出新东西，但算法跟经典算法是完全不同的，所以给了我很大的鼓舞，让我去继续努力并最终解决了一般情况。
我从特殊情况到一般情况的顿悟就是认识到对于一般情况，我并不需要采用模P-1的傅里叶变换；我只需要模一个比P-1稍大一点的数就可以了。

我并没有告诉任何人我在致力于离散对数问题，因为我觉得实在没啥把握。

在我1994年4月解决它之后，我告诉了一些认识和合作过的人，包括我的老板大卫·约翰逊，以及贝尔实验室的一个同事，杰夫·拉加里亚斯，他验证了我的算法是对的。事实上，不完全对——杰夫找出了一个小错误，很容易就改好了。

之后，大卫·约翰逊建议我在亨利·朗道研讨班上就此做一个报告。

亨利·朗道研讨班每周二举行，并且听众极其活跃——他们不断打断报告人提问，所以有点吓人。我记得有一次，报告人就没能翻到第二张幻灯片。

不管怎样，我就如何在量子计算机上解决离散对数做了一个报告，并且还算顺利。

那周晚些时候，我把因数分解问题也解决了。离散对数和因数分解之间有着奇怪的联系。并没有一个公式告诉你，如何将针对其中一个问题的算法应用到另一个上面去。

但是，每次有人发现其中一个问题的改进算法，人们都相当快地想出了另一个问题的相似解法。

这一次也不例外——知道了离散对数算法，很容易就找到了因数分解算法。

那个周末，我得了重感冒在家，优曼许·沃兹内尼打电话给我说“我听说你可以用量子计算机有效分解因数”。

这有点出人意料，原因有很多。首先，这表明我周二报告的流言已经传播到优曼许那里了。其次，报告是关于离散对数的，但等流言到达优曼许那里时，它们已经变成了因数分解（这有点像电话游戏，也叫传话游戏，其中一个小道消息从一个玩家传到下一个，并且沿途改变）。

不过幸运的是，我同时也解决了因数分解问题，所以可以向优曼许解释因数分解算法，而不用告诉他信息有误。

在那之后，消息像野火一样蔓延开去。

四月末哥伦比亚大学有一个（关于理论计算机科学的）理论日。查理·本内特、约翰·斯莫林和我约好在那会面，然后我向他们解释了这个算法。

如果我记得没错，本内特给我解释了他新近的隐形传态协议，以及新近的伊利泽-威德曼炸弹测试协议。很明显量子信息这一主题的时代已然来临。

我被紧急邀请去五月初在康奈尔举办的算法数论讨论会上做了专题讲座。

五月中旬在圣塔菲有个关于量子力学的会议；我去不了，不过优曼许在会上展示了我的算法。阿图尔·埃克特和大卫·乔萨写了一篇文章向物理学家们解释我的算法，并且阿图尔·埃克特在那年八月科罗拉多州博尔德举办的原子物理会议上就此做了报告。

这就是许多物理学家如何得知它的，正如你在这次会议上从大卫·瓦恩兰的报告里听说的那样。在此期间，我收到了许多杂志的采访请求，以及许多人索要文章副本的请求。（我在文章彻底完成之前就开始寄出去，但这可能是个失误，因为在我纠正了文章中的错误之后很久，还有人问关于早期初稿中错误的问题。）

那年八月，美国国家标准技术研究所（NIST）在马里兰州盖瑟斯堡组织了一次会议，是专为因数分解算法的发现而组织的，并且聚焦在量子计算上。

十月，在意大利都灵有一个量子计算的研讨会，那其实是一个系列会议里的第二或第三届。这个会最初只有几个人参加，之后与会人数逐年增长，直到超出了瓜里诺庄园酒店的会议设施容量，于是被终止了。

94年德克萨斯的物理与计算会议是1981年恩迪科特大楼会议的后续（一共举办了三届后续会议，分别在92年、94年和96年），我在那做了报告。

紧接着几天后，我在新墨西哥圣塔菲的计算机科学基础（FOCS）会议上讲述了我的文章，并且在会议文集里发表了。
 

原文链接：

The Early Days of Quantum Computation，Peter W. Shor, arxiv:2208.09964, https://arxiv.org/abs/2208.09964

本文经授权转载自微信公众号“中国信息协会量子信息分会”。