撰文 | 张伟伟

一个坡度较陡的深坑，男子从坑底沿着倾斜的内壁奔跑，竟有了飞檐走壁的本领！不过，就在即将要跑出坑道的时候，男子停止了奔跑，希望用手去抓住坑道的边缘，此时墙壁就像失去了摩擦，顺着墙壁滑了下去。为什么跑起来就可以站在墙壁上，一停就滑下去了呢？从结果来看，奔跑可以增加摩擦力，一旦停止摩擦力缺失。考虑斜面上的摩擦力，如图1所示。设有倾角为θ的斜面，其上放置重为mg的物块。以物块为研究对象，对其进行受力分析 (将其视为质点)，物块共受3个力的作用：1重力mg；2斜面支撑力N; 3斜面摩擦力f。

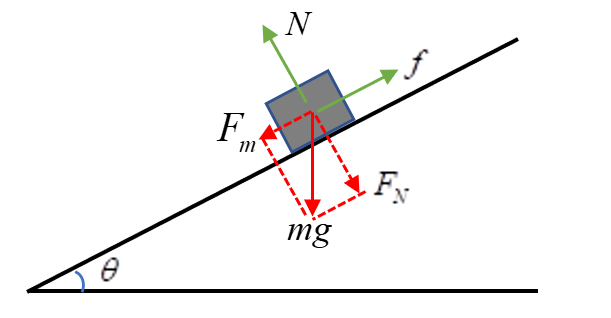
图1 斜面上物块的受力分析将重力分解为垂直斜面的分力

目测视频中的斜面倾角在60o左右，超过了临界倾斜角度，人也就无法静止站立在坑道内壁上。如果希望依靠自身“走”出坑道，必须增加摩擦力。由式(2)可知，摩擦力有两个因素有关，一是摩擦系数，二是正压力。摩擦系数由材料决定，由于男子的鞋与墙壁的材料已经确定，摩擦系数确定，因此，只能通过改变正压力来增加摩擦力。当男子沿着坑道奔跑时，如图2(a)所示，其运动可视为绕轴旋转。当人做旋转运动时，必须有足够的向心力（改变运动方向），这里向心力只能依靠墙壁提供。根据作用力与反作用力，墙壁给人提供向心力的同时，人对坑道内壁的正压力也就相应的增加，这就是与静止状态相比所增加的正压力。

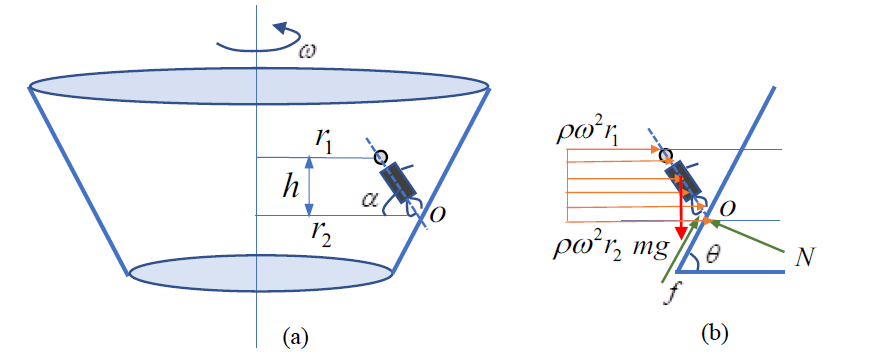
图2 男子沿内壁奔跑示意图及受力分析图

以人为研究对象，利用达朗贝尔原理，画出人在奔跑时的受力特点，如图2(b)所示。这里，摩擦力f和支撑力N作用于人与斜面的接触点o，重力可以等效为作用于人的重心，设重心在人高度的2/3处。图中的分布力，为人在奔跑时产生离心力（虚拟力，由向心力等效得出），这是人保持平衡的关键。由于人的身子具有一定的倾角，所以从头部到脚的旋转半径并非常数。为了便于描述，我们设人的质量沿身高平均分布，在高度方向的平均密度为ρ=m/h，假定头顶的旋转半径为r1，脚的旋转半径为r2，离心力满足梯形分布，其它参数如图所示。

上述方程组包含三个未知数：1摩擦力f；2斜面上的压力N；3角速度ω（静止状态下，摩擦力不一定等于最大静摩擦力）。求解未知数，得

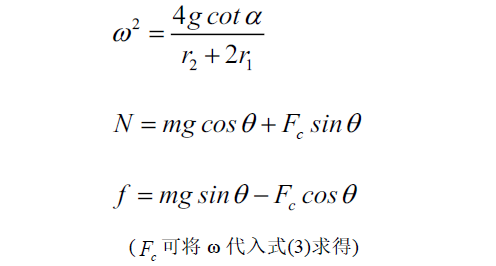
由上述解答可知，人以角速度ω奔跑时，人在斜面上可产生的正压力为N，根据最大静摩擦力的求解fmax=μN，奔跑时就可以提供比静止时更大的摩擦力。此外，还可以看到，角速度的解与质量无关，旋转半径是主要影响因素，想办法让旋转半径大一些，更在较小的角速度下满足平衡条件。跑出坑道的力学秘诀就在于借助离心力增大墙壁的摩擦力，不要停，直到你成功的跑出坑道为止：

本文经授权转载自微信公众号“力学酒吧”。