
玻璃悖论
玻璃是远离平衡态的材料,可以通过避免热力学转变为有序的晶体结构来制备。理论上讲,如果等待足够长时间,玻璃最终将会达到它真正的平衡态——晶体。这里,我们在图中展示了几个从古至今仍然保持玻璃态的例子:埃及的陶罐(最右边)大约有2500年的历史;2000万年前的琥珀玻璃可能包含了恐龙时代的生命痕迹(左下),就像好莱坞大片中流行的那样,研究人员可以借此了解较长的老化时间如何影响玻璃性能[1];许多早期文明用黑曜石制成箭头(左上)和其他工具(黑曜石是一种天然存在的火山玻璃,可以保持玻璃态7500万年而不结晶);阿波罗15号宇航员从月球带回了小玻璃珠(上中),它们的历史超过30亿年,是地球上最古老的玻璃。从这些例子,我们可以看出玻璃可以很容易实现类似于晶体的长期亚稳态。
考虑到玻璃的非平衡特性,它们的长期稳定性可能令人惊讶。这种稳定性,以及它们组分的多样性,使得玻璃适合作为核废料的储存介质(参见文章lan Pegg,PYHSICS TODAY, February 2015, page 33)。玻璃在比玻璃化转变温度低得多的温度下进行储存可以提高玻璃的稳定性,其中,低温减缓了分子重排,从而抑制了晶体的成核和生长。
环境因素对玻璃的稳定性也很重要。地质玻璃经常因接触水而结晶;氧化环境有可能改变玻璃的化学性质,并导致结晶;在地球上,构造板块缓慢而持续的运动将地质玻璃再循环成其他材料;考虑到月球的温度和环境,月球可以说是玻璃的完美家园。
撰文 | Ludovic Berthier(法国蒙彼利埃大学国家科学研究中心主任)、Mark Ediger(威斯康星大学麦迪逊分校化学系教授)
翻译 | 付洋(理论物理所2020级博士生)
虽然人类已经有超过3000年制作玻璃的历史,但对于玻璃基础物理的理解仍在不断深入研究中。
制作玻璃最简单的方法是将材料从液态迅速降温到不再发生晶相成核和生长的状态。在材料不形成晶体的情况下,随着温度的降低,过冷水粒子的运动急剧减缓。材料降温时,粘度降低,玻璃吹制工人利用了这种运动减缓的特点来为材料塑形。
当温度进一步降低时,分子重排的时间尺度变得较长,以至于系统相对于过冷液体已经处于非平衡态。材料停止流动,成为玻璃[2],此时的温度被称为玻璃化转变温度 (glass transition temperature)。
玻璃和其他无定形固体可以由原子、简单有机分子、较大分子(例如聚合物)或胶体粒子的集合构成。甚至像沙堆、剃须膏一样的宏观成分,也可能形成类似于分子和原子玻璃的刚性无序粒子集合。不同类型材料的玻璃形成过程展现出显著的共性,比如随着温度的降低,局部结构的微小变化伴随着粘度的显著变化。
对于许多材料,制备玻璃并不困难,每分钟几个开尔文的降温速率足以避免结晶。然而,对于晶体成核效率高的材料,例如简单金属或具有高对称性的分子,就很难制备出玻璃了。此时,如果想要制备玻璃,就需要进行超快降温。然而,在某些情况下,即使降温速率高达 K/s,也可能无法制备出玻璃。
就分子组成而言,玻璃状材料似乎是液态在低温下的延续。如图1所示,粒子的构型与过冷液体的无序结构非常相似。然而,玻璃并不易发生形变,又因此构成了一种固体物质。固态性质 (solidity),通常作为周期性晶体的平移对称性破缺的直接结果而出现在固体物理教科书中,也可以存在于非周期性结构中。一些分子在 以下仍然可以发生重排并流动,但极为缓慢,并且随着的温度降低而减缓。
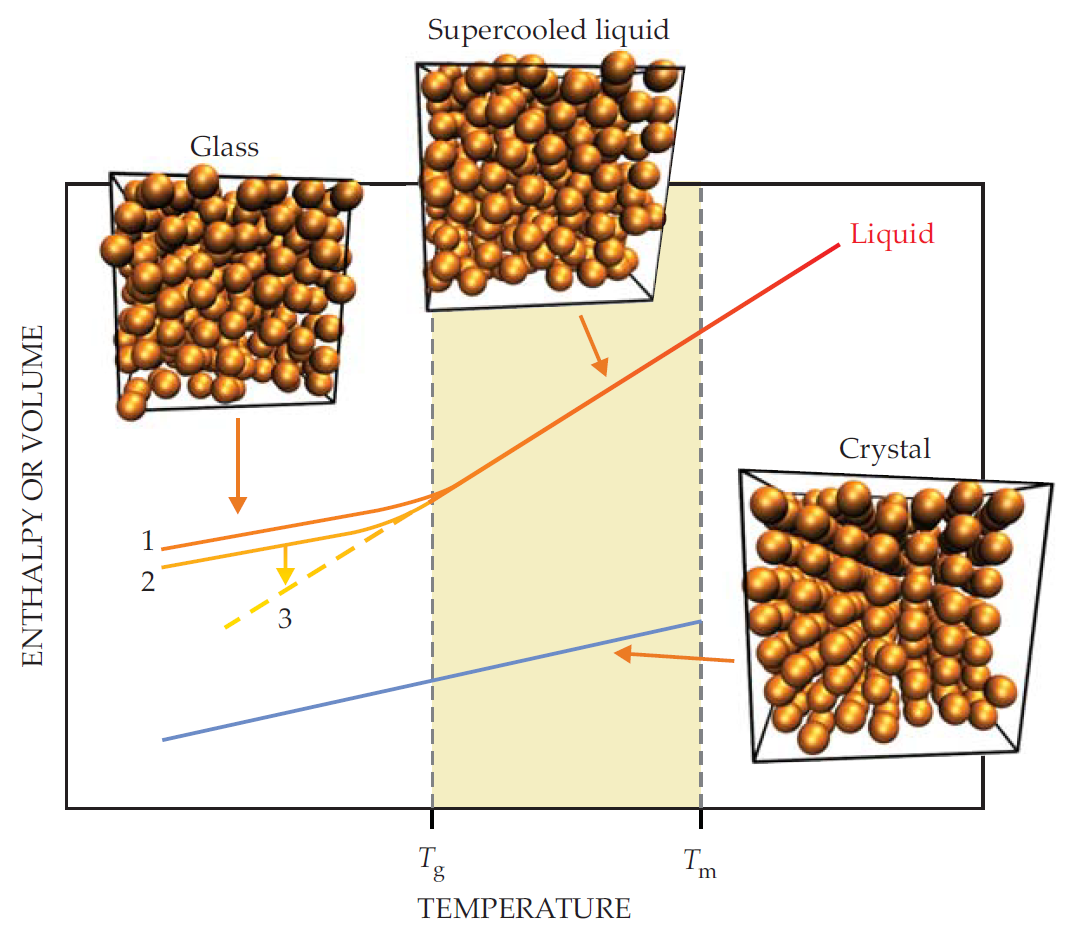
图 1: 你能找到玻璃吗?当液体降温到熔点 以下时,液体的焓或摩尔体积展示了三种不同玻璃的产生。如果未发生结晶,可以从液体降温得到玻璃(玻璃1);更为缓慢的降温会产生较致密的玻璃(玻璃2);在玻璃化转变温度 以下进行等温老化会产生更致密的玻璃(玻璃3)。分子动力学计算模拟展示了玻璃、过冷液体及晶体的典型粒子构型。
作为宏观各向同性固体,玻璃是许多应用的最佳材料,例如光纤和窗户。与玻璃不同,较大晶体的的晶界可以散射光线,因而体现出宏观各向异性。此外,可以通过充分改变玻璃成分来优化性能。宏观的各向同性和组分的灵活性源于玻璃的局部无序液体状结构。
从基础研究的角度来看,玻璃也是一种非常迷人的材料,因为它代表了物质的非平衡无序状态。从热力学相变的角度理解玻璃,这是至今尚未被解决的激动人心的挑战[3]。与晶体相比,玻璃所带来的困难存在本质差异。这是由于,晶体有着完美有序结构,对应着唯一的自由能最小值,而玻璃则呈现出大量的、同样无序的、不完美结构。降温之后,对于玻璃的复杂自由能景观的探索就减缓了,系统最终必须从众多可用的玻璃状态中选择其中一个。系统的末态是一个巨大的可能无序状态库中的一个状态,每一个状态都代表了一个局部自由能极小值。
01
如何更好地制备玻璃?
我们通常希望制备更好的玻璃,这里的“更好”可以指更硬,更能抵抗冲击,耐高温或其他一些性质。玻璃科学家有两种方法来优化玻璃的性能。
第一种方法是改变组分。与晶体相比,对于玻璃的组分调控是相当灵活的。探索不同的玻璃组分是金属玻璃研究领域的一个重要课题。(参见论文Jan Schroers, Physics Today, February 2013, page 32)
第二种方法是控制玻璃形成的制备路线。即使对于同样的组分,玻璃吹制工人也可以通过改变其形成过程来制备出明显不同的玻璃(如图1所示得到玻璃态的三种不同方案)。玻璃态的非平衡本质直接导致了玻璃性质对于制备过程的敏感性。以烹饪作为类比:即使使用相同的食材,不同的厨师也会做出不同口味的菜肴。
钢化玻璃的制作是利用了玻璃表面比内部更快冷却的原理。由于其形成过程中产生的内应力,钢化玻璃在破碎时会炸裂形成很多小碎片,而具有相同组分的、从液态缓慢降温得到的玻璃则会碎成一些较大的危险碎片。因此,制备过程可能会以一种惊人的方式影响玻璃的力学性能。智能手机的玻璃表面在组分和加工方面都进行了优化,从而稳健地保护着显示屏。
假设我们想要制作更高密度的玻璃,并期望它也能表现出更好的刚度 (stiffness) 和热稳定性。图1提供了一种方法:如果长时间维持在 以下,玻璃的体积将减少到过冷液体的体积,这一过程被称为物理老化 (physical aging)。这种致密化是驱使物质达到过冷液态的热力学驱动力的结果。然而,由于局部结构的重排需要极长的时间,这一致密化过程在动力学上受阻。这一情况实际上更糟,这是因为每向过冷液体迈进一步,就会形成一个新的结构,而这个结构发生重排所面临的障碍会更高。因此,通过物理老化实现的致密化过程随着时间呈对数减缓[4]。
另外,研究人员最近发现,高密度玻璃可以通过物理气相沉积方法 (physical vapor deposition) 进行更快地组装[5],如图2所示。玻璃自由表面的流动性可以比内部快 倍,这是形成高密度玻璃的关键。即使低于 ,表面附近的分子会快速向着过冷液态平衡,而这个过程在内部则慢得多。就像“堆砖块”电子游戏一样,进一步的沉积将把粒子堆积在合适位置上。
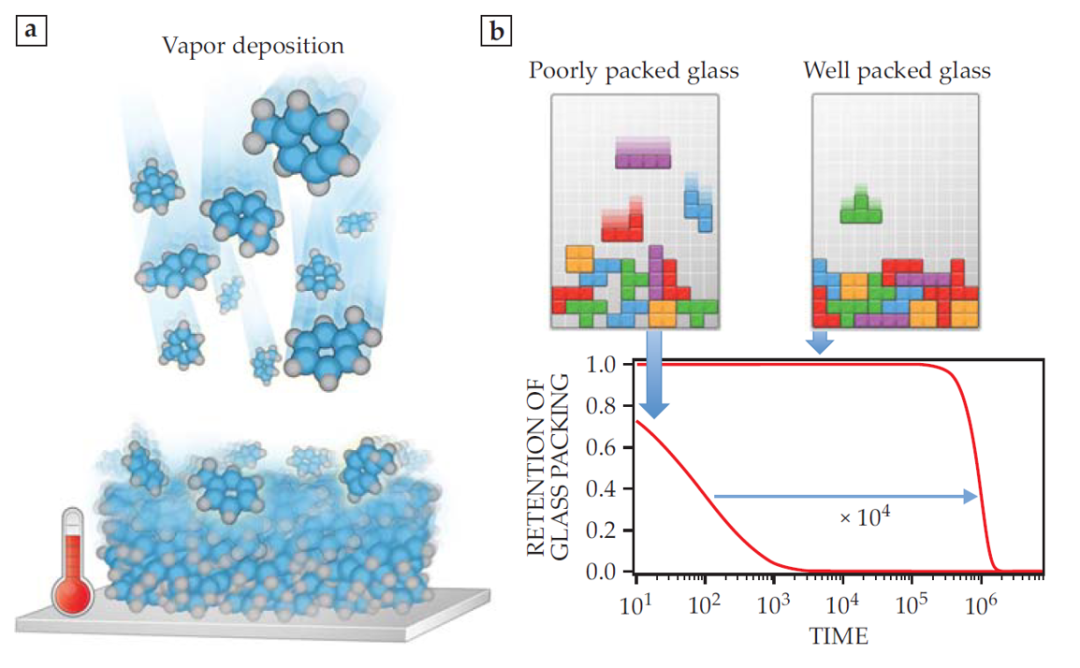
图2: 使用自由表面制备更好的玻璃。(a) 由气相沉积方法制备的玻璃表现出高效堆积,其中自由表面附近的分子运动是玻璃良好堆积的关键。如果选择正确的衬底温度,新来的分子会迅速平衡。(b) 通过堆砖块视频游戏,我们展示了更缓慢的沉积速率如何帮助玻璃更好堆积。当玻璃被再次加热到高于玻璃化转变温度时,分子的重排会破坏玻璃的原有堆积。以玻璃堆积的维持性为无量纲量(1表示完全维持,0表示完全损失),可以给出良好堆积的气相沉积玻璃。它相比不良堆积的玻璃能保持更久的玻璃态。这里的时间是以任意单位给出的。
表面快速流动与缓慢沉积方法相结合,可以使良好堆积的玻璃即使在高于 温度时也能表现出较高的动力学稳定性。利用物理气相沉积方法制备的超稳定玻璃比传统玻璃的密度高了近 ,而通过物理老化达到这样的密度则至少需要 年的时间。
利用物理气相沉积方法,可以制备出具有优异性能的高密度玻璃。相较于通过液态降温得到的玻璃,这些玻璃具有更低的焓。这个结果提供了第一手资料,展示了如果液态可以延伸到低于 的温度,过冷液体可能会表现出什么样的行为。通过气相沉积得到的玻璃具有更高的刚度,进行了非常有效的堆积,在被加热到 以上时,它们可以通过一个尖锐的转变锋转变为液体——这种行为更像是晶体的等温熔化,而对于从液态降温得到的玻璃,观察到的则是逐渐软化(softening)。
高密度玻璃高效堆积的另一个标志是,它们的热容最近被证明与温度呈立方依赖关系,直到低至0.6 K[6]。在这方面,高密度玻璃类似于非金属晶体,声子是热容的主要贡献者。相比之下,从液态降温得到的低密度玻璃的热容在低温下随温度大致是线性依赖,这种行为被认为是非晶固体中普遍存在低温激发的证据。
制备高密度玻璃的沉积方法也可以用来产生取向玻璃 (oriented glass),即分子在薄膜中具有面取向。用于手机显示屏的有机发光二极管就是由气相沉积法生产的玻璃制成的。在这些玻璃薄膜中,发光分子的平面取向的形成可以使显示效率提高30 以上。
02
物质的真实状态
在实际过程中,通常是从液态出发,使用有限降温速率制备玻璃,这种玻璃相对于过冷液体处于热力学非平衡态。但是,如果我们使用无限缓慢的降温速率进行冷却而不发生结晶,玻璃又将会处于什么状态呢?是否存在液体到玻璃的平衡相变呢?这些问题涉及到包含无序、杂质和多体相互作用的复杂系统的相变统计力学的基本问题。虽然几十年来进行了大量的研究,并取得了一些进展,但这些问题仍没有得到令人满意的答案[2, 3]。
在传统的朗道相变方法中,我们在基于对称性推导出自由能的表达式之前,必须首先选择一个序参量,例如,铁磁相变中的磁化强度,液气相变中的密度。对于一阶相变,序参量从非零到零的转变是非连续的,而对于二阶相变,序参量则遵循代数上的标度律,在临界点附近序参量的变化是连续的。
对于假定的从液体到玻璃的相变,并不容易选择出序参量。这是因为玻璃中的分子排列与液体中的非常相似(见图1),两态之间没有明显的对称性破缺。相反,两态在动力学上有所区别:液体可以自由地探索许多不同的无序构型,而玻璃则不能。
最近,通过平均场极限下的研究,玻璃化转变的问题得到了解决。该方法类似于研究铁磁的Curie-Weiss方法或研究液气相变的范德瓦尔斯理论,后两种方法都忽略了涨落。更具体地说,对于硬球粒子相互作用的平衡相图,其精确解可以在无穷维下在数学上被严格导出,此时的平均场近似是精确的[7]。在这种极限下,我们可以明确液态与玻璃态之间平衡相变的存在,并全面地研究相变的性质。由此产生的玻璃化转变的范德瓦尔斯图像深深地植根于至少25年前无序材料相变的理论发展[8]。
在液气相变的平均场理论中,自由能的两个极小值对应于液态和气态,我们可以选择密度作为序参量来区分这两个态。但对于玻璃化转变,由于玻璃态的结构和液态的过于接近,无法用同样的方法进行处理。因此,玻璃物理学家构造了新的物理量,称为重叠函数Q(overlap function),以区分玻璃态和液态。该函数描述了在同一温度下,统计独立平衡态构型间分子位置的相似度。当Q=0时,两构型不存在相似性,而当Q=1时,可以认为两构型相同。之后,我们就可以在平均场极限下用平均重叠函数表示自由能V(Q)[8]。如图3所示,自由能再次出现两个极小值。Q=0的极小值对应于液体,Q接近1时的极小值则对应于玻璃态。
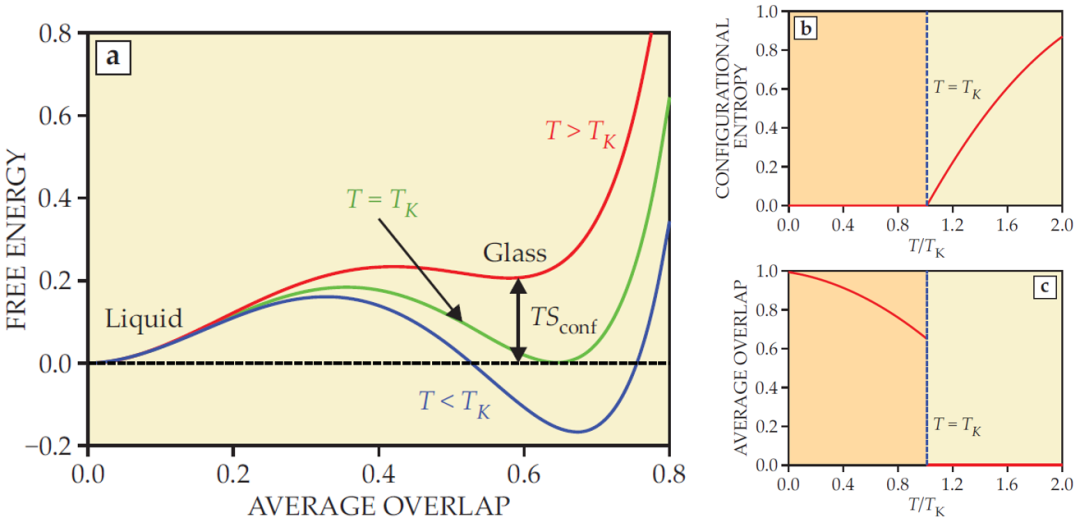
图 3: 平衡液体-玻璃相变的平均场理论。(a) 液-玻璃的平衡自由能的表示方式类似于液-气相变,但横轴上使用的是平均重叠度(该量可以量化一对构型的相似性)而非密度。对于Kauzmann转变温度( )以上,液体(平均重叠度为零)是稳态相。构型熵 表示处于亚稳玻璃相(平均重叠度非零)的自由能成本。(b) 当温度朝着 降低时, 快速减小并在 处为零。(c)在 处,系统非连续地跃变为具有高平均重叠度的玻璃相。在 以下,重叠度较大,构型熵为零。这里的有量纲量均是以任意单位给出的。
如果从高温液态随机选取一对构型,此时可用构型的数量非常多,以至于两者之间的粒子位置几乎是非常不同的,此时Q=0的极小值主导着自由能景观;与之相反,低温玻璃的两个独立构型几乎是相同的(但仍然无序),它们的相互重叠度Q很大。具有相同自由能极小值的两个构型所处的温度被称为Kauzmann温度, 。在平均场理论中,理想的玻璃化转变表现为Q在 处的非连续变化,高温下为低重叠相,低温下为高重叠相。基于这个原因,它被称为随机一阶相变[8]。
在Tk以上,如果系统占据势能景观的受限区域,就必须付出自由能成本。液体稳态和玻璃亚稳态之间的自由能之差量化了该成本。阻止系统探索不同状态会导致熵损失,这被称为构型熵 。在平均场理论中,随着温度的降低接近 , 会消失,并在玻璃相中维持为零,如图3所示。
理想玻璃化转变与Sconf消失相关,这个概念可以追溯到近70年前的沃尔特·考兹曼 (Walter Kauzmann)、杰拉尔德·亚当 (Gerold Adam) 和朱利安·吉布斯 (Julian Gibbs) [9]。最近,根据(气相沉积方法得到的)超稳定玻璃的结果,可能有办法在实际材料中直接探测具有低 的过冷液体。此外,研究人员正在开发新的计算技术,以探索实验温度区间的玻璃态,并对有限维平均场理论的有效性提供更直接的见解[10]。
对于高于Tg的液态,热力学图像和缓慢分子运动之间的联系更为复杂,因此更具争议。然而,与一阶相变的类比暗示了一种解释分子重排动力学的物理机制。
在图3中,Tk以上的Sconf代表了从局部亚稳玻璃态弛豫到液相的热力学驱动力。由经典成核理论启发的标度论证,提供了弛豫的时间尺度,它以1/( )为指数呈指数形式,其中 表示玻尔兹曼常数。降温接近 时,弛豫时间发散, 为零,而在低于 时,玻璃相的弛豫时间均为无穷。对该现象的物理解释是,随着温度的降低,动力学减缓,可用构型越来越少,而构型之间的动力学路径越来越复杂并表现出集体动力学。
根据以往在相变物理方面的研究经验,当考虑有限维涨落时,与平均场极限有关的想法可能会完全失效。虽然在简单相变的现代理论描述中已成功地包含这种涨落,但人们仍在对有限维涨落进行深入研究,以解决无序和复杂自由能景观所带来的问题。
与此同时,研究人员正在探索平均场方法的理论替代方案。例如,一种基于实空间动力学激励 (real-space dynamic excitations) 的方法,通过空间关联分子位移的稀疏集合的涌现来描述液体弛豫动力学[11];另一种方法则考虑了局部有利的几何图案 (geometrical motifs),并将整体无序的液体结构视为拓扑上不同团簇的组装[12]。
03
玻璃包含缺陷吗?
缺陷是有序凝聚态物理学的核心。物理学家通常将晶体的形变和断裂视为缺陷动力学。例如,当原子的一个平面滑过另一个平面时,晶体金属就会形变。然而,考虑到玻璃材料自身的无序性,在玻璃中显然不可能出现类似的滑移面。
如果把晶体缺陷的概念套用到玻璃上,那么关于玻璃缺陷的整个想法可能会被驳回。因为玻璃中与堆积有关的一切看起来都是有缺陷的,而缺陷只有在它们稀疏的时候才是有用的考虑对象。然而,最近的研究发现,稀疏缺陷 (sparse defects) 或柔性区域 (soft spots) 似乎起着重要的作用,这一发现令人惊讶。
当玻璃在低温下形变时,人们观察到空间上的局部不可逆重排,通常被称为剪切转变区(shear transformation zones),即使在低应变下也是如此[13]。剪切转变区充当着缺陷的作用,但又仅在发生力学形变时才表现出来。与晶体中的缺陷不同,玻璃中的这些缺陷与明显的结构特征无关,因此很难预测玻璃将从哪里开始流动。在计算机模拟或用显微镜追踪胶体粒子的实验中,剪切转变区仅在发生该事件之后才能很容易地被找到。
目前的观点是,当玻璃发生形变时,应变首先在少数剪切转变区域局部发生,随着形变的进一步发展,这些区域会在空间上相互组织在一起形成剪切带 (shear bands) ,这些剪切带代表了材料形变集中的平面。这种集中最终会导致玻璃在大尺度上破裂。
由于剪切转变区提供了玻璃断裂的分子观点,因此理解这些区域的结构起源并预测其行为就成为了研究重点。根据最近的计算机模拟结果,研究人员已经假设玻璃中的剪切转变区与局部低频振动相关[14]。
在晶体中,低频振动模式涉及到大量原子。尽管玻璃中的一些低频模式也具有这种特点,但还有一些低频模式涉及到的原子数异常少,而这种模式在完美晶体中是不存在的。因此,似乎是这些局部低频模式与剪切转变区相关。人们可能将剪切转变区视为玻璃的不利堆积区域,但目前还没有结构测量方法可以直接识别。
当温度升高时,热涨落自发地引起越来越多的分子进行重排。实验和模拟结果表明,在略高于 时,分子运动出现空间异质性 (heterogeneous),在时间上是高度间歇的。换句话说,玻璃中一些区域的分子可以运动,另一些区域内的则不能,还有一些区域可以处于运动和不运动的交替状态。这样的动力学异质性[15]意味着在 附近的热力学活化流具有高度集体性,其特征是动力学关联长度随着温度的降低而适度增加。如果在玻璃流动期间观察到运动区域和剪切转变区域之间存在联系,将会是很有吸引力的,并且,阐明这种联系也是当前研究的一个主题。
04
其他科学领域中的玻璃物理

图 4: 不同长度尺度下的玻璃物理学。原子液体和由更大粒子构成的体系具有很多相似之处。(a) 高浓度的胶体微米尺寸小球类似于图 1 中展示的液态和玻璃态。(b) 挤压在两个平板之间的由活细胞组成的稠密粘性液滴表现出很多玻璃的性质。(c) 密集的蚁群可以长时间保持其形状,类似于无定形固体。
玻璃性和无序结构阻滞态的物理性质与许多具有不同长度和时间尺度的材料有关。图4给出了软凝聚态物理和生物中的一些例子。软材料通常是一些超分子的致密聚集体。以尺寸介于20纳米到1微米的胶体粒子制成的玻璃充当了研究玻璃化转变的简化模型体系。胶体粒子充当了“大号原子”,它们的尺寸大到可以在显微镜下进行观察,但又小到可以悬浮在溶液环境中并表现出明显的布朗运动。胶体玻璃实验在采用简化模型的计算机模拟与原子、分子玻璃的实验研究之间建立了重要联系[16]。
由于可以通过各种物理方法来调控胶体相互作用,因此胶体玻璃可以通过多种微观相互作用形成。例如,具有极短程相互作用的胶体粒子表现为粘性球体,并提供了胶体世界中独特的模型系统。这些新型软玻璃材料的振动及力学性质与原子或分子玻璃有着定性的区别,后者具有比粒子尺寸还大的长程相互作用[16]。
带有粘性区域 (sticky patches) 的胶体粒子可以被用来精细控制其结合角度,这是合成各种玻璃的胶体类似物的第一步。这些类似物中包括二氧化硅(窗户玻璃的主要成分)和玻璃化的水,它们的性质目前仍处在争论当中。这种新型胶体材料可用于在粒子尺度上可视化和理解其分子对应物的物理性质。
研究人员也越来越关注活性物质框架下的玻璃化转变,例如自推进胶体粒子。这些研究与生物系统有很好的联系,比如密集的细菌菌落和有着集体动力学的上皮组织细胞[17]。在许多生物系统中,粒子的密度可能很大,因此微观动力学可以变得缓慢并类似于玻璃状态。
为了解决与致密组织的力学性质或与细胞内拥挤环境中的蛋白质扩散相关的问题,我们对玻璃物理学的理解正在扩展。除了热涨落之外,化学和力学驱动力也被考虑在内。人群和动物聚居地,动力学抑制也经常发生:当密度过大时,流动几乎停止,就像在高峰时间挤在地铁里一样难以移动。
玻璃化转变也出现在计算机科学更为抽象的问题中[18],例如在给定约束条件下回答一组问题的优化算法。当约束条件增多时,想要满足所有约束条件就变得愈发困难,计算机可能会陷入到大量良好但不完美的答案中。以坚硬且不重叠的物体堆积为例,当体系的堆积比例较高时,任何两个物体都不重叠的约束条件就变得如此苛刻,以至于无法在高于次优堆积比例时找到可能的解决方案。这种情况类似于玻璃化转变。
如果一个问题不能通过一系列的步骤来解决(这些步骤是输入一定数量的多项式函数),那么这个问题就被认为是计算困难的。对于某些类型的计算难题,用于处理玻璃统计力学的方法已经表明,当约束数量增加时,解的数量会减少,这与图3中所示的液体到玻璃的转变直接相关。这些方法甚至导致了物理学启发的计算算法的发展,用于解决计算机科学中的难题。这些算法之所以成功,正是因为它们是基于解决玻璃科学家所面临的复杂自由能景观的方法[18]。这些方法现在在图像压缩和纠错码等领域得到了应用。
玻璃物理内容丰富且应用广泛。正如上文所述, 玻璃科学的基本思想正深刻影响着软凝聚态物理、生物物理以及计算机科学等多个领域。在许多现代技术中,玻璃状材料作为其中的重要组成部分。随着新用途不断的发掘,研究人员在实验和理论两方面正在向前阔步,以期对玻璃态有一个满意的基本理解。
参考文献
[1] J. Zhao, S. L. Simon, G. B. McKenna, Nat. Commun. 4, 1783 (2013).
[2] M. D. Ediger, C. A. Angell, S. R. Nagel, J. Phys. Chem. 100, 13200 (1996).
[3] L. Berthier, G. Biroli, Rev. Mod. Phys. 83, 587 (2011).
[4] C. A. Angell et al., J. Appl. Phys. 88, 3113 (2000).
[5] S. F. Swallen et al., Science 315, 353 (2007).
[6] T. Pérez-Castañeda et al., Proc. Natl. Acad. Sci. USA 111, 11275 (2014).
[7] P. Charbonneau et al., Nat. Commun. 5, 3725 (2014).
[8] T. R. Kirkpatrick, D. Thirumalai, P. G. Wolynes, Phys. Rev. A 40, 1045 (1989); S. Franz, G. Parisi,
Phys. Rev. Lett. 79, 2486 (1997).
[9] W. Kauzmann, Chem. Rev. 43, 219 (1948); G. Adam, J. H. Gibbs, J. Chem. Phys. 43, 139 (1965).
[10] G. Biroli et al., Nat. Phys. 4, 771 (2008); W. Kob, L. Berthier, Phys. Rev. Lett. 110, 245702 (2013).
[11] D. Chandler, J. P. Garrahan, Annu. Rev. Phys. Chem. 61, 191 (2010).
[12] G. Tarjus et al., J. Phys. Condens. Matter 17, R1143 (2005).
[13] A. S. Argon, Acta Metall. 27, 47 (1979); M. L. Falk, J. S. Langer, Phys. Rev. E 57, 7192 (1998).
[14] A. Widmer-Cooper et al., Nat. Phys. 4, 711 (2008); M. L. Manning, A. J. Liu, Phys. Rev. Lett. 107,
108302 (2011).
[15] L. Berthier, Physics 4, 42 (2011).
[16] G. L. Hunter, E. R. Weeks, Rep. Prog. Phys. 75, 066501 (2012).
[17] T. Vicsek, A. Zafeiris, Phys. Rep. 517, 71 (2012).
[18] M. Mézard, A. Montanari, Information, Physics, and Computation, Oxford U. Press (2009).
感谢原文作者,法国蒙彼利埃大学的 Berthier 教授和美国威斯康星大学麦迪逊分校的 Ediger 教授,对于本文翻译的支持。
本文经授权转载自微信公众号“中国科学院理论物理研究所”,征得作者同意,译自科普文章 Berthier L, Ediger M D. Facets of glass physics[J]. Physics Today, 2016, 69(1)原题目为《Doctor Curious 48: 玻璃物理的诸多方面》。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 