
导读
几个世纪以来,计算机(机器)一直是数学家的好朋友,他们利用它计算、提出猜想以及进行数学证明。随着交互式定理证明器、机器学习算法和生成式AI等更为先进的工具的出现,机器被更具创新性和深度的方式得到运用。
近日,在MSRI(美国数学科学研究所,现改名SLMath)四十周年庆典上,陶哲轩(Terence Tao)对机器辅助数学证明的历史和最新发展进行概述,并对数学中的机器辅助将扮演的未来角色进行预测。
他表示:早期的计算机辅助的数学研究以女性为主,并衍生出了一个计算能力单位:“千女时”,一千个使用加法器的女性能完成多少计算。“千女时”的出现也标志着大规模计算的起源。
而现在的计算机已经超越了“暴力穷举”,它逐渐能够提供创造性的建议,帮助人们在数学研究中找到新的方向和灵感。尤其是GPT-4:“与这些先进的语言模型进行对话,能以间接的方式激发其数学思维,它就像一个非常耐心的同事,善于倾听而不评判。”
对于未来计算机在数学中作用,陶哲轩说道:“人类与计算机在数学创造领域的贡献比是95%和5%,那么再过十年或者二十年,这个比例就会变成五五开”。
推荐理由:希望以此为契机,呼吁研究者关注AI在辅助数学证明方面发挥的惊人作用,机器学习提供了强大的框架,为数学家开辟了新思路。未来,AI有巨大的潜能帮助解决那些对人类来说极具挑战性的数学难题,模拟和执行高级数学运算,乃至提出新的数学猜想和理论。以下为演讲全文,编辑做了不改变原意的编译,请欣赏:

视频地址:
曾有人询问我美国数学科学研究所(MSRI)以及数学的发展方向时,我认为计算机在数学领域的应用和作用将会变得越来越重要。
计算机已经在数学交流中发挥出重要的作用,例如用LaTeX进行写作,用电子邮件、视频会议与合作者进行沟通。在纯数学方面,计算机的作用还没受到重视,但情况正在改变。
过去,人类与计算机在数学创造领域的贡献比是95%和5%,那么再过十年或者二十年,这个比例就会变成五五开。要达到5(人):95(计算机),可能还需要花费很长的时间。
早期的机器与数学:人工的、机械的,女性主导的

早期计算机的关键词是人工、机械,在18和19世纪,计算机的主要作用是进行数字计算、建立对数表和三角函数表。
在20世纪20年代,物理学家亨德里克·洛伦兹利用人工计算机团队来模拟大坝(阿夫斯吕伊特戴克)周围的水流。这是一个重要的工程项目,需要进行大量复杂的计算,洛伦兹和他的团队采用了浮点运算,这是一种在当时并不常见的计算方法。
在战争前计算机已经可以部分求解偏微分方程了。在第一次世界大战和第二次世界大战中,计算机帮助人类在弹道学、导航、曼哈顿计划等方面进行了大量的数学计算。实际上,大部分工作是由人工计算机完成的,这些人工计算机主要由女性操作。因为当时的男性正在参战。这也衍生出了一个计算能力单位:“千女时”,一千个使用加法器的女性能完成多少计算。“千女时”的出现也标志着大规模计算的起源。
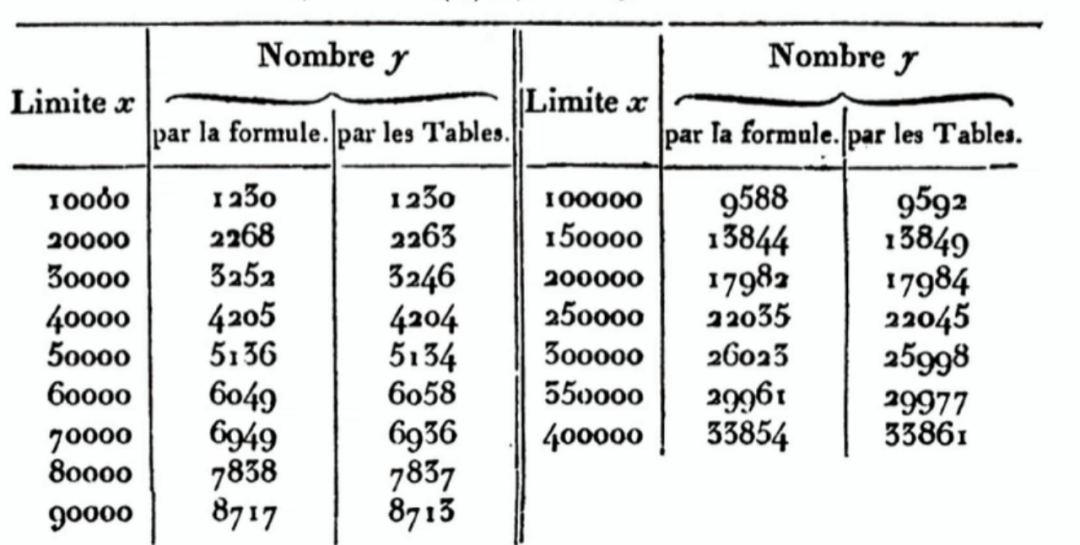
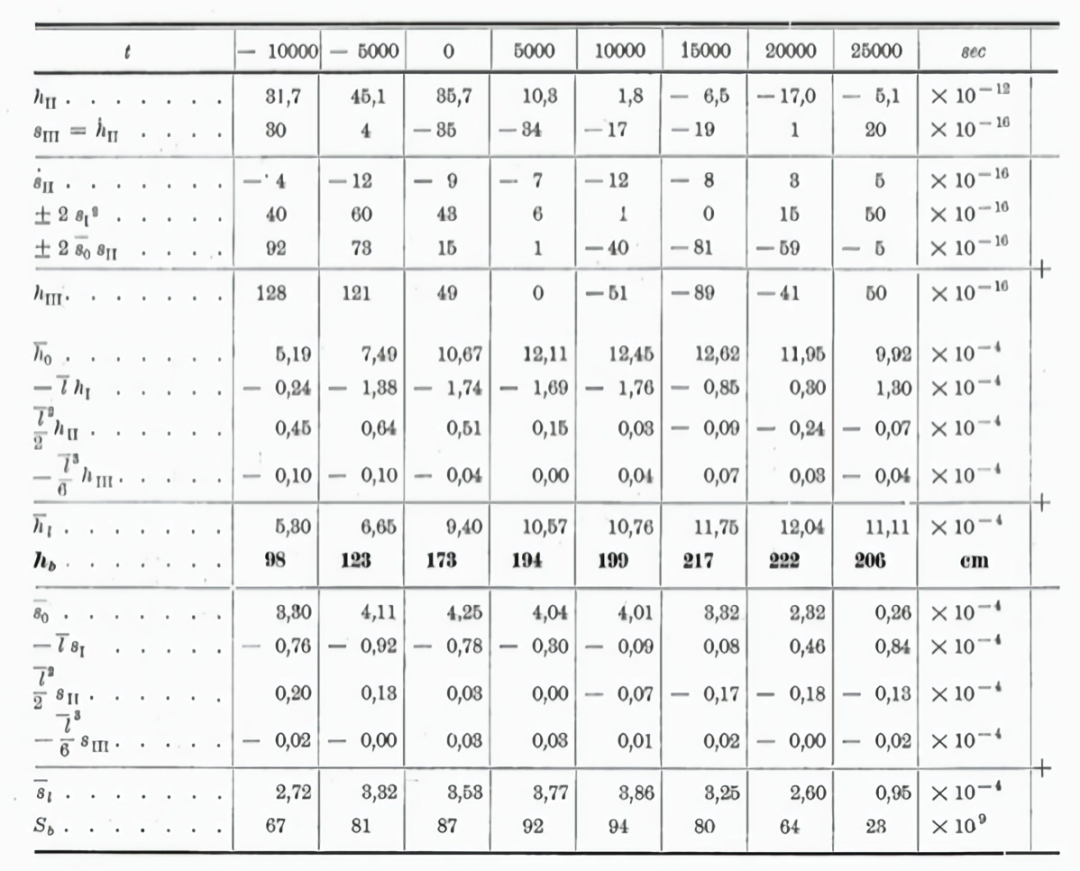
图注:高斯和勒让德利用了素数表(达到大约10^6)来研究一个基本问题:在给定阈值x之前有多少个素数(记作π(x))
研究型数学家是如何使用计算机的呢?除了建立表格等之外,最早的用途之一就是做出猜想。18世纪高斯和勒让德(Gauss and Legendre)在研究素数时利用大规模人工计算机构建了大量素数的表格,用于“猜想”素数分布的规律。
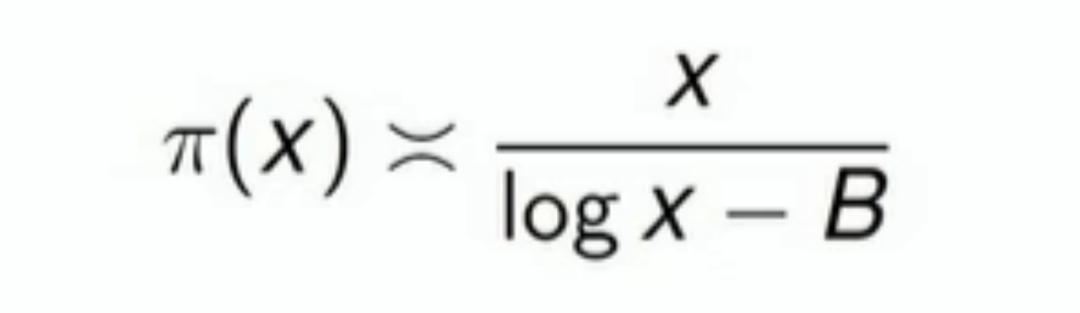
图注:勒让德的素数分布猜想公式
尽管勒让德的素数分布猜想在精确性上存在一些问题,但它的影响力仍然非常大。后来,这个猜想被狄利克雷修正为一个更准确的形式,这个形式现在已经被广泛接受并被纳入教科书。
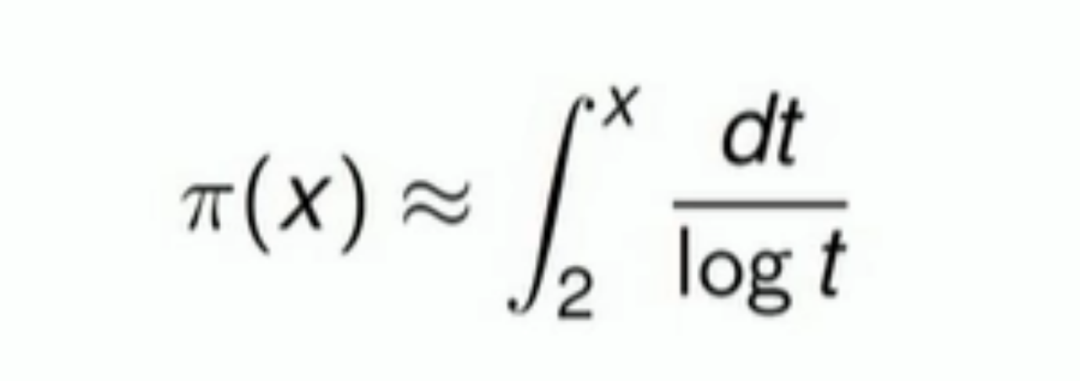
图注:狄利克雷修正后的公式
计算机加持下的数值计算现在已经成为解析数论中的常规工具,被用来帮助形成和验证猜想。伯奇和斯温内顿-戴尔猜想就是一个很好的例子,这个未解的数学问题是通过大量的数值计算和数据分析来提出的。
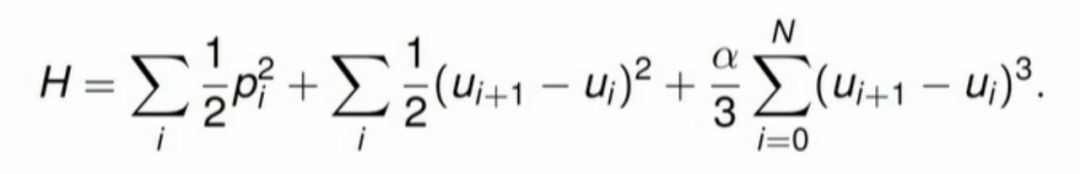
图注:能量均分定理表达式
电子计算机时代:点开多项数学辅助技能树
在二战后,物理学家恩里科·费米(Enrico Fermi)、约翰·帕斯塔(John Pasta)、斯坦尼斯洛·乌拉姆(Stanislaw Ulam)和程序员玛丽·青果(Mary Tsingou)为了给电子计算机“MANIAC”找到新的应用,决定模拟晶体的演变。他们将晶体视为一串一维粒子,这些粒子通过哈密顿方程进行演变。按照能量均分定理,所有的能量应该匀地分散在所有模式(即晶体中的各个粒子)中。
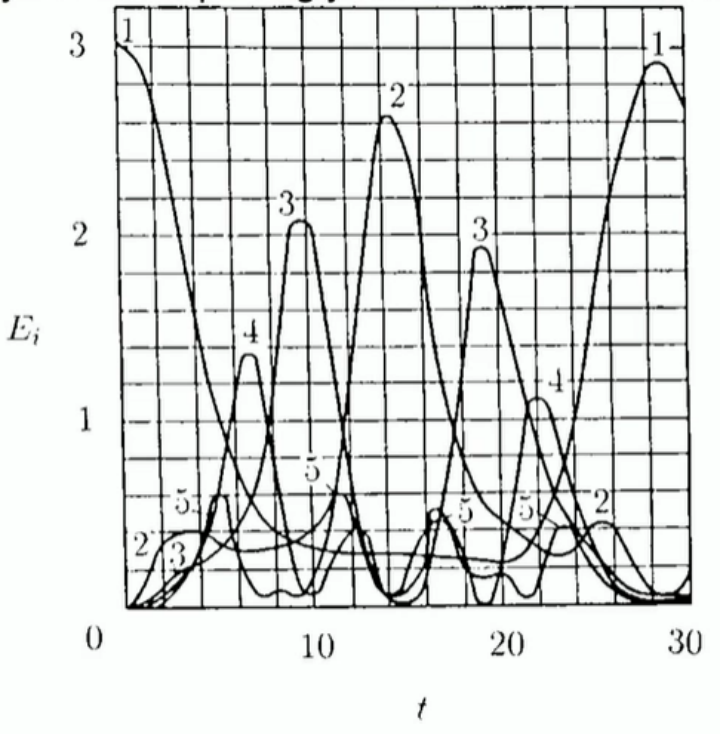
图注:实验结果表示能量并不均分,找到的是稳定局部解(孤波)
但实际运行数值模拟时,结果并未符合他们预期的能量均分定理。起初,他们设定了一个初始状态,其中只有一个粒子的能量被激发。然而,随着时间的推移,能量并没有均匀分布,而是出现了在某一两个粒子之间的长期稳定。也就是就是出现了孤波(或叫孤子)的现象。
然而,用计算机进行长时间运行实验,现象会消失,能量最终会均匀分布。
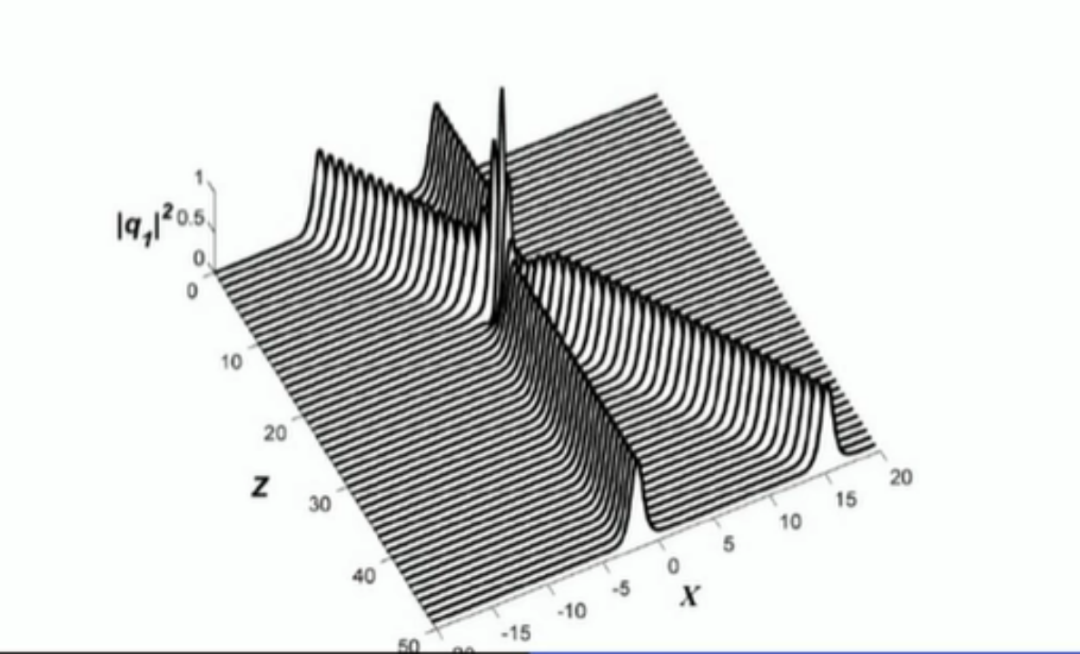
这种现象的出现是因为他们研究的系统其实是一个完全可积系统——投达晶格方程(Toda lattice equations)亦称投达链——的近似。在这个完全可积系统中,孤子是会永久存在的。而他们实际的系统并不是完全可积的,但却足够接近,以至于他们能在模拟实验中看到孤子现象。
这个具有巨大影响力的数值实验开启了可积系统的研究,也开启了孤波的稳定性研究,这个研究领域至今仍然活跃。

图注:阿佩尔和沃夫冈·哈肯在1976年用计算机辅助证明了四色定理。
在现代电子计算机的初期,计算机的威力在于它们能够揭示出一些“意料”之外的现象。四色定理可能是大家最熟知的一个通过计算机得证的定理。在其证明中,凯尼斯·阿佩尔(Kenneth Appel)和沃夫冈·哈肯(Wolfgang Haken)编写了一些特定的程序,这些程序可以处理特定的图,并通过计算机检查这些图的某些性质。如果某一特定的图能够满足这些性质,那么就能用四种颜色来对其进行着色。这就是通过计算机得以证明的四色定理。
四色定理的证明分为两个主要部分:可归化和不可避免性。可归化部分表明,任何包含1834种配置中的任何一种的图都可以转换为更小的图,且如果更小的图可以四色着色,那么原图也可以。这部分证明是通过将这些配置逐个输入计算机完成的。
不可避免性部分表明,如果存在一个不能四色着色的图,那么它必须包含1834种配置中的至少一种,这部分通过手动检查超过400页的微缩胶片来验证。
从现在的标准来看,Appel-Haken的原始证明含有一些可修复的错误,并不符合现代的计算机可验证证明的标准。1996年,罗伯逊(Robertson)、桑德斯(Sanders)、西蒙(Seymour)和托马斯(Thomas)首次提出了一个真正的计算机可验证的证明,他们使用633种配置,这些配置的可归化和不可避免性都可由计算机检查。然后在2005年,维尔纳(Werner)和贡蒂埃(Gonthier)使用辅助工具Coq完全形式化了这个证明,使其成为一个真正的计算机可验证的证明。
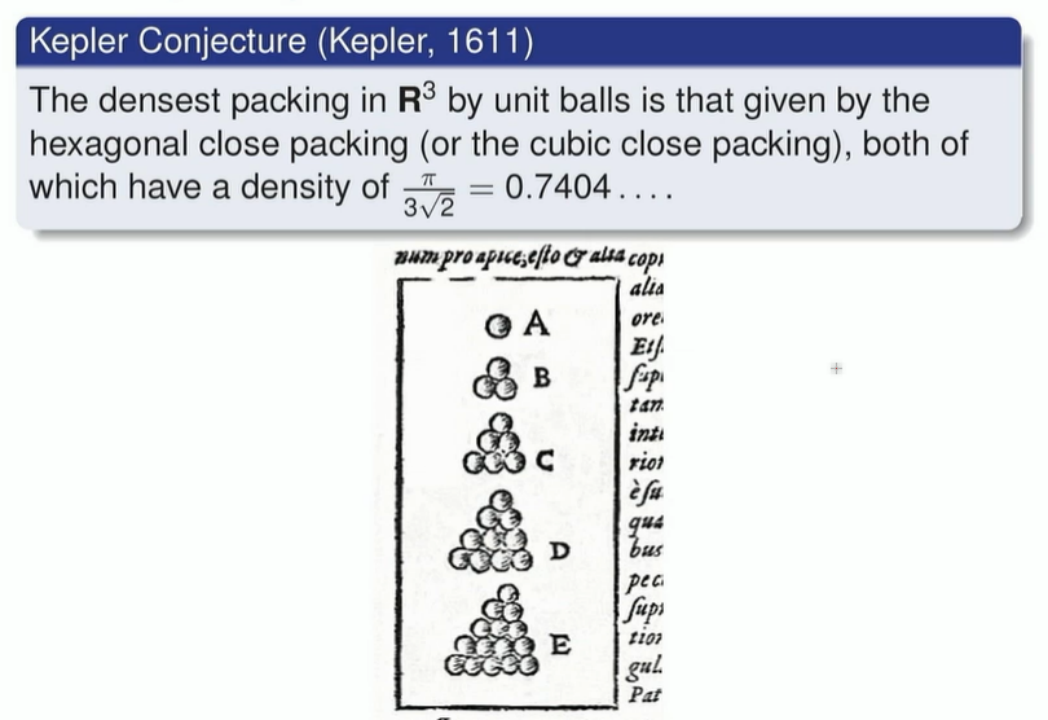
开普勒猜想是另一个计算机辅助数学证明的例子。在17世纪,开普勒研究了三维空间中单位球体的最密集堆积方式,发现两种堆积方式,即六方紧密堆积和立方紧密堆积,它们的密度都约为74%。开普勒猜测这是堆积密度的最大可能值,没有其他堆积方式可以超过这个密度。这个猜想至今仍是一个重要的数学问题。
开普勒猜想本质上是一个涉及无穷多变量的优化问题,这使得它并不容易通过计算机验证。尽管在1951年,Toth提出了一种可能的解决方法,即通过有限多个沃罗诺伊单元的体积上的某些加权不等式来寻找球体堆积密度的上界,但是,尽管经过多次尝试,但并没有找到能得出精确结果的有说服力的证明。
托马斯·海尔斯(Thomas Hales)和塞缪尔·弗格森(Samuel Ferguson)采取了一种灵活求解最小化问题的策略:调整评分函数,但这反过来又会产生更多的问题。然而,尽管评分函数变得越来越复杂,但他们的任务在某种程度上却变简单了。数篇论文发表后,两位学者终在1998年成功证明了开普勒猜想,证明方式是用线性规划设计出了一个复杂的评分函数。
据说,海尔斯最初并不打算使用计算机来帮助他证明这个猜想,但随着项目变得越来越复杂,他发现他必须要依赖计算机。最后他们的证明包含了250页的数学笔记,以及3GB的计算机代码、数据和结果。

为“打消”对开普勒猜想证明的疑虑,托马斯·海尔斯在2003年启动“Flyspeck”项目。他们使用证明助手的语言(the language of a proof assistant)来形式化证明过程,使得计算机能够自动进行验证。虽然最初估计项目需要二十年,但通过海尔斯和他的21位合作者的共同努力,项目在2014年完成。
近年来,彼得·舒尔茨(Peter Scholze)的液态张量实验无疑是最为人所知的形式化证明实验项目,涉及舒尔茨的"凝聚态数学"理论(condensed mathematics),目标是修复拓扑空间类别的一些问题,如拓扑阿贝尔群,方式是使用“凝聚”的新的数学对象来替代传统的拓扑空间类别。
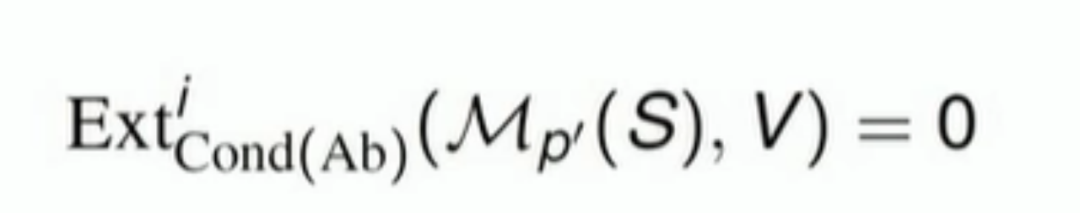
“凝聚数学”理论中的一个关键结果是“消失定理”, 研究发现,在特定的数学结构中,某些元素或属性在一定条件下会“消失”。消失定理是凝聚数学中的核心,它是使用凝聚数学进行泛函分析研究的基础。证明这个定理非常困难,舒尔茨花了一年研究,但进展缓慢。
于是,舒尔茨发起“液态张量实验”,希望用数学软件Lean对结果进行形式化,实现过程中,他们将几个基础的数学理论添加到了Lean的mathlib库中。最后,在舒尔茨和其团队的努力下,2021年5月,形式化了一个关键的子定理,2022年7月得到了完整定理的形式化。该项目的主要成就在于大幅扩充了Lean的数学库。事实上,由于该项目构建的丰富库例程,其他的Lean形式化项目变得更加便捷和高效。

图注:液态张量实验蓝图
形式化的过程同时伴随着一个人类可读的证明“蓝图”创建。这个"蓝图"以一种交互式的方式合成了正式和非正式的证明,这让舒尔茨和其他人能够更深入地理解这个证明。

图注:利用Lean证明拓扑定理。陶哲轩设想,未来的拓扑学教科书可能会使用这种交互式的步骤来解释证明,使学习过程更为清晰和简单。
受到这项工作的启发,越来越多的研究者正在开发软件工具,希望能够自动将形式化的证明转化为人类可读的交互式证明。
计算机作为辅助工具,通常发挥的作用方式有两种:1.逐渐增加形式化证明的使用;2.使用计算机进行暴力计算。例如2013年Helfgott解决奇数哥德巴赫猜想所使用的方案就是暴力计算+巧妙的优化。
人工智能时代:神经网络与大模型走进数学
我特别喜欢的例子是2016年的拉姆齐定理。先来看“布尔型毕达哥拉斯三元组问题”,它的内容大致是这样的:如果你把1到7825这些数字分成两组(也就是用两种颜色进行标记),那么无论如何分组,你都能在其中一组找到至少一组毕达哥拉斯三元组(满足a² + b² = c²的三个数),并且这三个数是同一颜色(在同一组里)。
这实际上是一个计算量非常大的3-SAT问题(3-可满足性问题,NP完全问题的一个例子),解决他并不能应用标准的3-SAT求解器,需要对3-SAT求解器进行特殊的定制或修改。
最后,胡埃莱(Huele),库尔曼(Kullman)和马雷克(Marek)利用计算机解决了这个问题。他们使用了一种叫做"布尔满足性求解器"的工具,在Stampede超级计算机上运行了四年,最终找到了所有可能的分组方式,并证明了无论如何分组,总能在其中一组找到至少一个同色的毕达哥拉斯三元组。这个证明的数据量非常大,原始数据大小达到了200TB,但是可以通过压缩降低到68GB。
在流体方程中,有两个著名的未解问题:纳维-斯托克斯方程(Navier-Stokes equations)和欧拉方程(Euler equations)的有限时间爆炸。十年前,数值模拟给出了一些看似发展出奇异性的解:它们开始时是平滑的,但随着时间推移变得越来越湍流,能量开始集中在某些特定的点。但是,由于计算精度的限制,当模拟接近奇异性发生时,这些数值结果就变得不可靠。
学界认识到,如果可以找到一个特定的类型的解,即自相似解(self-similar solutions),那么就可能证明流体方程在有限时间内发展出奇异性。这类似于在广义相对论中寻找闭合的测地线(geodesic)或轨道。
使用计算机能找到一个“近似”的自相似解。这个解并不完美,但接近完美的自相似解,只有微小的误差。但如果能结合严格的稳定性分析,就可以证明实际自相似解的存在。这是理想化的方法,可视为“梦想”,在实际操作中可能很难实现。
在2022年,发展出了两种求自相似解的方法:1. 陈-侯方法,采用传统的数值偏微分方程,通过计算机辅助进行严格的稳定性分析,这是首次为不可压缩欧拉方程的光滑解在圆柱边界之外建立有限时间爆破结果的严格证明;2. 王-赖-戈麦斯-塞拉诺-巴克马斯特方法:使用了物理信息神经网络(PINN,Physics Informed Neural Network),这是一种结合物理学知识与神经网络的技术。
也有许多研究人员正在积极运用机器辅助技术来探寻流体方程的“爆破解”。但是,流体动力学中的一个非常复杂问题:纳维-斯托克斯方程的全局规律性,目前似乎仍然难以解决。

在纽结理论(knot theory)领域中,计算机和人类数学方法发生了有趣结合。扭结理论研究的是,将线缠绕在空间中形成的结的性质。学界目前努力在将纽结理论的双曲不变量(由实数和复数组成的集合)与结论的符号差(signature一个整数)联系起来,以更好地理解结的性质和结构。代表工作由亚历克斯·戴维斯(Alex Davies)等人的团队作出。
他们最近的进展是人工神经网络所带来的。他们使用神经网络,在包含超过两百万个“结”的数据库上训练。训练后的神经网络非常成功,能够准确预测从双曲不变量到签名的转换。这也表明双曲不变量和签名之间确实有联系。
然而,神经网络的工作方式就像一个“黑盒子”,可以看到它的输入和输出,但是里面究竟发生了什么,人们并不知道。因此,双曲不变量和签名之间的具体关系,目前也无法通过人工神经网络得知。
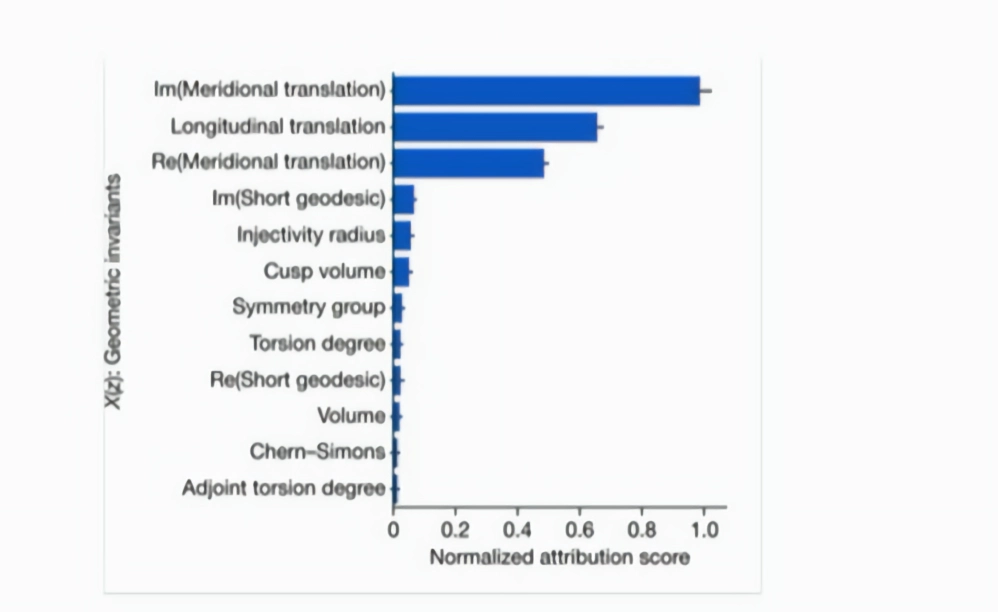
图注:用于预测签名的主要双曲不变量
于是,他们进行显著性性分析,来确定哪些双曲不变量对预测签名的关系最重要。换句话说,他们想知道改变哪些输入参数会对输出结果产生最大的影响。最终,他们发现24个双曲不变量中只有3个对预测签名的关系有显著影响。这意味着,尽管他们一开始可能以为所有的不变量都很重要,但实际上只有其中的一小部分真正关键。因此,神经网络+显著性分析有助于更深入地了解这双曲不变量和签名之间的关系。
使用类似于“整数序列在线百科全书(Online Encyclopedia of Integer Sequences)”的特殊数据库可以挖掘数学中不同领域间的隐秘联系。这样的联系可能表现为两个完全不同的领域产生相同的数字序列,就像数学中著名的“怪兽月光理论(Monstrous moonshine)”现象那样。
未来,希望有更多自动化工具能够在更深的层面上发现不同领域之间的联系,例如两篇来自不同领域的论文可能证明了相似的定理,那么这些工具能够清晰“识别”。尽管这样的“语义搜索”技术可能还需要至少一年的时间才能实现,但它展示了一种令人充满期待的未来趋势。

图注:GPT-4解决数学问题
大模型在数学研究过程中也表现出了一些潜力,例如GPT-4甚至可以解决2022年国际数学奥林匹克竞赛中的问题,展现了其在数学领域的应用能力。

图注:大模型最初给出的答案是120
但这个系统在处理数学问题时并不稳定。虽然它有时候出人意料,但同时也可能在解释或计算数学概念方面产生错误,甚至在处理基本算术问题时也会出错(如7*4+8*8=120的错误)。因此,当前的技术水平可以看做“困惑的本科生”,虽然已经记忆了所有内容却不真正理解。
有学者尝试通过一些新的方法来让那些大语言模型变得更懂数学,包括与Wolfram Alpha等传统计算工具结合以及融合传统数学解题策略。除此之外,与这些先进的语言模型进行对话也能以间接的方式激发其数学思维,它就像一个非常耐心的同事,善于倾听而不评判。大模型表现出的这一特点,也能促进人类探索新想法和创造性思考。
总结:鼓励尝试人工智能工具
那么,计算机辅助证明现在进展到什么地步了?首先明确它还似乎不太可能独立解决主要的数学问题;抛开前面那个奥林匹克问题不谈,如果你向ChatGPT简单输入“请为我解决黎曼猜想”,可能得到似是而非的胡言乱语。
其次它越来越多地被用于支持人类数学家的工作,与暴力穷举或计算不同,现在的计算机逐渐能够提供创造性的建议,帮助人们在数学研究中找到新的方向和灵感。
总结一下,人工智能技术,在短期内,可能在数学研究的辅助方面产生更多影响,例如自动总结大量文献或建议相关工作,但它还无法触及核心方面。我鼓励大家尝试人工智能工具,它与我们通常使用的挑剔工具(如LaTeX,一个括号可能导致全盘错误)不同,能够容忍非常模糊的输入,并从中得到结构化和有趣的答案。
本文经授权转载自微信公众号“智源社区”。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 