从1897年德国数学家戴德金给出了“戴德金数”的定义，数学家到2023年才找到了9个戴德金数。该数字长达42位，耗尽了现在最强的算力，我们何时才能找到第10个戴德金数？
撰文 | 张和持
戴德金数是一串增长非常迅速的数列，以德国数学家戴德金（Richard Dedekind，1831-1916）命名，最初于1897年给出定义。1991年，数学家找到了第8个戴德金数，数字长达23位。30多年后的2023年，数学家终于计算出了序列的第9个，其数字长达42位。对戴德金数的计算很大程度上反映了当今计算机的算力，因此何时能迎来第10个戴德金数仍未可知，似乎遥遥无期。
何谓戴德金数
在给出戴德金数的定义之前，我们先来看一看目前已经得到的计算结果。我们把第 个戴德金数计作 ，那么从 到 的十个戴德金数如下：
0 | 2 |
1 | 3 |
2 | 6 |
3 | 20 |
4 | 168 |
5 | 7581 |
6 | 7828354 |
7 | 2414682040998 |
8 | 56130437228687557907788 |
9 | 286386577668298411128469151667598498812366 |
戴德金数指的是 元单调布尔函数的个数。所谓 元布尔函数，就是 的函数，输入 个布尔变量，输出一个布尔变量。这其实是一个非常具体的概念，计算机底层的输入和输出都是二进制数据，所以这套理论不可避免地会与计算机科学扯上关系。当 的时候，为了方便起见，人们约定有两个布尔函数：常数函数 和 。这样约定有一个好处，我们可以将布尔函数认为是集合 的幂集 到 的映射
是的子集
时， 之间的一一对应关系可以这样理解：每个 元布尔变量都对应着一个 的子集 ，其第 个分量为 表示 这个数不在 中，而为 则表示 。例如， 时， 对应 。而 时， 只有一个元，要么 要么 ，所以有两个布尔函数。
给定 ，幂集里一共有 个元，所以一共有 个布尔函数，数量十分惊人。所有的布尔函数都能用自变量和三个逻辑符号：与 ，或 ，非 来表示。戴德金提出了一个问题：在这 个函数中，有多少个是单调的？所谓单调，是指当我们把某个分量从 变成 后，函数值只能维持不变或者也从 变到 。 的时候自然两个常数函数都是单调的，而 时，有 这四个布尔函数，其中 显然不是单调的：从 变到 ，函数值则从 变到了 。所以有三个单调布尔函数，以此类推。 的情况也能像这样列举得出，但是再往上就越发困难了。下图展示了 到 的构造方法，其中 ， 用 表示，自变量则是 。
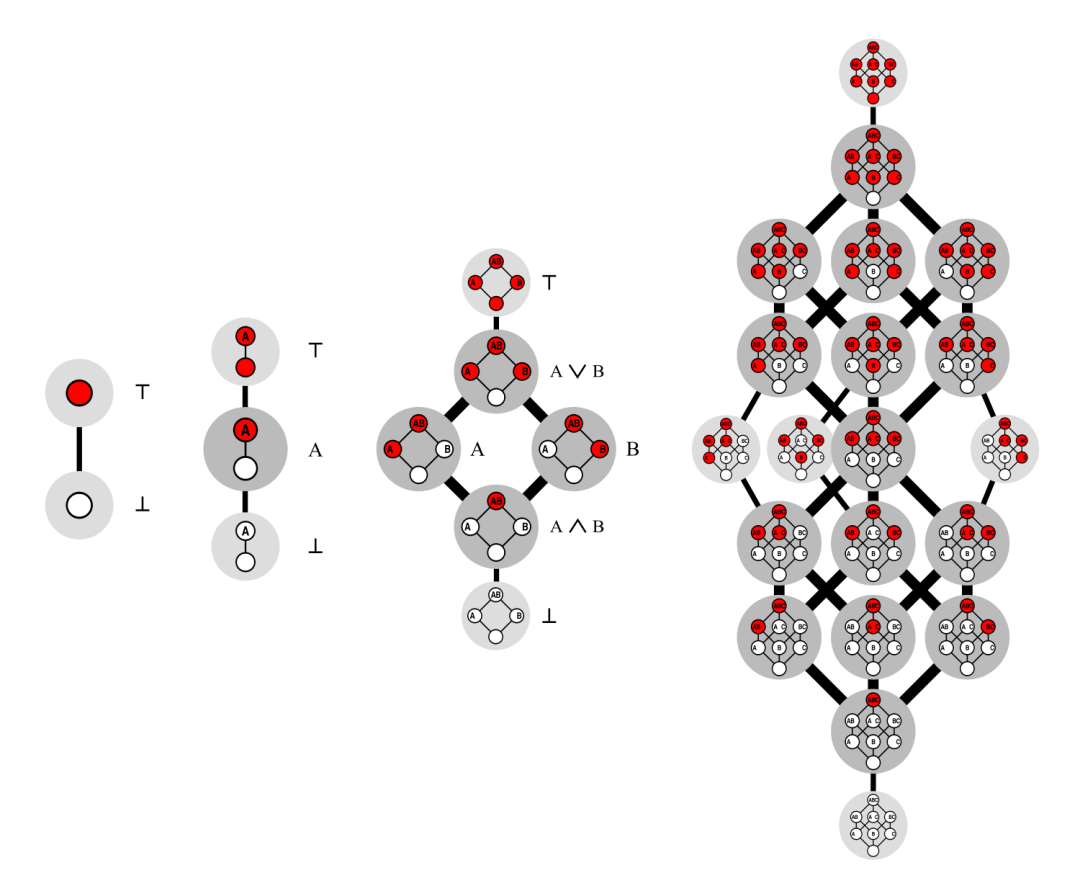图片来自维基百科
为什么要关心单调布尔函数呢？我们把所有单调布尔函数的集合记做 ，可以证明， 在 两个运算下是封闭的，并且满足分配律。这样的代数结构称为（分配）格（lattice），而最早研究这一结构的戴德金也被认为是格论的先驱。格论在抽象代数、逻辑学、理论计算机科学等领域中扮演着相当重要的角色。戴德金的格论研究却在他死后无人问津。直到上世纪30年代，美国数学家伯克霍夫（George David Birkhoff）在研究泛代数等过程中重新发现了戴德金的工作，从此格论才正式走向历史的舞台。戴德金本人未曾找到的第五个戴德金数也是在这一时期由美国数学家邱奇（Alonzo Church）找到。
从M(5)到M(8)
在寻找戴德金数之前，有一个相当现实的问题：要是戴德金数的增长速度与 相近，那么依靠现有的算力是根本不可能处理的。可喜可贺的是，数学家们证明戴德金数的增长近似于
所以即便是 ，近似于 ，只有76位数，远小于 的309位数。而 则近似拥有38位数，看起来就没有那么遥不可及了。
计数的困难在于，我们不可能把 个布尔函数全部遍历一次。邱奇计算 方法可以总结为分类相加。1946年，沃德（Morgan Ward）算出了 ，虽然他没有解释自己的方法，但他在论文中验证了邱奇的 。邱奇与另外两名数学家于70年代独立计算出了 。而 则是在1991年由魏德曼（Doug Wiedemann）给出，他的方法也与邱奇类似。
值得注意的是，这些计算本身并没有直接把所有单调布尔函数都找出来，而是通过单调布尔函数的一些性质以及对称性来直接计数。但是为了计算 ，很多时候我们需要知道 或者 中有哪些函数。事实上，已知的计算结果都用到了这样的方法。要想得到 ，就需要 中的函数表，这项计算也在90年代成功实现。但到了 ，计算机已经对于生成函数表束手无策了。所以在可见的未来， 的计算都不太可能实现。不过这并不意味着生成单调布尔函数表就是毫无意义的。近年来，生物学，图像处理等应用领域都在大量使用布尔函数，逻辑/代数这样的抽象领域越来越多地在现实世界中找到了自己的价值。
寻找M(9)的长跑
现在，我们看看是如何找到的。故事的起点在比利时的鲁汶天主教大学，当时还是计算机科学硕士生的范·赫图姆（Lennart Van Hirtum）正跟随考斯马克（Patrick De Causmaecker）教授研究毕业课题。考斯马克在2014年的一篇论文[3]中提出了一种新的通过 中函数表计算 的方法，称为 -系数公式。有了这个公式，就算是普通的家用笔记本电脑，也能在8分钟内计算出 。在考斯马克的指导下，范·赫图姆开始尝试用 -系数公式计算 。
当然事情没有那么简单。虽然用同样的方法可以在8分钟内计算出 ，但是到了 这，即便是粗略估计，按一般计算机也得运行数十万年。范·赫图姆在他的毕业论文中改进了公式，但最重要的，仍然是需要一台超级计算机。与深度学习不同，目前的GPU是对于计算 -系数并没有什么优势，而CPU的算力也无法指望。这时，他们想到了FPGA。
FPGA全称Field Programmable Gate Arrays，中文翻译为现场可编程逻辑门阵列。简单来说，这是一种半定制的集成电路，可以利用逻辑合成等工具快速把逻辑电路刻录上去，这样就能实现自己设计的并行算法。范·赫图姆一边进行着论文的理论设计，一边寻找着拥有FPGA的超级计算机。最终伸出援手的，是德国的帕德博恩大学。
超级计算机Noctua 2坐落于帕德博恩大学下属的帕德博恩并行计算中心。这台电脑拥有着世界上数一数二的大规模FPGA系统，而并行计算中心的负责人在了解范·赫图姆和考斯马克的意图后，欣然接受了他们的使用请求。对于他们来说，要用超级计算机来解决这样复杂的组合问题也是一项极具挑战性的任务，对于系统稳定性与可靠性提出了不小的要求，同时也是测试设备的绝佳机会。经过数年的开发，程序终于在去年开始运行。范·赫图姆也从鲁汶毕业，进入帕德博恩大学攻取博士学位。
程序运行了5个月，在2023年3月8日，终于得到了最终结果
同时到达终点
同样在计算 的，并不只有帕德博恩大学的这组人。德国德累斯顿工业大学的耶克尔（Christian Jäkel）也几乎在同一时间得到了相同的结果。耶克尔的计算基于 的函數表。他将问题转换为矩阵乘法，多台Nvidia A100 GPU总共花了5311小时，总计进行了4257682565次矩阵乘法计算之后，得到了与范·赫图姆等人完全相同的结果。耶克尔于4月5日将自己的论文[1]挂上了预印本网站，仅仅比帕德博恩的团队早了一天[2]。因此，发现 的殊荣将同时归于以上两组人，并且他们使用的不同方法更加证实了结论的正确性。不过他们都提到，目前的方法对于 还是不管用的。很难想象，当下一次的突破来临时，算力的发展将达到怎样惊人的程度。
参考文献
[1] Jäkel, Christian (2023-04-05). "A computation of the ninth Dedekind Number". arXiv:2304.00895 [math.CO]
[2] Van Hirtum, Lennart (2023-04-06). "A computation of D(9) using FPGA Supercomputing". arXiv:2304.03039 [cs.DM].
[3] Patrick De Causmaecker and Stefan De Wannemacker. On the number of antichains of sets in a finite universe, 2014.
[4] Yusun, T.J.: Dedekind numbers and related sequences (2008)
[5] Ninth Dedekind number discovered: Scientists solve long-known problem in mathematics, https://phys.org/news/2023-06-ninth-dedekind-scientists-long-known-problem.html
本文受科普中国·星空计划项目扶持
出品：中国科协科普部
监制：中国科学技术出版社有限公司、北京中科星河文化传媒有限公司
0
推荐
京公网安备 11010502034662号 