印度裔传奇统计学家C. R. Rao于2023年8月22日去世。他在1987年拉马努金诞辰100周年活动中,做了三次关于统计历史和发展的演讲,而每次演讲前都会提到拉马努金的生平和工作。这些演讲最后汇集成他的名作《统计与真理:怎么样运用偶然性》(Statistics and Truth, Putting Chance to Work),并把这篇拉马努金的回忆放在附录,以纪念这位伟大的印度天才数学家。
撰文 | C. R. Rao
被邀请为纪念拉马努金讲座的演讲者,我感到这是莫大的荣誉。我非常高兴地接受了这个邀请,特别还因为拉马努金(Srinivasa Ramanujan)的一生一直是激励我那个时代的学生们的一个伟大的源泉。正值这个伟大的天才诞生100周年,我们举行纪念活动有着多方面的深远意义。它提醒我们,始于发现基础的零和负数的印度数学传统依然存在。它也提醒年轻一代:他们能通过创造性的思维来丰富自己的人生。最后,我希望通过纪念活动能产生全国性的影响,让公众认识到数学的重要性,认识到数学是科学和艺术进步的一个关键因素,也提醒我们应尽所有的努力在我国鼓励数学学习和数学研究。
1986年,美国总统宣布每年4月14日-4月20日为全国数学认识周(National Mathematics Awareness Week),目的是让美国学生能保持学习数学的热情。苏联人造卫星的幽灵仍然在美国上空徘徊,任何忽视数学的倾向会被认为是对国家科学和技术进步的阻碍。比起宣告全国数学认识周来说,在印度我们更需要的是,公开承认我们还没有认识到我们的数学是多么薄弱。让我们通过纪念拉马努金诞辰100周年来促进印度数学的发展。我们不应让世人说:印度的数学从零开始,也以零结束。
因为拉马努金的一生与工作和我的演讲主题有关,我想借此机会介绍一些他的情况。拉马努金的出现如同数学太空中的一颗流星,划过短暂的人生,突然消失于他生命32岁那个时刻。在这个过程中,他把印度放进了现代数学的版图。拉马努金的数学贡献在很多领域内是深远的、永恒的,他是世界上最伟大的数学家之一。拉马努金并没有像通常的数学家那样去学习数学,而是发现和创造了数学。这使得他成为一个现象、谜一样的天才,而他的创作过程犹如一种虚构、一个神话。
拉马努金去世时留下了一份奇怪且罕见的遗产:写在三个笔记本和一些纸片上的约4000个公式。假设拉马努金的研究时间为12年,则他每一天就发现了一个新的公式或新的定理。这是任何一个从事创造性活动的人不能与之相比的。这些并不是通常的定理,它们中的每一个都是产生一个全新的理论的核心。这些公式和定理并不是凭空想像出来的一连串孤立的魔术般的公式,有的自身对今天的数学研究仍有深远的影响。更进一步说,在理论物理中从宇宙论的超凡理论到复杂的分子系统的统计力学,这些公式和定理在发展新概念方面同样具有深远的影响。1976年人们在剑桥三一学院的图书馆里,发现了他在健康逐渐衰弱时,留在130页没有编号的手写稿上的工作——这是他人生最后一年完成的。仅仅是在《补遗杂记》(Lost Notebook)中给出的结果,已经被认为“等价于一个伟大的数学家一生的工作”了。威斯康星大学的阿斯克(Askey)教授在评述拉马努金的贡献的独创性、深远性和永久性时说道:
他的工作乍一看来几乎是不可预测的。当了解其内容以后,仍可以保守地断言他的工作所涉及到的大部分内容,是任何生活在当今世纪的人不可能再发现的。而且,拉马努金发现的某些公式,至今没有人能理解或证明。我们恐怕永远不会了解拉马努金是如何发现这些公式的。
要理解拉马努金的创造性是困难的;在科学研究或艺术创作的纪要中不存在相似的记载。拉马努金发现的能支配整数无限集合的神秘定律和相关的关系,犹如一个科学家试图发现宇宙中隐藏的控制自然界事物的法则一样,这是几乎让任何一个科学家都感到敬畏和头疼的。让我们来看一看拉马努金在临去世之前的1919年所做的关于函数的一个猜想:如果一个整数可表为与顺序无关的几个非负整数的和,则可定义的组合形式为
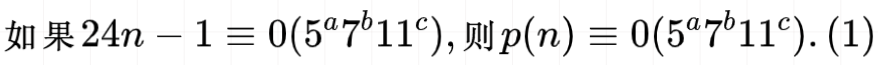
这个公式隐含着伟大的思想,而且这个结果的形式是一个美丽的发现,因为一个世纪以来,在椭圆函数或模函数的一般理论中没有产生任何这类的结果。另一个印度数学家乔拉(Chowla)证明这个猜想是错的,因为当时它不成立。由阿特金(Atkin, 1967)[Glasgow Math.J.,Vol.8,p.14-32.]证明,上述公式仅需稍加修正:
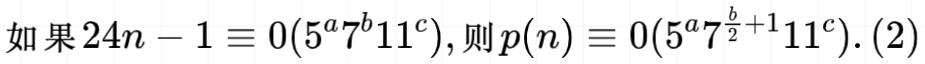
即公式(1)中第二行7的指数换为。如果拉马努金利用数学推导,或许他可以得到正确的结果,但他没有得到正确的公式这件事相对来说是不重要的;他的想象形成这样性质的结构,证实了这个发现背后他的思维过程无法解释。
一个人如何得到一个卓越的概念呢?需要做什么样的准备才能让头脑变得有创造力?一位天才是天生的、还是(后天)造就的?或许这些问题并没有明确的答案。然而,即便有答案,我们恐怕也不能解释拉马努金的大脑里为何能迅速地产生如此众多的卓越的想法。更使人感兴趣的是,因为拉马努金没有接受过正规的高等数学教育,从来没有着手过(现代)数学研究,也并不知道现代数学中研究问题的领域或方向。他叙述定理而没有给出证明,也没有指明动机。拉马努金无法解释他如何得到这些结果。他过去常说这些公式是拿摩卡(Namakkal)女神在梦中赐给他的。他常常一起床便记录下这些结果并迅速地验证它们,尽管有时并不能给出严密的证明。许多拉马努金陈述过的定理被证明是正确的。创造性是在潜意识层次上产生的吗?
马哈拉诺比斯(P. C. Mahalanobis)教授与拉马努金当年同期在英国剑桥。他总是讲述有关拉马努金的轶事,这些轶事由冉甘纳让(S. E. Ranganathan)记录在《拉马努金,普通人与数学家》(Ramanujan, the Man and the Mathematician)这本传记中了。这里我要引用一则冉甘纳让书中记载的轶事——正是由马哈拉诺比斯教授收集到的。
一次,我去他(拉马努金)的房间。那时正是第一次世界大战刚刚开始不久,我手里拿着一本月刊《海滨杂志》(Strand Magazine),那本杂志当时总登载难题让读者解答。拉马努金正在炉子上的锅里搅动着什么,准备我们的午饭。我靠着一张桌子坐下,翻阅着杂志。一道有关两个数的关系的问题引起了我的兴趣。问题的具体细节已经记不起来了,但我记得问题的类型。两个英国官员住在一条大街上两套不同的房子里,他们在战争中丧生;他们房子的门牌号数之间有某种特殊的关系,问题是求出这些数。这个问题并不很难。用反复试验法,我几分钟就得到了答案。
我说(开玩笑地):现在考你一个问题。
拉马努金:告诉我什么问题。(一边继续搅动锅。)
我读了《海滨杂志》上登载的问题。
拉马努金:请记下答案。(他给出了一个连分数。)
第一项是我得到的答案。其余各项就像街上的门牌号数无限增大一样,表为逐渐增大的具有同样关系的两个数之间的逐次解。我感到非常惊奇就问到:“你在一瞬间就得到这个答案了吗?”
拉马努金:当我听到问题时,即刻清楚地知道它的解显然是一个连分数;我就想:“这是一个什么样的连分数呢?”然后答案就出来了。就这么简单。
从冉甘纳让的记载里我们知道,拉马努金12岁时表现出了对数学的兴趣。据说当时拉马努金曾经问他在昆巴库纳市区高级中学高年级班学习的一个朋友,什么是数学中的“最高真理”。据说这个朋友给他提到毕达哥拉斯定理、股票和股份问题作为“最高真理”。毕达哥拉斯定理属于正统的数学,因为结论是在给定的前提下通过一系列演绎的推论得到的,不存在任何有关结论的不确定性问题。股票和股份问题属于概率,这里所得到的结论不一定要求必须准确,但是对投机者有帮助。两个问题都是学习上和研究中具有智力挑战性的领域。或许是比起股票和股份问题来说,拉马努金更熟悉毕达哥拉斯问题,这就使他迷上了数学。
拉马努金在笔记本上记录下来的绝大部分结果是无证明的,据说他用石笔在石板上进行推导,而仅仅把最后结果记录在纸上。当问他为什么不用纸时,拉马努金回答的是,他一周需要三令纸(译者注:令为量纸的单位,一令等于480张或500张),他没有钱来买那么多纸。
1914年拉马努金前往英国与剑桥著名数学家哈代(G.H.Hardy)一起工作之前,他在印度杂志上一共发表了5篇论文。由他独自署名或与哈代合作,他一生共发表了37篇论文。在他短暂的研究生涯内,这些论文发表的时间分布如下:

拉马努金死于1920年,时年33岁。在他生命最后的两三年里,他的健康状况越来越糟,但他仍继续进行研究并把很多结果记录在一个笔记本上,这个笔记本直到几年前才被发现。这个被称为《补遗杂记》的笔记本上有很多新的定理,其开创了数论研究的新领域。
当然,拉马努金是一个罕见的现象,他在或多或少的恶劣环境中开花结果——这样的环境中是一个常规的教育体系,旨在培养行政工作的所需的文书人员;贫穷迫使有天赋的学生放弃从事学术追求,并为谋生而求职,缺乏制度上的支持或其他研究机会。对于拉马努金在数学上的成就,尼赫鲁(Jawaharlal Nehru)在他《印度的发现》(Discovery of India)一书中写道:
拉马努金短暂的一生和他的去世是印度现状的一个代表。几百万人中有多少完全受到教育了呢?有多少生活在饥饿的边缘呢?如果对他们打开生活的大门,提供给他们食物、健康的居住条件、教育和成长的机会,这几百万人中会产生出多少杰出的科学家、教育家、技术工作者、企业家、作家和艺术家来帮助建立一个新印度和一个新世界呢?
尼赫鲁是一个理想家。确实,印度的状况这几年有了相当的改善。现在,印度科学的平均水平可以与任何发达国家相比。但是,人们总的感觉是:我们仍然没有达到完美和理想的水平。我希望,我们的政府和研究机构(在统计学家的帮助下!)进行调查研究,为把印度置于革新和科学发展的最前沿而做出必要的努力。
本文转载自微信公众号“和乐数学”,原文摘自《统计与真理:怎样运用偶然性》(科学出版社,2004)。《返朴》发表时略有改动。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 