在通用图灵机的基础上,数学家冯·诺依曼进一步发明了自复制机器,回答了生物学中最为深刻的一个问题:为什么所有生物都以DNA形式进行自我描述?图灵和冯·诺依曼,这两位计算机科学先驱偶然发现的生命奥秘并不广为人知,却为研究生物系统勾画出蓝图——把生命系统看作是计算机器。
这篇近期发表于PNAS的文章题为“图灵和冯·诺依曼的遗产:生命计算机的架构”,以DNA聚合酶为例,说明生物分子实际上就是计算机器;并阐释了计算模型的层级结构可以在生物计算领域找到类似结构。通过将生物学简化为计算形式,计算机科学可以用来将生物学系统化。反过来,计算机科学家或许能够挖掘生物计算中的自然宇宙,利用数十亿年的自然演化来发现新的计算模型或算法。展望未来,生物学和计算机科学可以看作是紧密相连的同一门学科,一门研究机器行为的学科。
撰文 | Hashim M. Al-Hashimi
翻译 | 汪显意
目录
摘要
1. 图灵的通用计算机(Universal Computing Machine)
2. 冯·诺依曼的通用构造机(Universal Constructor)
3. 分子计算(Molecular Computation)
4. 作为计算机的天然生物分子
5. 生物计算(Biological Computation)的一个具体例子
6. 生命计算机的层级
7. 解码生命计算

论文题目:
Turing, von Neumann, and the computational architecture of biological machines
论文地址:

摘要
20世纪30年代中期,英国数学家和逻辑学家艾伦·图灵(Alan Turing)发明了一种想象中的机器,它可以模拟人类计算者操纵有限符号装置(finite symbolic configuration)的过程。这一发明为现代可编程计算机提供了基础,从而开创了一个新的科学领域——计算机科学。十年后,在图灵机的基础上,美籍匈牙利数学家约翰·冯·诺依曼(John von Neumann)进一步发明了一种想象中的能够进行开放式演化的自复制机器。通过他的机器,冯·诺依曼回答了生物学中最深刻的问题之一:为什么所有的生物都以DNA形式进行自我描述?两位计算机科学先驱早在DNA双螺旋被发现多年之前,就偶然发现了生命的奥秘,但这个故事并不为人所知,甚至很多生物学家都不知道,你也不会在生物教科书中找到。然而,这个故事在今天和在八十年前一样重要:图灵和冯·诺依曼留下了研究生物系统的蓝图,即把生命系统看作是计算机一样。这种方法可能是回答生物学中许多问题的关键,甚至可能引领计算机科学的再进步。
几个世纪以来,人类文明一直痴迷于建造自动机,令它们通过遵循预定的指令集来执行机械操作。从布谷鸟钟到自动开启的寺庙大门,自动机被用作工具、宗教奇观和解释科学原理的原型。当人们可以用自动机来模仿动物的行为时,便会挑战 “某个东西是‘活的’意味着什么?” 这一说法。大约在20世纪中叶,冯·诺依曼开始对建造真正意义上“活的”自动机展现出兴趣:一个可以自我复制的机器,就可能进化成更复杂的机器。
冯·诺依曼被广泛认为是20世纪最有影响力的思想家之一,他对量子力学的数学基础做出了许多根本性的贡献,是博弈论的先驱之一,也是现代计算机逻辑和设计原理背后的主要架构师[1]。在20世纪40年代早期,冯·诺依曼开始对“控制论”[2]这一新兴领域产生兴趣,该领域关注于研究动物和机器的行为。由于两者都遵循逻辑和机械约束下的指令,控制论学者认为动物和机器在信息、通信和控制机制方面有很多共同之处。
在比较自然和人工机器时,冯·诺依曼发现一个有趣的现象,即生物体可以在几代之后演化成更复杂的生物体[3, 4]。他认为,这种行为很难被设计成一台人工机器。如果机器A要构造机器B,它必须包含完整的B描述。此外,A还必须包含额外的材料来管理B的构造。因此,B不可能比A更复杂,而随着一台机器建造另一台机器,自然的趋势将是退化。
1
图灵的通用计算机(Universal Computing Machine)
艾伦·图灵是20世纪的另一位思想巨人,也是计算机科学和人工智能的先驱,他还因在第二次世界大战期间破解纳粹密码(恩尼格玛)而闻名。为了设计一台可以构建更复杂机器的假想机器,冯·诺依曼从图灵那里获得了灵感,图灵几年前曾构想了一台假想的“通用”机器,可以计算任何其他机器可以计算的任何东西[5]。
图灵发明他的机器不是为了解决任何生物学中的问题,而是为了解决“判定问题(decision problem)”。这个问题被当时杰出的德国数学家大卫·希尔伯特(David Hilbert)称为“数理逻辑的主要问题”,它要求一种通用算法,可以通过有限的过程来决定一个任意的数学命题(陈述)是否可以使用逻辑规则从一组给定的公理中证明。公理是被认为是真的陈述。算法(algorithm)是一个遵循规则来寻找解决方案的系统过程。这个词来源于“algorithmi”,是“Al-Khwarizmi”的拉丁化版本,Al-Khwarizmi 是9世纪的波斯数学家,他首先引入算法来解决代数问题(代数 algebra 一词来源于阿拉伯语“al-jabr”,意思是“破碎部分的重新组合”)。当用特定语言表达时,算法被称为计算机程序。
冯·诺依曼以其数学证明能力而闻名。1926年,在评论希尔伯特的判定问题时,他猜想该问题的判定一定是否定的,但是“我们不知道如何证明这一点”。十年后,图灵证明了这个判定确实是否定性的。理论上的困难在于,人们必须从可以想象到的天文数字级的程序方案中尝试每一个程序,并证明它们都不起作用。图灵想出了一个绝妙的解决方案。将计算简化为简单机器可以执行的基本步骤。通过精确定义什么是可计算的,图灵用他的抽象机器证明了没有一种通用算法可以决定一个公式是否是可证明的。1936年,24岁的图灵发表了一篇具有里程碑意义的论文[5],这篇论文不仅解决了判定问题,而且可能更重要的是,为计算机科学的新领域和通用可编程计算机奠定了基础。
图灵想象中的机器由一条无限长的磁带和一个磁头组成,磁带被分成几段,磁头可以扫描磁带,一次写一个符号,并沿着磁带向右或向左移动一段。为了“记住”它从一个步骤到下一个步骤所做的事情,图灵允许机器具有不同的“状态”,他设想这些状态代表一个人执行计算时不同的意识状态。然后,机器遵循以转换表形式给出的一组规则,该转换表为每个初始状态和扫描到的符号指定了特定操作(例如,将磁头向左或向右移动一段,或者写入“0”或“1”)及其最终状态。例如,一个规则可能是:“如果磁带磁头处于状态A并扫描0,请将磁头向右移动一段并键入1,然后将其状态更改为状态B”。转换规则还可以指示机器不改变状态或完成并停止操作。依照转换规则,机器根据扫描获得的符号从一个状态跳转到另一个状态,每次执行不同的操作。计算的输入是写在磁带上的原始符号,而输出则是当机器最终停止时写在磁带上的任何东西。
尽管它很简单,但图灵证明了他的机器可以执行一台机器可以执行的任何计算。所需要做的就是向他的机器提供另一台机器的描述,他就可以通过将另一台机器的转换表编码到磁带上来完成。描述机器的转换表本质上就是机器本身,并且可以有无限多个可能的转换表来对应无限多个不同的机器。这种广义计算模型被称为“通用图灵机”(Universal Turing machine),它形成了现代通用可编程计算机的理论基础。
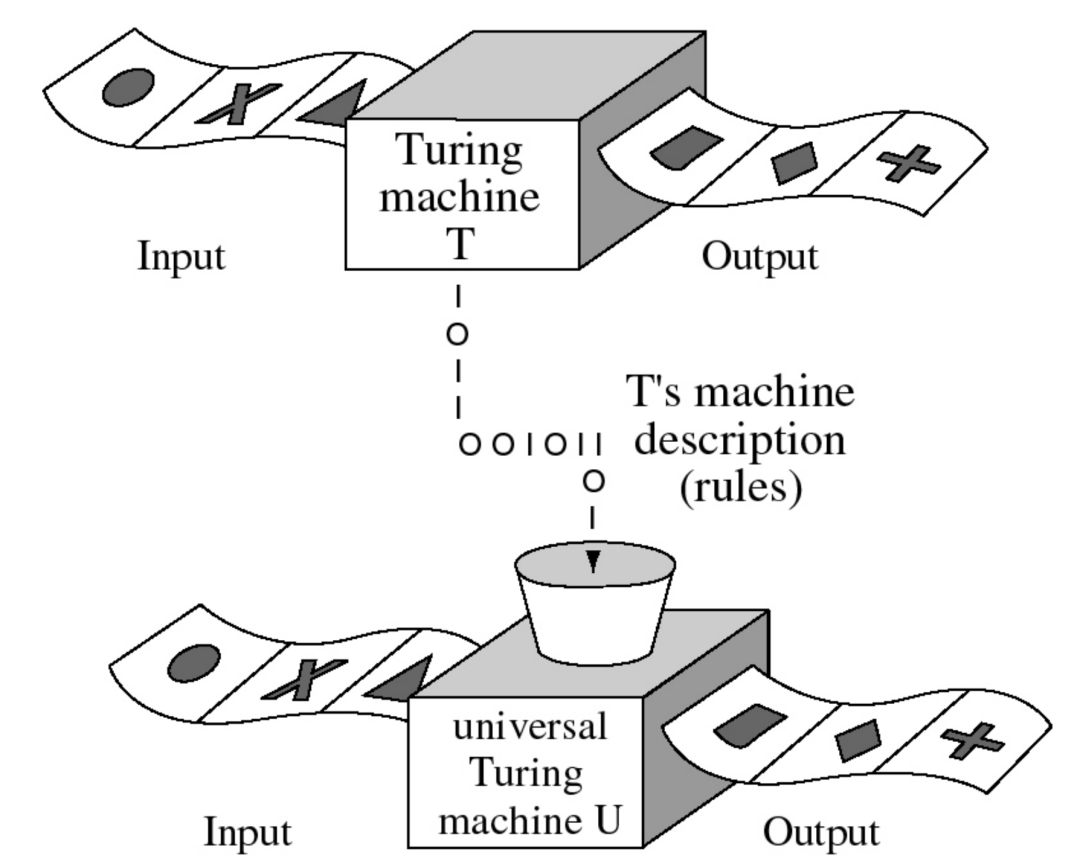
图1. 通用图灵机(Universal Turing machine)
图灵可以用他的抽象机器来枚举所有可能的算法,并证明判定问题没有解决方案[5]。假如这样的算法确实存在,那么就有可能对图灵机进行编程,以预测第二台图灵机是否会在给定任意输入后最终停止运行或陷入恶性的无限循环。图灵证明了这样的图灵机在逻辑上是不可能的。他使用了一种称为归谬法或反证法(reductio ad absurdum)的策略。他假设存在这样一台停下来的机器,然后证明将这台机器喂给自己会导致矛盾。
图灵在证明过程中把机器喂给它自己,在这个过程中引出了自指(self-reference)概念,这并非巧合。在20世纪初,自指的命题产生了悖论,并在数学领域造成了严重的破坏,对希尔伯特本人热情拥护的正统的公理系统所具有的一致性和完备性提出了质疑。在图灵开始研究他的机器几年前,奥地利逻辑学家和数学家库尔特·哥德尔(Kurt Gödel)给出了关于自指的命题:“这个命题是不可证明的”,表明并非数学系统中的所有正确命题都可以从公理中证明[6],此举震撼了数理逻辑的核心基础。冯·诺依曼在设计他的自我复制机器时,同样遇到了处于分子生物学核心位置的自指问题。
2
冯·诺依曼的通用构造机(Universal Constructor)
为了建造一台能够演化出更复杂机器的通用自复制机器,冯·诺依曼意识到他需要扩展图灵机的概念,使之可以输出另一台机器,而非打印一串1和0的磁带[1]。冯·诺依曼设想了一台由三个部件组成的机器:一个描述机器的“蓝图(blueprint)”,就像图灵磁带一样,里面有如何建造另一台机器的指令;一个通用的“构造机(constructor)”,用来解码构造机器的指令;还有一种通用的“复制机(copying machine)”,可以复制这些指令[3, 4]。机器使用这些指令复制自己,然后复制这些指令,再将它们输入新机器,以此类推。
为了使这台机器能够制造出超越其自身复杂性的机器,冯·诺依曼还加入了另一个关键因素。40年前,荷兰植物学家雨果·德弗里斯(Hugo de Vries)发现,一种新形态的月见草可以随机自发生长,并繁殖许多代。他为这样的变化创造了一个新词:“突变(mutation)”。正如自然界中的突变可以自发产生一样,冯·诺依曼允许复制机在复制指令时出错。复制错误有可能导致机器产生可执行的变种,那么就可能通过自然选择演化出更复杂的机器。
我们现在知道,生物体就是冯·诺依曼的自我复制机器在真实生命中的一种实现。以DNA序列形式携带指令的遗传磁带首先被转录成相应的信使RNA磁带,然后输入到一个通用的构造机——“核糖体”中,核糖体将RNA信息翻译成相应的氨基酸序列,这些氨基酸序列指定了蛋白质磁带。反过来,蛋白质磁带会自发地折叠成分子装置,为细胞提供主要的功能。当生物体繁殖时,DNA磁带被聚合酶复制并从父母传给后代,这就解释了遗传是如何工作的。复制DNA时可能会发生错误,导致生物种群多样化。最终,一些突变会展现出一种优势,经过几代的演化,那些具有优势的生物体会迅速繁殖并占据整个种群。这种突变和自然选择的循环就是生物学家所说的“达尔文进化论(Darwinian evolution)”——这个过程标志着生物学和生命的开始。从DNA到RNA,再到蛋白质的信息流,就是弗朗西斯·克里克(Francis Crick)所说的“分子生物学的中心法则(Central Dogma of Molecular Biology)”[7]。
1948年9月20日,在加州理工学院举行的“大脑行为机制的希克森研讨会”上,冯·诺依曼在一次演讲中描述了他的自复制机器[1, 3](图2)。这是在DNA双螺旋结构被发现的5年前[8],在克里克提出分子生物学的中心法则的12年前[7]。那时,DNA还是遗传信息载体的主要竞争者。

图2.(左)1948年宣传希克森研讨会的传单。(右)与会者合影。后排从左到右分别是 Henry W. Brosin,Jeffress,Paul Weiss,Donald B Lindsley,John von Neumann,J. M. Nielsen,R. W. Gerard,H. S. Liddell。前排分别是Ward C Halstead,K. S. Lashley,Heinrich Klüver,Wolfgang Köhler 和 R. Lorente de No。图片由加州理工学院档案管理员Loma Karklins提供。
包括冯·诺依曼的演讲在内的研讨会内容于1951年被集合成书[3]。根据演讲稿,冯·诺依曼清楚地看到了他的自复制机器和生物体之间的联系,他指出,“……指令ID大致影响基因的功能。同样清楚的是,复制机B执行繁殖的基本行为,即遗传物质的复制,这显然是活细胞增殖的基本操作。也很容易看出,系统E,特别是ID的任意改变,如何能表现出某些典型的性状,这些性状与突变有关,通常是致命的,但有也有可能继续繁殖。”
冯·诺依曼认为,为了实现自我复制,人们需要一种机制,不是复制机器本身,而是复制一套建造机器的指令,在这一点上,冯·诺依曼的非凡洞察力是公认的。他的逻辑依据是,机器是“变化和反应”(varying and reactive)的,仅仅观察它就可能导致难以预见的变化。相反,指令带是“准静态的”,并且不太可能随着观察而改变。因此,由于生物体需要复制,它们会携带构建自身的指令,而指导如何构建生物体的指令会比生物体自身的指令更精确地被复制。
今天,我们认为指令是复制来的是非常自然的。指令确实指导机器如何构建指令自身。冯·诺依曼认识到,这样一个方案会导致一个自指类型的深层逻辑问题。指令必须包括用于构建指令本身的附加指令(称为A)。然而,因为A是机器的一部分,所以需要提供指定如何制造A的附加指令B。但是接下来,需要C来描述B,以此类推。这最终陷入了一个“恶性循环”,如同一幅包含自身副本的图片,永无止境。冯·诺依曼将指令与机器的其余部分分离,并采用一个单独的设备来复制指令,从而避免了这种恶性循环。复制不需要额外的指令,一个模具本身就提供了铸造一个雕塑而非其他东西所需的信息。DNA就是自身复制的模版。
通过他的机器,冯·诺依曼回答了生物学中最深刻的问题之一:为什么所有的生物体都以遗传分子——如复制的DNA——的形式携带自我描述并传递给后代?这一特性将生物与非生物区分开来,将生物学与所有其他学科区分开来。许多无生命的自然系统是复杂的;但只有生物才能自我描述(self-description)。冯·诺依曼的机器告诉我们,我们自身携带着自我描述的信息,因为指令可以比有机体本身更精确地进行复制,而复制错误或突变导致的变异是进化的基础。DNA的复制是为了避免陷入自指恶性循环的困境。冯·诺依曼不仅为生物学中最大的革命之一奠定了基础,而且他还告诉我们生物体为什么是一种基于逻辑原理而以如此的构造链接起来的机器。
通过回顾我们得知,很明显,冯·诺依曼的演讲几乎没有在生物学界产生影响。希克森研讨会的与会者和组织者之一,著名化学家莱纳斯·鲍林(Linus Pauling)几年后将他的注意力投入到解决DNA的结构问题上[9],但他从未提及冯·诺依曼的工作。分子生物学的先驱之一西德尼·布伦纳(Sydney Brenner)是一个明显的例外。早在1952年,他就注意到了冯·诺依曼的工作,但用他自己的话说:“……当时的我还不够聪明,没有真正意识到这就是DNA和遗传密码的全部内容。”西德尼也是最早发现DNA双螺旋结构的科学家之一。他说,当他在1953年第一次看到双螺旋的时候,就想到了生物信息的概念和它与冯·诺依曼的自复制机器的联系[10]。西德尼没有错过见证冯·诺依曼和图灵的工作,赞美它们对于生物学的影响[11],但这似乎也没有对今天的生物学界产生什么影响。
3
分子计算(Molecular Computation)
我们能把生物体和计算机之间的这种类比推广到多远呢?每一种生命现象,包括我们如何感知世界,都源于细胞内生物分子的行为和相互作用。如果这些生命成分的基本行为可以用计算机来描述,那么我们所称之为生命的一切都必然是计算的产物。大自然有没有发明一些生物分子来实现分子计算呢?如果有的话,这些计算解决了什么类型的问题?
生物计算简史
生物分子是计算机器的想法可以追溯到20世纪60年代初,当时生物学家弗朗索瓦·雅各布(Francois Jacob)和雅克·莫诺(Jacques Monod)提出,生物分子可以执行编程语言常见的条件语句来控制细菌中的蛋白质生产。在20世纪70年代,查尔斯·贝内特(Charles Bennett) 将RNA聚合酶(将DNA转化为信使RNA)与图灵机进行了比较,推测分子可以是更节能的计算机器[13]。但伦纳德·阿德曼(Leonard Adleman)又花了20年时间才展示了分子计算的第一个真实的例子,使生物分子作为计算机器的概念具体化。
Adleman利用DNA单链可以结合形成DNA双链的特殊性质,解决了一个被称为“旅行商问题”的算法问题[14]。这个非平凡的问题要求在航线连接的城市之间找到最短路径,并且每个城市恰好经过一次。通过创造代表城市和航班的DNA分子,然后在试管中组合它们,他可以在几分钟内得到答案。
Adleman的工作以后,分子计算已经被用于解决各种算法问题,例如哈密顿路径问题(Hamiltonian path problem)[14],布尔可满足性问题(Boolean satisfiability problem)[15]和骑士放置问题(knight placement problem)[16]等。此外,分子计算已被用于从分子和生物砖(biological building blocks)开始设计复杂的逻辑电路,使其能够应用于药物筛选、环境监测和疾病诊断[17]等方向。
天然分子(biomolecules)也可以做生物计算吗?
尽管在分子计算方面取得了非凡的成就,但大多数生物学家并不认为生物分子是计算机器,也不认为它们催化的生化反应是一种计算形式。结构生物学是一个试图通过在原子尺度上确定生物分子的3D结构来理解它们如何工作的领域,在结构生物学发表的大多数论文中,你不会找到计算机科学语言。结构生物学家尚未接受生物分子作为计算机器的概念,因为迄今为止实现所有的分子计算都依赖于工程生物分子解决算法问题,这些问题与天然生物分子几乎没有相关性,并且在自然界的生物分子中也没有明确的类似物。因此,虽然我们可以用能够解决哈密顿路径问题的生物分子来设计计算机,但我们在自然界的生物分子中同样找不到这样的程序。
系统生物学
然而,几十年来我们已经知道天然生物分子可以用来处理信息。在20世纪60年代早期,弗朗索瓦·雅各布(Francois Jacob)和雅克·莫诺(Jacques Monod)对乳糖操纵子(lac operon)进行了开创性的研究,揭示了细菌如何根据糖浓度来调节负责糖分解的酶的水平。在这里,一种对糖酶特异的阻遏蛋白与相应基因的DNA结合,阻止RNA聚合酶产生糖酶的mRNA。糖分子与阻遏蛋白结合,使其从DNA上脱落,从而产生mRNA和酶。一旦糖分子被消耗,阻遏蛋白就返回到DNA,又会阻断糖酶的合成。重要的是,这不仅仅是一个开关。通过确定阻遏蛋白分子停留在DNA上或离开DNA的时间比例,糖浓度非常精确地将酶的水平调整到所需,从而建立了一个精确的反馈回路。
在过去几十年里,系统生物学领域已经发现了生物系统中使用的大量逻辑电路,揭示了细胞内信息处理的大量并行性,这是冯·诺依曼当时的思想没有完全捕捉到的。因此,系统生物学已经将生物分子的信息处理能力建立在坚实的数学基础上,并且揭示了那些只能通过将生物系统整体地视为许多相互作用的生化反应的网络来进行建模才能进行解释的行为[18-20]。这种系统性的方法已经解决了生物学中的许多基本问题,例如,结构、振荡或波如何在同质环境中出现。图灵在他生命的最后阶段为这些努力做出了贡献。在20世纪50年代早期发表的另一篇具有里程碑意义的论文中,他从理论上展示了两种化学物质或“形态发生素”(morphogens)如何相互扩散和反应,从而产生空间斑图,就像豹子皮肤上的斑点从均匀同质的状态所展开的排列一样。
因此,几十年来,分子生物学中的信息处理已经被明确地解决了很多次。然而,尽管系统生物学取得了巨大的进步,生物分子仍然通常被视为将输入转换为输出的黑盒,而没有提供有关计算其基本步骤的分子描述。我们可能知道软件,但缺乏对机器的硬件描述,来说明一个生物分子的序列是如何决定它是怎样处理信息的。结构生物学领域通常提供完成生化反应所需的各种微观基本步骤的详细原子描述,但却很少有人尝试将天然生物分子的这种行为置于计算机器的背景之下。
4
作为计算机的天然生物分子
图灵在描述计算所需的原材料时,不知不觉地描述了所有天然生物分子的行为。就像图灵机一样,生物分子在“扫描”(scan)底物时,也会在不同的构象(conformational)或化学“状态”(states)之间转换。每完成一次不同的操作,比如添加或删除一个化学基团,就发生一次这样的转换。正如算法需要一系列合乎逻辑的顺序步骤来找到解决方案一样,生物分子也需要经过许多逻辑的和顺序的步骤来催化多步骤的生化反应。因此,生物分子的行为方式是因为它们是计算机,它们催化的反应是一种计算形式。
底物扫描
为了方便起见,图灵将写在2D纸上的信息简化为1D磁带上包含若干0或1的线性数组。然后采用连续的观察来扫描磁带,一次一个字符。图灵认为这样设置比较合理,因为冗长的符号很难“一眼”看到。生物分子还通过一种称为“分子识别”(molecular recognition)的过程扫描底物分子。与图灵机不同的是,它们一次观察底物分子上的几个官能团(符号)。此外,符号不限于二进制(0或1),也不必须以1D形式排列。相反,大自然在3D场景将数百种不同的化学基团链接,创造出数千种形状、大小和电子特性不同的底物。然后,生物分子通过活性位点与底物进行物理结合,从而一目了然地解码该3D信息。这些活性位点具有最佳定位的功能基团,可以与底物上的化学基团相互作用。
当正确的底物以正确的方向触及活性位点,就会像钥匙插入锁一样,识别并粘着在生物分子上,进而引发可产生计算行为的变化。其他分子会被弹开,不起作用。大自然使用分子扩散作为一种非常有效的机制来穿越短距离,也作为回路连接的一种更经济的替代品。蛋白质扫描细胞环境中大量的底物分子,每秒钟被来自四面八方的底物分子不断轰击数万亿次。
有序操作
生物分子通常在一个底物上执行一种特定的操作,比如,破坏一个特定的键,之后释放产物。那么,生物分子如何执行复杂计算所需的多个有序操作呢?演化发明了一个巧妙的解决方案:使一个生物分子的产物成为另一个生物分子的底物,如此进行下去。在生物计算中,磁带可以从操作一个转换表的一台机器上掉下来,并跳到操作第二个转换表的第二台机器上。
状态和记忆
通过赋予机器多种状态,图灵在不知不觉中解释了生物分子最神秘的特性之一。教科书将DNA等生物分子描述为静止的物体,但事实并非如此。在短短一秒钟内,DNA就会自发地转变成数千种不同的结构,称为“构象状态”(conformational states)。甚至它的化学成分也可以通过表观遗传修饰(epigenetic modifications)而改变。因此,虽然我们可以为一栋建筑绘制建筑蓝图,但当涉及到生物分子的分子世界时,我们需要指定一个具有许多不同构象和化学可能性的景观,每种可能性都有特定的概率[22]。这种景观使生物分子能够在不同的状态之间转换,这是图灵机的基本特征。
图灵机模型告诉我们,生物分子之所以可以形成不同的状态,是因为它们提供了一种记忆形式,使它们能够在从一个逻辑步骤移动到下一个逻辑步骤时“记住”自己在做什么。事实上,可以存储的信息量与状态数之间存在简单的数学关系。一个比特的内存有两个状态,两个比特有四个状态,n个比特有2n个状态。因此,具有n个构象或化学状态的生物分子可以编码log2(n)比特或log256(n)字节的信息(1字节有28=256个状态)。在热力学领域,log(n)也被称为熵,是无序的度量。然而,正如我们将看到的,要想把这个潜在的巨大的构象状态库作为一种记忆形式来访问,需要有专门增加给定状态概率的方法。
图灵还告诉我们,生物分子改变状态是为了“改变它们的意识状态”。因此,根据其状态的不同,相同的生物分子可以执行不同的任务。例如,DNA的双螺旋结构用于存储遗传信息,但复制DNA则需要单链结构。因为不同的构象和化学状态以不同的概率发生,所以生化反应的命运并不是一成不变的,而是可以分支成具有不同概率的几种不同结果。这些结果中包括一些罕见事件,例如复制DNA时的复制错误,这可能导致对生命和演化至关重要的突变。由于生物分子的行为和它们所催化的反应是概率性的,我们永远无法预测动物的行为;我们所能做的就是把概率归于未来事件。
5
生物计算(Biological Computation)的一个具体例子
为了让大家相信生物分子实际上就是计算机器,我尝试把生物分子的行为简化成一个逻辑转换表,就像图灵为他的机器选择的那样。我选择了冯·诺依曼磁带自复制机的生物学类似物——DNA聚合酶,这种酶的任务是复制DNA,在进化中处于中心地位。
像图灵机一样,DNA聚合酶通过连续观察来扫描DNA模板链中的核苷酸,将遇到的每个核苷酸放入其结合口袋(binding pocket)中。然后,聚合酶通过与溶液中的核苷酸三磷酸单体分子G、C、A和T物理结合,和结合袋中的核苷酸形成碱基对,从而实现对它们的扫描。之后聚合酶合并(“写入”)结合的核苷来合成互补的DNA链副本。为了完美地复制DNA,聚合酶必须只合并满足沃森-克里克配对规则的单体:如果核苷酸是“G”则结合“C”,如果是“C”则结合“G”,如果是“A”则结合“T”;否则拒绝该单体。但是聚合酶不能“看到”单体;那么它是如何实现这些规则的呢?
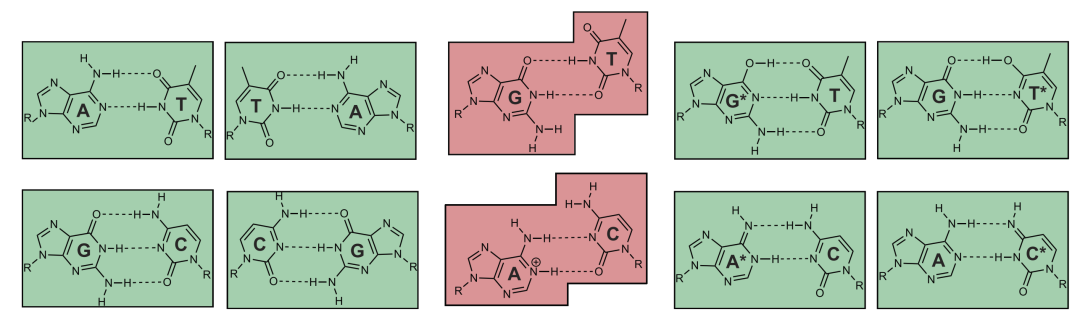
图3.(左)典型的沃森-克里克碱基对形成一个矩形,被称为“沃森-克里克几何”(Watson–Crick geometry)。(中)非经典错配,如G-T和A-C,形成被称为“摆动”(wobble)构象的非沃森-克里克几何形状。(右)错配,可以通过碱基的互变异构化(tautomerization of the bases)(用星号表示)得到类似沃森-克里克几何的形状。
沃森-克里克碱基对都有一个共同的矩形形状,而所有其他错配的碱基对,如G-T和A-C形成一个不规则的几何形状(图3),聚合酶使用这些几何差异来区分正确(矩形)和不正确(不规则)的单体(图3)。然后,聚合酶周期性地通过一系列构象来实现转换规则“只接受形成矩形碱基对的单体”。下面是它的工作原理。
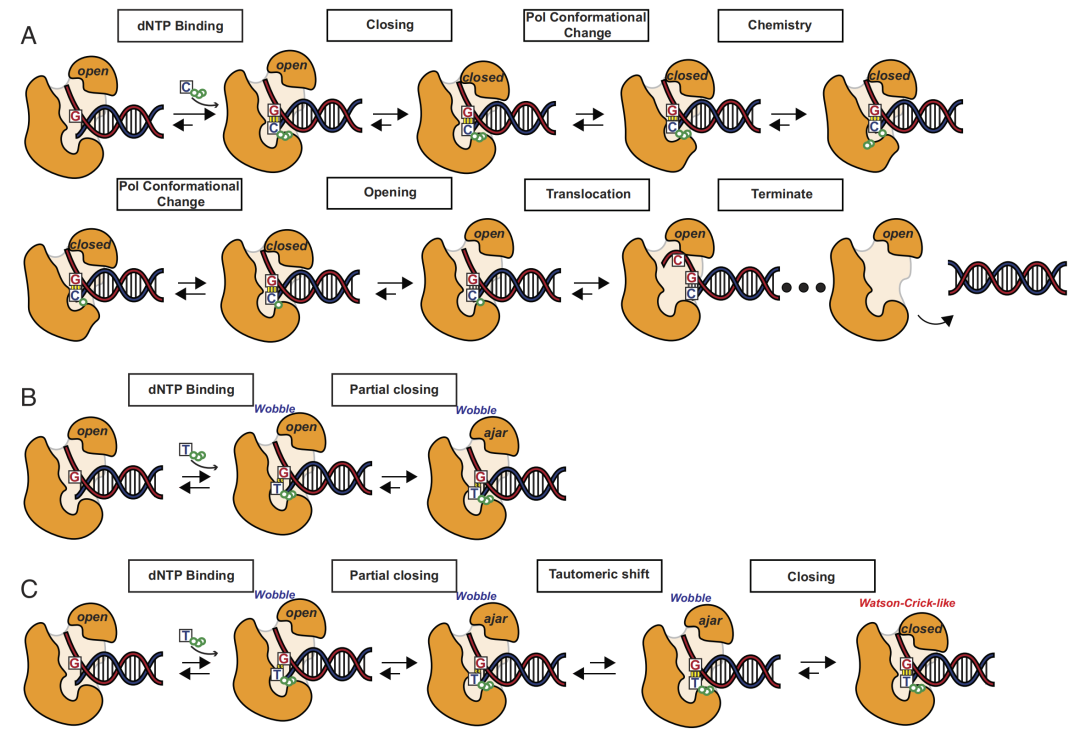
图4. 高保真DNA聚合酶的核苷酸合并机制。注意,这个机制可以因聚合酶而异。给出的实例代表聚合酶β和ε的机制[23-25]。(A)沃森-克里克碱基对的正确合并。(B)诱导拟合子程序增加了高保真聚合酶合并核苷酸的精度。(C)通过碱基互变异构实现的错配可导致复制错误,如果不加以纠正就会导致突变。
聚合酶构象景观包括:高度可能的“打开”状态,其中盖子(lid)打开,允许单体进入;和一个不太可能的“关闭”状态,其中盖子关闭,阻止单体进入(图4A)。当正确匹配的核苷酸进入结合口袋时,它与模板链中的核苷酸形成矩形沃森-克里克碱基对。沃森-克里克碱基对倾向于关闭盖子,就像盖子与匹配的容器合在一起一样。因此,闭合状态现在是最可能的构象(图4A)。这就是聚合酶如何执行转换规则:“如果碱基对具有矩形形状,则关闭盖子”:
初态 | 输入 | 操作 | 终态 |
开 | 矩形 | 关闭盖子 | 关 |
就像图灵机一样,关闭状态允许聚合酶“记住”:它已经消耗了正确的单体。关闭状态存储这个中间结果。处于关闭状态的聚合酶在其活性位点有正确的单体结合作为输入,转变为具有催化活性的构象状态(图4A)。因为只有正确的沃森-克里克碱基对才能通过这一步,它有助于防止错配的碱基对进行合并。此行为由以下转换规则描述:
初态 | 输入 | 操作 | 终态 |
关 | 矩形 | 形成催化结构 | 催化剂 |
一旦处于催化活性状态,单体就被化学连接并合并到DNA链增长中的互补拷贝链中(图4A)。其他所有的步骤都是可逆的,而只有这个步骤不可逆并且消耗能量,因为它需要产生信息并熵减。能量由进入的核苷三磷酸单体以化学键的形式提供,当单体合并时,化学键断裂,释放其合并所需的能量(图4A)。这种能量还可以帮助引导聚合酶沿着DNA磁带移动,这样它就可以按照下面所描述的事件序列扫描下一个核苷酸。
状态 | 行为 | ||
初态 | 输入 | 操作 | 终态 |
催化剂 | 矩形 | 结合核苷酸 | 催化剂 |
合并的单体作为输入与未合并的单体不同。合并的单体在催化状态下引发不同的行为,导致聚合酶撤销催化结构并回到关闭状态(图4A):
状态 | 行为 | ||
初态 | 输入 | 操作 | 终态 |
催化剂 | 合并的单体 | 恢复关闭 | 关 |
区分合并的和未合并的单体在逻辑上很重要,否则,聚合酶将停留在催化状态,无法回收或无法与后来的单体合并。同样,合并的单体必须在关闭状态下引发新的响应,否则,如果按照未合并的单体处理,聚合酶将在关闭状态和催化状态之间一直循环下去,计算机科学家称之为“死循环”。实际上,关闭状态通过转变为开放状态而不是催化状态来响应合并的单体(图4A)。
状态 | 行为 | ||
初态 | 输入 | 操作 | 终态 |
关 | 合并的单体 | 打开盖子 | 开 |
最后,合并的单体还引发不同于开放状态的行为,使得DNA聚合酶沿着DNA移动一个位置以扫描下一个核苷酸(图4A)。
状态 | 行为 | ||
初态 | 输入 | 操作 | 终态 |
开 | 合并的单体 | 改变位置 | 开 |
此时,所有中间结果都将被丢弃,从而为第二个周期释放内存。这个循环不断重复,直到聚合酶遇到空白,复制过程停止。当DNA聚合酶程序运行时,计算的结果是DNA链的一个互补副本链。
诱导配对的子程序
像许多酶一样,聚合酶非常精确,平均每复制10万个字母中只会出现一个错误(注:这只反映了核苷酸的错误结合,不包括校对)。聚合酶采用另一套涉及不同构象状态的转换规则来主动拒绝不正确的单体。许多酶使用的这种子程序被称为“诱导配对”(induced- fit)。下面是它的工作原理。
当不正确的单体结合到聚合酶口袋时,它与模板核苷酸配对,形成不匹配的碱基对,具有不规则的非矩形形状。这种错配使盖子无法完全闭合(图4B),它只能部分关闭以形成“半开”(ajar)的状态:
状态 | 行为 | ||
初态 | 输入 | 操作 | 终态 |
开 | 不规则形状 | 部分关闭盖子 | 半开 |
作为构象景观中的另一种状态,半开状态是无活性的,不能合并单体(图4B)。如果不正确的单体结合到口袋,聚合酶使用半开状态来主动引诱构象远离催化活性的闭合状态。然后半开状态又恢复到打开状态。
状态 | 行为 | ||
初态 | 输入 | 操作 | 终态 |
半开 | 不规则 | 打开盖子 | 开 |
部分关闭然后打开的循环一直持续,直到不匹配的单体最终从口袋里掉出来,这个过程可以重新开始。
状态 | 行为 | ||
初态 | 输入 | 操作 | 终态 |
开 | 矩形 | 关闭盖子 | 关 |
开 | 不规则 | 部分关闭盖子 | 半开 |
开 | 合并的单体 | 移动一个位置 | 开 |
开 | 空白 | 停止 | 停止 |
关 | 矩形 | 形成催化结构 | 催化剂 |
关 | 合并的单体 | 打开盖子 | 开 |
催化剂 | 矩形 | 合并核苷酸 | 催化剂 |
催化剂 | 合并的单体 | 恢复关闭 | 关 |
半开 | 不规则 | 打开盖子 | 开 |
半开 | 矩形 | 关闭盖子 | 关 |
表1. 高保真DNA聚合酶合并核苷酸的转换表,不包含动力学校对(kinetic proofreading)所需的指令。
复制错误
为什么DNA聚合酶在极少数情况下会出现复制错误呢?这些随机错误使冯·诺依曼的机器实现了开放式的演化。因为生物分子不断地在各种构象状态之间扭曲,在分子计算的世界里,机器和输入并不是一成不变的。在极少数情况下,它们可以改变。
例如,在极少数情况下,G单体可以经历涉及单个氢原子重新定位的化学变化(图4C)。所得的烯醇形式 Genol 在化学上类似于A,因此可以与T配对以形成近乎完美的矩形碱基对(图4C)[27]。伪装成矩形碱基对,Genol-T错配欺骗聚合酶打出错别字,打出“G”而不是“A”(图4C)。如果不加以纠正,这样的错别字将导致突变。这种“互变异构”变化是很难出现的(概率通常为1/100000)[28],这就解释了为什么突变很少发生。它们随机发生,这就解释了为什么突变是偶然事件。蛋白质的3D结构也有一定概率发生转变,从而产生不同的结果。通过这些构象波动,生物体成为了非确定性机器。
执行“复制DNA”算法的DNA聚合酶的逻辑行为可以简化为一个转换表(表1)。复制DNA的算法也可以用计算机科学里的“状态图”(state diagram)(图5A)来描述,这与生物化学家所说的“动力学机制”(kinetic mechanism)有很多共同之处。如果我们深入观察,每个生物分子都可以简化成一个描述其逻辑行为的转换表;因此,每个生物分子都可以被描述为一台计算机器(图5B)。
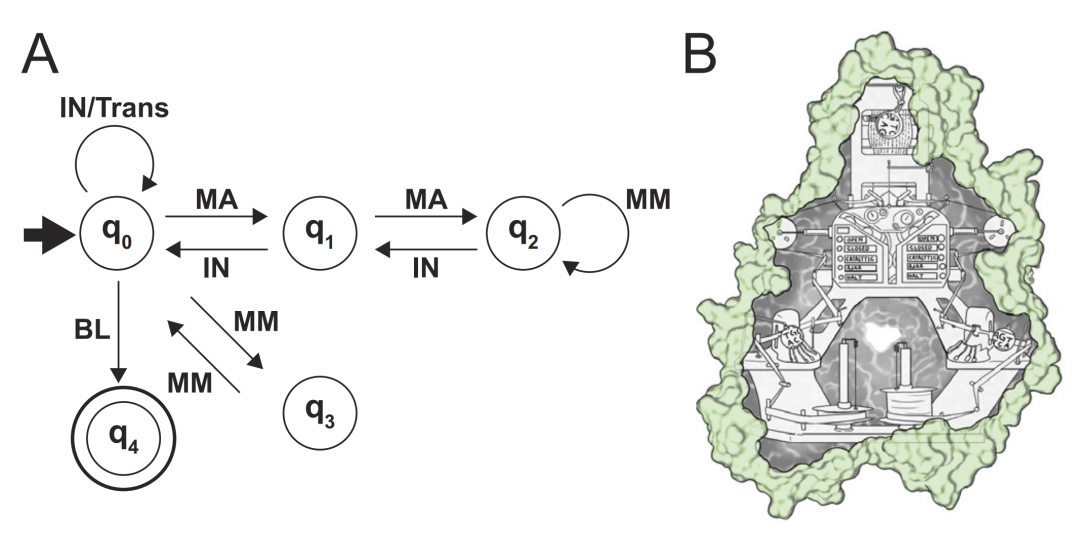
图5. DNA聚合酶是一种有限状态机。(A)DNA聚合酶合并核苷酸的有限状态机的状态图。q0、 q1、 q2、 q3和q4分别表示DNA聚合酶的开放、封闭、催化、半开放和停止的状态。输入为MA =匹配(矩形);MM =不匹配(不规则);IN =合并;BL =空白。注意,q0通过移动位置(Trans)处理输入“IN”,然后返回到状态q0。(B)DNA聚合酶作为计算机的图形描述。
6
生命计算机的层级
计算机科学家已经详细阐述了一个越来越强大的计算模型的层级结构,这些模型采用了越来越复杂的记忆形式(图6)。许多这样的机器都能在生物计算领域找到类似结构(图6)。
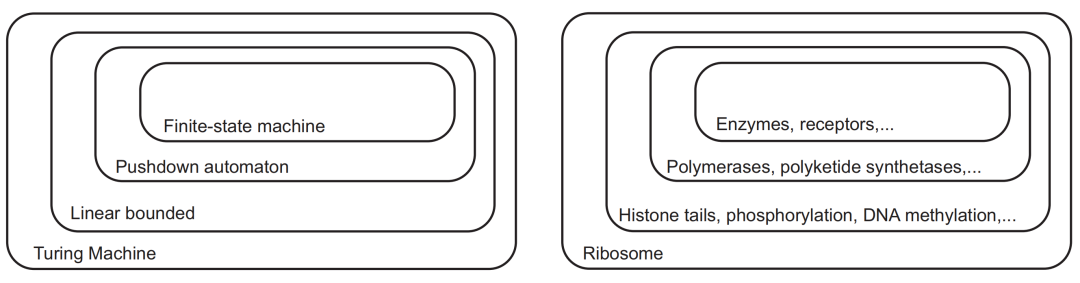
图6. 自动机和生命计算机的不同层级。
在层级结构的底部是“有限状态机”(FSM,finite-state machine),一个将输入转换为输出的转换器(图6)。FSM处理的信息仅存在于其状态和输入中,它没有像图灵机磁带那样的外部存储器。FSM无处不在,从旋转门到洗碗机,自动售货机。冯·诺依曼也使用有限状态机作为工具来阐述他的自我繁殖的抽象模型[4]。虽然看起来像图灵机,但聚合酶在其运动、写入和擦除设备方面受到限制,可以通过FSM模型更好地描述(图5A和B)。细胞中充满了FSM,成千上万的酶和受体将化学底物、机械运动、电或光转化为同样多样化的输出。因为生物分子的行为可以随机地改变,所以它们最好由非确定性的FSM模型来描述,其中给定的输入可以导致具有预定义概率的多个输出。
层级结构中的上一个是“下推”自动机( “pushdown” automata )(图6),机器采用存储设备,在转换期间将符号从“堆栈”中推入或推出。就像我们在自助餐厅看到的一叠托盘一样,操作永远不会在顶部元素之外的元素上工作。生物学中下推机器的例子包括上文没有介绍的DNA聚合酶中的动力学校对(kinetic proofreading)设备。当DNA聚合酶产生复制错误时,不规则的错配被推入规则的沃森-克里克碱基对堆栈中。遵循一组转换规则,DNA聚合酶回溯一个或两个核苷酸,从“堆栈顶部”去除错误掺入的核苷酸。RNA聚合酶在产生RNA时也回溯以检测和响应信号[30]。
再往上的层级是带有图灵磁带的自动机,图灵磁带的长度以某种方式限定(图6),机器可以在其上自由地读写符号。生物分子拥有内置于其结构中的记忆磁带,其残基可以用各种化学取代基进行修饰,以引起更持久的状态变化。例如,在神经细胞的特定蛋白质残基上添加和去除磷酸基团会在大脑中编码长期记忆。添加和删除将DNA结合在一起的组蛋白上尾部突出的化学标记则编码了“表观遗传”指令:这使得有着相同的基于DNA遗传指令的肝细胞和脑细胞具有了不同的身份标记。
图灵机位于这个层级结构的顶端,它可以模拟任何其他计算机(图6)。通过向核糖体提供适当的mRNA磁带,它可以被编程,从而产生出任何生命计算机。确定核糖体和RNA聚合酶是否能够通过蛋白质和RNA来实现通用计算,应该是生物计算的目标之一[31]。
7
解码生命计算
在证明判定问题无解的过程中,图灵表明,无论多么强大的计算机程序,都无法预测另一个程序的命运。用冯·诺依曼的话来说就是“你无法构建一个能预测任意自动机行为的自动机”。斯蒂芬·沃尔夫勒姆(Stephen Wolfram)通过他的“计算不可约性”(computational irreducibility)原则阐述了这一观点,该原则指出,一旦计算达到一定的复杂程度,就不能再走捷径来理解计算的结果——完全理解输出的唯一方法是完全运行程序[32]。而运行这个程序正是大自然在过去38亿年的进化中一直在进行的实验。每一个子代都运行一个新的程序,通过反复试错,演化战胜了判定问题。而这个过程必须付出的代价则是基因组并不与我们同在,我们只看到了所有存在过的生物程序中极小的部分。
假设生物体是复杂计算的产物。在这种情况下,不可能通过测量生物化学过程的输入和输出来理解和计算生物体的行为,也不可能走捷径来发现它们之间的关系;这种方法肯定会失败。然而,由于人类基因组测序和人工智能带来的技术革命,这种“大数据”科学模式正在渗透到生物学的许多领域。用西德尼·布伦纳(Sydney Brenner)的话来说,结果是我们“淹没在数据的海洋中,但仍然渴望知识”。
知识要求我们将细胞内的每个生物分子还原成适当的转换表,然后完整地运行程序。我们预计生物分子采用少量的转换规则,这些规则可以以各种组合编织在一起,来构建活生物体中的所有生化过程。这类似于系统生物学发现的相对较小的网络模体(motif),它们似乎是转录网络的基本生物砖[20]。确定转换规则应该是生物计算领域的目标之一。
知识还要求我们理解如何基于生物分子的序列和物理定律来实施转换规则,这些规则决定了生物分子的构象行为以及它如何与周围环境相互作用。从序列中预测转换规则应该是目标,而不是主导结构,这是最近人工智能工作的重点[33]。有了适当的转换表,我们可以更有效地将结构生物学与系统生物学结合起来,更好地计算细胞和整个生物体的行为,并合理地对生物学进行重新编程,以满足技术、健康和社会需求。
通过将生物学简化为计算形式,计算机科学这整个领域都可以被用来将生物学系统化。例如,计算复杂性领域可用于研究各种生化反应中时间、内存和能量之间的权衡,并分类和探索生物计算需要解决的多样性问题。同时,计算机科学家可能能够挖掘生命计算中的自然宇宙,利用数十亿年来的演化来发现新的计算模型或算法,甚至可能回答数学和逻辑方面的问题。毕竟,神经元的行为建模正是神经科学家Warren McCulloch和逻辑学家Walter Pitts开发人工神经网络的灵感来源,为人工智能奠定了基础[34]。生物体如何利用量子力学[35]还可以为建造下一代量子计算机提供重要线索。
展望未来,我们可能会发现生物学和计算机科学是紧密相连的,它们是同一门学科,一门研究机器行为的学科。
注释:本文在翻译 biological computation 时做了区分,认为“生物计算”和“生命计算”是不同的概念。生命计算强调以生命系统为蓝本的、计算的整体设计,而生物计算强调具体的以DNA、蛋白质大分子等为元件,它的原理可以和生命系统没有关系,而单纯使用计算机原理或简单数学原理。
参考文献
[1] A. Bhattacharya, The Man From the Future (Norton, 2022).
[2] N. Wiener, Cybernetics or Control and Communication in the Animal and the Machine (Hermann & Cie/The Technology Press/John Wiley & Sons, 1948).
[3] L. A. Jeffress, Cerebral Mechanisms in Behavior: The Hixon Symposium (Wiley, 1951), p. 311.
[4] J. V. Neumann, Theory of Self-Reproducing Automata, A. W. Burks, Ed. (University of Illinois Press, 1966).
[5] A. M. Turing, On computable numbers, with an application to the Entscheidungs problem. Proc. Lond. Math. Soc. 42, 230–265 (1936).
[6] K. Gödel, Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik 38, 173–198 (1931).
[7] F. Crick, Central dogma of molecular biology. Nature 227, 561–563 (1970).
[8] J. D. Watson, F. H. Crick, Molecular structure of nucleic acids; a structure for deoxyribose nucleic acid. Nature 171, 737–738 (1953).
[9] L. Pauling, R. B. Corey, A proposed structure for the nucleic acids. Proc. Natl. Acad. Sci. U.S.A. 39, 84–97 (1953).
[10] S. Brenner, Interview with Sydney Brenner by Soraya de Chadarevian. Stud. Hist. Philos. Biol. Biomed. Sci. 40, 65–71 (2009).
[11] S. Brenner, Turing centenary: Life’s code script. Nature 482, 461 (2012).
[12] F. Jacob, J. Monod, Genetic regulatory mechanisms in the synthesis of proteins. J. Mol. Biol. 3, 318–356 (1961).
[13] C. H. Bennett, Logical reversibility of computation. IBM J. Res. Dev. 17, 525–532 (1973).
[14] L. M. Adleman, Molecular computation of solutions to combinatorial problems. Science 266, 1021–1024 (1994).
[15] Q. Liu et al., DNA computing on surfaces. Nature 403, 175–179 (2000).
[16] D. Faulhammer, A. R. Cukras, R. J. Lipton, L. F. Landweber, Molecular computation: RNA solutions to chess problems. Proc. Natl. Acad. Sci. U.S.A. 97, 1385–1389 (2000).
[17] Y. Benenson, Biomolecular computing systems: Principles, progress and potential. Nat. Rev. Genet. 13, 455–468 (2012).
[18] D. Murray, D. Petrey, B. Honig, Integrating 3D structural information into systems biology. J. Biol. Chem. 296, 100562 (2021).
[19] H. V. Westerhoff, B. O. Palsson, The evolution of molecular biology into systems biology. Nat. Biotechnol. 22, 1249–1252 (2004).
[20] U. Alon, Network motifs: Theory and experimental approaches. Nat. Rev. Genet. 8, 450–461 (2007).
[21] A. M. Turing, The chemical basis of morphogenesis. 1953. Proc. R. Soc. Lond. B Biol. Sci. 237, 37–72 (1952).
[22] H. Frauenfelder, S. G. Sligar, P. G. Wolynes, The energy landscapes and motions of proteins. Science 254, 1598–1603 (1991).
[23] S. S. Patel, I. Wong, K. A. Johnson, Pre-steady-state kinetic analysis of processive DNA replication including complete characterization of an exonuclease-deficient mutant. Biochemistry 30, 511–525 (1991).
[24] M. E. Dahlberg, S. J. Benkovic, Kinetic mechanism of DNA polymerase I (Klenow fragment): Identification of a second conformational change and evaluation of the internal equilibrium constant. Biochemistry 30, 4835–4843 (1991).
[25] R. D. Kuchta, V. Mizrahi, P. A. Benkovic, K. A. Johnson, S. J. Benkovic, Kinetic mechanism of DNA polymerase I (Klenow). Biochemistry 26, 8410–8417 (1987).
[26] D. E. Koshland, Application of a theory of enzyme specificity to protein synthesis. Proc. Natl. Acad. Sci. U.S.A. 44, 98–104 (1958).
[27] J. D. Watson, F. H. Crick, Genetical implications of the structure of deoxyribonucleic acid. Nature 171, 964–967 (1953).
[28] I. J. Kimsey et al., Dynamic basis for dG*dT misincorporation via tautomerization and ionization. Nature 554, 195–201 (2018).
[29] J. J. Hopfield, Kinetic proofreading: A new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc. Natl. Acad. Sci. U.S.A. 71, 4135–4139 (1974).
[30] E. Nudler, RNA polymerase backtracking in gene regulation and genome instability. Cell 149, 1438–1445 (2012).
[31] H. Akhlaghpour, An RNA-based theory of natural universal computation. J. Theor. Biol. 537, 110984 (2022).
[32] S. Wolfram, A New Kind of Science (Wolfram Media, Champaign, IL, 2002).
[33] J. Jumper et al., Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021).
[34] W. S. McCulloch, W., Pitts, A logical calculus of ideas immanent in nervous activity. Bull. Math. Biophys. 52, 99–115 (1943).
[35] J. McFadden, J. Al-Khalili, The origins of quantum biology. Proc. Math. Phys. Eng. Sci. 474, 20180674 (2018).
本文经授权转载自微信公众号“集智俱乐部”。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 