量子计算的重要理论问题：如何给通用模型分类？-返朴的财新博客-财新网

给通用量子计算模型分类是当前量子计算理论领域重要的问题，因为很多通用模型是在不同时期、由不同背景的研究人员提出，缺乏对它们系统的研究。如何严格地定义一个模型？如何统一地描述通用模型？本文作者团队近期刊发论文，从量子资源理论出发，发展了通用量子计算模型的分类理论，并提出了包括冯·诺依曼架构在内的一些新的计算模型。

撰文 | 王东升（中国科学院理论物理研究所）

01摘要

量子计算领域主要研究量子信息的性质及其应用。在各种量子信息技术迈向实际应用的背后，这一研究领域的基础理论尚不完善。我们近期在《理论物理通讯》发表论文，系统研究了通用量子计算模型，提出了一套用于其定义、分类、核心资源刻画等的理论，并提出了量子冯·诺依曼架构这一类新模型。此研究不仅发展了通用量子计算理论，还揭示这一领域尚有很多深刻的基本问题去发掘。

02引言

量子计算领域有几种不同的叫法，比如早期将量子信息与量子计算并称，后来也叫量子信息科学。不管是什么名称，它研究的基本内容是量子信息及其演化规律。其发端与经典的计算领域不无联系。在上世纪80年代，物理学泰斗费曼在经过对量子电动力学的研究和经历了曼哈顿计划之后，对计算机产生了兴趣，因为研究当中涉及到了大量的计算问题。费曼等人意识到[1]，用可控的量子系统去模拟未知的量子现象，应该比用非量子的所谓经典计算机要更高效，比如去计算描述粒子碰撞的费曼图，见图1。这其实是很超前的理念，当然这其中不乏另一位天才冯·诺依曼的启发。因为在那个时期，基于冯·诺依曼的理论，经典计算机也正越来越引起人们的关注。经过半个多世纪的发展，经典的信息和计算领域取得了巨大进步，造就了当今所谓的信息时代。

量子计算领域也逐渐发展壮大，分化出量子通讯、量子算法、量子模拟、精密测量等方面，展现出巨大的潜力。比如，采用著名的肖尔（Shor）算法可以高效地破译一些经典密码。在很多方面比如线性代数问题中，量子算法可以指数级地降低计算资源。物理学家们更为期待的是实现费曼的设想，即用量子计算机实现对量子系统的高效模拟。近期，领域内几位在理论和实验方面的奠基人分别获得了诺贝尔物理学奖和基础物理学突破奖，是对这一领域的极大鼓舞。

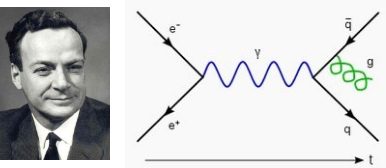图1：费曼（左）和一个费曼图（右）

然而，建造量子计算机远比想象的要困难很多。其基本原因是作为量子信息基本载体的量子比特的状态非常不稳定，其量子特性很容易在环境的扰动下退化，即产生退相干（decoherence）。更进一步，为了实现各种计算任务，一般需要实现对多量子比特的高精度操控，来制备各种所谓的量子纠缠态，而这也是同样困难的。目前，较为成熟的实验平台包括光子、超导、离子阱、冷原子等，物理学家可以实现对上百个量子比特的操控。然而，大多数平台离不开极低温或高真空环境，且量子比特的寿命很短。相比之下，基于磁盘、晶体管、光盘等的经典比特不仅可以在常温下稳定存储很久，其操控频率也就是我们日常使用的电脑的主频（一秒内可以执行的操作数）已经达到了~GHz量级。

随着研究领域范围的不断拓展，量子计算也面临一些发展中积累的问题。一是研究呈现出分化的态势，即不同的研究方向越来越远。这是专业分工的自然结果，但这也导致研究结果分散，不易互相借鉴和融合。更为重要的是，领域内有很多“不可能定理”，比如不可克隆定理等，这一方面区分了量子信息与经典信息，一方面也给人们的认识带来一些困扰。（试想，不可克隆的量子信息如何实现下载上传、复制粘贴等这些基本操作？）因而，为了取得长足的进步，有必要从整体着眼，将不同的研究进展统筹并结合起来，进而去深化对基本问题的认识，这也是我们所采取的研究思路。

03通用计算模型

我们讨论的起点是计算模型，常用的经典计算模型有线路模型、图灵机、元胞自动机等。之所以有不同的模型，是因为它们的出发点不同，也有不同的应用，更重要的是它们是各种算法的基础。这些模型还是很好用常识来理解的，比如，在交通领域中，车辆在红绿灯的指引下有序运行时类似于线路模型，车辆的先后顺序会受到红绿灯的调控；而在一条狭窄的路上，即使没有红绿灯，相对而行的自行车一般也会自动形成两个车流，这更类似于元胞自动机；当交通发生堵塞时，则更需要一个强有力的指挥来与每一辆车交流，进而疏散交通，这类似于图灵机的工作方式。

值得注意的是，这些模型都是“通用模型”。这是由计算机学家定义的概念，对物理学家可能有点陌生。在物理学中也有很多模型，但基本都不是通用的。比如，常用的Ising模型可以用来描述铁磁系统，但它与比如sine-Gordon模型、Hubbard模型等则不同，它们描述的是不同的物理现象。而通用计算模型之间是等价的。通用性（universality）是指用模型中所允许的对象和操作能够有效地实现任意的过程。其等价性要求对于给定的过程，两种不同的实现方式之间可以互相模拟。例如，不管如何指挥交通，其目的都是为了实现畅通的车流。计算模型的背后其实是基本的物理学定律，涉及到物体的运动在时间、空间、或能量等方面的约束条件。因而，我们可以用理论物理的语言来研究通用计算模型。

在量子计算中，最常用的是量子线路模型，它与经典情况类似（大学计算机基础课里学的布尔逻辑线路），是指用量子逻辑门作用在量子比特上，最后用测量来读取结果。它要求对每个量子比特的精准控制以及至少两两之间的控制。除此之外，由于量子过程的复杂性，人们建立了更多的通用模型，这一点远比经典情况更为丰富。比如，量子测量可以改变量子比特状态，这与经典测量非常不同。一种通用模型即基于量子测量，即给定某类所谓的“图态”（graph states），然后通过一系列关联的单比特测量来实现量子计算[2]。这一模型被某些光学量子计算公司所采用[3]。还有一些模型并未得到充分研究。比如，图灵机模型在经典计算理论中非常重要，然而，在量子计算领域中对它的研究则比较少[4]。其原因一方面是因为量子线路模型太过流行，一方面是因为量子图灵机模型本身比较复杂，人们不太清楚如何应用。在领域内，很多通用模型是在不同时期、由不同背景的研究人员提出，人们对它们的研究是比较分化的，应用的侧重点也不同，缺乏对它们系统的研究。那么，更一般地，人们会问：如何严格地定义一个模型？是否能对不同的模型进行分类？在未来是否还会有更多的模型？等等。我们发现这些问题是可以回答的。

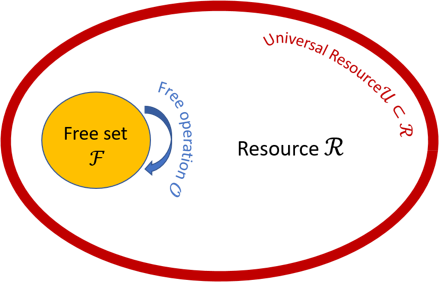
图2：量子通用资源理论的结构示意

04研究问题：如何统一地描述通用模型

为了统一地描述通用量子计算模型，我们需要找到合适的分类理论。在物理学中，常用的分类理论是群论，用于描述系统的对称性。然而，计算过程一般不涉及特定的对称性。我们发现，量子资源（resource）理论[5]是更合适的理论。量子资源理论用于描述各种量子特性，其确立也只是近几年的事。量子资源理论的起点是集合论。给定某个集合，选定其某子集，以及操作集使得。剩下的部分被称为资源集，而子集则相应地是一种限定集。

最简单的量子资源的例子是由熵来刻画。我们知道，经典信息是由香农熵来定义，它是一个概率分布的函数。相应地，量子信息可由冯·诺依曼熵来定义，它是霍列沃（A. Holevo）等人在上世纪70年代所采用的方法[6]。量子态也可以看作是一个算符，其本征值构成一个概率分布，其香农熵即是此量子态的冯·诺依曼熵。一个量子态所包含的信息量即资源度，是由（负）熵来度量的：完全混合态的信息量为零，而纯态的信息量最大。另外一个有名的例子是量子纠缠。不纠缠的态被称为可分态，其余的都是纠缠态，其纠缠度即为其资源度。我们所熟知的Cooper对和Bell态，都是两体最大纠缠态的例子。除此之外，量子相干性也是一种资源。对于量子态的集合，选定希尔伯特空间的一组基，那么在这组基下对角形式的态被称为经典态即非相干态，其资源度为零，剩余的态是相干的叠加态。如果选定所谓的稳定子态（stabilizer）作为限定集，则剩余的态是所谓的magic的“幻态”。通过这些例子，我们其实也认识到，量子信息的资源度不仅仅需要熵来刻画，也需要更多的量来全面地反映其性质。

量子资源理论主要用于对量子信息性质的刻画上，但在量子纠错、计算模型等更偏量子计算过程上的应用则比较少。为了研究通用模型，我们首先将资源理论的框架做进一步扩充。如图2所示，定义资源集中资源度最大的部分作为通用集，使得过程可以有效模拟任意的过程。更进一步，我们定义子集链F1 ⊇ F2 ⊇ F3...，则相应地 R1 ⊆ R2 ⊆ R3...。为了实现通用性，需有如下计算性能上的关系U1 < U2 < U3...。一个通用模型即用来实现任意的量子演化或算法，其中的可以代表其算法优势的来源。采用不同的集合，可以定义不同的“家族”（family），然后采用子集的链式结构，则可以定义家族中的“代”（generation），即不同的计算模型

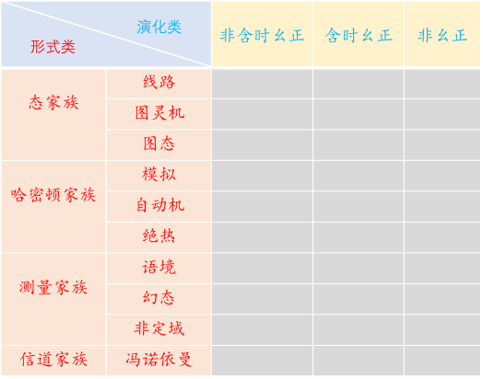
图3：通用量子计算模型分类示意表格

基于如上基本思路，我们初步发展了量子计算模型的分类理论[7]。首先，我们从三个方面来分析一个计算过程：信息的表示形式、信息的保护、信息的演化。这三者其实构成了信息的三个维度，其表示形式是指信息以何种方式存在，保护是指采用何种编码方式来对抗噪声，演化是指用何种类型的逻辑门来实现信息的处理。其中保护更多地涉及到编码模型，这里不做讨论。针对另外两个方面，可以定义两类计算模型，见图3中表格示例。我们详细研究了针对信息的存在形式的模型分类（红色部分）。在量子理论中，我们可以把信息编码到量子态、哈密顿、测量过程或量子信道中，针对这四种信息的存在形式，我们分别定义4个家族，每个家族有3代。例如，态的家族包括线路模型、定域图灵机模型和基于图态的模型（通常称为“One way”模型[2]），其操作集是越来越受限的，从任意的非相干经典操作到定域操作（所谓LOCC）再到单点（on-site）操作。它们所需的资源也不同，分别为相干性、纠缠和对称性保护的纠缠[8]，其相应的计算能力也是越来越强的。这是符合我们的直觉的：为了达到同样的目的，如果给定的条件越有限，那么需要的额外算力就越高。这也适用于其他家族。其中，哈密顿家族包含了费曼所构想的量子模拟，测量家族包含了基于幻态的模型。由于篇幅有限，我们不一一介绍了。基于信道的家族是我们提出的一类新的模型，可以统称为量子冯·诺依曼架构，我们稍后详细介绍。

另外，我们也初步研究了针对信息演化（即量子逻辑门）的模型分类（图3中蓝色部分）。我们划分了3个家族，分别对应非含时幺正逻辑门、含时幺正逻辑门以及非幺正逻辑门。对于第一种，又可以根据逻辑门的深度（depth）区分出3代，分别对应Depth-1, Finite-Depth, 和High-Depth的模型。注意，这里考虑的是基本的逻辑门，例如H，T，CNOT，而任意的逻辑门可以表示为它们的一个序列。其中，High-Depth模型可以描述拓扑量子计算[9]，其逻辑门需要用非阿贝尔的任意子的编织操作来实现，它们的逻辑深度是线性的。Depth-1模型可以描述量子精密测量：一未知过程通常对应于depth-1的全局操作，将其作用于某资源态上，然后测量。由于量子不确定性原理，其所估计值的精度是有限的。

如果将这些模型放在同一个表格中，以信息的演化作为横轴，信息的形式为纵轴，那么可以考虑如何将它们互相结合起来以填满整个表格（图3），这将产生上百种不同的计算模型或方案。这有点类似于门德列夫的化学元素周期表，或者是拓扑物态中的Kitaev的表格或更完备的分类表格[10]，但也不尽相同。我们发现，表格中有一些方案已经得到了研究，而另一些则没有，这是值得更多探索的内容。

图4：冯·诺伊曼和其计算机架构原理示意图05量子冯·诺伊曼架构

最后，我们介绍一下前面提到的量子冯·诺依曼架构。在计算机的发展中，图灵首先建立了计算理论，而冯·诺依曼更进一步，发展了计算机架构理论，为电子计算机的建造奠定了理论基础。注意，人们一般将其称为一种“架构”而不是模型，但都是指我们所说的通用模型。在此架构下，计算机可以分解为CPU、存储、控制、通讯等模块。其中，算法也可以被存储为数据，在控制器的调控下，算法本身可以被读取、运行。因而，不需要改变芯片的结构就可以实现不同的算法。见图4。在理论上，这其实是可编程性（programmability）对通用性的补充。虽然布尔代数可以保证通用性，但是它不能保证同一个芯片可以执行很多不同的算法。

那么，量子计算机是否可以采用冯·诺依曼架构？这个问题其实很早就得到了研究。在1997年，M. Nielsen和I. Chuang研究了量子可编程性，但得到了否定的回答，通常称为量子不可能编程定理。即如果，那么不同的程序对应的程序态需要完全可区分，即是经典的数据。试想，对于一个量子比特上的旋转操作，不同的角度需要存储为完全可区分的量子态，那么这与经典存储并无区别。这一不可能定理很大程度上决定了当前量子计算的研究现状：即人们大都在努力实现量子的CPU，而不是完整的基于冯·诺依曼架构的量子计算机。

基于近期的发展特别是测量计算模型和量子超信道理论，我们提出了量子冯·诺依曼架构[11]。首先，任意的量子过程或程序可以表示为一个信道（channel）。基于信道-态对偶原理（channel-state duality），我们用它的对偶态做为存储的程序态。这一对偶原理可以保证在程序态上的观测等价于原信道所能产生的观测效应。采用这一方案可以绕过不可编程定理。与提取在输入态上的作用不同，我们只要求提取在末态上的观测效果，即保证得到所需力学量的期望值，毕竟这是算法的最终读取结果。同时，还需要保证程序的可组合性，即把不同的程序组合为一个新的程序，这一点我们用一个扩展的量子隐形传态机制来实现。加上量子的控制单元和量子通讯，则构成量子冯·诺依曼架构，其逻辑结构如图5所示。量子程序态是二分的结构，因而表示为弯曲的弧形。另外，我们简要指出它与量子资源理论的关系。选取集合为信道的对偶态集合，根据不同的操作定域性可以定义子集链，那么相应地，实现通用性所需要的程序态的类型则不同。

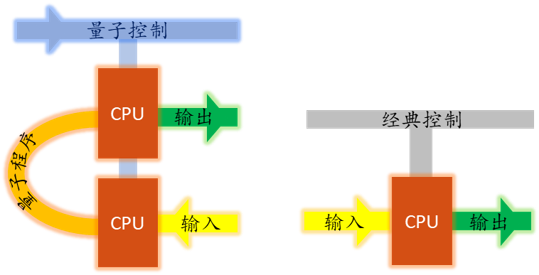图5：冯·诺伊曼架构（左）与线路模型（右）

在常用的线路模型（图5右）中，控制和程序都是经典的，初始数据态作为输入是提前制备好的。在量子冯·诺依曼架构（图5左）中，初始数据态是通过测量的方式“写入”的，而不是提前制备好。量子的程序是需要提前制备和保存好的，由于其量子特性，它们不能被任意地克隆。换句话说，量子的程序具有保密性，这一点也是量子通讯的一大特性。信息的发送方可以实现将数据发送给接收方使用，同时不泄露数据本身给接收方或者窃听者。另一方面，一系列对程序态上的操作实质上构成一个“超信道”[12]，这其中也包括量子控制单元的作用。从算法的角度来看，如果程序本身是在一个算法的层次上，那么作用在其上的超信道实则构成一种“超算法”，它可以实现从一个算法到另一个算法的转变。机器学习算法就是一种超算法[13]，它是在给定一个问题之后，预先没有相应的算法，而是在对大量的先验数据进行学习之后形成一个算法，继而去解决问题。我们发现，量子冯·诺依曼架构就非常适用于执行这类超算法。

06结论

我们从量子资源理论出发，发展了通用量子计算模型的分类理论，并提出了包括冯·诺依曼架构在内的一些新的计算模型。更进一步，模型之间的对比甚至结合也是有益的。在实践中，某种模型可能更适用于特定的物理系统或设计特定类型的算法，满足更多的要求，比如模块化、可编程化等。我们的研究对领域内其他的研究方向也有一定的参考意义。在物理实验方面，目前人们一般更关注量子芯片（CPU）的制造和量子通讯，而对如何建造完整的量子计算机，特别是如何实现量子的存储和控制单元关注较少。在算法方面，是否可以从量子资源的角度来认识算法的优势，甚至直接定义量子的计算复杂度也是值得探索的。总之，相比于经典计算机的发展，量子计算领域的发展尚不成熟，在理论、技术、应用等各个方面都还有很大的发展空间。经典计算与信息领域有一部生动的演化史[14]。对于量子领域来讲，我们相信也会如此。