图片由董彬老师用DALL-E生成

撰文 | 高国雄、姜杰东、董彬

八年前，横空出世的AlphaGo横扫围棋赛场，点燃了人工智能的热潮，也从根本上改变了围棋领域。近日，谷歌Deepmind团队一篇瞄准国际奥林匹克竞赛（IMO）几何题目的论文“AlphaGeometry”[1]再度一石激起千层浪。国内外对此已有铺天盖地的报道与讨论，诸如“解决前沿数学问题指日可待”“奥赛金牌近在咫尺”等评价将大众对人工智能解数学题的期许推上了新的高峰。本文将深度解读AlphaGeometry，简要分析其与之前最好的基准模型的差距，并对该模型的发展前景给予评述。

01

模型概述
 

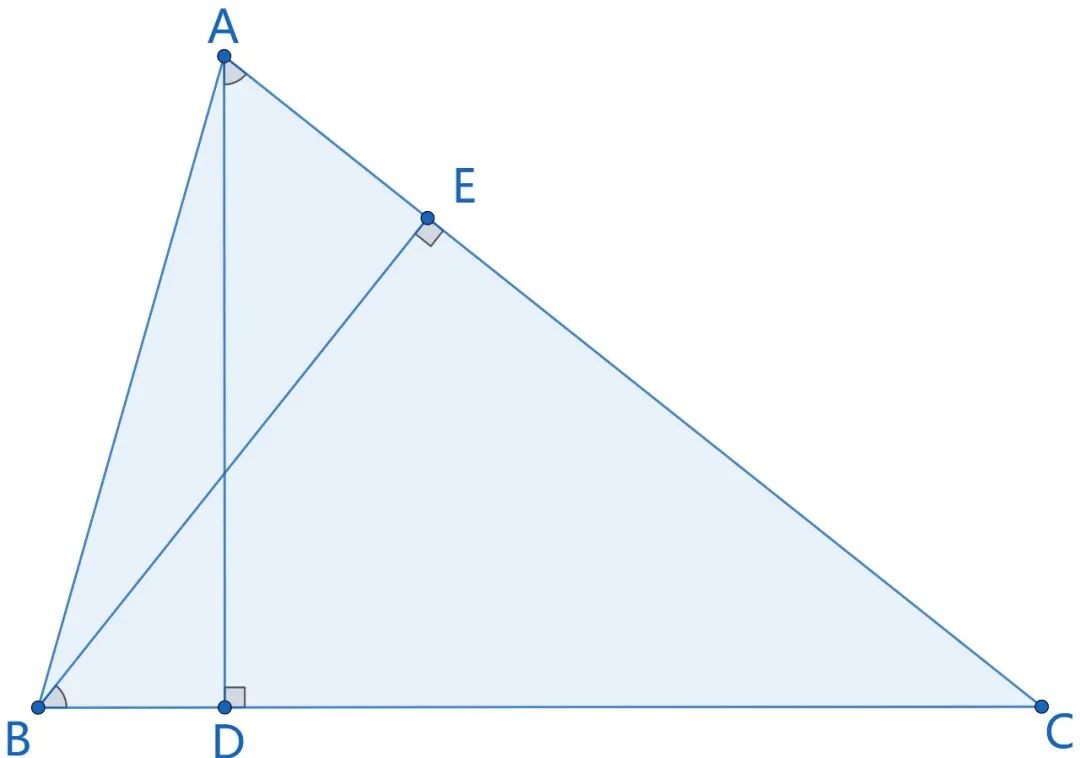
图1

欧氏几何题目因其规范的叙述和标准化的解题流程，是各类国内国际数学竞赛的“常客”。平面几何相比其他数学领域所具有的封闭性、简洁性、可验证性，也让它更适合机器证明。上世纪七十年代，吴文俊院士提出的“吴方法”[2]是这一领域的奠基之作，而随后涌现的推理数据库 (deductive database，简记为DD) 方法[3, 4]则在保留证明的有效性的同时，大大提升了证明的可解释性。

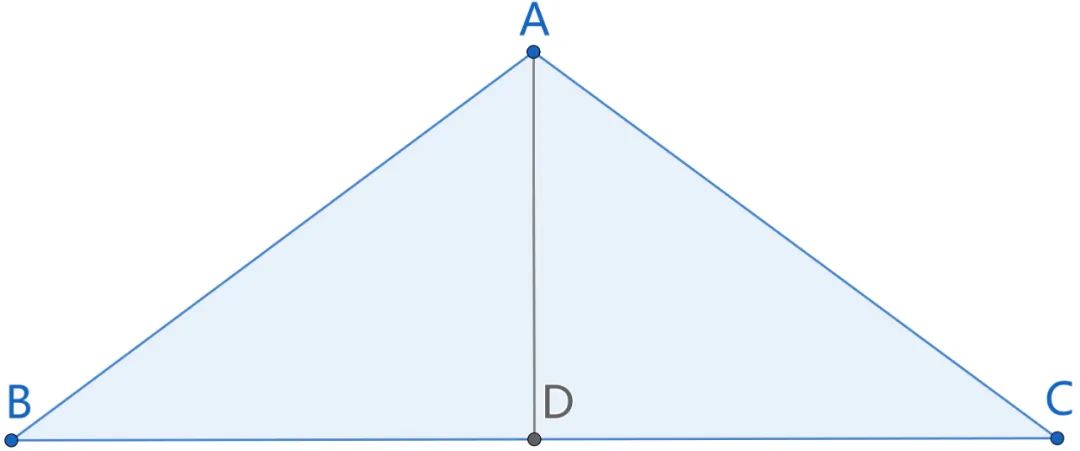
图2

以文献[3]为例，DD的核心是一系列包括共线、平行、中点、共圆、等角、等比等欧氏几何基本要素的共七十五条的推理规则。在给定的图形中，DD系统可以从给定前提（premises）出发，反复应用这些推理规则，不断得到新的结论，直到所有可能得到的结论都被穷尽。此时所有生成的定理按其推理路径组成一个有向无环图，这被称为在给定图形中指定前提的推理闭包（deduction closure）。此时，如果待证的结论就在推理闭包中，回溯证明路径就得到一个合规的证明。在图1中，以BE⊥AC，AD⊥BC为前提，往证∠EBC=∠DAC，DD在搜索中很容易通过BE⊥AC,AD⊥BC⇒∠ADB=∠AEB⇒AEDB共圆⇒∠EBC=∠DAC的路径得到结论。

然而，DD并不能在现有的图形基础上添加任何辅助点，这大大限制了DD的表达能力。在图2中，对△ABC，以AB=AC作为前提，除非添加一个辅助点，如AB中点D，否则DD系统无法在推理闭包中得到∠ABC=∠ACB的结论。即便是如此简单的初中几何题目也超出了DD的能力范畴，因此，添加辅助点的能力对几何推理系统的重要性不言自明。对于高难度的平面几何竞赛题目来说，光靠DD这种遍历搜索的方法，而不依赖辅助点的添加，是不可能取得好成绩的。

在AlphaGeometry这篇工作中，作者还在DD的基础上，额外使用了用于处理角、边的相加和比例关系的线性代数规则系统 (algebraic rules，简记为AR) 以补充DD的推理能力的不足。后面我们把DD和AR联合的推断系统记为DD+AR。

尽管DD+AR已有较强的推理能力，但还是无法解决添加辅助点的问题。在过去的研究中，人们就已经设计了启发式的（heuristic）策略来添加辅助点以拓展DD和AR的搜索空间。AlphaGeometry在自己构建的30道IMO题目上测试DD+AR+heuristic，可以做对其中的18道题。在这个基础上，AlphaGeometry的主要贡献是训练了一个151M大小的语言模型来代替启发式算法，以实现更好的加辅助点策略，获得了从做对18道题目到25道题目的进步。

为训练这一语言模型，作者首先利用已有的DD+AR框架合成了大量数据。添加辅助点被限定在约五十条规则组成的框架内。通过反复进行“运行DD+AR生成定理闭包→随机添加辅助点”的循环，我们可以得到一个足够复杂的有向无环推理依赖图，每个节点均为一个结论，每条边为所调用的推理规则。对任意一个结论进行反向回溯搜索其最小生成树，可以得到“<所用前提>，<所得结论>，<证明路径>”的三元组，这就是用于训练语言模型的一个数据。在调用100,000个CPU线程并行运算72小时后，作者得以生成约5亿个数据，排除重复后剩余约1亿个，其中约900万个包含“添加辅助点”的步骤。最终使用的语言模型为先在这1亿个数据上预训练，再在这900万个含添加辅助点步骤的数据上微调得到。

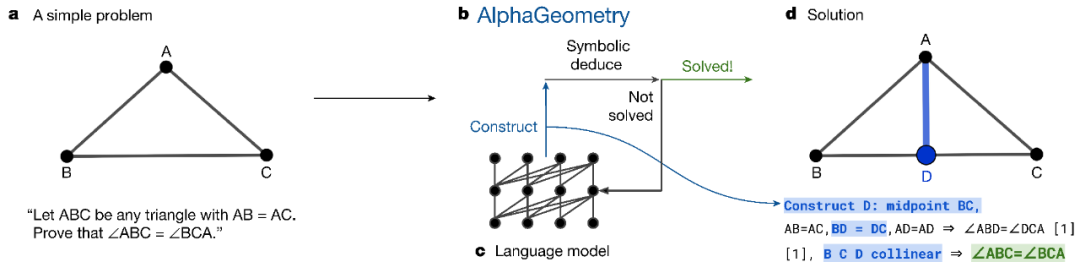
图3

在解决实际几何问题时，AlphaGeometry以给定的前提和基础图作为根节点和初始筛选节点，在每轮中先对当前全部进行筛选的节点运行DD+AR以生成推理闭包。如果此时往证结论仍未出现，则在所有筛选节点的所有可能加辅助点的方案中，选取在语言模型中生成概率最高的512个作为下一轮的筛选集合。循环将持续进行，直到筛选轮数达到设定的搜索深度或往证结论在某个推理闭包中出现时终止。

如图3所示，通过反复交替调用DD+AR和语言模型，让二者分别专注于几何推理和辅助点构造，AlphaGeometry得以解决多数IMO几何题目。按论文作者估算，在1.5小时限时（这是IMO竞赛中每道题的平均限时）下，提供四个并行的V100加速的语言模型和76个CPU线程就足以解决AlphaGeometry能解决的25道题目中的24道。这证明了AlphaGeometry构架的有效性。

02

评价

总的来说，AlphaGeometry能解决所选的共30题的IMO题集中的25道，已经展现了其在几何推理上的有效性。下面，我们从两个方面对AlphaGeometry的能力和潜力进行评价。

1．DD+AR系统的局限性

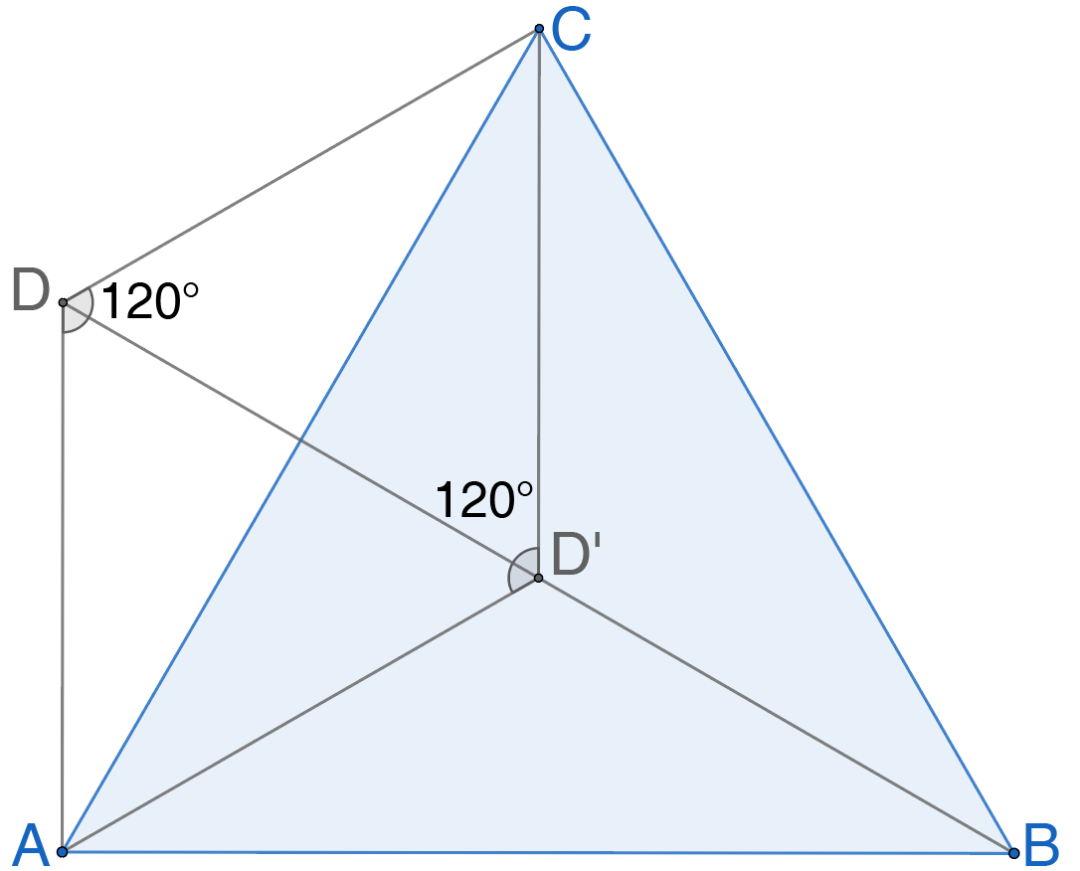
图4

AlphaGeometry高度依赖DD+AR系统，其精心训练的语言模型要和DD+AR的体系配合。因此，AlphaGeometry的能力也被DD+AR系统的表达能力所局限。

如图4所示，设D是正△ABC外一点，满足DB⊥AC且∠ADC=120°。往证DA⊥AB。这是一道容易通过简单的角度计算给出证明的题目。然而，这只对D落在△ABC外的情形成立！如果失去了“设D是正△ABC外一点”这一描述位置关系的条件，便无法区分图中D，D’两点。即使所有其他前提叙述都不改变，结论也不再成立。DD+AR系统所使用的语言无法描述“D在△ABC外”这一相对位置关系，无论添加多少辅助点都无济于事。这种对位置关系的依赖在IMO等级的题目中通过精巧的设计与规范得以尽量避免，却在欧氏几何所囊括的定理中广泛存在。甚至在许多不追求规范性的题目中，题干根本不使用文字叙述点明位置关系，仅仅叙述“如图”二字而已。另外，DD+AR体系的推理，在所有取点互异的暗含前提下才是可靠的（例如DD中有一条规则是若ABC共线且ABD共线则CDA共线，这一论断在AB重合时不成立）。

即便不考虑组合几何和几何不等式，以上两种情况在所有值得考虑的平面几何定理中占比约30%。进而，DD+AR+LM（语言模型）的组合也只能支持考虑约70%的几何题目。因此，DD+AR系统限制了AlphaGeometry的可拓展性。

2. 所训练的语言模型带来的实际增益

想要客观分析语言模型带来的增益，我们应当将AlphaGeometry (DD+AR+LM) 与DD+AR+heuristics（启发式添辅助点）相比较。在考虑为训练LM所耗费的庞大算力资源和一亿的数据量后，前者解决25/30道题目的成绩相比后者18/30道的增益并不足够显著。

必须指出，虽然AlphaGeometry同属“Alpha”家族，但与AlphaGo不同，它并非利用强化学习维护一个高效的策略（policy），而是使用纯粹的监督学习。这也意味着，模型并不会利用其在部署后进行推断时的搜索的正确与否来不断修正自己的权重。不过，想要将现有的监督模型改造为强化学习模型，DD+AR框架的高延迟（每次生成推理闭包需要几秒到几分钟）是营造强化学习所需的即时大量反馈的环境的一大阻碍。

另一方面，考虑到在搜索深度（即调用语言模型来添加辅助点的次数）为4和2时，模型仍有能做出25道和21道的表现，可见想实现优秀的推理能力，并不需要很高的搜索深度。这表明在AlphaGeometry中，对分析、搜索推理空间的贡献更多集中在DD+AR，而非所训练的语言模型。

03

总结

AlphaGeometry给出了一个能够解决IMO难度的平面几何题目的有效架构。然而，受限于DD+AR的表示能力，想要将这篇工作的架构拓展到标准平面几何剩下的约30%题目十分困难。同时，DD+AR充分利用了平面几何简洁明确的推理结构，但也因此被局限在几何的范畴内，难以拓展到数学其他领域。不过，利用DD+AR提供的回溯功能，我们可以对已证明的定理给出多种不同的回溯路径，也就给出同一个结论的不同证明方法。这能否对学生学习几何证明给予有效的指导，有待进一步考证。

正如论文所提到的，这篇工作所着手的对象范围较为狭窄，其核心原因在于形式化数据的不足。以Lean为代表的一系列形式化数学语言为自动定理证明提供了逻辑严密、表达能力强且能自动验证的交互环境，这是解决类似于DD+AR这样的小领域符号引擎的表达能力限制的突破口。只有联合Lean community等形式化社群进行更全面、广泛的形式化数学数据的积累和收集，AI4Math才能有本质上的进展。

文献

[1] Trinh, T.H., Wu, Y., Le, Q.V. et al. Solving olympiad geometry without human demonstrations. Nature 625, 476–482 (2024). https://doi.org/10.1038/s41586-023-06747-5

[2] Wu, W.-T. On the decision problem and the mechanization of theorem-proving in elementary geometry. Sci. Sin. 21, 159–172 (1978)

[3] Chou, S. C., Gao, X. S. & Zhang, J. Z. A deductive database approach to automated geometry theorem proving and discovering. J. Autom. Reason. 25, 219–246 (2000)

[4] Ye, Z., Chou, S. C. & Gao, X. S. in Proc. Automated Deduction in Geometry: 7th International Workshop, ADG 2008 (eds Sturm, T. & Zengler, C.) 189–195 (Springer, 2011). geometry. Sci. Sin. 21, 159–172 (1978).

本文经授权转载自微信公众号“北京国际数学研究中心BICMR”，原标题为《简评DeepMind新作AlphaGeometry》。