希格斯机制是一个用于解释基本粒子质量起源的物理机制。文章介绍了希格斯机制的基本概念，并运用多项式函数等初等数学知识阐释了希格斯机制和自发对称性破缺的物理内涵，最后评述了对称性思想在现代科学发展中的重要意义。

撰文 | 朱宏伟（清华大学材料学院）

2023年8月，美国费米国家实验室的“µ子g-2实验”团队宣布了µ子磁矩的最新实验结果，将实验值与理论预测值的偏差置信度提升至5个标准差，这表明存在物理新发现的可能性高达99.99994%。

早在2021年4月，费米国家实验室就曾宣布µ子磁矩的测量结果与粒子物理“标准模型”理论存在偏差，当时的置信度为4.2标准差。2022年4月，费米国家实验室又在《科学》杂志上报道了W玻色子质量的实验结果，以7个标准差的超高精度证明W玻色子的质量测量值明显偏离其理论预测值。

该结果发表后立刻在学术界引起轰动。很多学者预测这有可能对现有粒子物理的标准模型和希格斯机制提出挑战，甚至预示着新物理理论的诞生。希格斯机制是用于解释包括W玻色子在内的所有基本粒子质量起源的理论，由英国的彼得·希格斯和比利时的弗朗索瓦·恩格勒等物理学家提出[1-3]，所预测的“希格斯粒子”最终于2012年在欧洲核子研究中心被发现，标准模型至此完美收官。希格斯和恩格勒也因此获得了2013年的诺贝尔物理学奖[4]。近年来，一次又一次的偏离理论值的实验结果被报道出来，使人们再一次将目光聚焦在标准模型的 “封碑之作”——希格斯机制上。

01基本粒子的质量起源

何谓“希格斯机制”？简言之，基本粒子，如规范玻色子 (W、Z玻色子等) 和费米子 (夸克、电子等)，与希格斯场发生耦合，从而获得质量，这一过程的作用机制即称为“希格斯机制”。

根据标准模型理论，宇宙中充满了希格斯场，在希格斯机制的作用下发生了自发对称性破缺，进而使基本粒子获得了质量。所谓的场，可以看作是充满整个宇宙的“量”，在理论上是定义在时空上的函数。如图1所示，将希格斯场比作均匀分散着一大群小鱼的水域。当一条大鱼游进这片水域时，吸引了一群小鱼簇拥在其周围，这势必会减缓其游动的速度。此时，大鱼受到的阻碍作用使其具备了“质量”这一属性。基本粒子在获得质量的同时，希格斯场的振动导致量子化激发 (即量子场的微小振荡)，产生希格斯粒子 (即希格斯玻色子)，其通过自耦合而获得质量。

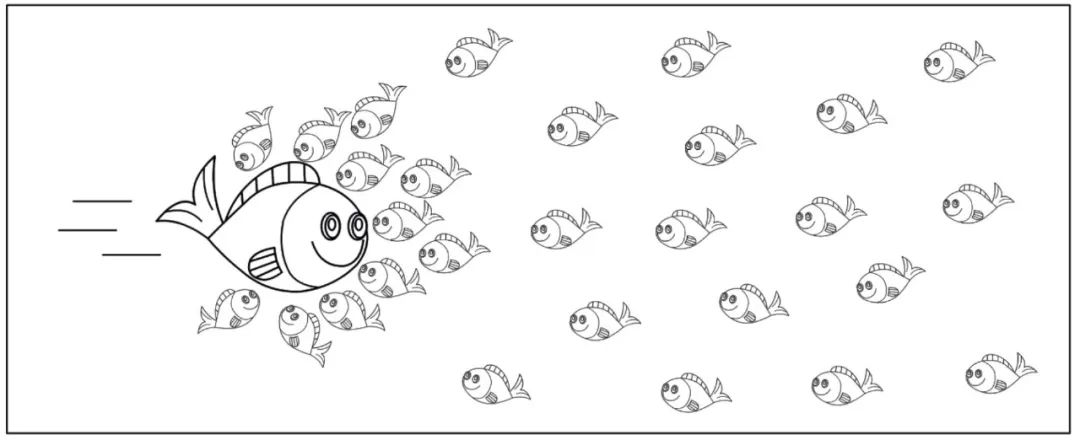
图1 基本粒子通过“希格斯机制”获得质量

02希格斯机制浅析

希格斯机制的提出是数学和物理的又一次巧妙结合。为了解释希格斯机制和W玻色子的质量起源，先从一个多项式函数入手：

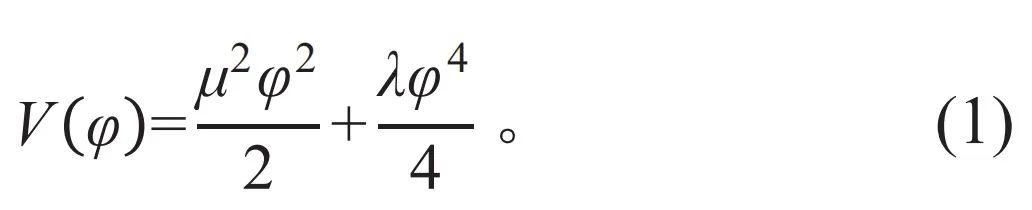
式(1)中，V是φ的函数，包括一个二次项和一个四次项；系数μ和λ是两个常数。将V和φ分别替换为y和x，则式(1)可表示为更一般的形式：

设a与b均为正数，由式(2)作曲线，如图2(a)中红线所示，该曲线在x=0处存在一个极小值；将式(2)的二次项系数设为负值(即a<0)，再次作曲线，如图2(a)中的蓝线所示，该曲线在x=0处存在一个极大值，同时在x=±1处存在两个极小值。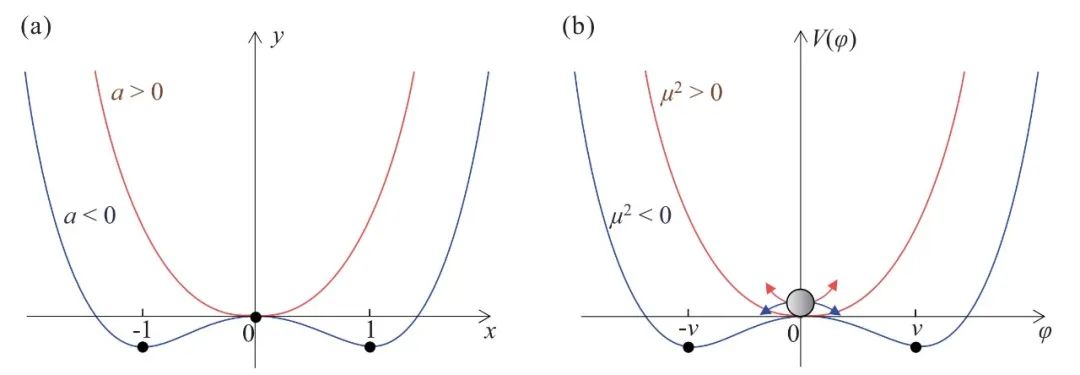
图2  (a)多项式函数曲线(为方便起见，此处设a=±1，b =1)；(b)势能函数曲线

从图2(a)可以看出，当二次项的系数由正值变为负值时，曲线的极值由一个变为三个。由于该多项式函数为偶函数，尽管曲线的形状发生了变化，但相对y轴一直是保持对称的。这个多项式曲线同“希格斯机制”有什么关系呢？

再次回到式(1) 。V(φ)其实来源于一个系统 (即“场”)的势能函数，自变量为φ(φ为实数)，这样的系统称为实标量场。系数µ2为质量项(m2=µ2)，λ表示某种相互作用的强度(λ>0)，µ2和λ共同决定了V(φ)的取值和曲线形状。下面从式(1)出发介绍希格斯机制[5]。

根据被主流物理学界认可的“宇宙大爆炸”理论，宇宙在形成之初处于高能状态，此时µ2>0，势能曲线如图2(b)中的红线所示，在φ=0处有极小值。极小值所处的状态称为该系统的 “真空态”。φ在真空态附近“振动”时会产生 “激发态”。对于一个场来说，激发态的出现就意味着一个新粒子的产生。由µ2>0可知，粒子的质量m有实数解。随着宇宙的降温，系统的能量降低，µ2<0 ，V(φ)演变为图2(b)中的蓝色曲线。此时，势能在φ=0处存在极大值，而在φ=±v处出现两个对称的极小值。根据最小化条件∂V/∂φ=φ(μ2+λφ2)=0求解可得：

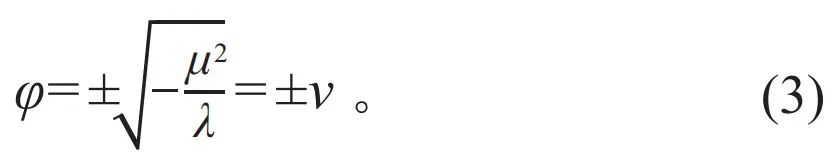
此时存在两个新的真空态：φ=±v(对应的势能极小值为Vmin=-λv4/4)。需要注意的是，因为零点的状态发生了变化，此时m2=μ2<0，即粒子的质量m为虚数，这在真实的物理世界中是不允许存在的。为了解决这个问题，系统会“离开” 零点，自发地选择其中一个真空态，即发生所谓的“自发对称性破缺”，再在新的真空态附近激发新粒子。

假设系统选择φ=v这个点作为新的真空态，需要建立一个新的坐标系，并以该点为零点。由此引入一个新的标量场σ，使得σ=φ-v，将坐标平移变换 (图3(a)) ，得到新的势能函数V(σ)：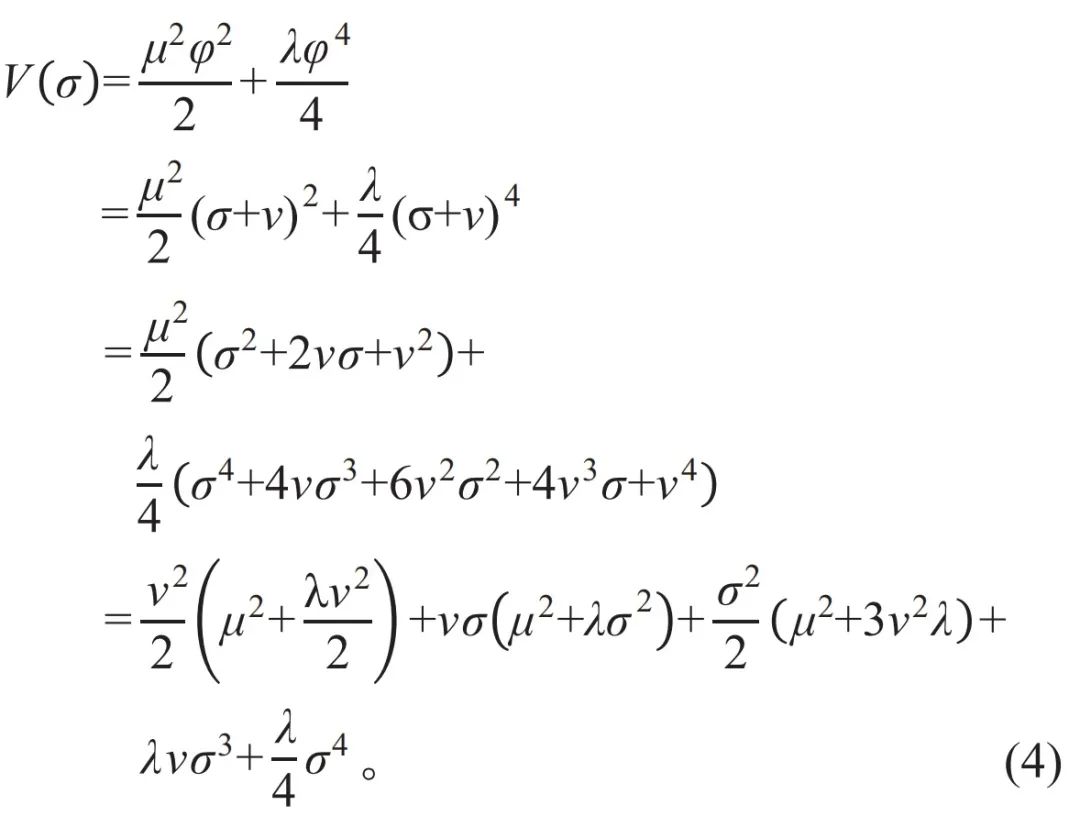

由式(3)可知，μ2=-λv2，代入式(4)可消除其中的一次项，进一步化简后可得：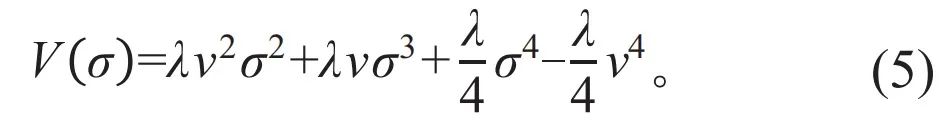
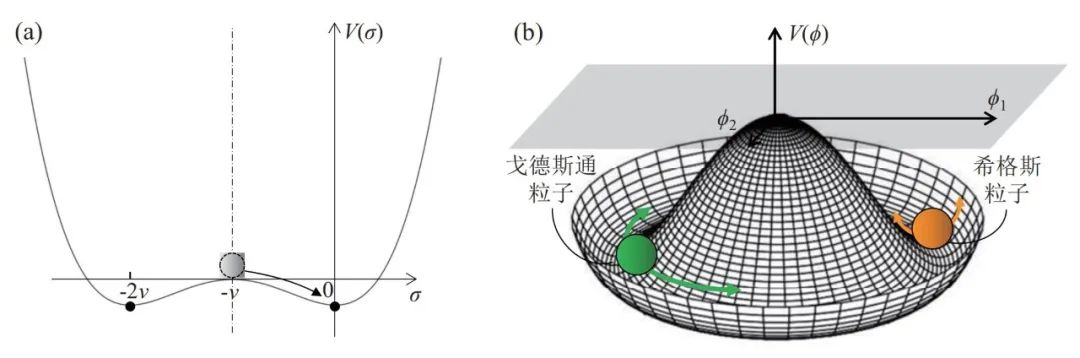图3  (a)对称性破缺后的势能函数曲线； (b)复标量场的势能面

式(5)中的二次项(λv2σ2)系数为正值，质量项m2=2λv2=-2μ2，说明粒子的质量为实数，且m2>|μ2|，表明新标量场σ的相互作用比原来的场φ更强。此外，三次项的出现也说明确实发生了自发对称性破缺，系统最终只能选择一个确定的真空态(φ=v或φ=-v)。这意味着描述我们这个世界的基本法则是“对称”的，但真实世界的选择是 “破缺”的。

进一步将φ从实数扩展到复数，就可以建立一个复标量场ϕ=ϕ1+iϕ2，将系统从一维升级到二维，对应的势能函数V(ϕ)如下：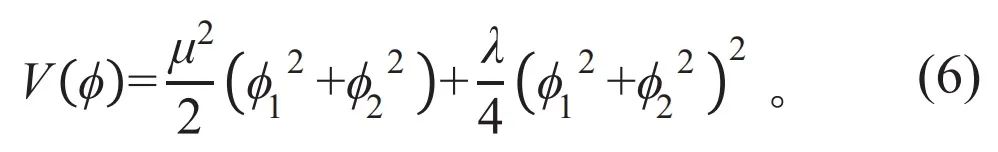

V(ϕ)不再是曲线，而是如图3(b)所示的曲面。在这个类似“墨西哥帽”的势能曲面中，真空态形成了一个半径为v的圆周。从图中可以看出，在这个二维系统中，存在两类粒子：一类粒子以半径v做圆周运动，但沿径向没有位移，永远处于真空态，因此其质量为零，称为“戈德斯通粒子”；另一类粒子在真空态附近沿径向来回 “振动”，质量不为零，即为“希格斯粒子”。这个复标量场称为“希格斯场”，遍布于整个宇宙中，可以同其他基本粒子发生相互作用。希格斯粒子的自旋为零，不带电荷和色荷，且极不稳定 (平均寿命为1.56×10-22 s)，生成后会立刻衰变为其他粒子。

由弱相互作用规范对称性产生的四种无质量的规范玻色子[6]，其中一个继续保持无质量——即光子，另外三个与希格斯场耦合，产生W和Z玻色子，即W+、W-、Z0三个有质量的玻色子。而最初无质量的费米子 (如夸克和电子) 通过与希格斯场发生汤川耦合，从而获得质量。胶子同光子一样，因为不与希格斯场发生相互作用，其质量也为零 (质量为零的粒子以光速运动)。

03希格斯机制与对称性破缺

对称性是物理学中的一个基本概念，表示某个物理系统在进行某种操作或变换后，其某些性质保持不变[6]。“对称性破缺”指原本存在的某种对称性在某些条件下不再保持。而“自发对称性破缺”是指系统的哈密顿量 (或拉格朗日量) 具有某种对称性，但系统的基态 (最低能量状态) 不再保持这种对称性[7]。这意味着在无外界干预的情况下，系统会自发选择一个特定的状态，从而破坏了原有的对称性。所以，自发对称性破缺就是某种确定性从概率的对称性中随机显现出来而形成不对称性的过程，使开放的 (或未知的) 未来变成了确定的“过去”。

对称性破缺是众多物理现象 (如相变、铁磁性、铁电性和超导) 的核心。朗道最早提出了一种基于对称性破缺的相变理论。在相变过程中，无序相对称性高，有序相对称性低。自发对称性破缺就是相结构自发从无序到有序的变化过程。例如，水蒸气凝结为液态水再凝固为冰，就是对称性降低的过程。当某一材料从顺磁体转变为铁磁体时，其对称性发生破缺，即选择了一个特定的磁化方向。超导现象是由于电子在低温下形成库珀对，使系统处于无电阻状态。这种现象伴随着规范对称性的自发破缺。具体来说，超导体中的电磁规范发生对称性破缺，导致光子获得了 “有效质量”。当然，这并不意味着光子真的变 “重”了，而是指电磁波的传播受到了限制，好像具有质量一样 (即迈斯纳效应的起源)。前面提到的戈德斯通粒子源于南部阳一郎和戈德斯通共同提出的“戈德斯通定理”[8]，该定理指出，当一个连续对称性自发破缺时，系统中必然会出现一个无质量的玻色子，即戈德斯通玻色子。

04结语

对称性破缺是宇宙运作与万物形成的底层逻辑。希格斯机制中的对称性破缺产生了“质量”这一最基本的属性，而万物众多属性的形成均源于不同的对称性破缺。物理对称性破缺形成了物质的属性，化学对称性破缺促成了结构的演化，细胞对称性破缺推动了生命的进化，信息对称性破缺塑造了世界的互联。希格斯机制的核心思想是“自发对称性破缺”，而对称性破缺除了用于解释基本粒子的质量起源外，在物理、材料、信息、生物、经济等领域都有着重要的应用。

2022年7月，在希格斯粒子发现十周年之际，《自然》杂志在线汇总了10余篇专题论文纪念这一重大发现[9]。需要指出的是，构成世界万物的复合粒子 (如质子、中子) 的质量中仅有约1%是通过希格斯机制产生的，剩余约99%的质量则源于核子内部夸克的动能和进行强相互作用的胶子的能量。

参考文献

[1] HIGGS P. Spontaneous symmetry without massless bosons [J]. Physical Review, 1966, 145(4): 1156-1163.

[2] ENGLERT F, BROUT R. Broken symmetry and the mass of gauge vector mesons [J]. Physical Review Letters, 1964, 13(9): 321-323.

[3] GURALNIK G, HAGEN C R, KIBBLE T W B. Global conservation laws and massless particles [J]. Physical Review Letters, 1964, 13(20): 585-587.

[4] 刘建北, 刘衍文, 赵政国. 2013年诺贝尔物理学奖解读——希格斯机制的发明与希格斯粒子的发现[J]. 科学中国人, 2014, 259(4): 8-13.

[5] BEDNYAKOV V A, GIOKARIS N D, BEDNYAKOV A V. On the Higgs mass generation mechanism in the Standard Model [J]. Physics of Particles and Nuclei, 2008, 39: 13-36.

[6] 朱宏伟. 规范场纲领[J]. 自然杂志, 2023, 45(4): 303-307.

[7] BEEKMAN A J, RADEMAKER L, VAN WEZEL J. An introduction to spontaneous symmetry breaking [J]. SciPost Physics Lecture Notes, 2019, 11: 1-140. DOI:10.21468/SciPostPhysLectNotes.11.

[8] NAMBU Y. Nobel Lecture: Spontaneous symmetry breaking in particle physics: A case of cross fertilization [J]. Reviews of Modern Physics, 2009, 81(3): 1015.

[9] REICHERT S, LEVI F, GEORGESCU I. The Higgs boson discovery turns ten [EB/OL].(2022-07-04)[2023-09-10]. https://www.nature.com/collections/gbfhieacie.

本文经授权转载自微信公众号“自然撷英”。